2. 中国科学院噪声与振动重点实验室(声学研究所), 北京 100190;
3. 中国科学技术大学 中国科学院材料力学行为和设计重点实验窒, 合肥 230027;
4. 北京石油化工学院 机械工程学院, 北京 102671
2. Key Laboratory of Noise and Vibration Research, Institute of Acoustics, Chinese Academy of Sciences, Beijing 100190, China;
3. CAS Key Laboratory for Mechanical Behavior and Design of Materials, University of Science and Technology of China, Hefei 230027, China;
4. School of Mechanical Engineering, Beijing Institute of Petrochemical Technology, Beijing 102671, China
地壳岩石实际上是极典型的非均匀的多孔材料,是极具复杂性和分散性的高度多组分的介质.组成岩石的矿物颗粒本身还包含颗粒晶体的缺陷、颗粒间的接触、微裂纹、孔洞等,它们之间由胶结物粘结而成为岩石材料.然而这种多孔材料中赋存有各种流体(包括液体和气体),所以岩石材料实际上是一种具有黏弹性特性的黏弹性材料[1].岩石内部结构构造十分复杂,受到载荷作用时,表现出强烈的非线性特征.由于岩石特殊的微细观结构,这种非线性不同于一般的非线性弹性材料,还包括滞后和弛豫[1-6].对岩石施加周期性载荷时,其表现出来的非线性弹性关系就体现在应变滞后于应力一个相位[5].内耗或衰减技术主要用于固体的缺陷与结构的研究,由于其实验技术上的限制,未能对液体存在时引起的能量损耗进行研究[7].岩石中所储存的流体是地球各层间的质量、能量和信息传递的载体.近年来对岩石中包含的液体引起的岩石非线性研究越来越受到重视,研究岩石中的液体引起的弛豫衰减的影响既具有挑战性又具有实际意义,令地学研究者十分感兴趣[8-11].可以认为:在我们对全饱和砂岩所做的实验中,纹间流动是主要的衰减机制.当然,大家公认还需要做相当多的理论工作来论证这个看法[12].为此Daoying Xi等[13-15]还进行了弛豫衰减的理论模型研究.
实验室研究对理解弹性波在特殊岩石中传播的物理机制是非常重要的;如果了解了物理机制,恰当的理论应用就有根据,并且这种结合(实验室研究的物理机制与理论的结合)有助于我们加强理解所要解释的现象[16].Vo-Thanh[17]研究了饱和砂岩中流体黏度对波的衰减和速度的影响.Batzle等[18]通过实验求出了流体流度改变而引起的速度变化. Tutnucu等[17]对多孔隙颗粒状沉积岩在单轴循环应力作用下进行了实验研究,得出应力- 应变滞后曲线的特征与施加载荷的频率、应变振幅以及岩石的饱和流体特性等因素有关.席道瑛等[11]对砂岩、 大理岩进行了循环加载实验,获得不同饱和液体具有不同的滞回曲线特征,反映了饱和岩石特有的非线性力学行为.Zinszner等[19]和Abeele[8]以及席道瑛等[20-22]通过大量实验研究获得砂岩和大理岩的非线性特征(波速衰减)比线性特征更依赖于液体的存在.岩石内部的胶结系统对温度、孔隙流体的属性和应力是十分敏感的.因此,正是岩石的胶结系统的响应使其具有非线性和滞后性.岩石胶结系统中的流体对非线性响应的贡献特别显著,但是,胶结系统以及孔隙流体究竟是如何影响非线性响应的,目前还不十分清楚.为了揭示这些关系,特采用Metravib 热机械分析仪对饱和岩石进行正弦波加载实验,借衰减或内耗对固体材料内部缺陷和结构特敏感的特点,试图从衰减机理方面来探索这个问题.另外,衰减特性比波速对介质的内部结构变化更为敏感,而我们感兴趣的衰减正是介质的内在成因的衰减.衰减随温度升高而减小,在20~100 ℃之间衰减变化达5 倍,这种衰减减小比速度减小的程度大得多[23].所以,在波速与衰减研究中,衰减对地震波的反映比波速灵敏得多[24],因此,衰减的研究对地球物理勘探具有特殊的意义,衰减与油气储存关系的研究也就成了热门的研究课题.
2 实验方法技术采用四川彭山砂岩和自贡长石砂岩,分别加工成直径为9.4mm 长度为50mm 的圆柱形样品;样品两端面平行度<0.02mm.两种岩样各为12 块,样品的饱和处理见文献[5].实验前对样品的孔隙度、密度、渗透率进行了测试.
本次实验采用从法国引进的DMA450 Metravib热机械分析仪.最大力值可达450N 的动态力学分析,频率为10-5 ~103Hz,温度范围为-150~600 ℃.将处理好的样品置于Metravib 试验机的测试平台中心,用704 胶将样品两端面固定在上下压板上.将下压板固定不动,其上压板对岩石样品上端面施加一已知振幅和频率(避开系统的共振频率)的正弦波应力(σ(t)),对样品进行单轴循环加载.用Metravib热机械分析仪直接测量施加的温度、力、砂岩的虚模量Ei、实模量Er 和滞后角(或称耗散角)δ .这种动态力学测试分析仪主要用于材料力学性质及微观机理的研究,研究材料在交变载荷下的应变响应.通过测量应变落后于应力的滞后角(δ)推出材料的能量耗散值,并用衰减Q-1=tanδ 表征其随频率或温度的变化,而这种响应与材料微观结构有密切关系,通过衰减温度谱及频率谱与材料微观结构相关性的研究,可以分析材料在各种条件下的微观结构变化以及与其宏观性能的联系,为材料研究提供更丰富的信息.我们知道固体按其性质可分为两类:一是非结构敏感性的,如弹性模量、 密度、热容量等.对同一种材料的不同样品测量结果差不多.另一类是结构敏感性的,如屈服强度、断裂强度等,对同一种材料的不同样品测量结果差别很大.结构敏感性取决于其中的缺陷分布与运动等具体情况;而内耗或衰减测试技术正是研究和揭示晶体缺陷的一种细致的实验方法,内耗或衰减与缺陷之间有着极为密切而又敏感的关系.岩石是一种内部结构极为复杂、缺陷广布的材料,用内耗或衰减的实验方法来研究岩石的结构敏感性应为一种十分有效的方法.
本实验选择力作为控制参数,选择正弦波的频率为1~400Hz,分别进行温度谱和频率谱试验.实验时固定静载为100N,正弦波动载荷恒为60N,将总载荷控制在屈服点以下.升温速率为1 ℃/min. 以此研究饱和岩石的衰减、模量和弹性波速度对温度和频率的响应.温度控制的稳定度为±0.1 ℃;耗散因子的分辨率为10-5;频率的分辨率为0.01%; 力的分辨率为0.000024N.
3 实验结果及机理探索图 1为泵油饱和彭山砂岩(孔隙度为16.08%)的衰减和lnf-1000/T关系.由图 1a可见随频率增高,峰逐渐变宽,峰高也随之降低,峰的对称性变差,这样宽缓的不对称衰减温度峰,存在一定的分布宽度,它已不是一个单一的Debye峰.由图 1可见,当频率为50Hz时,衰减峰的峰位在16 ℃左右.当频率升到100Hz时,峰位向高温方向移到了23 ℃附近;当频率提高到200 Hz时,峰位已向高温方向移到了34℃左右;当频率再提高到300Hz时,峰位已向高温方向移到了40 ℃左右.可见,泵油饱和彭山砂岩随频率提高,衰减峰峰位向高温方向移动,符合热激活弛豫规律和Arrhenius关系.
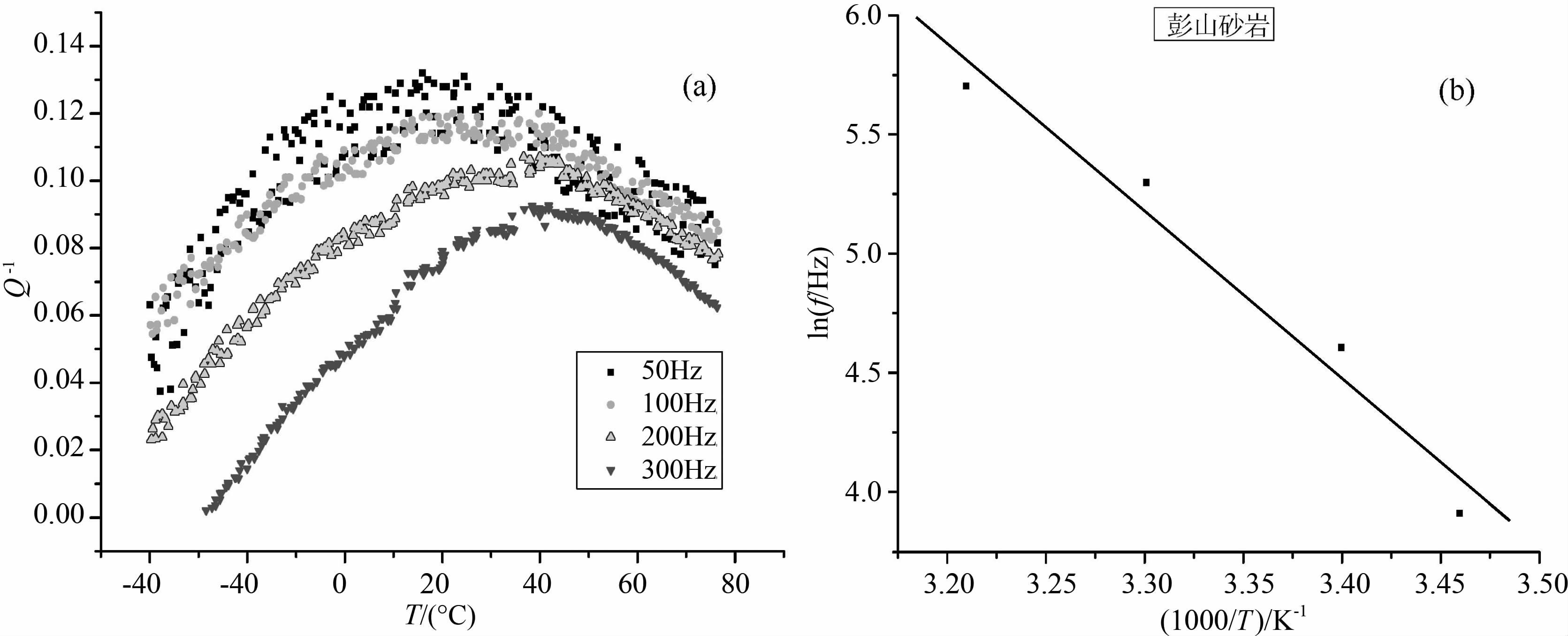
|
图 1 泵油饱和彭山砂岩(孔隙度为16.08%)的衰减特性 (a)衰减温度谱;(b) lnf-1000/T关系. Fig. 1 Attenuation properties for pump-oil saturated Pengshan sandstone (16.08% porosity) (a) Attenuation vs.temperature; (b) Relationship of lnf to 1000/T. |
由于激活能H是描述弛豫过程的一个极为重要的参数,它与τ0 一起能直接反映出弛豫的微观机理.因此我们可通过弛豫时间τ 和温度T遵循的Arrhenius方程[25]:
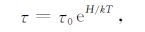
|
(1) |
式中τ0 是弛豫时间,H是激活能,k是玻尔兹曼常数,T是绝对温度.该方程直接把饱和岩石的黏弹行为与具有一定激活能的分子速度过程联系起来了. 只有当ωτ 为中间值时,应变弛豫跟不上应力的变化,产生一滞后角,才会引起衰减.
当ωτ =1时,衰减达到极大值.我们通过这一关系求出激活能:
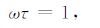
|
(2) |
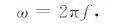
|
(3) |
将(1) 、(3) 代入(2) 式可得:
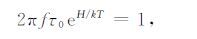
|
(4) |
将式(4) 取对数,得
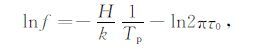
|
(5) |
由式(5) 可以看出,lnf与1/TP 成线性关系,其中TP 为峰值点的开氏温度.因此可以通过改变频率的方法来求取激活能.设在f1 频率下测到的衰减峰峰温为T1,f2 频率下衰减峰峰温为T2,当频率由f1 变到f2 时峰温由T1 变到T2:
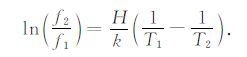
|
(6) |
根据Arrhenius关系可拟合得到lnf和弛豫衰减峰的峰温的倒数(1000/T)成直线关系(见图 1b). 图 1b 是与图 1a相对应的弛豫衰减峰的峰温与频率的Arrhenius关系(lnf-1000/T)图.图 1b的泵油饱和彭山砂岩(孔隙度为16.08%)的拟合关系为
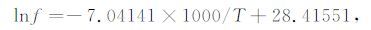
|
(7) |
拟合直线的截距为弛豫时间τ0,直线的斜率为激活能(原子跃迁所需的能量)H.由此可以得到泵油饱和彭山砂岩(孔隙度为16.08%)弛豫衰减峰的激活能H约为0.607e V,弛豫时间τ0 约为7.26×10-15s.
我们知道,岩石尤其是饱和岩石更是一种多晶、 多相的固体,这里以图 2 的长石砂岩的正交偏光显微图片为例进行说明.其中的矿物晶体主要是长石(55%)、石英(10%~15%)、岩屑(5%~10%)、胶结物(20%~30%)等矿物晶体,以粘土质胶结为主.可见砂岩是一种多晶的固体材料,是由许多方位一致性质不同的小晶粒组合而成(见正交偏光显微镜下的长石砂岩微细观结构图片).因此颗粒可以相互摩擦滑动产生颗粒边界的弛豫衰减[23];根据饱和岩石中内部结构的复杂、缺陷广布的特性分析,饱和岩石中的矿物晶体颗粒之间的晶界等以及饱和液体与岩石骨架之间的相界都可以产生这种类型的弛豫衰减.由上面介绍的弛豫衰减峰的特征结合饱和岩石中的上述各种缺陷、相界等等会导致多重弛豫,才使弛豫衰减峰变宽,分布参数增大.

|
图 2 正父偏光显微镜下的长石砂岩微细观结构图片(5 × 10) ()长石砂岩;(b)长石石英砂岩. Fig. 2 Meso-structure picture of feldspar sandstone by orthogonal polarizing microscope (5×10) (a) Feldspar sandstone; (b) Feldspar quartz sandstone. |
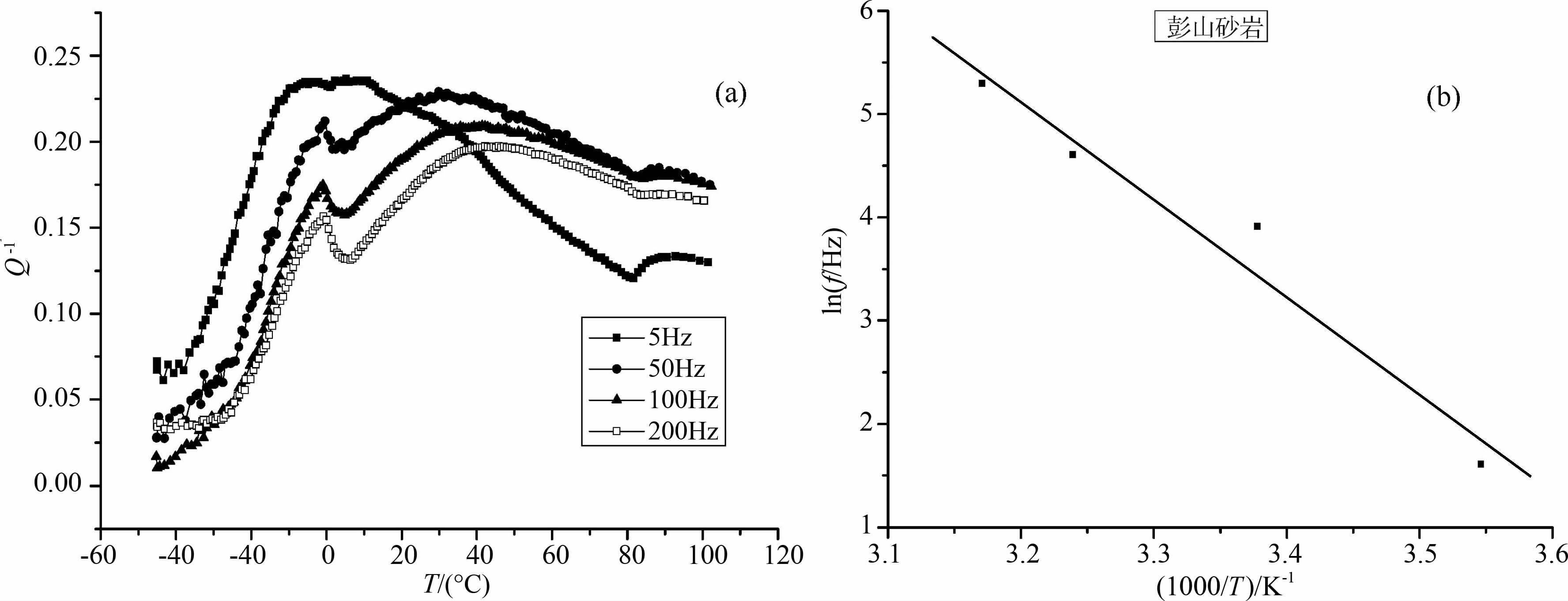
图 3为泵油饱和彭山砂岩(孔隙度为17.07%) 的衰减和lnf-1000/T关系.由图 3a不难看出,该衰减峰的特征类似于图 1a,衰减峰在0 ℃左右的波动是由静载波动引起.当频率为5 Hz时,衰减峰的峰位在5 ℃左右.当频率升到50Hz时,衰减峰峰位已向高温方向移到了31℃,当频率提高到100Hz时,衰减峰峰位已向高温方向移到了40℃,当频率最后提高到200 Hz时,衰减峰峰位已移到了46 ℃.可见,衰减峰峰位随频率提高向高温方向移动的规律与图 1是一致的,也符合热激活弛豫规律和Arrhenius关系.其产生该衰减峰的机理也与之类似.
|
图 3 泵油饱和彭山砂岩(孔隙度为17.07%)的衰减特性()衰减温度谱;(b) lnf-1000/T关系. Fig. 3 Attenuation properties for pump-oil saturated Pengshan sandstone (17.07% porosity) (a) Attenuation vs.temperature; (b) Relationship of lnf to 1000/T. |
图 3b是与图 3a相对应的弛豫衰减峰的峰温与频率的Arrhenius关系(lnf-1000/T)图.用图 1b类似的方法可求得图 3b的泵油饱和彭山砂岩(孔隙度为17.07%)弛豫衰减峰的峰温与频率的拟合关系为

|
(8) |
由此可求得泵油饱和彭山砂岩(孔隙度为17.07%)的弛豫衰减峰的激活能H约为0.815e V,弛豫时间τ0 约为7.06×10-17s.
下面通过激活能和跃迁频率进一步分析引起该弛豫衰减峰的机理.两种泵油饱和彭山砂岩的弛豫衰减峰的激活能H(0.607e V;0.815e V)在同一量级,弛豫时间τ0(7.26×10-15s ;7.06×10-17s)差两个量级,这个值比点缺陷跳跃的典型弛豫时间(10-12~10-14)值要小得多[26],它们也是处在电子的激活能和跃迁频率之间.该值的倒数代表了原子的振动频率,此振动频率说明参与沿着晶粒间界扩散的只可能是孔隙中的饱和液体原子或电子,这一液体分子中的原子断开,造成振动频率增高,因为固体原子的振动频率与其相比要低几个量级.振动频率增高,弛豫的时间就自然减小.两种彭山砂岩的组成成分、内部结构相差不大,其孔隙度的差异约为1%,导致激活能和弛豫时间有所不同.不难得出,随着孔隙度增大,激活能和衰减强度有所增大,弛豫时间缩短.
图 4为泵油饱和长石砂岩(孔隙度为11.1%) 的衰减温度谱和lnf-1000/T关系.由图 4a可见,当频率较低时,是一个峰宽相对较窄、峰值明显而且极为不对称的衰减峰.当频率为5 Hz时,衰减峰的峰位在-14 ℃左右,当频率继续提高到10Hz时,衰减峰峰位已向高温方向移到了-5 ℃,当频率最后提高到400Hz时,相应的衰减峰峰位由-5 ℃已向高温方向移到了约39 ℃.可见,衰减峰峰位随频率提高向高温方向移动的规律与上述两种泵油饱和彭山砂岩一致,也符合热激活弛豫规律和Arrhenius关系.

|
图 4 泵油饱和长石砂岩(孔隙度为11.1%)的衰减特性 (a)衰减温度谱;(b) lnf-1000/T关系. Fig. 4 Attenuation properties for pump-oil saturated Zigong arkoses(11.1% porosity) (a) Attenuation vs.temperature; (b) Relationship of lnf to 1000/T. |
图 4b是与图 4a相对应的弛豫衰减峰的峰温与频率的Arrhenius关系(lnf-1000/T)图.用上述类似的方法可以求得图 4b的泵油饱和长石砂岩(孔隙度为11.1%)弛豫衰减峰峰温与频率的拟合关系为
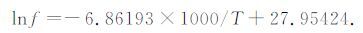
|
(9) |
由此可求得泵油饱和长石砂岩的弛豫衰减峰的激活能H约为0.59e V,弛豫时间τ0 约为1.15×10-13s.
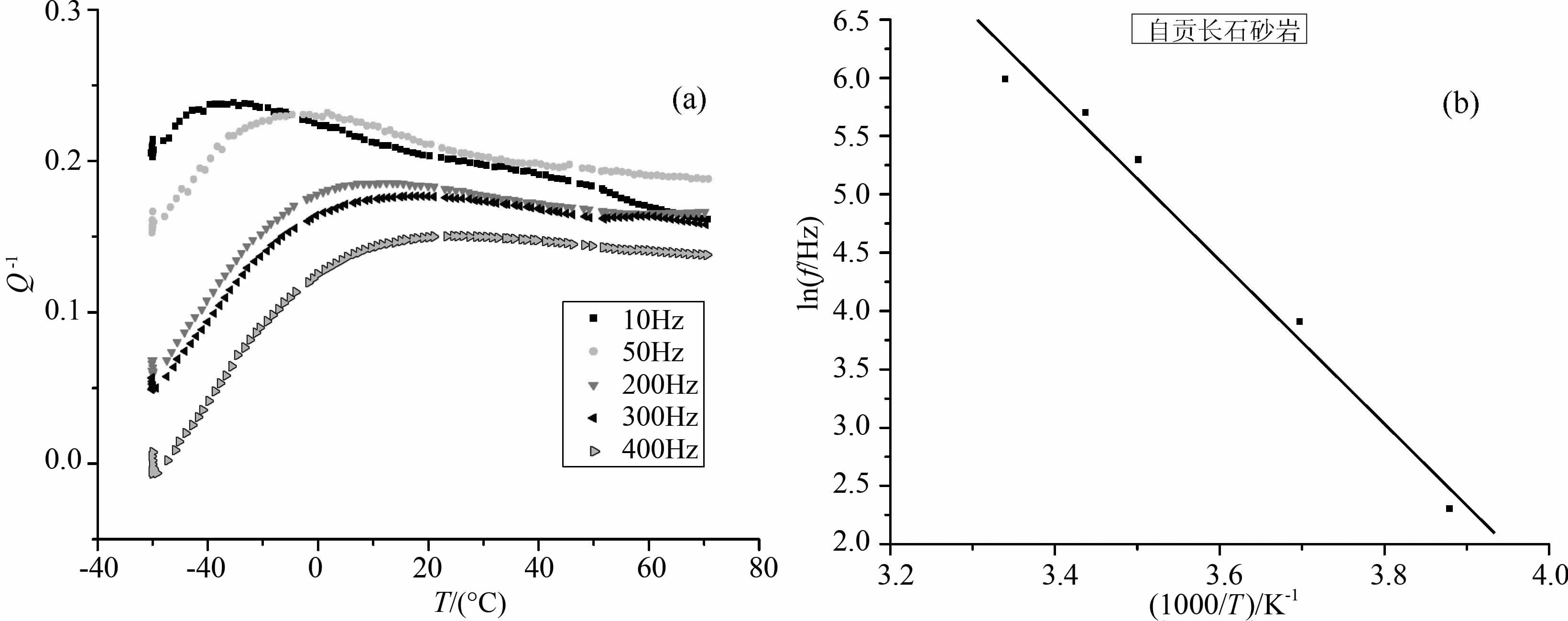
图 5为泵油饱和长石砂岩(孔隙度为12.84%) 的衰减温度谱和lnf-1000/T关系.由图 5a不难看出,当频率为10Hz时,衰减峰的峰位在-15 ℃ 左右;当频率升到50Hz时,衰减峰峰位移到了-4℃.当频率提高到200Hz时,衰减峰峰位已向高温方向移到了7 ℃.当频率升到300 Hz时,衰减峰峰位移到了15℃.当频率最后提高到400Hz时,衰减峰峰位也向高温方向移到了22 ℃.可见,衰减峰峰位随频率提高向高温方向移动,也符合热激活弛豫规律.泵油饱和长石砂岩的衰减温度峰与图 4a的弛豫衰减峰有类似的特征,在50 Hz以下的低频时,峰宽较窄,衰减峰值较明显,峰的对称性差;随频率提高到50Hz以上,衰减峰的衰减值先随温度升高而增大,达到峰值后再随温度升高缓慢下降或趋于平缓,峰宽明显增大.可见它们也不是单一的弛豫机制引起的,是多重弛豫机制迭加而成.同样根据Arrhenius 关系可拟合得到lnf和峰温的倒数(1000/T)成直线关系(见图 5b).图 5b 是与图 5a相对应的弛豫衰减峰的峰温与频率的Arrhenius关系(lnf-1000/T) 图.用与上述类似的方法可以求得图 5b的泵油饱和长石砂岩(孔隙度为12.84%)弛豫衰减峰峰温与频率的拟合关系为
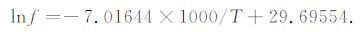
|
(10) |
由此可求得泵油饱和长石砂岩的弛豫衰减峰的激活能H约为0.605e V,弛豫时间τ0 约为2.02×10-14s.
|
图 5 泵油饱和长石砂岩(孔隙度为12.84%)的衰减温度谱 (a)和lnf-1000/T关系(b) Fig. 5 Attenuation properties for pump-oil saturated Zigong arkoses (12.84% porosity) (a) Attenuation vs.temperature; (b) Relationship of lnf to 1000/T. |
由图 4、5a可见,其衰减峰出现在较低温度,在低频时峰宽较窄,衰减峰值较明显,衰减对温度较敏感,峰的对称性差,随着频率的提高衰减值随温度升高先增大,后趋于平缓,峰宽明显增大.也就是说随着温度的升高,温度变化对衰减的影响变得越来越小.由此可得,泵油饱和长石砂岩除热弛豫过程对衰减的贡献外,还存在其他与温度或频率有关的机制在起作用,如阻尼衰减.低频下热弛豫型衰减机制起主导作用,随着频率增大,阻尼弛豫型机制起的作用在逐渐增大,它与热弛豫型衰减机制对衰减起互补作用,导致衰减在高温时基本处于恒定.在流体饱和砂岩中,衰减对饱和液体的黏滞性高度敏感,可观察到一两个衰减峰值[27].由于孔隙液体的黏滞系数是随温度变化的,孔隙液体在周期性应力作用下与孔隙界面一起运动,在不同温度时可以产生不同的能量损耗[24].一般来说,在我们这次实验所使用的正弦波交变应力作用下,在多种矿物晶体胶结而成的长石砂岩中,晶界这一缺陷的运动必将引起衰减峰. 频率增加时,峰向高温移动,是一个线性弛豫型弛豫衰减峰.这种多晶材料沿晶粒间界的黏滞性滑动所引起的这一弛豫型衰减峰,其弛豫过程还会受到晶界上原子扩散的控制.下面通过激活能和跃迁频率进一步分析引起该弛豫衰减峰的微观机理.
两种泵油饱和长石砂岩的弛豫衰减峰的激活能H(0.59e V;0.605e V)在同一量级,弛豫时间τ0(1.15×10-13s;2.02×10-14s)相差一个量级.岩石这种多晶的固体材料,由许多性质不同的矿物小晶体胶结而成.在岩石这种多晶的固体材料的晶体中,原子虽然相对地稳定,但在温度逐渐升高的情况下,它们也可以通过所谓“扩散"的方式在晶体中移动.扩散的过程与晶体的微观缺陷有密切关系,晶粒间界是岩石矿物晶体的主要缺陷,一般的晶粒间界附近几层原子是按晶格排列但有较大畸变,故此原子可以比较容易沿着晶粒间界扩散.所以外界的原子可以渗入并分布于晶粒间界处,内部的杂质原子或夹杂物也往往容易集中在晶粒间界处,这些都可以使晶粒间界具有复杂的动性和物理力学性质,并产生各种影响[28].而弛豫时间τ0(1.15×10-13s;2.02 ×10-14s)的值,正是点缺陷跳跃的典型弛豫时间[26],也是原子振动的弛豫时间(10-12~10-14s); 泵油饱和长石砂岩的激活能稍偏小,说明产生该弛豫衰减峰相对容易一些;并说明参与沿着晶粒间界扩散的是原子.两种长石砂岩的组成成分、内部结构都差不多,孔隙度差1.5%左右(11.1%;12.84%),从它们的激活能和跃迁频率数值来看,与泵油饱和彭山砂岩一样似乎也存在着随孔隙度增大,激活能和衰减强度增大,弛豫时间减小的趋势.
4 结论和讨论由于衰减对地震波的反映比波速更敏感,因此,研究衰减及其机理对地球物理尤其是地球物理勘探具有特殊意义.本文采用从法国引进的热机械分析仪以正弦波加载方式,首次对四种不同孔隙度的泵油饱和彭山和自贡长石砂岩的滞弹性衰减进行了实验研究,并根据饱和砂岩弛豫衰减峰的特征探索了衰减的机理,自然而然地将弛豫衰减的宏观现象与饱和砂岩的微细观结构紧密地联在了一起.
我们在5~400 Hz的频率,-50~100 ℃ 温度范围的实验中,获得了泵油饱和彭山砂岩和长石砂岩的衰减峰的峰位随振动频率提高向高温方向移动的弛豫规律,符合Arrhenius关系.以此取得了产生弛豫衰减峰的激活能和振动频率.这一结果与10Hz以下的共振实验的驻波取得的弛豫规律相符[1].证实了弛豫机制在地壳饱和岩石中可能是普遍存在的;这给地球物理勘探的资料解释和岩石物理理论模型的研究[14-15]提供了实验基础,并以取得的新的机理去寻求新的思路.
获得两种泵油饱和彭山砂岩和两种泵油饱和长石砂岩的弛豫衰减的激活能和与电子、原子的弛豫时间.由此分析可见,它们的激活能H都在同一量级,弛豫时间τ0 却各有不同.泵油饱和彭山砂岩的激活能和弛豫时间是处在原子和电子的激活能和弛豫时间之间;泵油饱和长石砂岩的弛豫衰减的激活能和弛豫时间是处在原子的激活能和弛豫时间之间.在岩石的矿物晶体中,原子虽然处于相对稳定状态,当温度不断升高时,原子也会通过扩散在晶体中移动.而且原子比较容易沿着晶粒间界这种缺陷扩散.所以外界的原子和内部的杂质原子或夹杂物都集中在晶粒间界处,导致晶粒间界具有复杂的性质,并影响材料的宏观性能.由此可见,在岩石的缺陷处参与沿着晶粒间界扩散的是原子和电子.不难得出,随着孔隙度增大,激活能和衰减强度均有所增大,弛豫时间减小.
在这次实验所使用的正弦波交变应力作用下,在多种矿物晶体胶结而成的砂岩中,尤其是饱和岩石更是一种多晶、多相的固体,因此颗粒可以相互摩擦滑动产生颗粒边界的弛豫,而且多晶材料的晶界沿晶粒间界的黏滞性滑动也能引起弛豫型衰减峰,其弛豫过程还受晶界上原子或电子扩散所控制.根据上述弛豫衰减峰的特征,结合饱和岩石内部结构的复杂、缺陷广布的特征分析,饱和岩石中的上述缺陷及晶界等以及饱和液体与岩石骨架之间都可以产生这种类型的弛豫衰减峰.饱和岩石这种多晶多相的聚集体中的矿物是天然产出的无机结晶化合物. 这种无机结晶化合物不同于有机的金属材料,产生弛豫衰减是不难的,但引起衰减的因素就较多.不过La2NiO4+δ 无机结晶化合物像金属材料一样,成分和结构都比较单一.在温度为250K 附近也发现因不同含氧量引起的弛豫衰减峰[29].由于La2NiO4+δ成分结构的单一性,可以给出引起弛豫衰减峰的明确的机理,而因岩石成分和结构的复杂性导致对弛豫衰减机理解释的不唯一性.正是由于饱和岩石中的各种缺陷、相界等等在交变应力作用下产生不同的弛豫,才会导致多重弛豫,使弛豫衰减峰变宽,分布参数增大.当然,也有可能还存在别的衰减机制. 比如泵油饱和长石砂岩除热弛豫过程对衰减的贡献外,或许还存在其他与温度或频率有关的衰减机制在起作用,如阻尼衰减.
地震波的衰减机制和测量方法技术研究一直处在岩石物理研究的前沿,得到岩石物理研究者的青睐.因为地震资料解释中还存在许多悬而未决的问题,机理的研究为实际地震响应分析和属性反演提供了依据,这些都有助于地震资料的解释;机理的研究更有助于理论模型的改进和发展.可见,我们这一规律性的实验结果给理论模型研究奠定了实验基础,对地震资料的解释具有实用意义.
| [1] | Xi D Y, Liu X Y, Zhang C Y. The frequency (or time)-temperature equivalence of relaxation in saturated rocks. Pure. Appl. Geophys. , 2007, 164(11): 2157-2173. DOI:10.1007/s00024-007-0270-z |
| [2] | Guyer R A, TenCate J, Johnson P. Hysteresis and the dynamic elasticity of consolidated granular materials. Physical Review Letters , 1999, 82(16): 3280-3283. DOI:10.1103/PhysRevLett.82.3280 |
| [3] | Johnson P A, McCall K R. Observation and implications of nonlinear elastic wave response in rock. Geophysical Research Letters , 1994, 21(3): 165-168. DOI:10.1029/93GL03162 |
| [4] | 席道瑛, 陈运平, 陶月赞, 等. 岩石的非线性弹性滞后特征. 岩石力学与工程学报 , 2006, 25(6): 1086–1093. Xi D Y, Chen Y P, Tao Y Z, et al. Nonlinear elastic hysteric characteristics of rocks. Chinese Journal of Rock Mechanics and Engineering (in Chinese) (in Chinese) , 2006, 25(6): 1086-1093. |
| [5] | 席道瑛, 徐松林, 席军, 等. 饱和砂岩的粘弹行为的实验研究. 地球物理学报 , 2011, 54(9): 2302–2308. Xi D Y, Xu S L, Xi J, et al. Experimental research on viscoelastic behavior for saturated rocks. Chinese Journal of Geophysics (in Chinese) (in Chinese) , 2011, 54(9): 2302-2308. |
| [6] | Tutuncu A N, Podio A L, Gregory A R, et al. Nonlinear viscoelastic behavior of sedimentary rock, part II: hysteresis effects and influence of type of fluid on elastic moduli. Geophysics , 1998, 63(1): 195-203. DOI:10.1190/1.1444313 |
| [7] | Nonick A S, Berry B S. An Elastic Relaxation in Crystalline Solida. New York: Academic Press, 1972 : 74 -83. |
| [8] | van den Abeele K E A, Carmeliet J, Johnson P A, et al. Influence of water saturation on the nonlinear elastic mesoscopic response in Earth materials and the implications to the mechanism of nonlinearity. J. Geophys. Res. , 2002, 107(B6): 2121-2131. DOI:10.1029/2001JB000368 |
| [9] | Carmeliet J, van den Abeele K. Mesoscopic approach for modelling the nonlinear hysteretic response of damaged porous media in quasi-static and dynamic loading: Effects of pressure and moisture saturation. Fourth International Conference on Fracture Mechanics of Concrete and Concrete Structures, Cachan, France , 2001, 28: 11-18. |
| [10] | Carmeliet J, Koen E A, van den Abeele. Application of the Preisach-Mayergoyz space model to analyze moisture effects on the nonlinear elastic response of rock. Geophys. Res. Lett. , 2002, 29(7): 1144-1147. DOI:10.1029/2001GL014243 |
| [11] | 席道瑛, 杜赟, 易良坤, 等. 液体对岩石非线性弹性行为的影响. 岩石力学与工程学报 , 2009, 28(4): 687–696. Xi D Y, Du Y, Yi L K. Influence of fluid on nonlinear elastic behavior of rock. Chinese Journal of Rock Mechanics and Engineering (in Chinese) (in Chinese) , 2009, 28(4): 687-696. |
| [12] | Winkler K W, Nur A. Seismic attenuation: Effects of pore fluids and frictional sliding. Geophysics , 1982, 47(1): 1-15. DOI:10.1190/1.1441276 |
| [13] | 席道瑛, 易良坤, 田象燕. Biot理论的唯象修正对S波持性的影响. 地球物理学报 , 2003, 46(6): 814–820. Xi D Y, Yi L K, Tian X Y. Influences of phenomenological modification of biot theory on characteristics of S-wave. Chinese J. Geophys. (in Chinese) (in Chinese) , 2003, 46(6): 814-820. |
| [14] | Xi D Y, Xu S L, Du Y, et al. Wave propagation analysis of porous rocks with thermal activated relaxation mechanism. Journal of Applied Geophysics , 2011, 71(3): 289-303. |
| [15] | 杜赟, 席道瑛, 徐松林, 等. 多孔岩石波传播的热弛豫模型修正. 地球物理学报 , 2009, 52(12): 3051–3060. Du Y, Xi D Y, Xu S L, et al. The modification of thermal relaxation mechanism for wave propagation in porous rocks. Chinese J. Geophys. (in Chinese) (in Chinese) , 2009, 52(12): 3051-3060. |
| [16] | Pennington W D. Seismic Petrophysics: An applied science for reservoir geophysics. The Leading EDGE , 1997, 16(3): 241-244. DOI:10.1190/1.1437608 |
| [17] | Vo-Thanh D. Influence of fluid chemistry on shear wave attenuation and velocity in sedimentary rocks. Geophys. J. Int , 1995, 121(3): 737-749. DOI:10.1111/gji.1995.121.issue-3 |
| [18] | Batzle M, Han D, Castagna J. Attenuation and velocity dispersion at seismic frequencies. Soc. Expl. Geoph., Expanded Abstracts , 1996: 1687-1690. |
| [19] | Tutuncu A N, Podio A L, Gregory A R, et al. Nonlinear viscoelastic behavior of sedimentary rocks, Part I: Effect of frequency and strain amplitude. Geophysics , 1998, 63(1): 189-194. |
| [20] | Zinszner B, Johnson P A, Rasolofosaon P. Influence of change in physical state on elastic nonlinear response in Rock: Effects of Confining Pressure and Saturation. J. Geophys. Res , 1997, 101: 8105-8120. |
| [21] | 席道瑛, 刘斌, 刘卫, 等. 饱和多孔岩石弛豫衰减对时间和温度的依赖性. 地球物理学报 , 2000, 43(6): 873–880. Xi D Y, Liu B, Liu W, et al. The dependence of relaxation attenuation of saturated rock on time and temperature. Chinese J. Geophys. (in Chinese) (in Chinese) , 2000, 43(6): 873-880. DOI:10.1002/cjg2.v43.6 |
| [22] | 席道瑛, 刘斌, 田象燕. 饱和岩石的各向异性及非线性粘弹性响应. 地球物理学报 , 2001, 45(1): 101–111. Xi D Y, Liu B, Tian X Y. Anisotropy and nonlinear viscoelastic behavior of saturated rocks. Chinese J. Geophys. (in Chinese) (in Chinese) , 2001, 45(1): 101-111. |
| [23] | Jones T, Nur A. Velocity and attenuation in sandstone at elevated temperatures and pressures. Geoph. Res. Lett. , 1983, 10(2): 140-143. DOI:10.1029/GL010i002p00140 |
| [24] | 席道瑛, 程经毅, 席军. 饱和砂岩滞弹性弛豫热激活过程机理探讨. 石油地球物理勘探 , 1998, 33(3): 348–354. Xi D Y, Cheng J Y, Xi J. Research on the heating activation mechanism of viscoelastic relaxation in fluid-saturated sandstone. Oil Geophysical Prospecting (in Chinese) (in Chinese) , 1998, 33(3): 348-354. |
| [25] | 沃德IM. 固体高聚物的力学性能. 北京: 科学出版社, 1988 : 164 -167. Ward I M. Mechanical Behavior of Solid Polymers (in Chinese) (in Chinese). Beijing: Scientific Press, 1988 : 164 -167. |
| [26] | 刘卫, 张艳敏, 吴修胜, 等. GdBaCo2O5+δ体系的滞弹性内耗研究. 物理学报 , 2006, 55(11): 5996–6000. Liu W, Zhang Y M, Wu X S, et al. Anelastic relaxation of excess oxygen in GdBaCo2O5+δ system studied by low-frequency internal friction. Acta Physica Sinica (in Chinese) (in Chinese) , 2006, 55(11): 5996-6000. |
| [27] | 布尔贝O T, 库索B, 甄斯纳著. 孔隙介质声学. 北京: 石油工业出版社, 1994 : 148 . Boulbet T, Cousot O, Reissner B. Porous Medium Acoustics (in Chinese) (in Chinese). Beijing: Petroleum Industry Press, 1994 : 148 . |
| [28] | 黄昆编著. 固体物理学. 北京: 人民教育出版社, 1979 : 66 -67. Huang K. Solid Physics (in Chinese) (in Chinese). Beijing: People's Education Press, 1979 : 66 -67. |
| [29] | Zhang H L, Wu X S, Chen C S, et al. Excess oxygen ordering in the La2NiO4+δ system studied by low-frequency internal friction. Physical Review , 2005, 71(6): 064422:1-7. |
 2012, Vol. 55
2012, Vol. 55

