月球重力场是一个综合反映月球内部密度分布的重要位场资料,可对月球的结构构造提供可靠的约束.迄今为止,月球重力场的探测主要是通过测定月球对卫星轨道摄动来解算月球重力场.本文回顾了月球重力场的探测历史,研究了影响月球重力场解算精度的因素,并利用日本公布的采样间隔为60s的SELENE 探月卫星数据,进行月球重力场的解算,取得了很好的结果.
1966年,苏联的Luna10号探测器成为首颗绕月卫星并率先建立了月球重力场.尽管绕月只有56 天,219个探测数据,但却第一次建立了月球重力场[1]. 1966-1967年,覆盖范围为20°S-30°N 的Lunar Orbiter I/II/III轨道探测器在月球正面近月点飞行高度最低达到40km,但这三颗卫星只获得了月球赤道附近地区的轨道探测数据.由于其比Luna10 号平均轨道高度要低,因此在覆盖区内解算出的重力场精度得到了提高.Lunar Orbiter IV 号和V 号探测器还首次获得了一些月球高纬度和两极区域的轨道数据[2],但是其轨道高度为200~6000km,因此在该区域的重力场精度较低.1966-1967 年,Lunar Orbiter系列轨道探测器(Ⅰ~Ⅴ)总共获得了32600个观测数据,较Luna10 号覆盖率有所增多. 1968年Lorell与Sjogren[3]利用Lunar Orbiter系列卫星的探测数据首次建立了8×4 月球球谐系数模型.Micheal与Blackshear[2]又建立了13×13 模型(13阶次),此模型在月球20°S-30°N 范围较8× 4模型有所提高.Apollo15 (1971 年)、16 号(1972 年)的子卫星首次将轨道降低到100km 高度,但是只覆盖了南北纬30°范围以内的地区[4].由于轨道高度较低,因此对于该区域内的重力场解算精度又得到了进一步的提高[5].1980 年,Bills和Ferrari[6]利用Lunar Orbiter I-V 和Apollo15和16号子卫星轨道数据以及Apollo任务中一些激光测距数据建立了16阶次模型.1993年,Konopliv等[7]又将球谐模型提升到了60 阶次(Lun60d 模型).1997 年Clementine的激光高度数据改进了月球重力场的低阶次系数,建立了70阶次GLGM-2(Goddard Lunar Gravity Model)模型[8].1998 年,JPL(喷气推进实验室)对Lun60d进行改进建立了Lun75f(75阶次) 模型.同年,Lunar Prospector进行了100km 低圆极轨的探测,获得了3648853 个数据,其中,在最后的6个月中,还将轨道降低到了30~40km,甚至在某些近月点处高度降低到10km,这大大改进了月球正面重力场的精度.随后,Konopliv等[9]建立了75阶次月球位场模型---LP75D 和LP75G,其中LP75G 比LP75D增加了两个月的轨道数据.随着Lunar Prospector 探测数据量的进一步增加,又建立了100阶次月球位场模型---LP100J和LP100K.后来又建立了165 阶次月球位场模型LP165P.在此基础上又利用改进的算法(即建立单个解算矩阵模型)[10]建立了150 阶次月球位场模型---LP150Q.尽管如此,由于月球的背面总是背对地球,这就导致一直以来都未能获得月球背面的低轨道直接探测数据,这部分约占月球总面积的33%.这就使LP150Q 模型在月球正面重力场的误差为30m Gal,而在月球背面的误差却达到200m Gal,且在位置上还有较大的水平偏移[11].
2007年,日本发射的SELENE(Kaguya)探测器利用中继卫星(RSAT)和主卫星(Main)以及4- way Doppler雷达探测技术首次在100km 轨道高度上探测到了月球背面的重力场信息[12],首次建立了全月球高精度的重力场模型---SGM90d(其计算用的采样间隔为10s[12]).至此,月球重力场才完整,才可用于全月球的重力场研究.当前各国正在进一步提高月球和行星重力场的探测精度.2011 年9 月10 日发射的GRAIL 卫星就是专门为探测高精度月球重力场而设计的.
综上所述,月球卫星重力场探测历史就是从高轨道到低轨道、从部分覆盖到全球覆盖、从低密度采样到高密度采样的探测历程.未来月球重力场探测仍然沿着低轨道、圆极轨、高采样率的路线发展,甚至未来还可能需要地面、超低轨道航天重力观测卫星,以求得更高精度的月球重力场信息.
2 方法与原理卫星轨道动力学原理是利用卫星轨道数据计算月球重力场模型的基础.卫星的运动可以分为无摄运动和有摄运动.无摄运动是卫星运行的一级近似,只受万有引力作用的影响.此时可以建立6 个轨道根数与卫星运动之间的关系(公式(1)).此时的轨道根数是不随时间变化的.
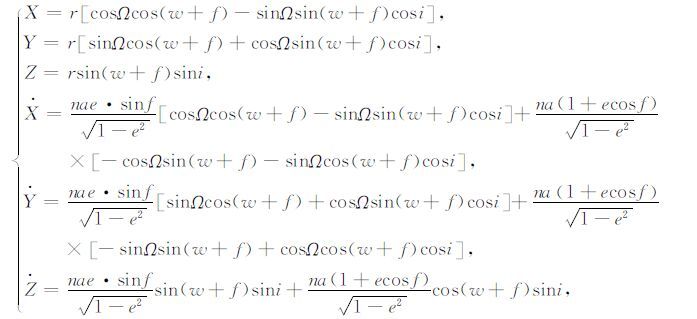
|
(1) |
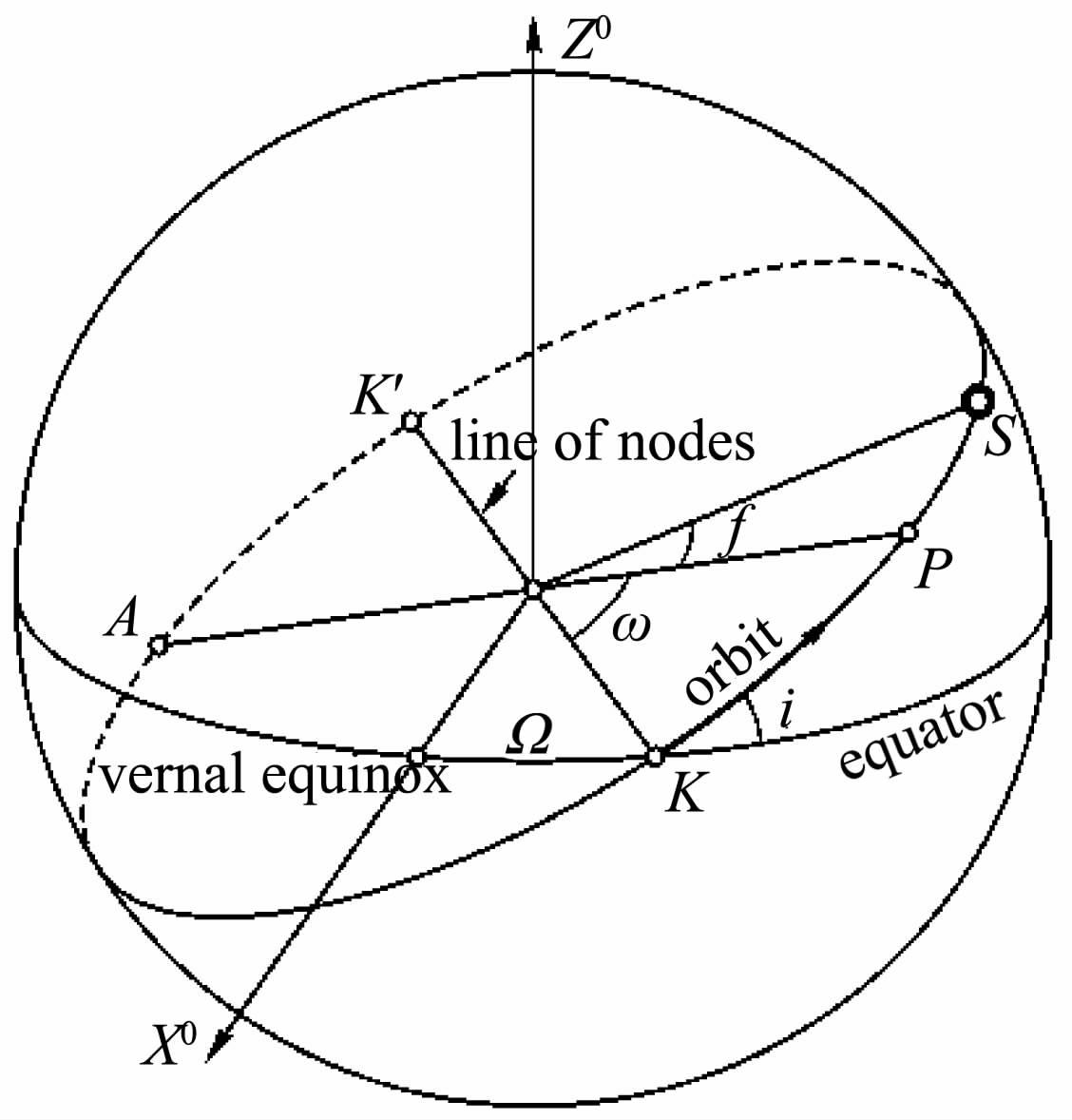
式中,i,Ω,a,e,f是6 个轨道根数,如图 1 所示,其中,i是轨道倾角;Ω 是升交点赤经;a是椭圆轨道面的半主轴;e是椭圆轨道面的偏心率;f是真近点角; n是平均角速度,且满足公式(2):
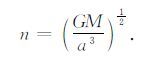
|
(2) |
在实际观测中,卫星除受到万有引力作用外,还受到其它保守力或非保守力的影响,它们通常被称为摄动力或扰动力.在典型的中低轨卫星中,主要包括以下摄动力的模式:行星体非球形引力摄动、第三体引力摄动、太阳和行星表面辐射压、潮汐作用、大气阻力和相对论效应等.此时卫星运动被称为卫星受摄运动.保守力和非保守力作用下轨道微分方程的解分别就是著名的拉格朗日行星运动方程和牛顿行星运动方程.
|
图 1 卫星运行轨道和轨道根数的关系 Fig. 1 Relation of satellite orbits and orbital elements |
当摄动力为保守力时,摄动力可以用位函数R来表示.此时,卫星运动的微分方程为
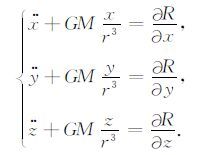
|
(3) |
在摄动力作用下,轨道根数会随时间而发生变化,但是每一个时刻轨道的位置和速度仍可用该时刻的瞬时轨道根数所确定的椭圆来表示,这样的椭圆称为密切椭圆.而卫星的实际运动轨迹就是各个时刻密切椭圆的包络线.
对公式(1)求导就可以建立瞬时情况下卫星轨道根数与卫星位置、速度之间的关系:
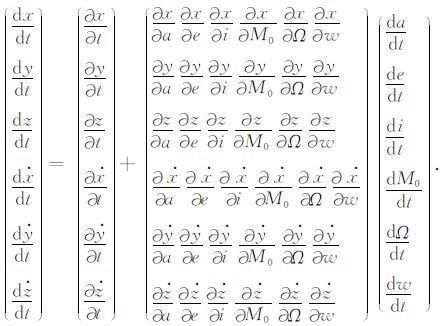
|
(4) |
将公式(1)和公式(3)代入公式(4),整理后得到拉格朗日受摄运动方程:
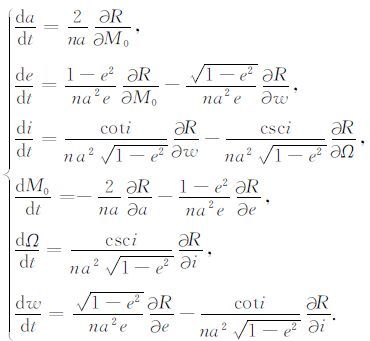
|
(5) |
当摄动力为非保守力时,摄动运动微分方程的解就是牛顿受摄运动方程---公式(6):
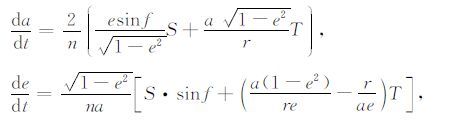
|
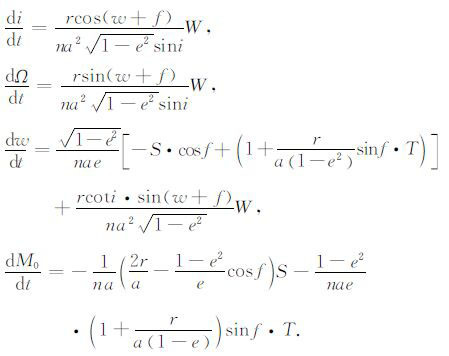
|
(6) |
拉格朗日摄动运动和牛顿摄动运动方程建立了轨道根数与各种摄动力之间的关系,同时公式(1)又建立了轨道根数与卫星的位置、速度之间的关系.于是,各种摄动力与卫星的位置、速度之间就建立了关系.
为了能够解算月球行星重力场模型,还需要建立月球位场与卫星的位置和速度之间的关系.此时就需要引入月球重力位场,而月球重力位场可以展开成球谐场的形式,见公式(7):
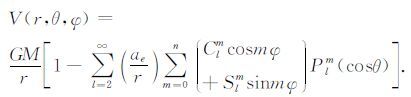
|
(7) |
用公式(7)代替拉格朗日摄动运动方程中的位函数R就可以建立月球重力位场与卫星的位置、速度之间的关系,而此时可把其它的扰动力作为误差并借助拉格朗日摄动运动和牛顿摄动运动方程来剔除.至此,便建立了卫星数据(位置和速度)与月球重力位场之间的关系.利用这一关系就可以计算月球重力球谐场系数,从而建立月球重力场模型.以上原理也是后文提到的GEODYN-II软件计算月球重力场的基础.以上关系的详细推导过程可参考相关物理大地测量学书籍[13-14].
3 GEODYN-II软件移植GEODYN-II/SOLVE 软件是利用轨道动力学的方法来计算月球重力场的[15-16].该软件目前已经开发到第二代,是由NASA 提供支持开发的. NASA 在开发该软件时是面向多个平台的,但是作者只获得了两个工作站版本:v0302版和v0908版. 由于在利用GEODYN-II/SOLVE 解算行星重力场时可以将整体数据分化为多个数据段来进行计算,因此可以将一个总体任务分化为若干个分任务来分别进行处理.基于这个特点多台微机同时计算各个分任务就会在很大程度上超越单台工作站的效率,并且成本更低廉.故可以利用多台微机同时计算以提高计算工作效率、降低成本、扩大使用范围.经测试发现多台微机联合计算可以提高计算效率约5~ 10倍.本文将这两个工作站版本都移植成了微机版本,并在两套操作系统(Fedora Core13 和Solaris 10),3 个编译器(GCC 编译器、Intel 编译器和Solaris Studio 12编译器),2种硬件设备(工作站平台和微机平台)下进行多次测试以确定这两个微机版本的性能优劣.
测试结果表明v0908版的计算结果比v0302版具有明显优势.在短弧段内,v0908版比v0302版的误差小;在长弧段内,v0908 版的误差基本保持不变,而v0302版的误差还有所增大.基于此,本文将利用v0908版为基础,并运用多台微机进行解算,取得了较好的结果.
4 53阶次月球重力位场的求解本文解算月球重力场是利用SELENE 主卫星的轨道数据.卫星轨道高度为100km,时间覆盖范围是2007-10-20-00∶00∶00-2008-10-29-13∶38∶00.数据采样间隔为60s.卫星在月球正面和背面的残差的量级分别为0.6mm/s和30mm/s[12].此次计算将弧段长度选择为14天(覆盖全月球一次).采用的坐标系统是J2000坐标系统,中心选在月球质量中心,时间系统为UT 世界时,月球参考半径为1738.0km,并建立距月球质心为1750km 半径(即距离月球参考半径为12km 高度)的自由空气重力异常场.根据月球空间环境还加了以下改正:行星体中心引力摄动、太阳和地球引力摄动、海潮固体潮引力、极移改正、太阳辐射压、相对论效应等.由于月球没有大气因此不需要考虑大气阻力校正.
利用v0908 微机版本分别解算出40 阶次、50 次阶、53阶次、55阶次、58阶次、60阶次月球自由空气重力异常场,见图 2-5.
|
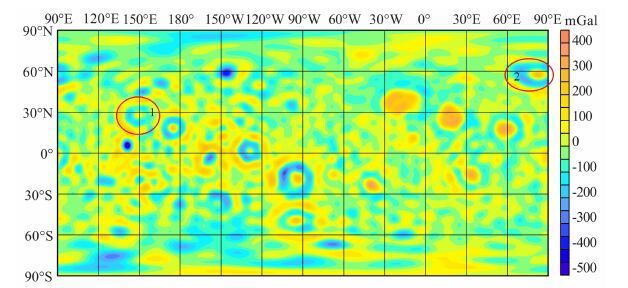
图 2 40阶次月球自由空气重力异常场(区域1为莫斯科海,区域2为洪保德海) Fig. 2 A map of free air gravity anomalies field of the moon at degree 40 (Mare Mosco-viense in the 1st zone,and Mare Humboldtianum in the 2nd zone) |
|
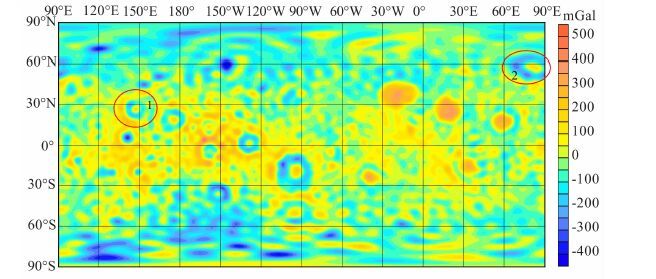
图 3 50阶次月球自由空气重力异常场(区域1为莫斯科海,区域2为洪保德海) Fig. 3 A map of free air gravity anomaly field of the moon at degree 50 (Mare Mosco-viense in the 1st zone,and Mare Humboldtianum in the 2nd zone) |
|
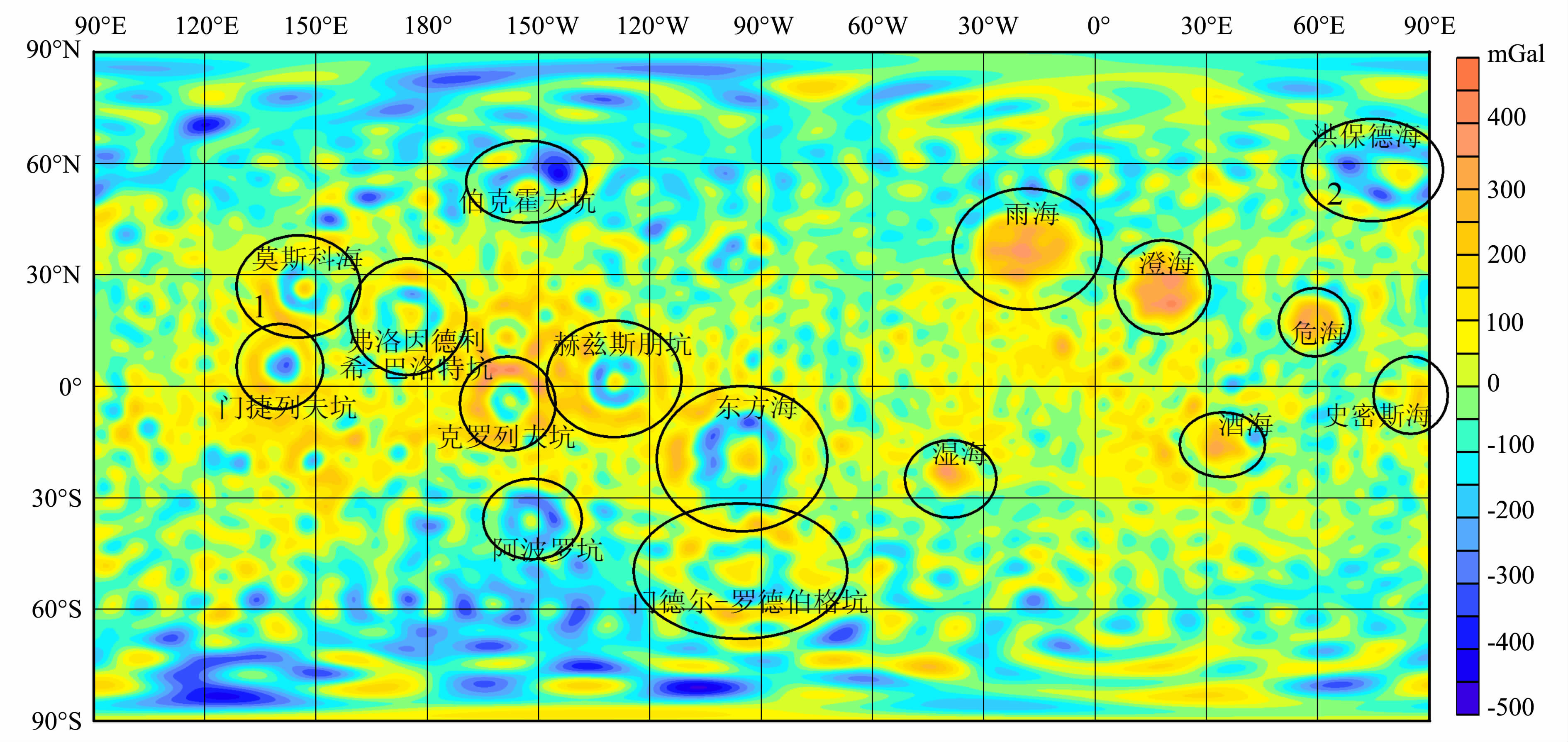
图 4 53阶次月球自由空气重力异常场(区域1为莫斯科海,区域2为洪保德海) Fig. 4 A map of free air gravity anomaly field of the moon at degree 53 (Mare Moscoviense in the 1st zone,and Mare Humboldtianum in the 2nd zone) |
|
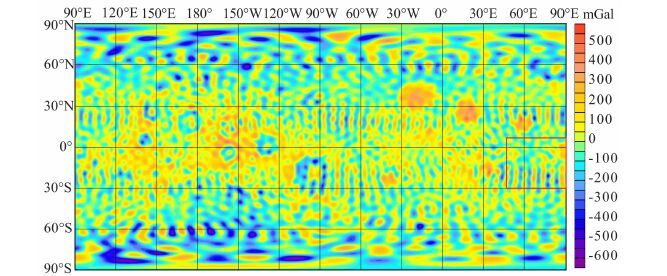
图 5 60阶次月球自由空气重力异常场 Fig. 5 A map of free air gravity anomaly field of the moon at degree 60 |
对比图 2、3、4的区域1莫斯科海(27.3°N,147.9°E) 可以看出50阶次能够比40阶次更精细地反映重力异常的变化,53阶次又比50阶次所有提高.对比这三个图的区域2还显示出在50 阶次自由空气重力异常图中的洪保德海(56.8°N,81.5°E)(图 3 区域2)的中心高异常周围的环状异常是由多个小的负异常组成的,并不是像40阶次(图 2区域2)所反映的是由一个负异常环形成的,而53阶次(图 4区域2) 较50阶次更能精细地反映多个负异常轮廓.由此看出,随着解算阶次的升高,其精度也随之提高,其所反映的构造也更加精细.然而,当计算的阶次提高到53阶次以上时,则会产生一种平行于经线的异常特征(如图 5中60阶次所示的红色区域,凡高于53阶次都有如此特征,因此未绘制55 阶次和58 阶次自由空气重力异常图,且阶次越高噪声越大).理论表明[17]100km 高度、采样间隔是60s的轨道数据是可以计算出60阶次的重力场模型,但是实际计算过程中发现在接近理论阶次(60阶次)时,最后几个阶次的模型会产生上面那样平行于经线的异常特征(图 5的红色区域),而实际上这种异常是一种高频噪声.因此本文选择53 阶次月球球谐位场模型(图 4)---LG-53作为最后解算的结果.
5 53 阶次月球重力场与其它重力场的对比 5.1 与日本SGM-90d(90阶次)模型对比与日本公布的90阶次SGM-90d[12]自由空气重力异常图(图 6)进行对比,二者重力异常表现一致,如月球正面最大的五个月海地区(图 4、图 6中的雨海、澄海、危海、酒海、湿海)以及东方海等所体现的重力异常特征是相同的,由此证明解算结果的可靠性.但对于解算阶次来说仍有所差距,90 阶次重力场(SGM90d)大约能反映60km 左右的重力异常变化,而53阶次(LG-53)大约反映100km 左右的异常变化[17],从图 4和图 6也可以看出一些小的构造特征在53阶次自由空气重力异常场中表现还不明显,如图 4 中位于月球背面的克罗列夫坑(4.0°S,157.4°W),但是总体趋势表现一致.

|
图 6 SELENE 官方公布的利用SGM90d模型计算得到的自由空气重力异常图 Fig. 6 A map of free air gravity anomalies for SGM90d released by SELENE official |
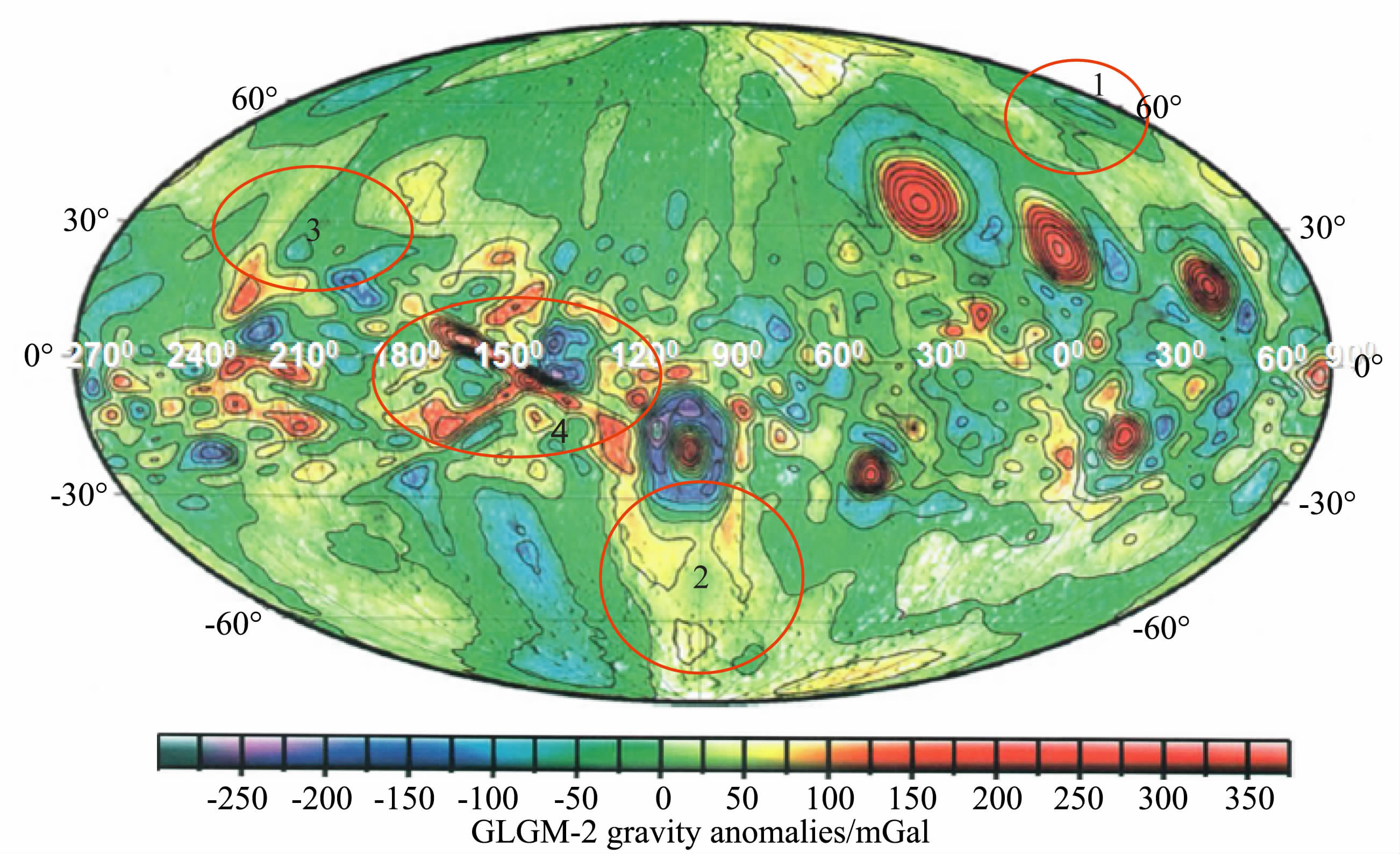
与GLGM-2所建立的自由空气重力异常图(图 7)对比发现:图 7中区域1 的位置在图 4 中应该对应的是洪保德海(56.8°N,81.5°E).在图 4中可以看到洪保德海的重力异常特征,而在GLGM-2(图 7)中却没有显示出来;同样,图 7中的区域2和区域3的位置在图 4中分别对应的是门德尔-罗德伯格坑(50.0°S,94.0°W)和莫斯科海(27.3°N,147.9°E),在图 7 中也都没显示出来.图 7 中的区域4 对应于图 4 的克罗列夫坑(4.0°S,157.4°W)和赫兹斯朋坑(2.6° N,129.2°W).在图 4 中可以很清晰地看到它们的重力异常特征,而在GLGM-2 中的这两个坑的重力异常已经混成了一种类似线状的重力异常特征,很容易产生错误的解释.以上说明GLGM-2 在大于南北纬30°的地区已经不能反映出有效的重力异常了,同时在月球背面的结果也不能作为解释的依据,甚至有些地方是错误的,而LG-53 建立的自由空气重力异常的结果却能反映出明显而清晰的重力异常特征.
|
图 7 GLGM-2(70th阶次)建立的自由空气重力异常图[8] Fig. 7 A map of free air gravity anomalies for GLGM-2 model (70th degree) |
正是由于建立GLGM-2 模型所参与计算的轨道数据都是局限在赤道附近(轨道倾角较小)、轨道高度很高,且缺少月球背面数据.这就说明了对于非极轨的轨道覆盖率不能达到全球覆盖;高轨道数据不能精确地反映月球重力异常特征的精细变化;缺少月球背面的直接探测数据是无法在该地区建立准确的重力异常场的.
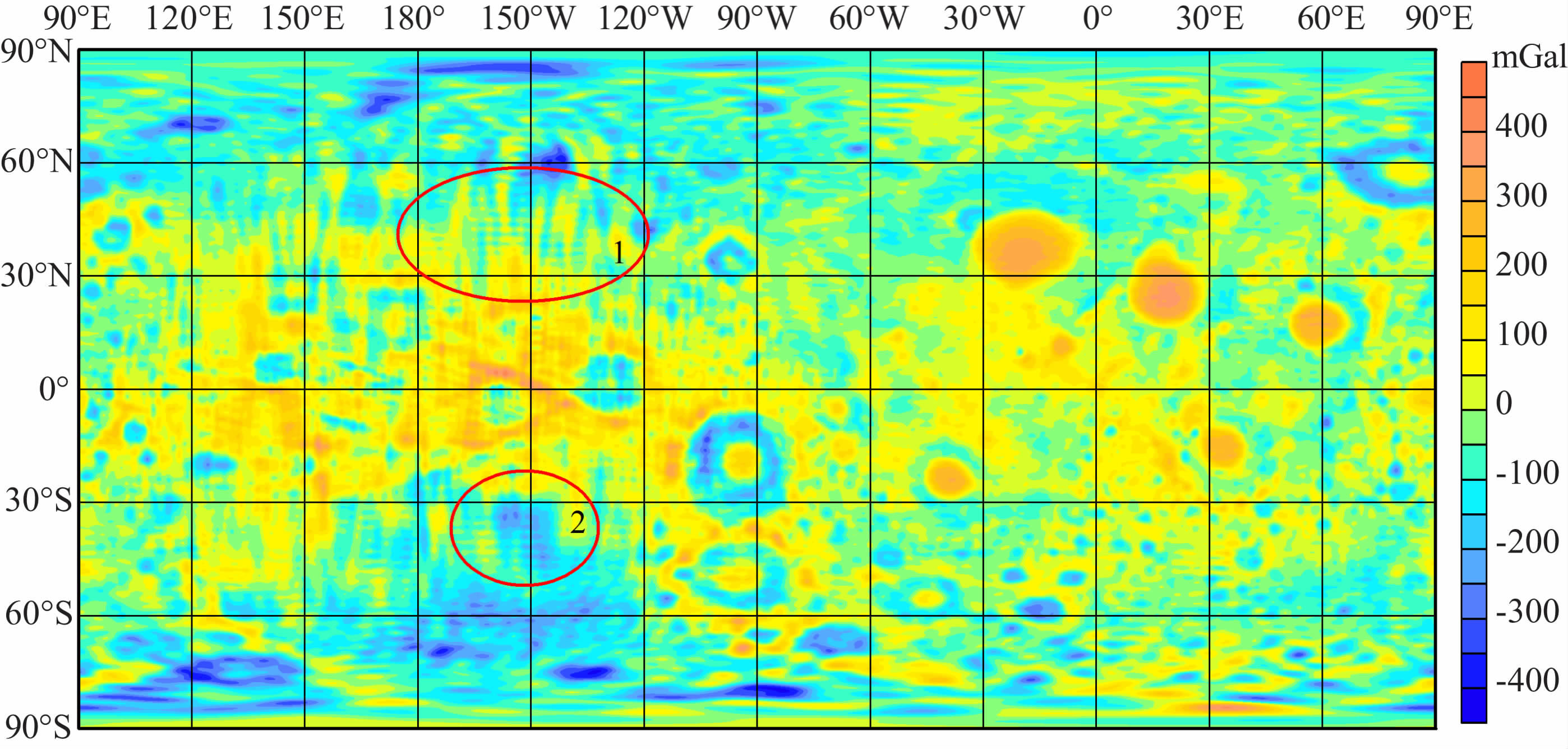
5.3 与美国LP165P(165阶次)模型对比由于缺少月球背面卫星轨道的直接探测数据,所以在解算LP165P时要增加一个Kaula约束以便使求解出的结果不会产生很大的震荡.图 8 便是借助Kaula约束建立的LP165P月球自由空气重力异常图.
|
图 8 LP165P模型自由空气重力异常图 Fig. 8 A map of free air gravity anomalies for LP165P gravity model |
对比LG-53和LP165P所建立的月球自由空气重力异常图可以看出:
(1) 如图 8区域1所示,LP165P 模型在月球背面区域中有明显的毛刺状的噪声干扰.正如Konopliv等[10]所指出的一样,由于缺少月球背面数据导致了这种高频噪声的产生,且使得LP165P 在月球背面的有效阶次只能达到60阶次.
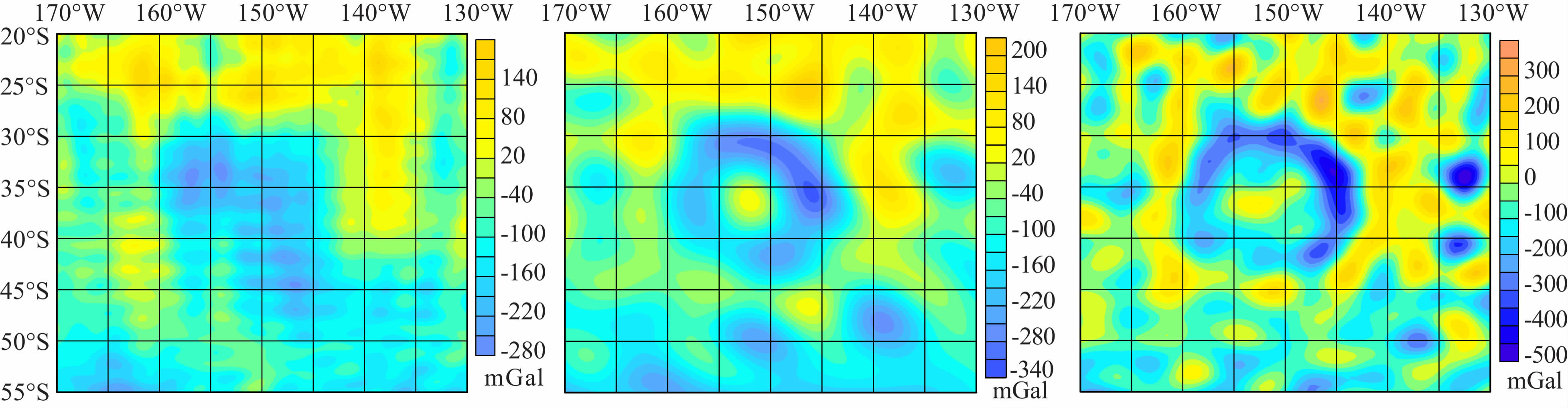
(2) 从精度对比来看,在月球背面区域,LG-53 所建立的自由空气重力异常图(图 4)要比LP165P 模型所建立的自由空气重力异常(图 8)的精度要高.本文特别选择Apollo坑的重力异常特征来说明这一问题.图 8 中的区域2 就是Apollo坑,其详图可见图 9.图 9 是LP165P、LG-53 和SGM90d 在Apollo坑所反映的自由空气重力异常特征的对比. 图 9表明LP165P 在Apollo坑所反映的重力异常特征具有明显的噪声干扰,甚至淹没了原本真实的重力异常特征,给地球物理解释带来困难,而LG-53 比LP165P 的效果有明显优势,能够反映出精度较高的重力异常特征,SGM90d的精度在三者中是最高的.由此,LG-53所反映的月球背面自由空气重力异常特征的精度比LP165P要高,且无噪声干扰,能够用于地球物理解释.
|
图 9 Apollo坑自由空气重力异常(左:LP165P;中:LG-53;右:SGM90d) Fig. 9 Free air gravity anomalies in Apollo crater for (Left: LP165P; Middle: LG-53; Right: SGM90d) |
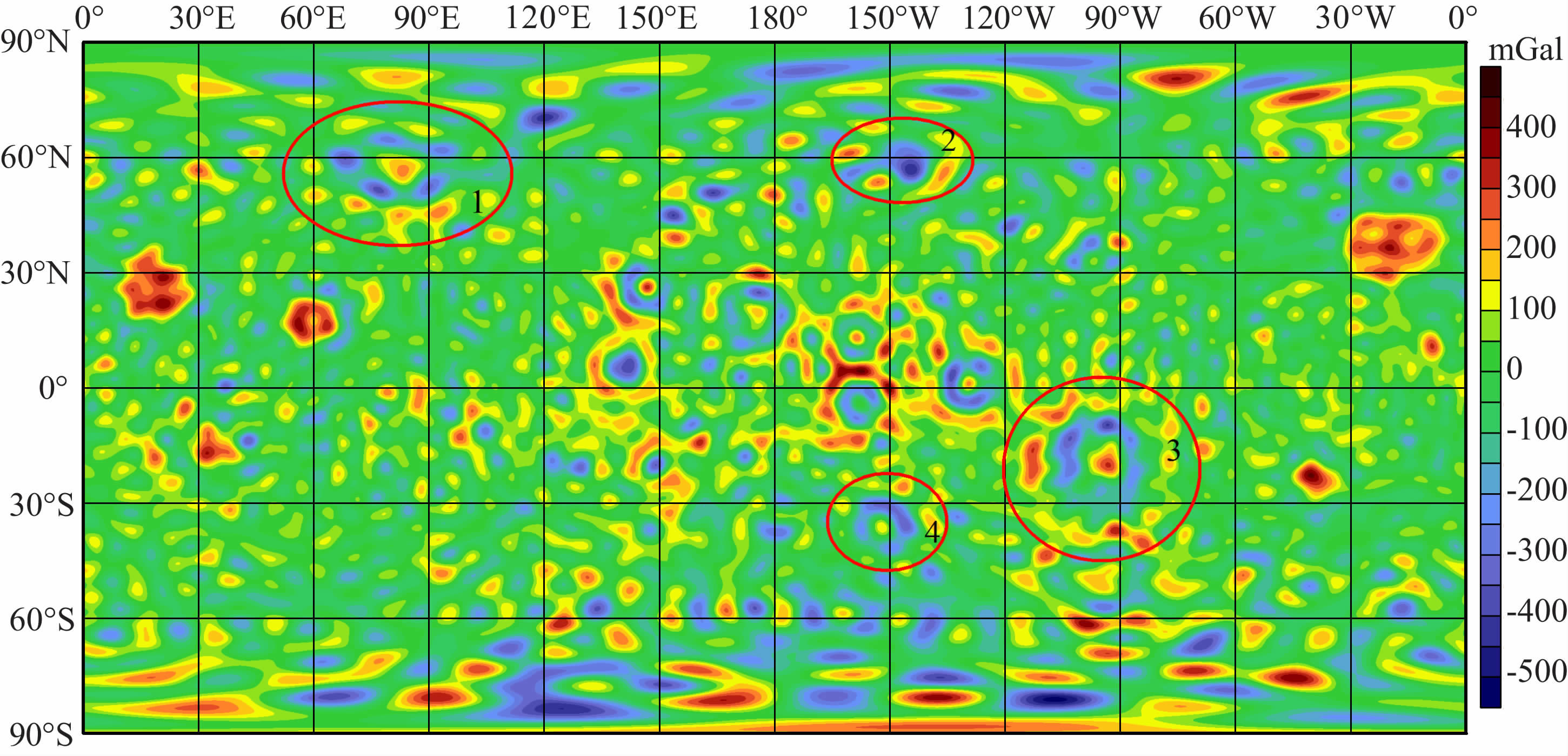
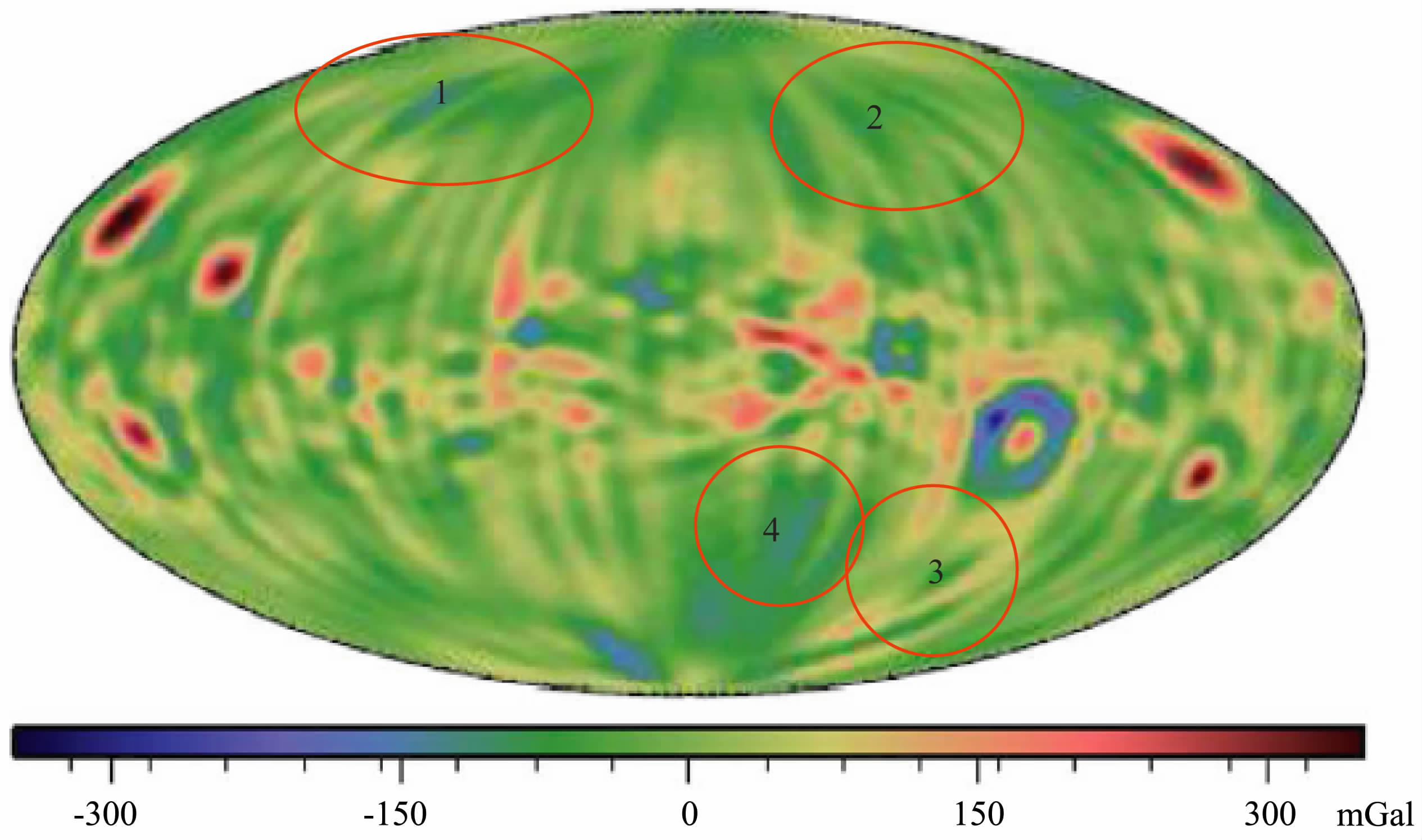
本文利用LG-53 并借助月球地形模型STM359_grid02_180(180阶次)计算得到月表重力异常场图并与Yan 等[18]建立的CEGM-01 月表重力异常场图进行对比,如图 10、11 所示.首先,CEGM-01月表重力异常图(图 11)存在许多在全球范围内与经线平行的线性重力异常特征.实际上,这种线性的重力异常特征是不存在的.出现这一现象的原因类似于上面提到的接近理论阶次时重力异常图所反映出的高频噪声.也就是说CEGM-01 所计算出的50阶次月球重力场的实际有效阶次达到不了50阶次,后几个阶次的结果误差较大.与此同时,还可以看出,LG-53 无论是在月球高纬度地区还是在月球背面反映的重力场信息都能够较CEGM-01 结果更精确.首先最明显的是在大于北纬30°地区的洪保德海(56.8°N,81.5°E)(图 10、11 的区域1) 的重力异常在LG-53 中有反映,而在CEGM-01 中却非常不明显.同样的,在背面也是如此,如伯克霍夫坑(54.7°N,114.6°W)(图 10、11 的区域2)的重力异常和正对东方海下面的门德尔-罗德伯格坑(50.0°S,94.0°W)(图 10、11的区域3)的重力异常,以及阿波罗坑(36.1°S,151.8°W)(图 10、11的区域4)的重力异常也都有类似的特征.诸如此类,因此LG-53所建立的月表重力异常在大于南北纬30°地区和在月球背面地区都有明显优势.
|
图 10 LG-53(53阶次)重力场计算得到的月表重力异常图 Fig. 10 A map of gravity anomalies on lunar surface for LG-53 (53rd degree and order) gravity model |
|
图 11 CEGM-01(50th阶次)月表重力异常图[18] Fig. 11 A map of gravity anomalies on lunar surface for CEGM-01 (50th) |
在月球重力场中一个最显著的特点就是那些具有高重力异常特征和低矮月球地形特征的盆地.
Muller和Sjogren 称其为Mascon 盆地[19].在此需要注意的是,虽然Mascon 当初在命名时表示的是massconcentration,但是其地质含义并不与它的中文译名一样是与“质量瘤"有关.因为到目前为止,只能证明它只是与高重力异常有关,但是是否与地下高密度体物质有关并没有得到证实,且有资料表明这种高重力异常与壳幔界面的起伏可能有关[20].因此,下文即使使用Mascon,也只是作为名称引用.
结合月球地形图(如图 12)和本文计算得到的自由空气重力异常图(图 4)可以归纳出以下四个类型Mascon的重力异常和月球地形特征.

|
图 12 月球地形图(STM359_grid02_180-180阶次)[21] Fig. 12 Topography of the moon for STM359_grid02_180 (180th) |
第一,雨海(图 13)、澄海(图 14)、危海(图 15)、 湿海、史密斯海这几个Mascon存在以下几个特点:
(1) 在这些Mascon 的中心区域有较高的重力异常值,且在该区域内部还存在多个更高的异常点;
(2) 对于地形来说,对应于这些高重力异常区域的是低矮的地形,且是一个面积较大的平坦区域;
(3) 具有以上特点的Mascon 都位于月球的正面地区;
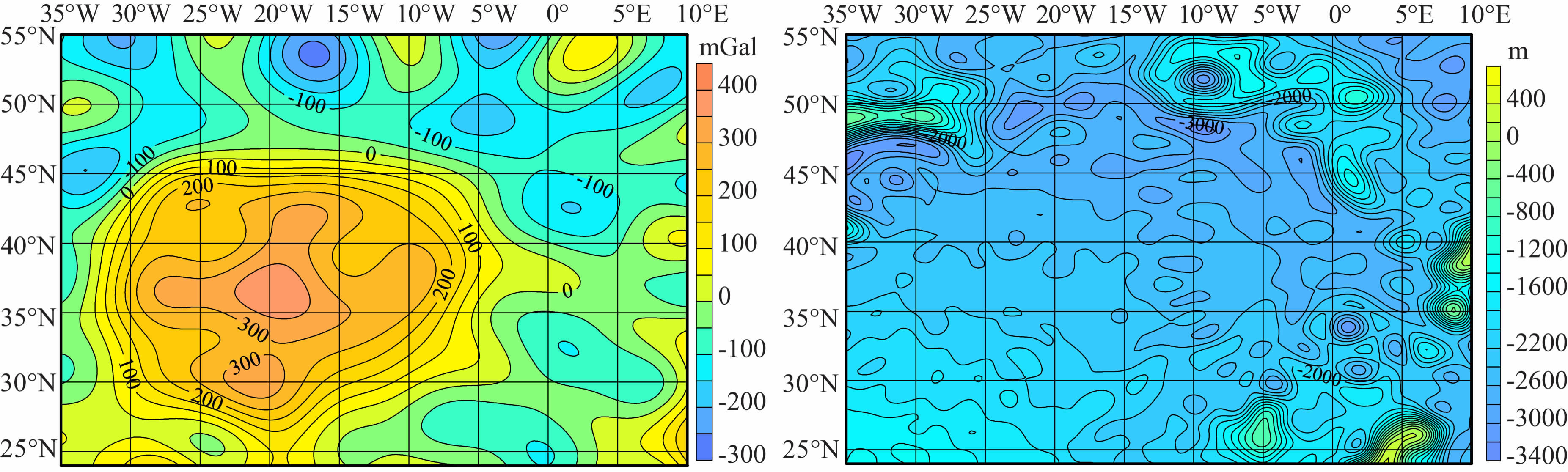
|
图 13 雨海自由空气重力异常图(来自LG-53)(左)和月形图(来自STM359_grid)(右) Fig. 13 Free air gravity anomaly field (for LG-53) (left) and topography (for STM359_grid02_180) (right) in Mare Imbrium |
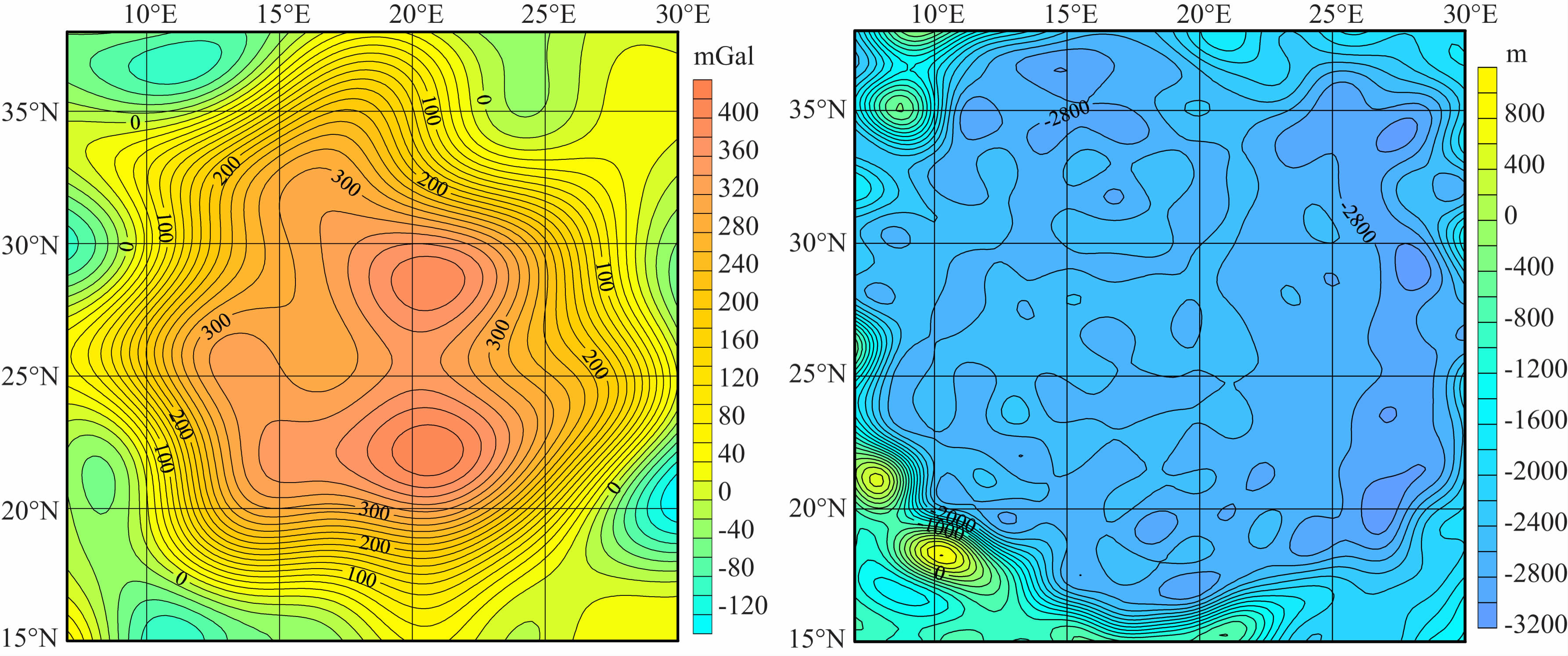
|
图 14 澄海自由空气重力异常图(来自LG-53)(左)和月形图(来自STM359_grid)(右) Fig. 14 Free air gravity anomaly field (for LG-53) (left) and topography (for STM359_grid02_180) (right) in Mare Serenitatis |
|
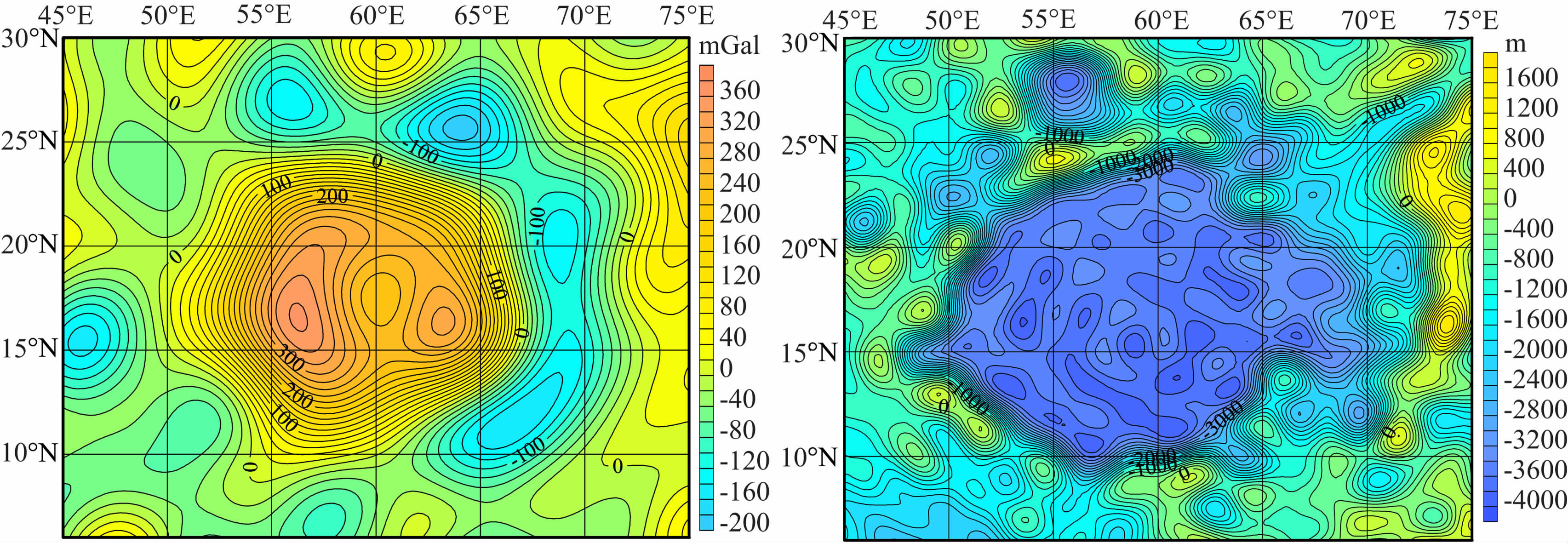
图 15 危海自由空气重力异常图(来自LG-53)(左)和月形图(来自STM359_grid)(右) Fig. 15 Free air gravity anomaly field (for LG-53) (left) and topography (for STM359_grid02_180) (right) in Mare Crisium |
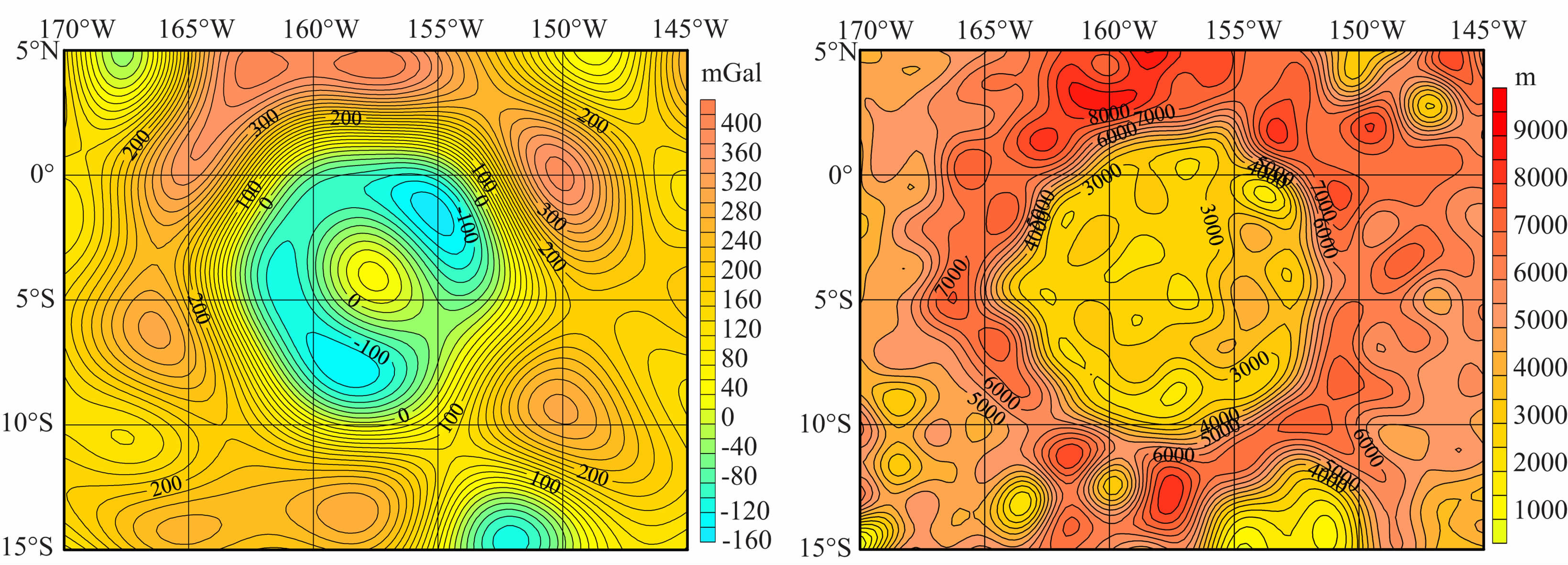
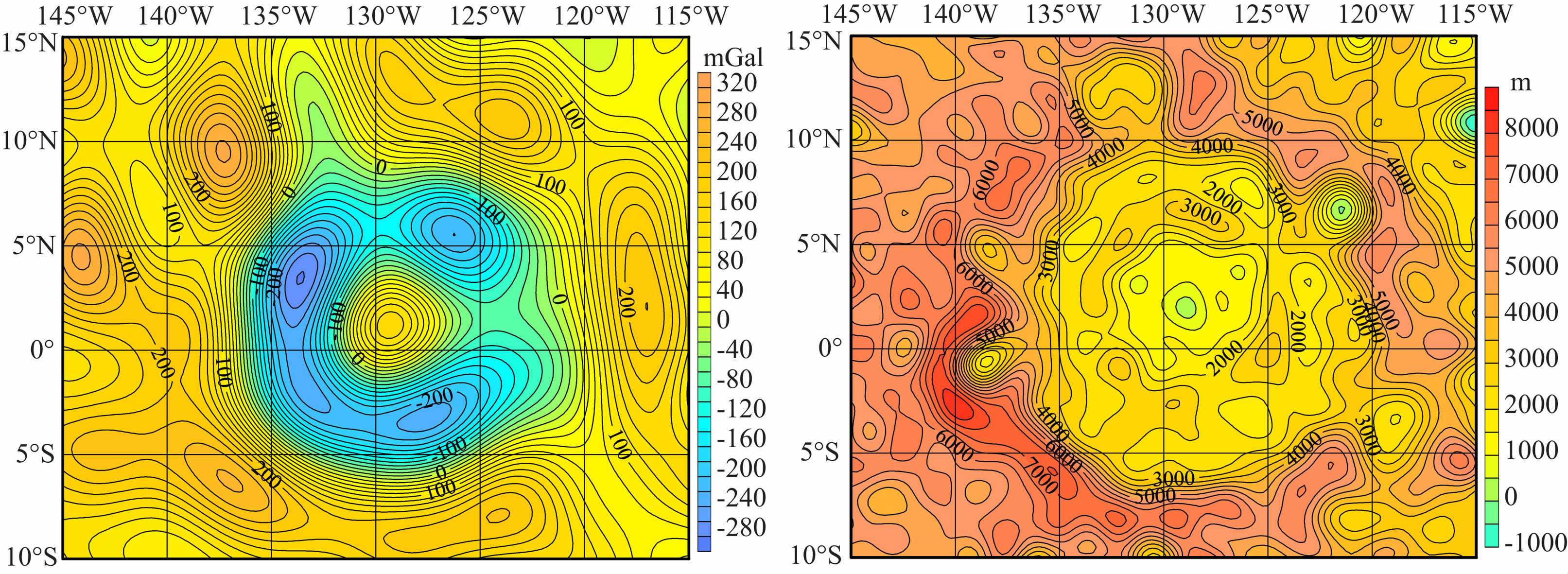
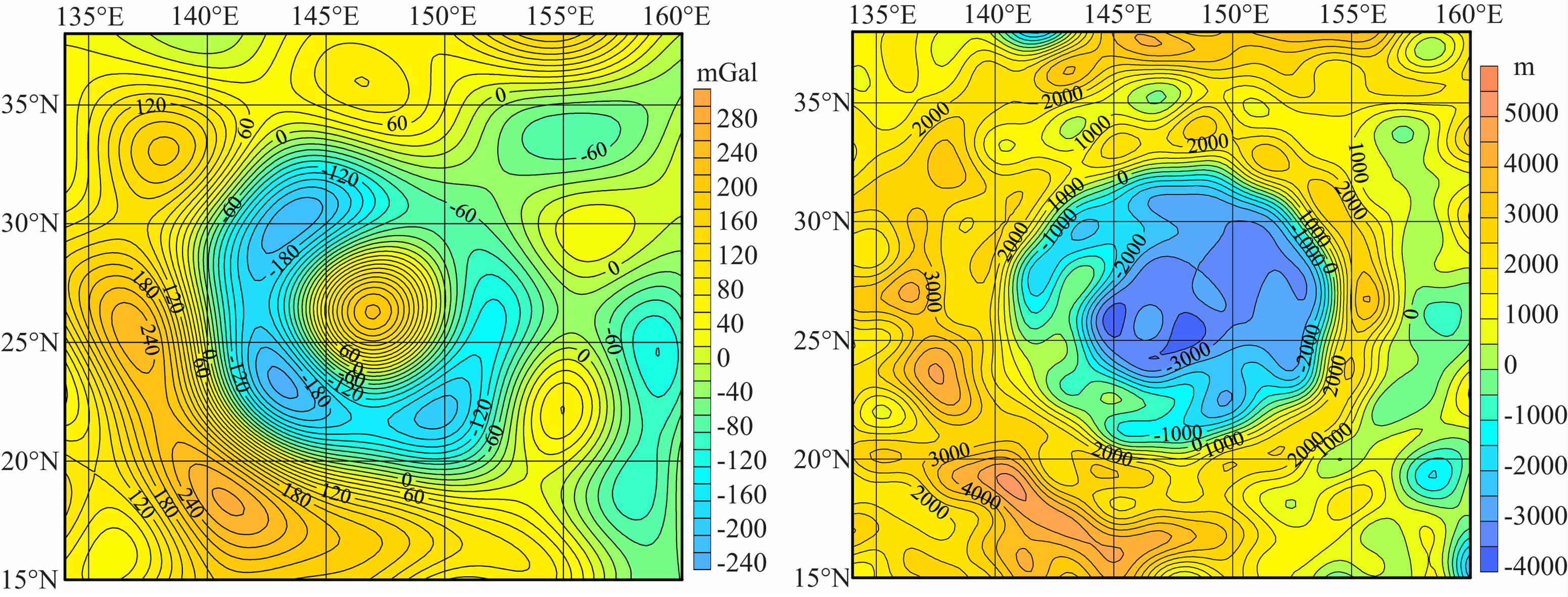
第二,克罗列夫坑(图16)、赫兹斯朋坑(图17)、 莫斯科海(图18)等,其重力异常特征表现为:
(1) 这些坑表现为双环型重力异常特征,即由最外面的高重力异常环和中间的较低的重力异常环所围绕,而在双环的中心则只出现一个高重力异常点;
(2) 在低重力异常环中具有明显的多个更低的重力异常点;
(3) 对应月形来说,这种月坑的中间地区地形较低,且在地形变化的圆形边界处呈陡然变化的趋势;
(4) 具有以上这些特征的Mascon主要分布在月球背面地区;
|
图 16 克罗列夫坑自由空气重力异常图(来自LG-53)(左)和月形图(来自STM359_grid)(右) Fig. 16 Free airgravity anomaly field (forLG-53) (left) and topography ((or STM359_grid02_180) (right) in Crater Korolev |
|
图 17 赫兹斯朋坑自由空气重力异常图(来自LG-53)(左)和月形图(来自STM359_grid)(右) Fig. 17 Free air gravity anomaly field (for LG-53) (left) and topography (for STM359_grid02_180) (right) in Crater Hertzsprung |
|
图 18 莫斯科海自由空气重力异常图(来自LG-53)(左)和月形图(来自STM359_grid)(右) Fig. 18 Free air gravity anomaly field (forLG-53) (left) and topography (for STM359_grid02_180) (right) in Mare Moscoviense |
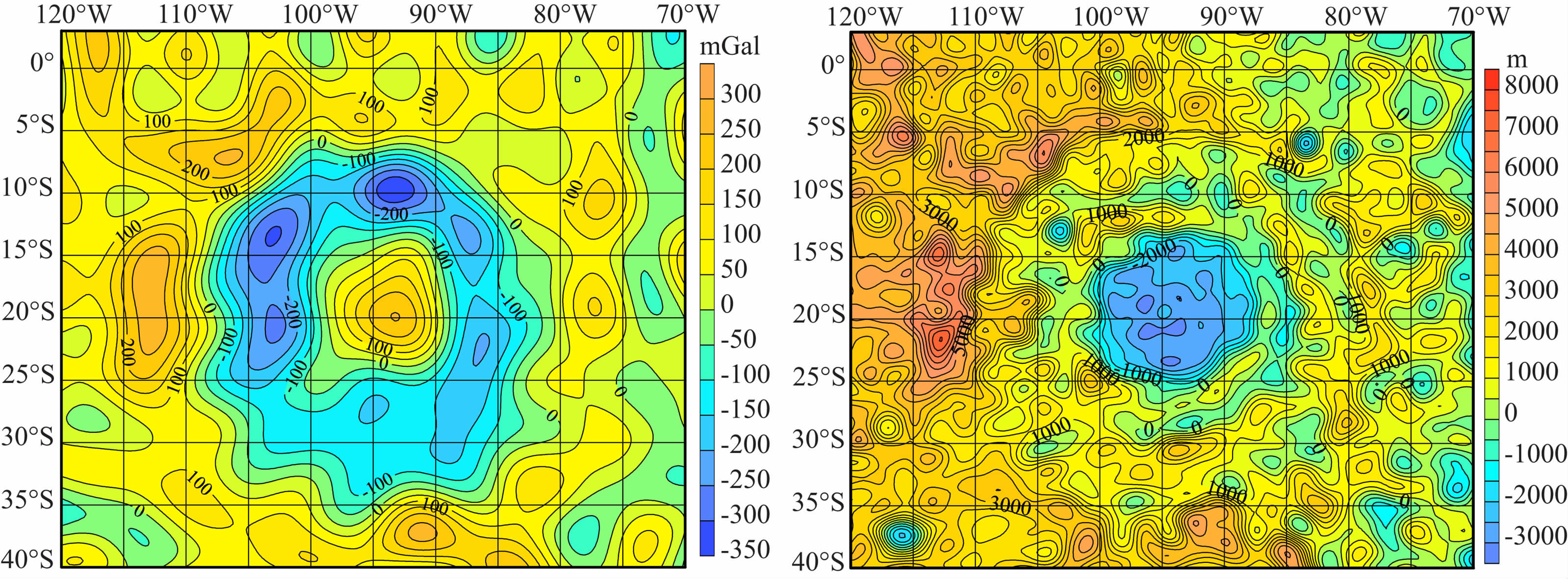
第三,特殊的东方海(如图19):
与上面第二种不同的是,虽然东方海也具有双环型重力异常特征,即最外圈是高重力异常环,内部是低重力异常环,最中心是一个高重力异常点,但是最大不同来自地形的差异.东方海的地形特征是多环型的.最外环是高地形,然后是低地形、再是高地形,中间又是低地形,且中心低地形的范围较大.
|
图 19 东方海自由空气重力异常图(来自LG-53)(左)和月形图(来自STM359_grid)(右) Fig. 19 Free air gravity anomaly field (for LG-53) (left) and topography (for STM359_grid02_180) (right) in Mare Orientale |
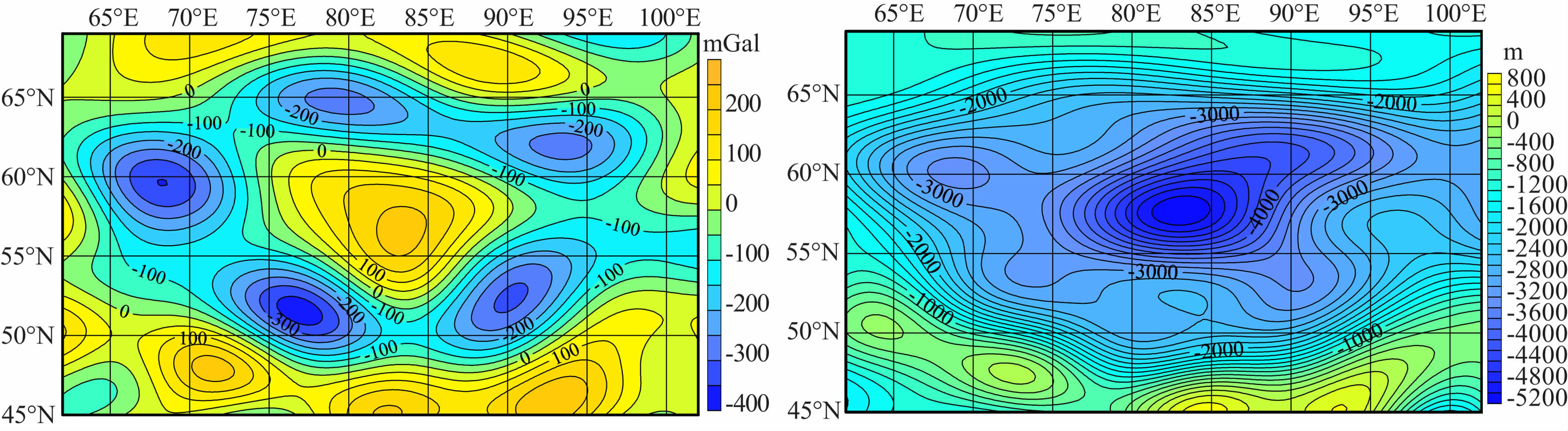
第四,另外一个较特殊的是洪保德海(图 20): 与其它Mascon差异较大,其中心有一个高异常而被周围多个低异常点所环绕,且低异常的范围较大. 对于该地地形特征来说,它是一个低矮地形且面积较大,地形向中间逐渐降低,而在中心地带出现一个梯度变化较大的低洼地.
|
图 20 洪保德海自由空气重力异常图(来自LG-53)(左)和月形图(来自STM359_grid)(右) Fig. 20 Free air gravity anomaly field (for LG-53) (left) and topography (for STM359_grid02_180)(right) in Mare Humboldtianum |
综上所述,这些Mascon 所表现的重力异常特征和地形特征可以归为四类:第一类是具有高重力异常和中心平坦的低地形的Mascon,像雨海、澄海、 危海、湿海、史密斯海;第二类是具有双环型重力异常特征且在地形变化的边界处突然降低的Mascon,如克罗列夫坑、赫兹斯朋坑和莫斯科海等;第三类和第四类是两个比较特殊的Mascon,东方海和洪保德海,东方海的重力异常也是双环型的,但是其地形具有多环型的特征;而洪保德海周围的多个低异常点的范围较大,且地形向中间逐渐降低面积也较大,中心地带出现一个梯度变化较大的低洼地.
7 结论第一,本文通过回顾和分析月球重力场探测历史了解到获得高精度月球重力场的影响因素是:轨道高度、轨道采样率、轨道倾角和借助中继卫星获得月球背面的直接探测数据.
第二,本文利用自行移植的GEODYN-II软件和SELENE 官方公布的100km、60s数据间隔的轨道数据建立了53阶次月球重力位场LG-53.其移植版本的计算效率要比原始工作站的计算效率要高5~10 倍.在实际计算过程中发现当解算出的阶次接近理论阶次(60阶次)时,会出现平行于经线的高频噪声,因此最终选择53阶次作为本文的最后结果.
第三,利用计算得到的月球重力位场LG-53模型建立了自由空气重力异常和月表重力异常.将其与GLGM-2(70 阶次)、LP165Q(165 阶次)以及CEGM-1(50阶次)对比发现本文计算得到的重力图的准确性和可靠性较高可以利于后续地质和地球物理解释.与日本在SCIENCE 上公布的SGM90d 的重力异常图对比具有一致性,但阶次上还有差异. 寄希望于官方提供更高精度的探测数据.
第四,本文还结合53阶次重力异常与月球地形模型(STM359_grid02_180)探讨了四种类型Mascon的重力异常特征和月球地形特征.
致谢首先感谢JAXA 提供的SELENE 轨道数据.感谢常晓涛处长和孙玉所提供的GEODYN-II 软件的工作站版本技术支持.
| [1] | Akim E L. Determination of the gravitational field of the Moon from the motion of the artificial lunar satellite "Lunar-10 ". Dokkl. Akad. Nauk SSSSR , 1966, 170: 799-802. |
| [2] | Michael W H, Blackshear W T. Recent results on the mass, gravitational field and moments of inertia of the Moon. Earth Moon and Planets , 1972, 3(4): 388-402. |
| [3] | Lorell L, Sjogren W L. Lunar gravity: Preliminary estimates from lunar orbiter. Science , 1968, 159(3815): 625-627. DOI:10.1126/science.159.3815.625 |
| [4] | Anderson K A, Chase L M, Lin R P, et al. Subsatellite measurements of plasma and energetic particles // Apollo 16 Prelim. Sci. Rept., NASA SP-315. Washington D C, 1972, 22: 1-6. |
| [5] | Bills B G, Ferrari A J. A harmonic analysis of lunar gravity. J. Geophys. Res. , 1980, 85(B2): 1013-1025. DOI:10.1029/JB085iB02p01013 |
| [6] | Bills B G, Ferrari A J. A lunar density model consistent with topographic, gravitational, librational, and seismic data. J. Geophys. Res. , 1977, 82(8): 1306-1314. DOI:10.1029/JB082i008p01306 |
| [7] | Konopliv A S, Sjogren W L, Wimberly R N, et al. A high resolution lunar gravity field and predicted orbit behavior // AAS/AIAA Astrodynamics Specialist Conference, Victoria, B C: Canada, 1993: 93-622. |
| [8] | Lemoine F G R, Smith D E, Zuber M T, et al. A 70th degre lunar gravity model (GLGM-2) from Clementine and other tracking data. J. Geophys. Res. , 1997, 102(E7): 16339-16359. DOI:10.1029/97JE01418 |
| [9] | Konopliv A S, Yuan D N. Lunar prospector 100th degree gravity model development. // 30th Annual Lunar and Planetary Science Conference. No. 1067, Houston, 1999. |
| [10] | Konopliv A S, Asmar S W, Carranza E, et al. Recent gravity models as a result of the Lunar Prospector mission. Icarus , 2001, 150(1): 1-18. DOI:10.1006/icar.2000.6573 |
| [11] | Wieczorek M A, Jolliff B L, Khan A, et al. The constitution and structure of the lunar interior. Reviews in Mineralogy and Geochemistry , 2006, 60(1): 221-364. DOI:10.2138/rmg.2006.60.3 |
| [12] | Namiki N, Iwata T, Matsumoto K, et al. Farside Gravity field of the Moon from four-way doppler measurements of SELENE (Kaguya). Science , 2009, 323(5916): 900-905. DOI:10.1126/science.1168029 |
| [13] | Kaula W M. Theory of Satellite Geodesy. Waltham, M A: Blaisdell Publishing Company, 1966 . |
| [14] | Hofmann-ellenhof B, Moritz H. Physical Geodesy. Wien & New York: Springer, 2005 . |
| [15] | Eddy W F, McCarthy J J, Pavlis D E, et al. GEODYN-II Manual I-V. USA: NASA, 1990 . |
| [16] | Ullman R E. SOLVE Program: Mathematical formulation and guide to user input, Hugher/STX contractor report. Contact NAS5-31760, Greenbelt, Maryland: NASA Goddard Space Flight Center, 1994 . |
| [17] | 陈俊勇, 宁津生, 章传银, 等. 在嫦娥一号探月工程中求定月球重力场. 地球物理学报 , 2005, 48(2): 275–281. Chen J Y, Ning J S, Zhang C Y, et al. On the determination of lunar gravity field in the Chinese first Lunar Prospector mission. Chinese J. Geophys.(in Chinese) (in Chinese) , 2005, 48(2): 275-281. |
| [18] | Yan J G, Ping J S, Li F, et al. Chang'E-1 presion orbit determination and lunar gravity field solution. Adv. Space Res. , 2010, 46(1): 50-57. DOI:10.1016/j.asr.2010.03.002 |
| [19] | Muller P M, Sjogren W L. Mascons: lunar mass concentrions. Science , 1968, 161(3842): 680-684. DOI:10.1126/science.161.3842.680 |
| [20] | Wise D U, Yates M T. Mascons as structural relief on a lunar 'moho’. J. Geophys. Res. , 1970, 75(2): 261-268. DOI:10.1029/JB075i002p00261 |
| [21] | Araki H, Tazawa S, Noda H, et al. Lunar global shape and polar topography derived from Kaguya-LALT laser altimetry. Science , 2009, 323(5916): 897-900. DOI:10.1126/science.1164146 |
 2012, Vol. 55
2012, Vol. 55

