2. 中国科学院研究生院, 北京 100049;
3. GNSS Research Centre, Department of Spatial Sciences, Curtin University, Perth 6845, Australia;
4. Delft Institute of Earth Observation and Space Systems, Delft University of Technology, 2600 GB Delft, The Netherlands
2. Graduate University of Chinese Academy of Sciences, Beijing 100049, China;
3. GNSS Research Centre, Department of Spatial Sciences, Curtin University, Perth 6845, Australia;
4. Delft Institute of Earth Observation and Space Systems, Delft University of Technology, 2600 GB Delft, The Netherlands
基于非差观测值的精密单点定位(PPP)可服务于高精度定位、授时和大气延迟提取等领域[1-6].与相对定位相比,PPP 可利用IGS(International GNSS Service)等机构播发的卫星轨道、钟差产品,在确保高精度的同时,亦避免了生成双差GPS观测值所引起的数据利用率降低、计算量增加等问题[7-8].
然而,PPP 易受两因素的限制[9]:1.实时性: IGS播发的精密卫星轨道、钟差产品是PPP 实施的前提,该类产品的时延一般为2周,难以有效满足大部分实时或近实时PPP 用户的需求;2.收敛时长: GPS 非差相位观测值中所含的卫星相位偏差(Satellite Phase Biases,SPBs)与非差整周模糊度难以分离[10-11],致使PPP各类估值均为模糊度浮点解,其收敛性较差:以静态PPP 为例,位置解收敛至厘米级精度一般需要0.5h 以上;而对于高动态定位应用而言,收敛时间可达1~2h,甚至更长[4-5].
当前,借由各种通讯技术以及数据处理方法的发展,利用局部或全球区域的参考站网,实时估计、 播发和接收GPS 卫星的实时轨道和钟差等产品已取得较大的研究进展:文献[12-14]的结果表明,在考虑数据传输和处理时延后,实时PPP 的定位精度可达厘米-分米级,可满足大部分实时的应用需求.
另一方面,针对PPP 的收敛性问题,若能有效利用GPS相位模糊度的整数特性,则可望缩短收敛时长,且保证定位解的高精度.原因在于:整周模糊度固定后,相位观测值成为类似于伪距的绝对观测量,但测距精度高达毫米级.国内外PPP 模糊度固定的研究工作目前刚刚起步,且主要形成了两种数据处理方案[15],其基本原理为采用全球[10, 16]或广域[17-18]参考站网的GPS 观测数据,直接分离SPBs 的小数部分[10, 15, 17-20](称之为“非整法")或估计包含SPBs的去耦卫星钟差(Decoupled Satellite Clocks,DSCs)[16, 21-22](称之为“去耦法"),用于改正区域内的PPP观测值,以实现非差模糊度固定.
然而,现有PPP 模糊度固定方案存在如下缺陷:(1)非整法或去耦法实施过程中,SPBs的动态模型选取存在矛盾:其中,非整法假定SPBs仅随时间缓慢变化,且其时变部分可通过取平均加以消除[10, 15];与之相反,去耦法则认为SPBs的时变特性难以有效描述,故将其与卫星钟差合并估计,由此形成了一组具有白噪声性质、且与频率有关的新卫星钟差参数[16, 22];(2)经由SPBs或DSCs改正后的非差相位观测值,其模糊度虽具备整数的特性,但依然包含了各种系统误差,尤其是电离层延迟的影响[19-20].由此,整周模糊度的固定仍需基于较长时段的观测数据,以确保其可靠性.研究表明,静态PPP 模糊度固定所需时长约为0.5h,且位置固定解较之于浮点解的精度增益有限[21],影响了PPP 模糊度固定算法在高精度GPS定位中的普适性.
借鉴网络实时动态定位(Network-based Real Time Kinematic,NRTK)的技术方案[23-24],文献[19, 25]均提出了克服上述第二条缺陷的方法,具体思路为:利用局域增强参考站网,并通过固定IGS 卫星轨道和钟差,以及事先获取的SPBs,从不同的GPS相位组合观测值中分离电离层和对流层等两类大气延迟,并随后时空内插(预报)至PPP 用户站,实现了100km 区域内的单历元PPP 模糊度固定.本文从理论算法和实际应用等两方面出发,探索一种能实现更大区域内PPP 模糊度快速固定的新方案,其主要技术特点包括:(1)SPBs独立可估,其动态模型可选取为较为合理的随机游走过程(Random Walk Process),以避免非整法中将其强制约束为时不变参数所引起的可靠性降低等问题,也可避免去耦法采用白噪声所引起的待估参数增多,估值精度不高;(2)联合处理参考网的非差、非组合GPS观测值,考虑已知的卫星、参考站坐标和卫星钟差,并通过固定一组独立的双差整周模糊度,同步获取基准一致的SPBs和电离层延迟,避免文献[19]的分步处理策略,以及由此引起的不同类改正信息间的不一致性;(3)PPP处理中,分别考察了参考网内、外的电离层内插、外推精度以及动态PPP模式下的模糊度固定效果.
文中首先介绍了参考网和PPP 各自的数据处理方法,重点分析网数据处理中,部分线性相关的参数(如卫星和接收机的相位偏差、电离层、硬件延迟等)所引起的观测方程列秩亏现象,以及消除秩亏的策略;随后,基于两类网解改正信息(SPBs和电离层延迟),导出了PPP模糊度固定的具体实施方案.最后,采用华北某参考站网进行试验,考察了网解SPBs的时间稳定性、以及电离层延迟的内插和外推效果等;分别对参考网内外的两测站实施仿动态PPP,通过分析模糊度固定时长、定位精度的改善等,验证了算法的总体有效性.
2 数据处理方法 2.1 网数据处理忽略多路径效应、高阶电离层延迟[26]等误差,GPS伪距和相位方程可联合表示为[25]:
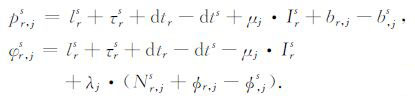
|
(1) |
其中,pr,js和φ r,js为测站r至卫星s第j个频率的伪距和相位观测值(单位:m);lrs为站星距;τrs为对流层斜延迟;dtr和br,j为接收机的钟差和硬件延迟; dts和b,js为卫星的钟差和硬件延迟;Irs为L1 频率上的电离层群延迟;μj,λj2 /λ12为电离层弥散系数;λj为频率j测距信号的波长;Nr,js、Φr,j和Φ ,js为非差整周模糊度、接收机和卫星的相位偏差(单位均为周(cycle)).
为简化公式推导,且不失一般性,网数据处理中假定:
(1) n个参考站(r=1,…,n)同步观测m颗GPS卫星(s=1,…,m)的双频(j=1,2)观测值;
(2) 各参考站的坐标Pr= (Xr Yr Zr) T 先验已知;
(3) 各GPS卫星的坐标Qs= ( Xs Ys Zs)T 和钟差dts可分别由IGS精密星历和钟差产品内插得到,且
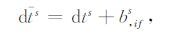
|
(2) |
其中,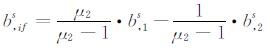
(4) τrs可被重新参数化为τrs=Frs·Tr,其中Frs和tr分别为投影函数和天顶对流层延迟[5].
式(1)中的若干类参数之间存在线性相关性,由此可引起观测方程的列秩亏以及参数估值的不唯一性[27-28].现简要介绍线性相关的参数类型及所采用的分步消秩亏策略:
第一步 式(1)伪距方程中,dtr-dts和μj·Irs项均与br,j-b,js之间存在线性相关.考虑br,j-b,js可被等价地表示为
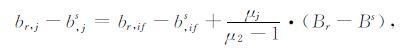
|
(3) |
其中,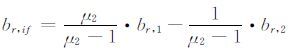
显见,br,j-b,js被分解为三个部分:br,if,bifs,和(Br-Bs),且可分别被dtr,dts和μj·Irs吸收,由此形成如下三类新参数:
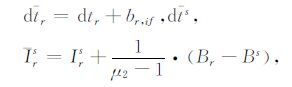
|
(4) |
第二步 对于式(1)的相位方程,需将其中的dtr,dts和μj·Irs重新参数化为式(4)中的dtr,dts和μj·Irs形式,以确保伪距和相位方程中的公共未知参数具备一致的形式.即,
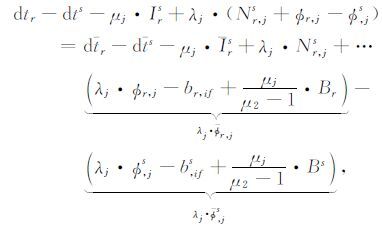
|
(5) |
第三步 式(5)中,Nr,js、Φr,j和Φ ,js三类参数依然线性相关,可通过将Φv,j、N1…n,jw和Nv,j1…m等共n+ m个参数选取为基准[27]加以消除,下标v代表某接收机(基准站),上标w代表某卫星(基准星).此时,
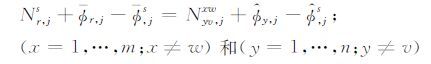
|
(6) |
显见,该消秩亏过程可形成2(n-1)(m-1)个双差模糊度Nyv,jxw和2m个独立可估的双频SPBs(即
综合上述推导,对应于式(1)的满秩观测方程为
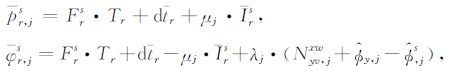
|
(7) |
式中,pr,js和φ r,js分别为修正了已知站星距和卫星钟差的伪距和相位观测值.
网数据处理采用联合正、反向卡尔曼滤波的参数估计方案,具体设置为:式(7)观测方程中,截止高度角选取为5°,并采用高度角加权策略,天顶方向伪距和相位观测值的中误差经验选取为3dm 和3mm;状态模型中,每2h 估计一组Tr;Irs、
PPP模糊度固定所需的网解改正信息包括
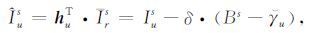
|
(8) |
其中,hu为n×1的内插向量,且满足hu·en=1,以确保卫星仪器偏差Bs不受内插过程影响;
经由近似站星距lu,0s、dtIs、
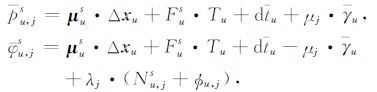
|
(9) |
其中各项符号的含义与式(7)中的对应项类似,但下标u此时对应PPP用户.此外,μus为u-s方向的单位矢量;Δxu为用户u近似位置xu,0 的改正数;γu为接收机仪器偏差,但吸收了
将某卫星选取为基准星(如w),经由星间单差,式(9)可被等价地转化为
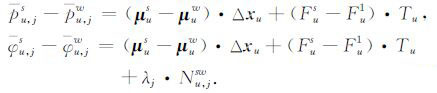
|
(10) |
显见,式(10)中的电离层延迟已被显著削弱,且待估模糊度参数Nu,jsw已具备整数特性,PPP 模糊度的快速固定由此成为可能.本文算法的具体流程如图 1所示.
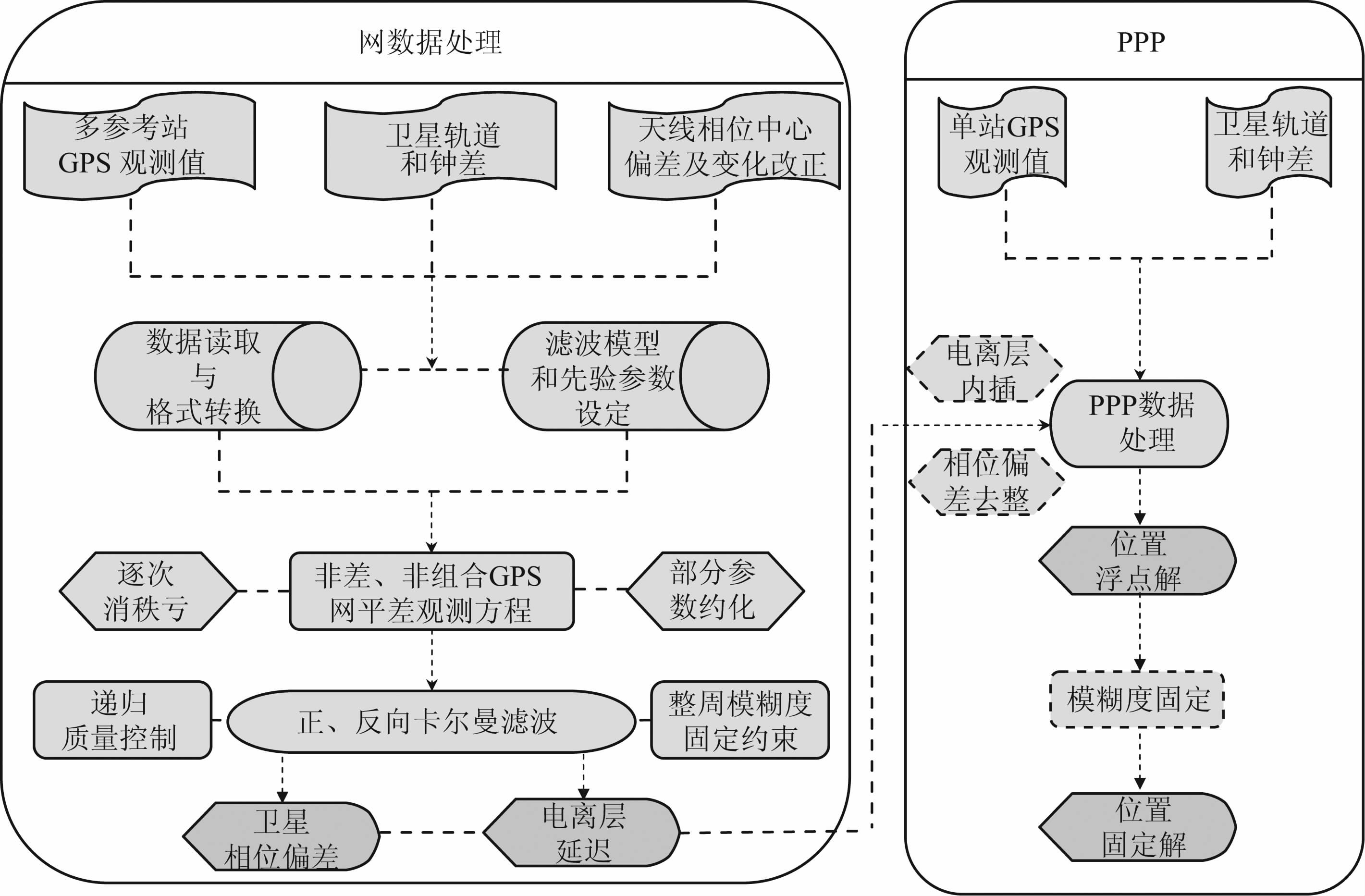
|
图 1 本文算法流程图 Fig. 1 Flowchart of the method proposed in this paper |
实验基于华北某省CORS(连续运行参考系统) 的双频GPS数据,各测站的空间分布如图 2 所示,其中,SJJZ和XTLX 被用作PPP 用户站,其余作为参考站.观测时段为2009年第220天(UTC),采样间隔为30s.在随后的论述中,将分别给出参考网和PPP的具体数据处理策略,并对相应的实验结果进行分析.
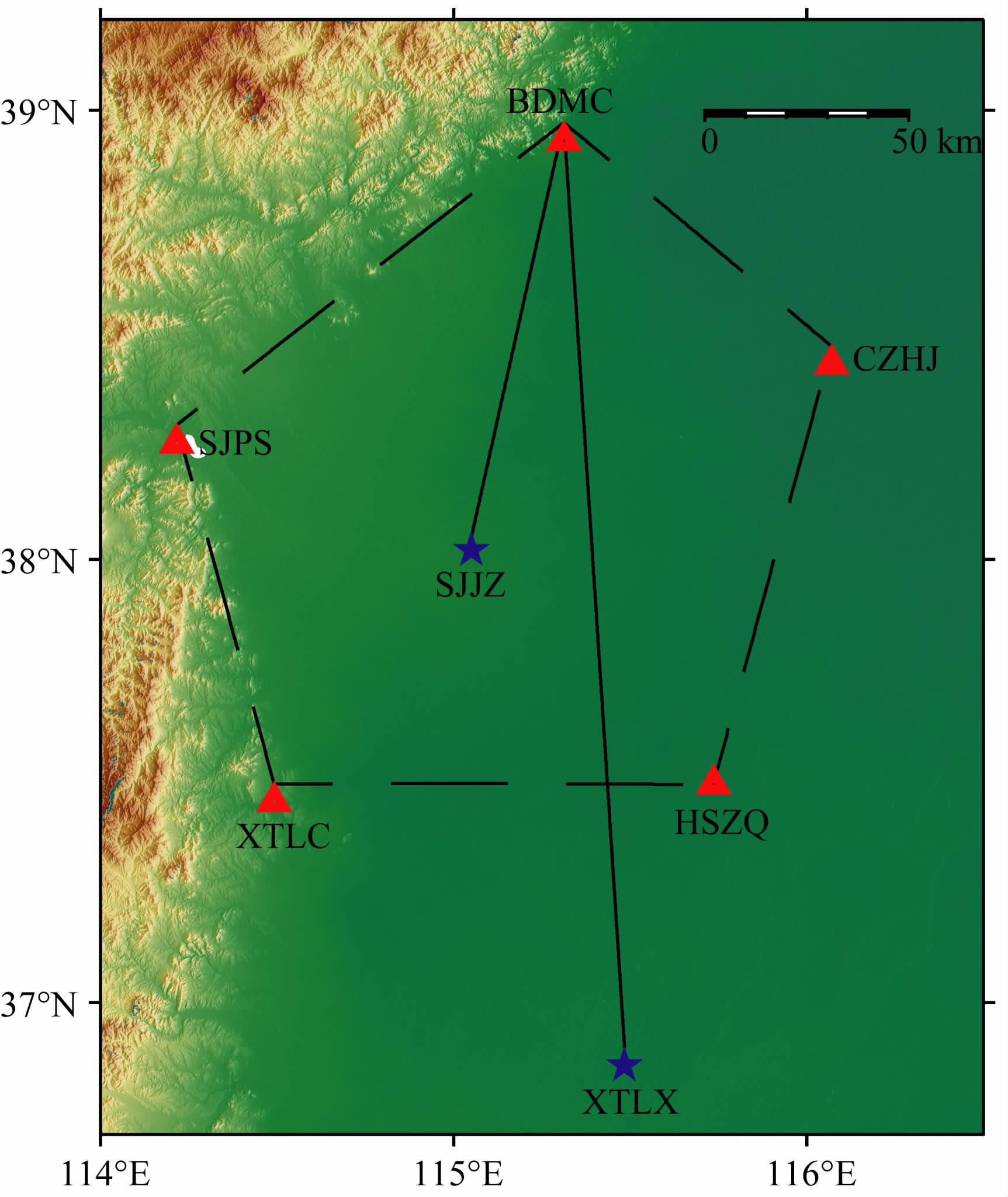
|
图 2 华北某CORS的测站分布图SJJZ和XTLX 为仿PPP用户站,其余用作参考站. Fig. 2 The configuration of CORS in northern China SJJZ & XTLX are assigned as simulated PPP users, and the remaining sitesare used asreference stations. |
图 3a表示网处理中,整周模糊度固定的ratio 检验结果.由于各历元的浮点模糊度估值均为全局最优的平滑解(正、反向滤波解的加权平均),其精度较高,对应的ratio检验值(最优与次优整周模糊度候选值的残差二范数之比)均小于其临界值,表明模糊度固定的成功率为100%;图 3b表示单天内共视卫星数的变化.综合对比图(a,b)可知,ratio检验值与卫星数之间的变化存在较强的相关性[29]:以3(a,b)黑色虚线内的细节部分为例(具体放大图分别为(c)和(d)),对于卫星数不变的观测时段,各历元的浮点模糊度精度、维数相同,故ratio检验值在该时段内保持不变,而当卫星出现升降时,模糊度维数改变,由此导致了对应的ratio检验值发生变化.
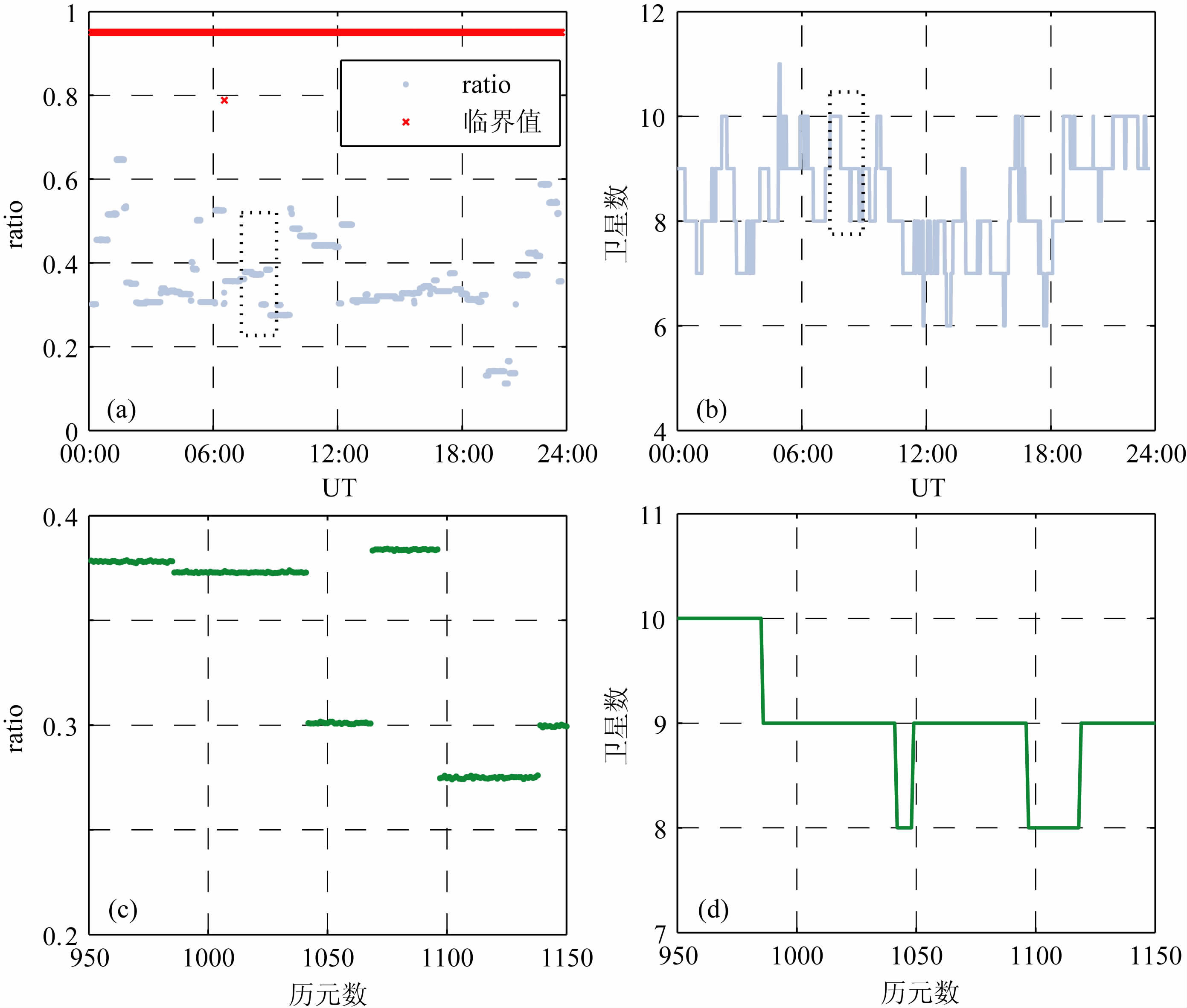
|
图 3 CORS 网模糊度解算结果(a)和(b)为ratio检验结果和可视卫星数;(c)和(d)分别对应(a)和(b)中黑色虚线内的细节部分 Fig. 3 Results of ambiguity resolution in CORS network processing (a) and (b) are the ratio test results and the numbers of visible satellites; (c) and (d) correspond respectively to the local features of (a) and (b) that are labeled out within dotted lines |
图 4中(a,b)分别表示L1和L2频率SPBs的模糊度固定解,整数部分已事先移除,以便于考察其时变性.由图中结果可知,对于每一个连续的卫星弧段(图中不同的颜色代表不同的卫星),双频SPBs 估值的历元间变化十分平稳,约为0.1~0.2 周,其中,存在显著变化的时段均为各弧段的起止时刻,原因在于此时的卫星高度角过低,相应的估值更易受各种非模型化误差(如观测噪声,多路径效应等)的影响.
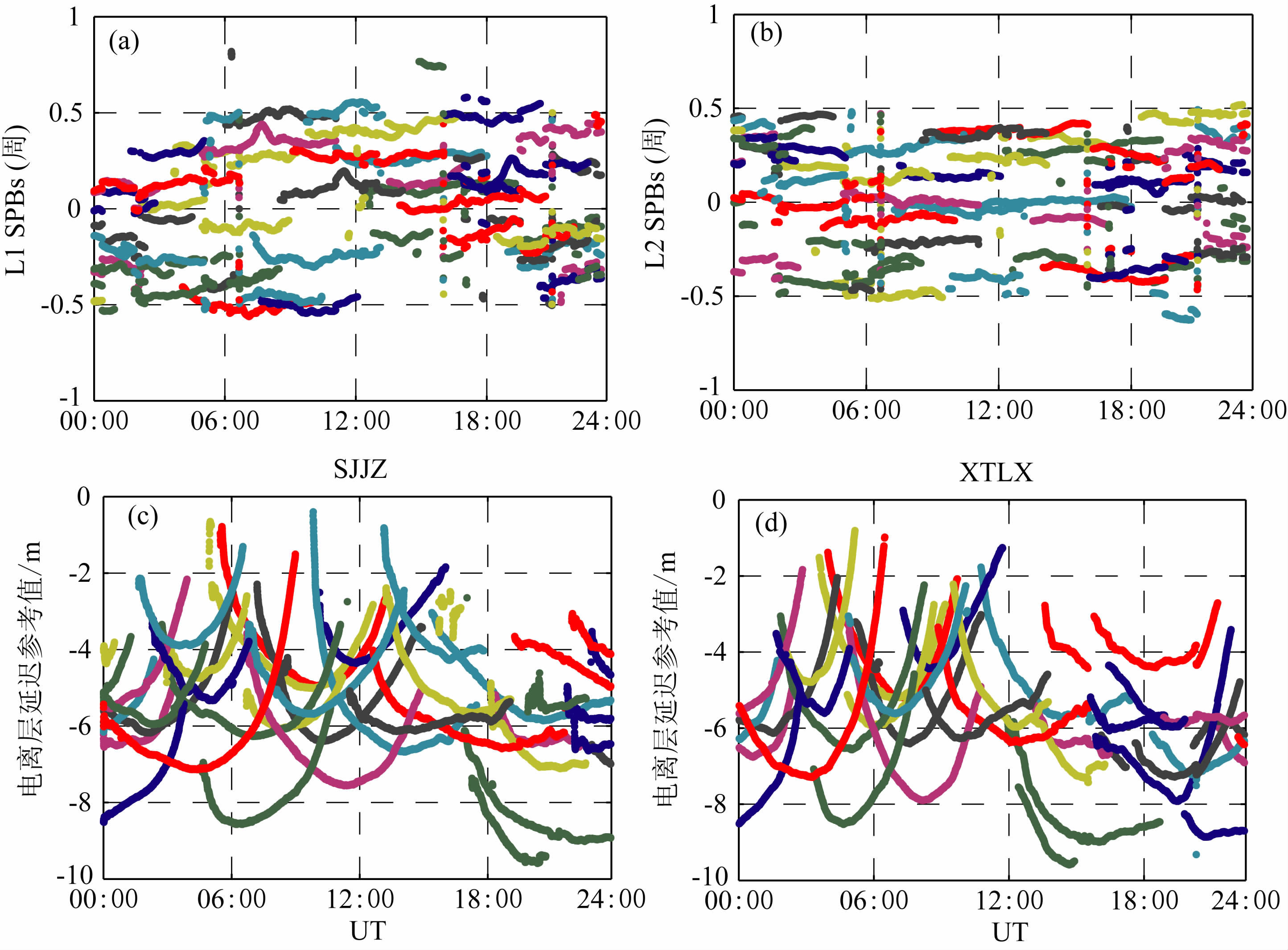
|
图 4 (a)和(b)L1和L2频率的SPBs估值;(c)和(d)SJJZ和XTLX 处的电离层延迟参考值 Fig. 4 Panels (a) and (b) : SPBs on L1 and L2 frequencies; (c) and (d) : reference values of ionospheric delays at SJJZ and XTLX: different colors correspond to different satellites |
此外,联合处理图 2中所有测站的双频数据,经由整周模糊度固定后,可得SJJZ 和XTLX 处的电离层延迟估值,如图 4 中(c,d)所示.由于该延迟中包含了接收机和卫星的仪器偏差(见式(4)),故存在一定量的负值.将该电离层延迟估值作为参考值,并分别与SJJZ 和XTLX 处的内插和外推值(见图 5 (a,b))作差比较,用于衡量电离层的内插效果,对应的结果如图 5(c,d)所示.其中,除内插误差外,该结果中还分别包含了SJJZ 和XTLX 接收机仪器偏差(即式(9)中的γu)的影响.由于γu与卫星无关,若内插或外推过程不包含误差影响,则不同卫星的结果将完全重合.因此,不同卫星内插或外推结果的离散程度,即可用于量化内插误差的量级[6].各卫星弧段间的结果差异最大可达0.2 dm,由此引起0.2/2=0.1dm的内插或外推误差(误差显著性水平取为95%,此时极限误差等于2倍中误差).
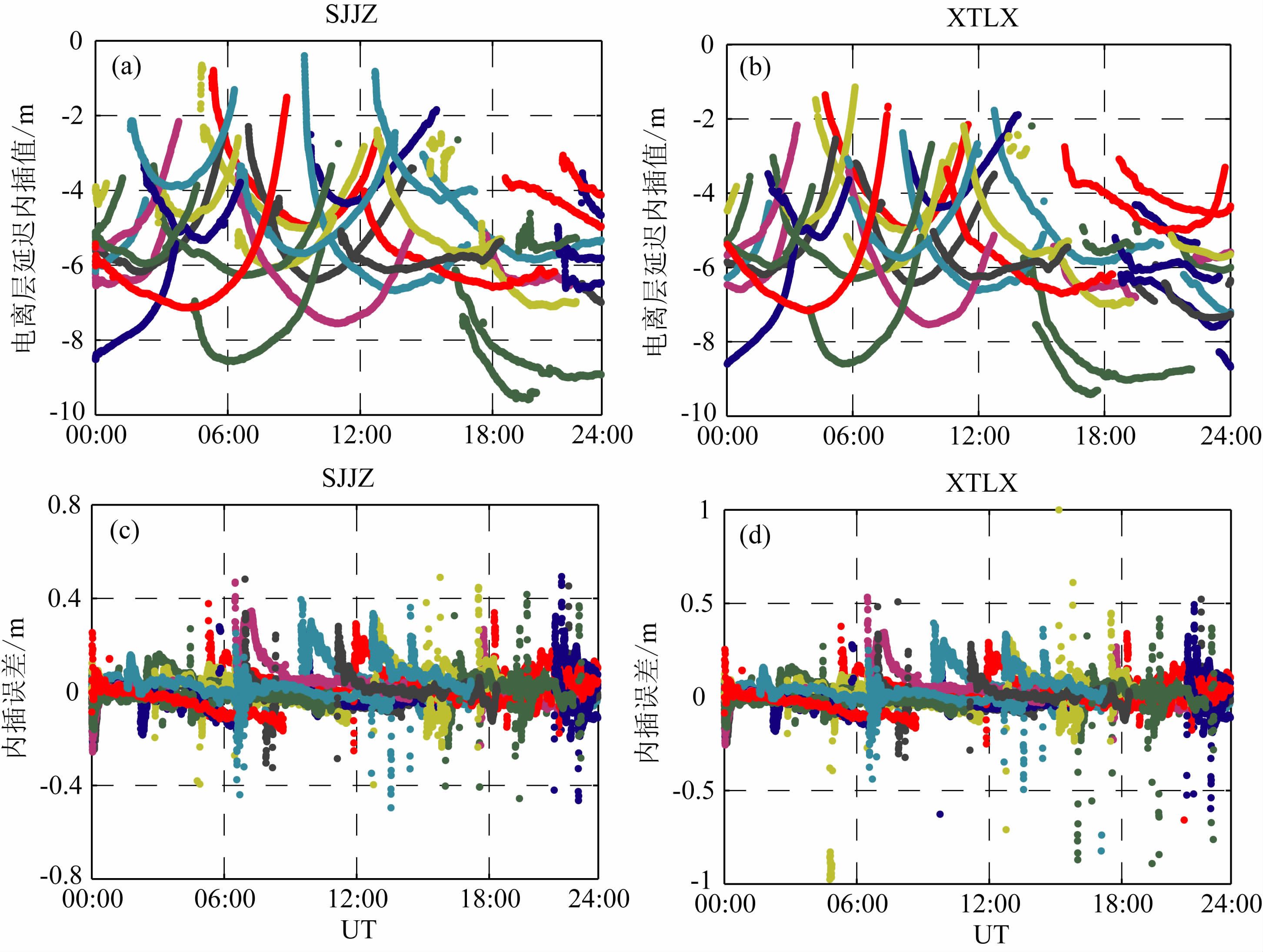
|
图 5 SJJZ和XTLX 处电离层延迟内插值及相应的内插误差 Fig. 5 Interpolated ionospheric delays at both sites of SJJZ and XTLX and the corresponding interpolation errors |
为验证PPP整周模糊度固定的效率,以及模糊度固定对于定位结果的影响,现设计如下的实验方案:基于SJJZ和XTLX 测站的双频观测值(已采用CORS网解改正数以及IGS轨道和钟差改正),自不同的起算历元(此处假定为i=1,2,…)滤波实施PPP,计算模糊度可被准确时所需历元数(此处假定为k),即为自历元i始PPP 模糊度固定所需时长,两测站对应的结果如图 6(a,c)所示,6(b,d)则列出了模糊度固定时刻的ratio检验结果.在滤波实施的过程中,测站位置选取为白噪声过程(即仿动态处理),其余参数的估计策略与网处理过程相同,此处不再详述.
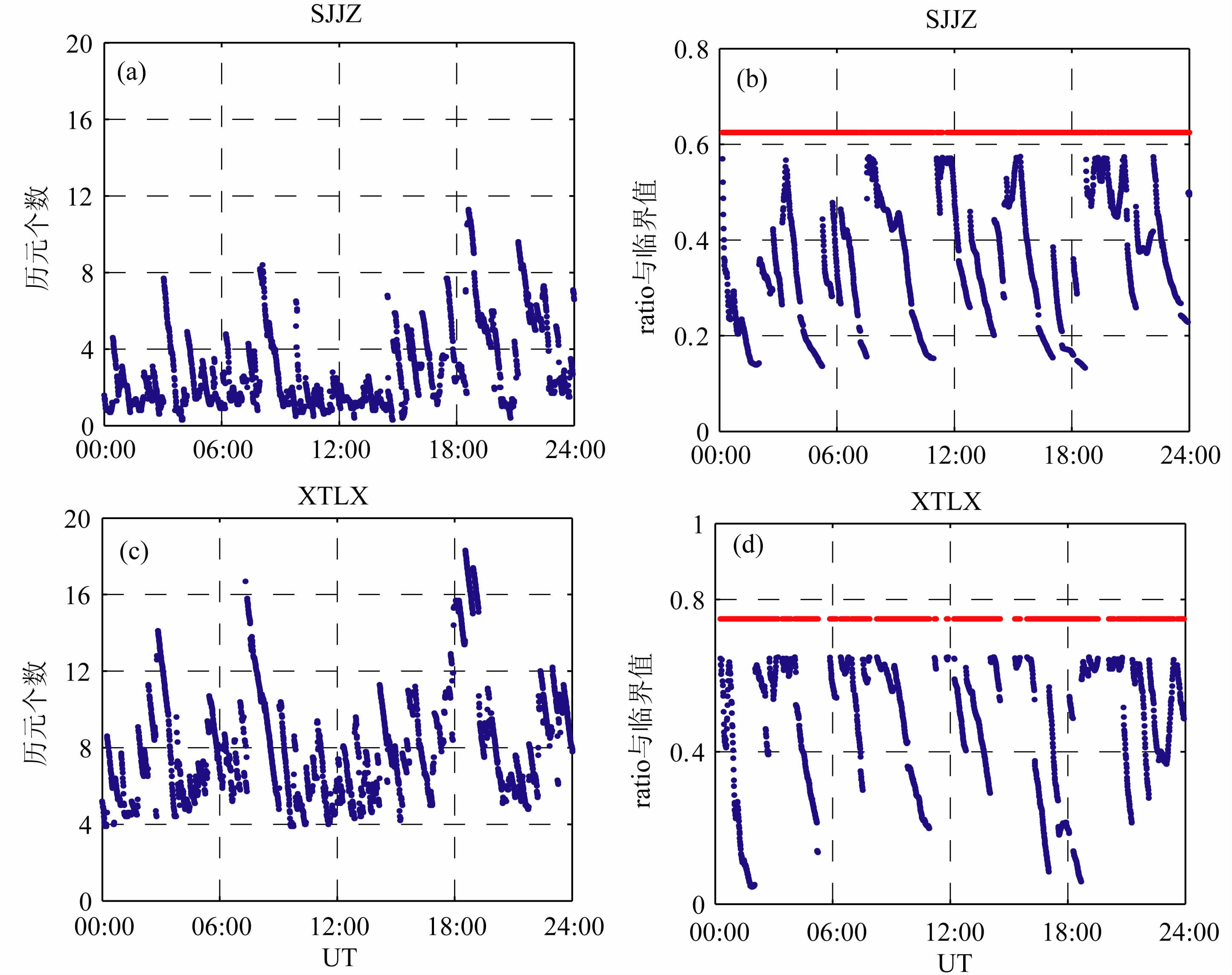
|
图 6 (a,c)单天内不同时刻固定PPP模糊度所需历元数;(b,d)模糊度固定时刻的ratio检验结果 Fig. 6 (a,c) Numbers of epochs which are necessary for PPP ambiguity resolution within a day; (b,d)Ratio test results at the epochs with successful ambiguity resolution |
由图 6可知,单天内任意时刻起算,固定仿动态PPP 的整周模糊度所需的历元个数均不超过20 (10min),大部分时刻(约95%)所需的历元个数仅为2(1 min).16∶00-18∶00(UT)时段内,PPP 模糊度固定所需历元个数较之其余时段偏多,原因可能在于此期间内较少的卫星数和频繁的卫星升降(见图 3b).图 7中给出了SJJZ和XTLX 的PPP 定位结果:横轴表示历元时刻i=1,2,…,纵轴则对应于i+k时刻三维(NEU)位置解误差(与已知的参考值比较),图 6(a,c)为XTLX 和SJJZ的位置浮点解误差,(b,d)为相应的固定解误差.显见,PPP 模糊度固定前后,定位误差存在量级上的差异,以SJJZ 的定位结果为例,定位精度(RMS)从2.6,3.7dm 和3.0dm(NEU)提高至4.4,5.9cm 和6.5cm,改善程度约为80% ~85%,证明了本文算法在加速PPP模糊度固定和提高定位精度方面的双重有效性.
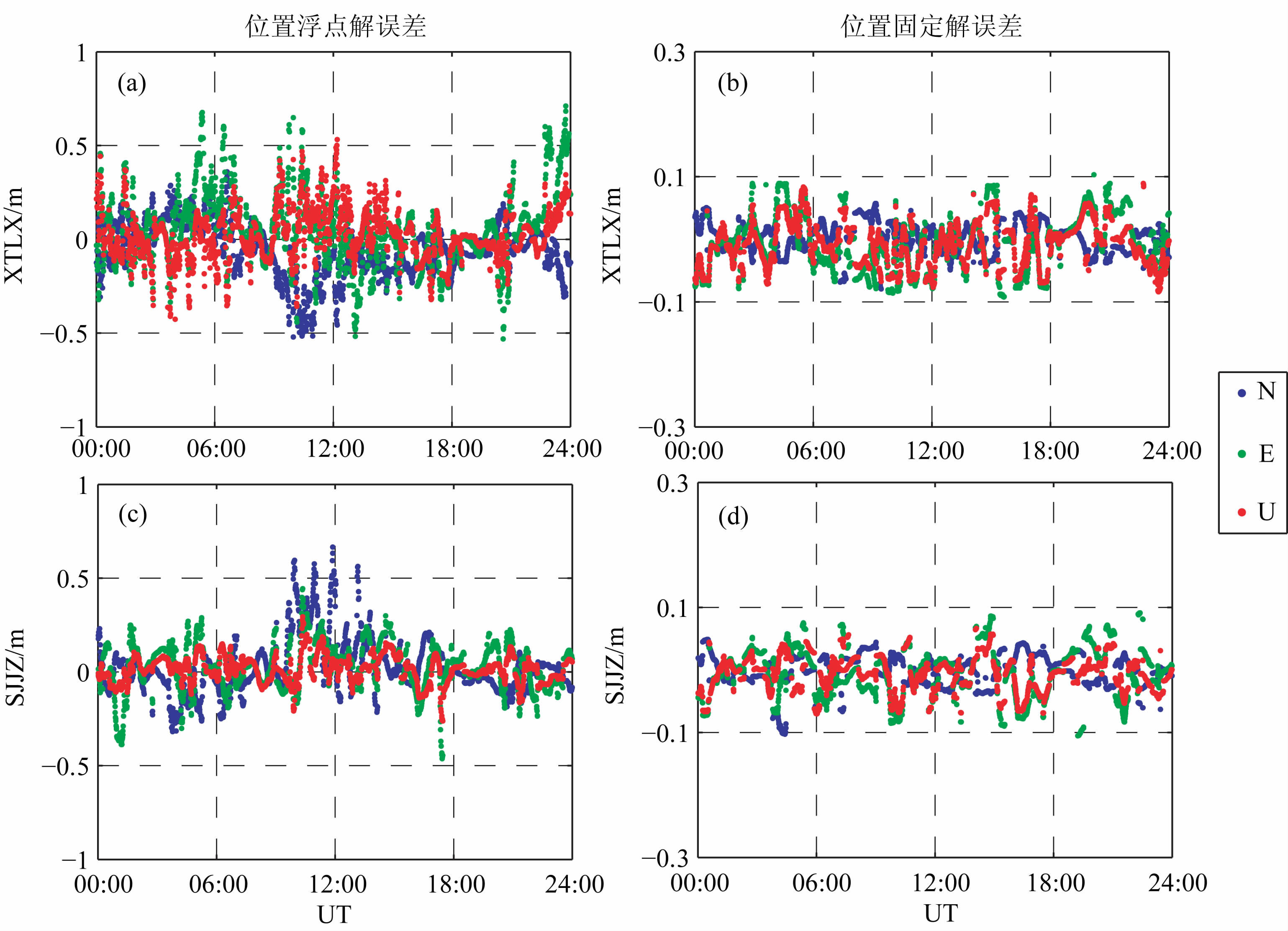
|
图 7 PPP模糊度固定前后三维位置解(NEU)误差(a,c)XTLX 和SJJZ处的浮点解;(b,d)XTLX 和SJJZ处的固定解. Fig. 7 NEU positioning errors before and after ambiguity resolution in PPP (a,c) Ambiguity-float solutions of XTLX & SJJZ; (b,d) Ambiguity-fixed solutions of XTLX & SJJZ. |
本文介绍利用区域GPS网分离高精度的SPBs 和电离层延迟,以实现PPP整周模糊度快速固定的算法.经由实测CORS数据检验,考察了SPBs的时间稳定性、电离层内插和外推精度以及PPP 模糊度固定的效率和定位解改善等.实验结果表明:双频SPBs随时间变化较为稳定,各连续弧段内的变化不超过0.2周;站间距为100~200km 的CORS网内外,电离层内插和外推误差均小于1dm,使得PPP 模糊度固定在绝大部分时刻仅需2 个历元,三维位置固定解较之浮点解的精度改善可达80%~85%.
本文算法中依然存在若干待深入研究的细节问题,具体包括:(1)考虑到本文算例中各CORS站之间的高程差异过大(部分测站,如BDMC 和XTLC 之间高差达2.4km),故PPP 数据处理中,未采用内插的对流层延迟改正,以避免可能的较严重对流层内插误差影响[29].因此,当各参考站之间存在较大高差时,如何选取有效的对流层内插函数,以充分利用网解的全部改正信息,值得深入分析;(2)在CORS网和PPP 数据处理过程中,SPBs的状态模型均选取为随机游走过程,且采用不同的功率谱密度值,上述模型化方案均为经验选取,部分时刻可能难以描述其真实的时变特性,故需对其有效性实施更为深入的检验.
| [1] | Zumberge J, Heflin M, Jefferson D, et al. Precise point positioning for the efficient and robust analysis of GPS data from large networks. J. Geophys. Res. , 1997, 102(B3): 5005-5017. DOI:10.1029/96JB03860 |
| [2] | Kouba J, Heroux H. Precise point positioning using IGS orbit and clock products. GPS Solut , 2001, 5(2): 12-28. DOI:10.1007/PL00012883 |
| [3] | 张小红, 刘经南, ForsbergR. 基于精密单点定位技术的航空测量应用实践. 武汉大学学报 (信息科学版) , 2006, 31(1): 19–22. Zhang X H, Liu J N, Forsberg R. Application of precise point positioning in airborne survey. Geomat. Inf. Sci. Wuhan Univ. (in Chinese) (in Chinese) , 2006, 31(1): 19-22. |
| [4] | 刘经南, 叶世榕. GPS非差相位精密单点定位技术探讨. 武汉大学学报 (信息科学版) , 2002, 27(3): 234–240. Liu J N, Ye S R. GPS Precise point positioning using undifferenced phase observation. Geomat. Inf. Sci. Wuhan Univ. (in Chinese) (in Chinese) , 2002, 27(3): 234-240. |
| [5] | 张宝成, 欧吉坤, 袁运斌, 等. 基于GPS双频原始观测值的精密单点定位算法及应用. 测绘学报 , 2010, 39(5): 478–483. Zhang B C, Ou J K, Yuan Y B, et al. Precise point positioning (PPP) algorithm based on original dual-frequency GPS code and carrier-phase observations and its application. Acta Geodaetica et Cartographica Sinica (in Chinese) (in Chinese) , 2010, 39(5): 478-483. |
| [6] | 张宝成, 欧吉坤, 李子申, 等. 利用精密单点定位求解电离层延迟. 地球物理学报 , 2011, 54(4): 950–957. Zhang B C, Ou J K, Li Z S, et al. Determination of Ionospheric Observables with Precise Point Positioning. Chinese J. Geophys. (in Chinese) (in Chinese) , 2011, 54(4): 950-957. |
| [7] | Soycan M, Ata E. Precise point positioning versus traditional solution for GNSS networks. Sci. Res. Essays , 2011, 6(4): 799-808. |
| [8] | Blewitt G. Carrier phase ambiguity resolution for the global positioning system applied to geodetic baselines up to 2000 km. J. Geophys. Res. , 1989, 94(B8): 10187-10203. DOI:10.1029/JB094iB08p10187 |
| [9] | Bisnath S, Gao Y. Current state of precise point positioning and future prospects and limitations. // Sideris M G ed. Observing Our Changing Earth. New York: Springer, 2007: 615-623. |
| [10] | Ge M, Gendt G, Rothacher M, et al. Resolution of GPS carrier-phase ambiguities in precise point positioning (PPP) with daily observations. J. Geodesy , 2008, 82(7): 389-399. DOI:10.1007/s00190-007-0187-4 |
| [11] | Bertiger W, Desai S D, Haines B, et al. Single receiver phase ambiguity resolution with GPS data. J. Geodesy , 2010, 84(5): 327-337. DOI:10.1007/s00190-010-0371-9 |
| [12] | Hauschild A, Montenbruck O. Kalman-filter-based GPS clock estimation for near real-time positioning. GPS Solut , 2008, 13(3): 173-182. |
| [13] | 张小红, 李星星, 郭斐, 等. 基于服务系统的实时精密单点定位技术及应用研究. 地球物理学报 , 2010, 53(6): 1308–1314. Zhang X H, Li X X, Guo F, et al. Sever-based real-time precise point positioning and its application. Chinese J. Geophys. (in Chinese) (in Chinese) , 2010, 53(6): 1308-1314. |
| [14] | 李浩军, 王解先, 陈俊平, 等. 基于GNSS网络的实时精密单点定位及精度分析. 地球物理学报 , 2010, 53(6): 1302–1307. Li H J, Wang J X, Chen J P, et al. The realization and analysis of GNSS network based real-time precise point positioning. Chinese J. Geophys. (in Chinese) (in Chinese) , 2010, 53(6): 1302-1307. |
| [15] | Geng J, Meng X, Dodson A H, et al. Integer ambiguity resolution in precise point positioning: method comparison. J. Geodesy , 2010, 84(9): 569-581. DOI:10.1007/s00190-010-0399-x |
| [16] | Collins P, Bisnath S, Lahaye F, et al. Undifferenced GPS ambiguity resolution using the decoupled clock model and ambiguity datum fixing. Navigation , 2010, 57(2): 123-135. DOI:10.1002/navi.2010.57.issue-2 |
| [17] | Geng J, Teferle F N, Shi C, et al. Ambiguity resolution in precise point positioning with hourly data. GPS Solut , 2009, 13(4): 263-270. DOI:10.1007/s10291-009-0119-2 |
| [18] | 张小红, 李星星. 非差模糊度整数固定解PPP新方法及实验. 武汉大学学报 (信息科学版) , 2010, 35(6): 657–660. Zhang X H and Li X X. A new method for zero2Differenced integer ambiguity resolution and its application to PPP. Geomat. Inf. Sci. Wuhan Univ. (in Chinese) (in Chinese) , 2010, 35(6): 657-660. |
| [19] | Li X, Zhang X, Ge M. Regional reference network augmented precise point positioning for instantaneous ambiguity resolution. J. Geodesy , 2010, 85(3): 151-158. |
| [20] | Geng J, Meng X, Dodson A H, et al. Rapid re-convergences to ambiguity-fixed solutions in precise point positioning. J. Geodesy , 2010, 84(12): 705-714. DOI:10.1007/s00190-010-0404-4 |
| [21] | Laurichesse D, Mercier F, Berthias J P, et al. Integer ambiguity resolution on undifferenced GPS phase measurements and its application to PPP and satellite precise orbit determination. Navigation , 2009, 56(2): 135-149. DOI:10.1002/navi.2009.56.issue-2 |
| [22] | Collins P. Decoupled clock model with ambiguity datum fixing. US Patent, 2010, No.: US 2010/0188285 A1. |
| [23] | 周乐韬, 黄丁发, 袁林果, 等. 网络RTK参考站间模糊度动态解算的卡尔曼滤波算法研究. 测绘学报 , 2008, 36(1): 37–42. Zhou L T, Huang D F, Yuan L G, et al. A kalman filtering algorithm for online integer ambiguity resolution in reference station network. Acta Geodaetica et Cartographica Sinica (in Chinese) (in Chinese) , 2008, 36(1): 37-42. |
| [24] | 高星伟, 刘经南, 葛茂荣. 网络RTK基准站基线的单历元模糊度的搜索方法. 测绘学报 , 2002, 31(4): 305–309. Gao X W, Liu J N, Ge M R. An ambiguity searching method for network RTK baselines between base stations at single epoch. Acta Geodaetica et Cartographica Sinica (in Chinese) (in Chinese) , 2002, 31(4): 305-309. |
| [25] | Teunissen P J G, Odijk D, Zhang B C. PPP-RTK: results of CORS network-based PPP with integer ambiguity resolution. J. Aero. Astron. Aviat , 2010, 42(4): 223-230. |
| [26] | Liu X F, Yuan Y B, Huo X L, et al. A model analysis method on the effect of second-order ionospheric delay on GPS positioning. Chinese Sci. Bull. , 2010, 55(15): 1529-1534. DOI:10.1007/s11434-010-3070-2 |
| [27] | Teunissen P J G. Generalized inverses, adjustment, the datum problem and S-transformations. // Grafarend E W, Sanso F, eds. Optimization and Design of Geodetic Networks. Berlin: Springer, 1985, 11-55. |
| [28] | 欧吉坤. 测量平差中不适定问题的统一表达与选权拟合法. 测绘学报 , 2004, 33(4): 283–288. Ou J K. Uniform expression of solutions of ill-posed problems in surveying adjustment and the fitting method by selection of the parameter weights. Acta Geodaetica et Cartographica Sinica (in Chinese) (in Chinese) , 2004, 33(4): 283-288. |
| [29] | Teunissen P J G. The least-square ambiguity decorrelation adjustment: a method for fast GPS integer ambiguity resolution. J. Geodesy , 1995, 70(1-2): 65-82. DOI:10.1007/BF00863419 |
| [30] | Teunissen P J G, Verhagen S. The GNSS ambiguity ratio-test revisited: a better way of using it. Surv. Rev. , 2009, 41(312): 138-151. DOI:10.1179/003962609X390058 |
| [31] | Wu S Q, Zhang K F, Yuan Y B, et al. Spatio-temporal characteristics of the ionospheric TEC variation for GPSnet-based real-time positioning in Victoria. J. Global Positioning Syst. , 2006, 5(1-2): 52-57. |
| [32] | Jarlemark P O J, Emardson T R. Strategies for spatial and temporal extrapolation and interpolation of wet delay. J. Geodesy , 1998, 72(6): 350-355. DOI:10.1007/s001900050174 |
 2012, Vol. 55
2012, Vol. 55

