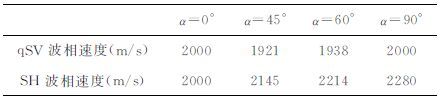井周介质的各向异性是石油测井中经常遇到的问题,这给测井解释提出了新的要求.由于沉积作用和构造应力的影响最常遇到的各向异性地层是横向各向同性(TI)介质.对TI地层主轴与井轴呈两种典型夹角的声波测井问题,已开展了大量的研究工作.一种是对称轴竖直的TI(VTI)介质,介质对称主轴与井轴平行,体系仍保持井轴对称性,井孔声场有解析解,20世纪80年代末以来,对这种情况研究的最为详尽.另一种是对称轴水平的TI(HTI)介质,介质对称主轴与井轴垂直,体系不再具有井轴对称性,场方程不能解析求解.由于这种情况体系仍保持轴向均匀性,本质上是平面内二维不对称,对此,研究者们先后提出了两种摄动处理方法[1~3]和若干二维有限差分数值模拟方法[4~7],这些工作为多极声测井地层各向异性判断和异常地应力预测提供了理论依据和处理手段.然而实际的横向各向同性地层的主轴并不总是与井轴平行或垂直,而常常是有一定倾角,特别是随着大斜度井(和水平井)数量的迅速增加,这种情况变的更为多见.基于直井建立的传统测井解释方法在斜井中遇到诸多不适应,其中各向异性最为突出.由于各向异性地层倾斜井孔体系轴向均匀性进一步破坏,场方程只能用三维的数值方法求解.近年国内外都开展了针对这一问题的研究工作[8~12],方法不尽相同.建立起各向异性地层斜井多极声测井的数值模拟方法是解决大斜度井和水平井测井解释的基本条件,具有重要意义.本文是在马俊等(2002)[8]提出的处理框架基础上,采用三维二阶精度交错网格应力-速度有限差方法,通过改进井轴上场点奇异性与内边界处理以及应用 Liao的吸收边界条件[13]来使计算精度达到正确显示弱信号的要求[11],数值模拟了与横向各向同性(TI)介质对称主轴成任意角度(倾斜角)的井孔中正交偶极子声源激发的非轴对称声场,着重数值考察各种倾斜角下沿井传播的不同偏振弯曲波分裂现象.
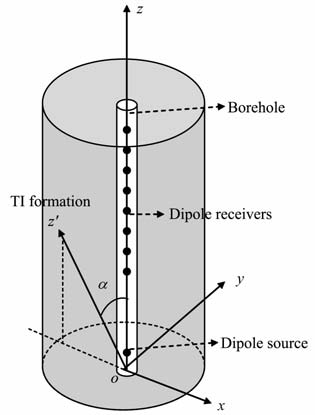
2 理论模型与公式本文以TI介质包围的倾斜井孔为研究对象,井轴与介质的对称主轴的夹角为任意角度α,它等价于介质对称主轴相对井孔倾斜的情况,图 1 为理论模型示意图.本文采用柱坐标系下三维应力速度有限差分,柱坐标系的z轴与井轴重合.下面推导柱坐标系下TI介质主轴z′ 与z轴成任意角度情况下的应力-应变关系.由于TI介质的性质,在与介质对称主轴垂直的平面内传播的波是各向同性的,因此在井孔倾斜的情况下,所研究的问题与z′ 轴在oxy平面内的方向角无关,本文取z′ 轴在oxy平面内的投影与x轴负向重合.
|
图 1 理论模型示意图 Fig. 1 Schematic diagram of theoretical model |
横向各向同性介质由5个基本常数A,C,L,F,N确定,在直角坐标系(x,y,z)中当介质对称主轴z′ 与z轴重合时,弹性系数矩阵为

|
(1) |
将介质对称轴绕y轴旋转-α,则介质弹性常数矩阵变为C1 =MC0MT,M为变换矩阵,MT 为M的转置矩阵.M的具体形式如下:
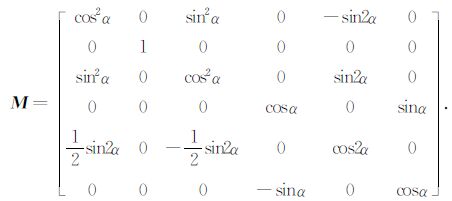
|
(2) |
将直角坐标系中的弹性系数矩阵变换到柱坐标系(r,θ,z)中就得到柱坐标系下的各向异性介质弹性系数矩阵C′ = M′C1M′T.变换矩阵M′ 为
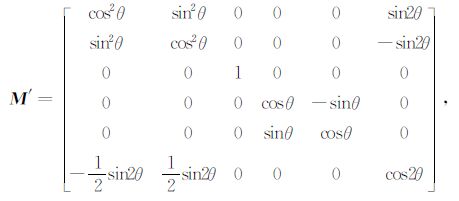
|
(3) |
C′ = {c′ij}仍为对称矩阵.通过C′ 即可得到介质主轴与井轴成任意角度情况下的应力-应变关系,并进而得到应力张量各分量时间导数的方程

|
(4) |
式中${{\dot{T}}_{\mu v}}$ 表示Tμν(μ,ν=r,θ,z)对时间的一阶导数,
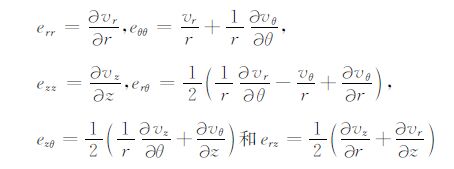
|
分别为应变张量各分量对时间的一阶导数(应变率).其中gμν(μ,ν =r,θ,z)是应力源.速度的分量方程为
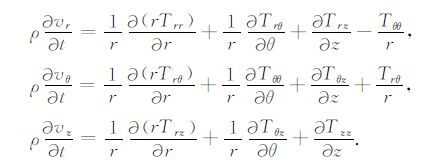
|
(5) |
本文在数值模拟中,使用定声压正交偶极源,即
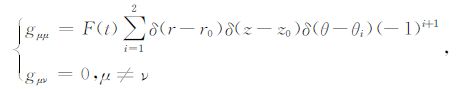
|
(6) |
其中r0 为偶极元半径,z0 为偶极元空间位置,对x方向偶极子θ1 = 0,θ2 = π,对y方向偶极子θ1 =π/2,θ2 =3π/2,声源时域脉冲为瑞克子波F(t)=∫0t4α2t2e-αtsinω0tdt,式中ω0 为声源中心角频率,α=ω0/$\sqrt{3}$.(4)式和(5)式构成井外介质波动方程.
3 速度场、应力场在交错网格上的离散化采用柱坐标系下有限差分交错网格[5],将速度场和应力场分配在各网格点上.根据交错网格算法,三个法向应力位于三维整数网格线节点上,而其他各应力分量及速度分量,在其角标对应方向上位于半整数离散点上,在其角标中未出现的方向上位于整数离散点上.假设计算模型的空间范围是0 ≤r≤rmax, 0≤θ≤2π,0≤z≤zmax, 离散化为jmax×lmax×kmax 个单元.按交错网格算法,各未知场量按照如下方式在空间和时间域采样:

|
其中rj=jΔr,θl=lΔθ,zk=kΔz,tn=nΔt,Δr,Δθ,Δz分别为网格在三个方向上的空间步长,Δt为时间步长.本文采用时空交错网格上二阶精度的中心差分[14].为了能既节省机时又保证差分稳定性,根据柱坐标中FD 算法稳定性准则的经验公式,取
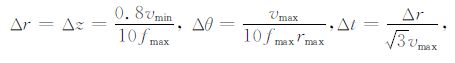
|
式中vmax, vmin 分别表示波在整个计算区域中的最大和最小传播速度,fmax 为声源频谱最大值.
4 差分化时井轴及边界上网格点的处理由于柱坐标系下差分方程在井轴r=0上会出现奇异,因此需对井轴上的场点用守恒积分方法进行处理[8].根据离散规则,处于径向整数网格点的变量有vθ、vz、Tμμ(μ=r,θ,z)以及Tθz,单极源情况vr也需要进行处理.下面给出r=0时(j=0)各变量的处理方法.
为书写方便,定义算符FDFμ 和AVFμ(μ =r,θ,z)分别表示场量在μ 方向的向前之差与向前之和.例如对应力场作用,
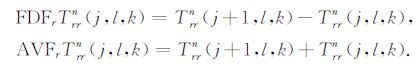
|
定义算符FDBμ 和AVBμ(μ =r,θ,z)分别表示场量在μ 方向的向后之差与向后之和.例如,对速度场作用,
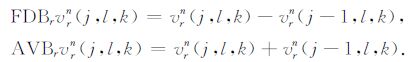
|
利用以上定义的算符,对井轴上场利用守恒积分方法进行如下处理:
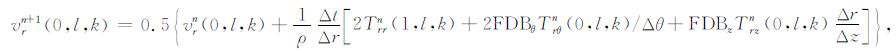
|
(7) |
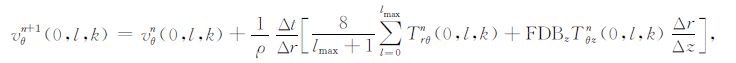
|
(8) |
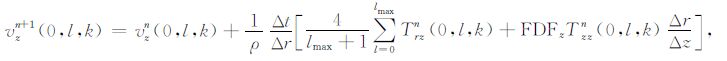
|
(9) |

|
(10) |
其中eμν(μ,ν=r,θ,z)与(4)式中(其他场点)表达式不同,分别为
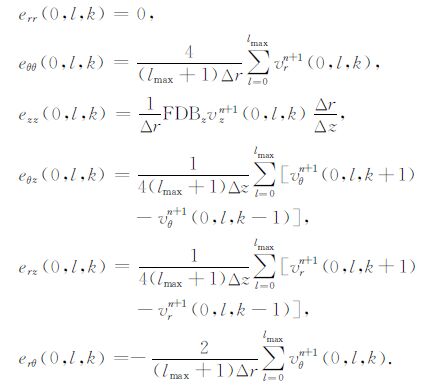
|
对于Tθz,
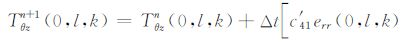
|
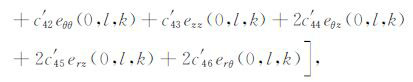
|
(11) |
其中
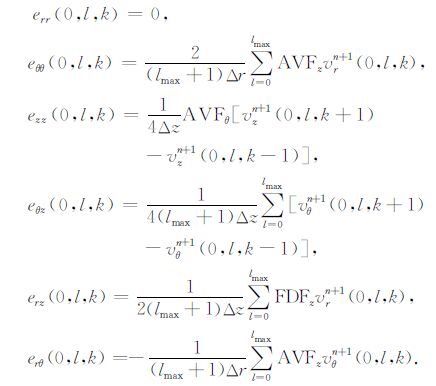
|
为了模拟无限大介质,需要对计算区域的边界,进行处理,消除人为边界造成的反射波.考虑到场点所在网格的交错,可知边界面上需要处理的场点如下:径向边界有Tμμ ,Trz,Trθ,vr,vθ,vz,轴向边界有Tμμ ,Trz,Tθz,vr,vθ,边界角点有Tμμ ,Trz,vr,vθ.处理方法采用Liao等(1984)[13]的吸收边界条件,本文不再详述.
5 方法验证与模拟算例采用SV-FD 方法通过相互垂直的两个偶极子声源数值模拟交叉偶极声波测井的四分量数据.即当偶极子声源沿x方向振动时,x方向和y方向接收到的数据分别标记为xx和xy;当偶极子声源沿y方向振动时,x方向和y方向接收到的数据分别标记为yx和yy.
首先在横向各向同性介质对称主轴与井轴平行的情况下对SV-FD 方法与实轴积分法所得结果进行比较,验证方法的正确性.然后在横向各向同性介质对称主轴与井轴斜交(成任意角度)情况下采用 SV-FD 方法数值模拟了井内正交偶极声源激发的四分量测井数据.
用ε1,ε2,ε3 来描述横向各向同性介质的各向异性程度,则地层5个弹性系数可分别表示为
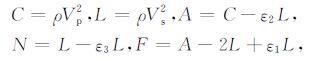
|
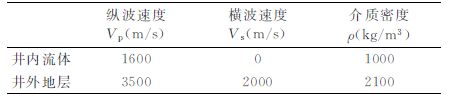
其中ρ,Vp, Vs 分别为密度和纵、横波速度,见表 1.本文数值模拟取ε1 =ε2 =-ε3 =0.3.
|
|
表 1 模型声学参数 Table 1 Acoustic parameters of the model |
在横向各向同性介质对称主轴与井轴平行(VTI)情况下(即将横向各向同性介质对称主轴与井轴的夹角α 设为0°),对三维SV-FD 方法计算的结果和实轴积分法(RAI)所计算的结果进行了对比,结果见图 2,可以看到两种方法得到的波形基本一致.由于有限差分模拟波形存在频散,相位略有差别,但数值模拟结果的精度足以用于分析物理问题.
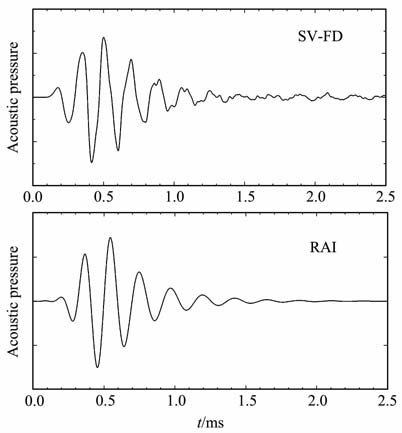
|
图 2 横向各向同性介质对称主轴与井轴平行时有限差分与实轴积分法计算的全波形的比较.接收点距离声源0.2m. Fig. 2 The comparison of full waveforms obtained by SV-FD method and RAI method.The symmetry axis of TI formation is parallel with borehole axis.The source-receiver offset is 0.2 m. |
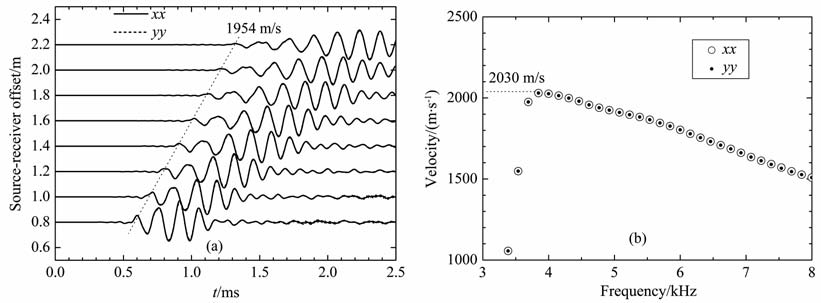
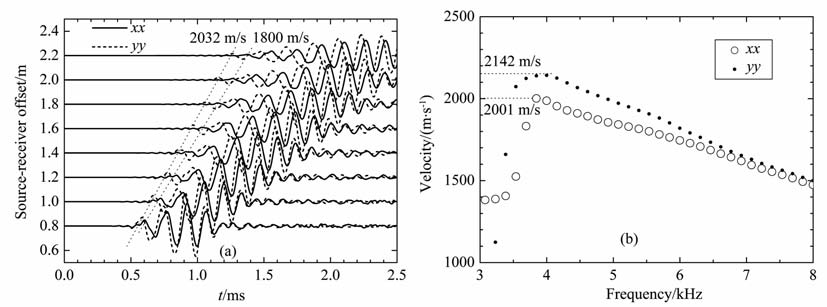
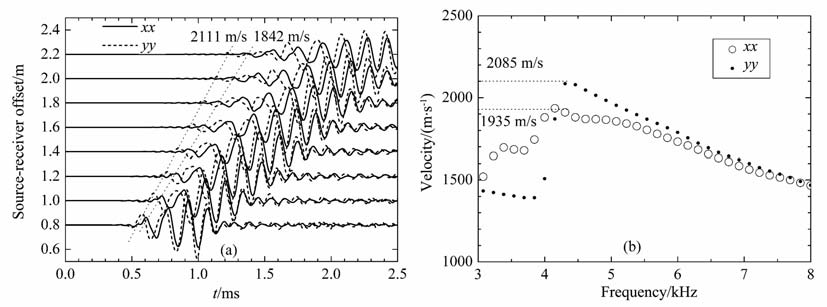
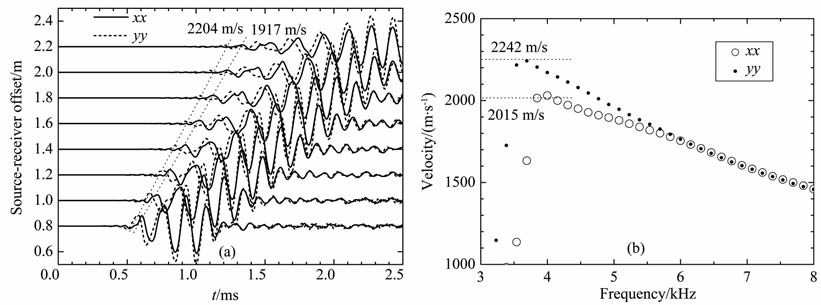
当横向各向同性介质对称主轴与井轴(z轴正向)在oxz平面内成一定角度α 时,接收器水平平面内快、慢横波的极化方向是正交的.以下计算中声源主频为5kHz, 接收器间隔为0.2 m.图 3a~ 图 6a分别为α 等于0°,45°,60°,90°时在硬地层(参数见表 1)中模拟计算的交叉偶极测井xx,yy两分量多道波列.不同接收距波形按第一接收器最大值归一化.图中标出了xx,yy两分量弯曲波第一波至的等相位线,并由各接收器时差计算出了传播速度.由于弯曲波是强频散的导波,由同相轴时差得到的是群速度,并不对应于该方向的地层的横波速度.图 3b~图 6b给出了用频域加权相似法[15]提取的xx,yy两分量弯曲波的频散曲线.
|
图 3 α=0°时xx分量与yy分量弯曲波波形(a)和频散曲线(b) Fig. 3 Flexural waveforms (a) and dispersion curves (b) of xx and yycomponents when α=0° |
|
图 4 α=45°时xx分量与yy分量弯曲波波形(a)和频散曲线(b) Fig. 4 Flexural waveforms (a) and dispersion curves (b) of xx and yy components when α=45° |
|
图 5 α=60°时xx分量与yy分量弯曲波波形(a)和频散曲线(b) Fig. 5 Flexural waveforms (a) and dispersion curves (b) of xx and yy components when α=60° |
当α =0° 时,弯曲波不发生分裂,符合VTI介质的情况,当倾斜角α 逐渐变大时,开始出现快、慢弯曲波的分裂现象.由计算模型图 1 可知,xx/yy分量弯曲波为SV/SH 型偏振,其低频截止频率处对应的速度应为TI地层中准SV 波/纯SH 波速度.通过理论公式[16]可以计算出不同倾斜角度情况下准SV 波和纯SH 波相速度,计算所得结果列于表 2中.从图 3b~ 图 6b可见,对不同的倾斜角xx和yy分量的频散曲线低频截止频率处的相速度与表 2中理论公式计算结果基本符合,进一步验证了模拟结果的正确性.倾斜角不为零时,xx和yy分量的频散曲线低频段分裂,在高频段重合,因此当正交偶极源频带的最低频率较高时,将观察不到TI地层弯曲波分裂现象.偶极源的频带为4~6kHz时弯曲波分裂现象最明显.这一现象和声源的频谱有关,本文采用主频为5kHz的瑞克子波,其能量主要集中在4~6.5kHz的频段内.
|
|
表 2 由理论公式计算的不同倾斜角度情况下准SV波和纯SH波相速度 Table 2 Phase velocities of qausi-SV wave and SH wave calculated by theoretical formula with different dip angles |
|
图 6 α=90°时xx分量与yy分量弯曲波波形(a)和频散曲线(b) Fig. 6 Flexural waveforms (a) and dispersion curves (b) of xx and yy componentswhen α = 90° |
针对横向各向同性(TI)介质对称主轴与井轴斜交这一复杂井孔声场问题,本文采用柱坐标系交错网格三维应力-速度有限差分方法,数值模拟了TI介质对称主轴与井轴成不同角度情况下,正交偶极子激发声场的弯曲波分裂现象.由于含有圆柱型井孔,采用柱坐标系方便有限差分的网格划分,对于柱坐标系下井轴上的奇异点,用守恒积分方法进行了处理.数值模拟结果显示,当夹角逐渐变大时,开始出现快、慢弯曲波的分裂现象,xx和yy分量弯曲波的频散曲线在低频段分裂,低频截止频率处速度能够与理论公式计算所得地层准SV 波和纯SH波相速度符合,而随着频率增高,频散曲线逐渐重合.有限差分方法可以模拟TI地层中大斜度(任意角度)井的全波瞬态声场,为大斜度井声测井分析和各向异性反演提供理论基础.
| [1] | Ellefsen K J, Cheng C H, Toksoz M N. Applications of perturbation theory to acoustic logging. J. Geophys. Res. , 1991, 96(B1): 537-549. DOI:10.1029/90JB02013 |
| [2] | Sinha B K, Norris A N, Chang S K. Borehole flexural modes in anisotropic formations. Geophysics , 1996, 59(7): 21-33. |
| [3] | Zhang B X, Wang K X. Theoretical study of perturbation method for acoustic multipole logging in anisotropic formation. J. Acoust. Soc. Am. , 1996, 99(5): 2674-2685. DOI:10.1121/1.414855 |
| [4] | Mittet R, Renlie L. High-order, finite-difference modeling of multipole logging in formations with anisotropic attenuation and elasticity. Geophysics , 1996, 61(1): 21-33. DOI:10.1190/1.1443942 |
| [5] | Liu Q H, Sinha B K. Multipole acoustic waveforms in fluid-filled boreholes in biaxially stressed formations: A finite-difference method. Geophysics , 2000, 65(1): 190-201. DOI:10.1190/1.1444710 |
| [6] | 马 俊, 王克协, 李 刚等. 应力诱导各向异性介质包围井孔中声场的三维SV-FD数值模拟. 中国地球物理学会第十九届年会, 2003. 546. Ma J, Wang K X, Li G, et al. 3D SV-FD numerical simulation of borehole embedded in stress-induced anisotropic formation (in Chinese). 19th Ann. Mtg., Chin. Geophys. Soc., 2003. 546 |
| [7] | 马 俊, 王克协, 李 刚等. 套管井应力诱导各向异性井孔声场的三维SV-FD数值模拟. 中国地球物理学会第二十届年会, 2004. 504. Ma J, Wang K X, Li G, et al. 3D SV-FD numerical simulation of cased hole embedded in stress-induced anisotropic formation (in Chinese). 20th Ann. Mtg., Chin. Geophys. Soc., 2004. 504 |
| [8] | 马 俊, 王克协, 李 刚等. 各向异性介质包围井孔中声场的三维SV-FD数值模拟方法. 中国地球物理学会第十八届年会, 2002. 415. Ma J, Wang K X, Li G, et al. 3D SV-FD numerical simulation method of borehole embedded in anisotropic formation (in Chinese). 18th Ann. Mtg., Chin. Geophys. Soc., 2002. 415 |
| [9] | Wang X M, Hornby B, Dodds K. Dipole sonic response in deviated boreholes penetrating an anisotropic formation. 72nd Ann. Internat Mtg., Soc. Expi. Geophys.. Expanded Abstracts, 2002. 360 |
| [10] | Sinha B K, Simsek E, Liu Q H. Elastic-wave propagation in deviated wells in anisotropic formations. Geophysics , 2006, 71(6): 191-202. DOI:10.1190/1.2358402 |
| [11] | 闫守国, 马 俊, 谢馥励等. 非轴对称TI 介质包围井孔声场的三维SV-FD数值模拟. 中国地球物理学会第二十三届年会, 2007. 449. Yan S G, Ma J, Xie F L, et al. 3D SV-FD numerical simulation of borehole embedded in nonaxisymmetric transversely isotropic formation (in Chinese). 23rd Ann. Mtg., Chin. Geophys. Soc.,2007. 449 |
| [12] | 何 晓, 胡恒山. 各向异性地层井孔偶极声场的三维有限差分数值模拟. 中国地球物理学会第二十五届年会, 2009. 234. He X, Hu H S. 3D finite difference numerical simulation of dipole acoustic field in borehole embedded in anisotropic formation (in Chinese). 25rd Ann. Mtg., Chin. Geophys. Soc., 2009. 234 |
| [13] | Liao Z P, Wong H L, Yang B P, et al. A transmitting boundary for transient wave analyses. Scientia Sinica (Series A) , 1984, 27(10): 1063-1076. |
| [14] | Taflove A. Computational Electromagnetics: The Finite-Difference Time-Domain Method. Boston: Artech House, 1995. 36~38 |
| [15] | Nolte B, Rao V N R, Huang X. Dispersion analysis of split flexural waves. Borehole Acoustics and Logging/Reservoir Delineation Consortia Annual Report, MIT. 1997 |
| [16] | White J E. Underground Sound: Application of Seismic Waves. New York: Elsevier Science Ltd., 1983 : 38 -41. |
 2011, Vol. 54
2011, Vol. 54