直升机时间域航空电磁法(Helicopter-borne time-domainel ectromagnetic method, HTEM)的系统校准可消除外界环境对仪器的时变影响,是仪器研发及工程应用中衡量系统性能的关键问题之一[1~4].传统的校准方法是利用飞行测试已知矿区的方式来校准仪器系统,而探测目标区域地质情况的非线性,使得仪器校准和仪器间性能难于对比分析,同时矿区少有平坦的勘察区域,常因吊舱装置频繁的运输和高额的花费而放弃实验[5].殷长春等[5]研究了航空电磁法对导体覆盖层上的环线异常检测方法,Macnae James和Davis Aaron分别从航空电磁系统对地面环线的监测[6]、频率域地面环线的校准[7]、时间域地面环线的波形测量[8, 9]、基于地面环线的时间域航空电磁法系统的校准[10]和基于地面环线方式量化航空电磁法的系统特征[11]等方面做了研究.地面环线检测方法适用于仪器研发初期系统性能参数的评定和研发后期不同航空电磁仪器系统性能的对比,但其有两方面不足:一是校准信号通常受大地覆盖层阻抗特性的影响导致不同地点校准信息难于对比,校准方法不便于解决呈低阻区域的系统校准问题[5];二是固定地面100 m×100 m 方形环线的校准装置无法实现HTEM400~500m 飞行运动过程中的仪器校准.为了弥补不足,采用多匝小线圈的吊舱校准装置.目前,HTEM 固定支架的吊舱装置采用补偿环的方式实现电流供电期间抵消接收处的一次感生场,进而提高大地二次感生场信号的动态范围.最早提出该想法的Aeroquest公司分析其三角发射波形的ON-TIME 数据可获知大地高导覆盖层信息[12, 13],其IV 型仪器采用了偏心补偿环式吊舱校准装置实现了空中飞行过程中仪器的校准[14].由于VTEM 大磁矩的多边形波发射,有利于深层矿体的探测[15~17].这里,我们的HTEM 系统结合两者的优势,吊舱采用发射装置、接收装置和补偿环同心的硬支架结构,采用多边形电流的激励方式.本文研究的校准装置构建在同心补偿式的HTEM系统上,解决了空中飞行过程中系统难校准的问题.
吊舱校准装置的电磁模型是以自由空间环线模型为基础的,考虑两类电磁传播途径:一类是从发射线圈直接耦合到接收线圈处的路径(Transmitter to Receiver, TR),另一类是经校准线圈后耦合到接收线圈处的路径(Transmitter to Loopto Receiver, TLR).参考殷长春等[5]关于地面环线异常模型中发射线圈、异常线圈、大地和接收线圈四者之间电磁传播路径的分析,同时考虑吊舱校准线圈直径小,激发大地强度弱的特点,假设从发射线圈由经大地传递到接收线圈的路径(Transmitter to Earth to Receiver, TER)和校准线圈经大地传递到接收线圈的路径(Loop to Earth to Receiver, LER)可忽略.计算环线模型有两种常规方法:一是采用傅里叶变换,把发射电流和系统响应转换到频率域后乘积,之后由傅里叶逆变换得到时间域响应[18];二是采用发射电流或其时间导数卷积系统方波响应的方法[19, 20].本文借鉴第二种方法,从描述线性电流源与磁场关系的毕奥-萨伐尔定律出发,通过分离时间和空间参量的方式,对与时间参量关联的电流导数和系统响应做卷积处理,对与空间参量关联的线圈间互感做乘积处理.从模型的数值分析中,本文获得同心补偿HTEM 横向和纵向的磁场分布,从磁场和磁通两方面明确补偿环与接收线圈半径的关系,再通过分析线圈装置间互感的影响确定校准装置的半径及位置,最后分析校准线圈的时间常数得到校准信号e指数衰减特征,接收线圈的阻尼特性直接影响信号检测起点的选择,而该阻尼特性可通过调整线圈的匹配电阻得以改善.
校准装置安装在北京航空物探遥感中心和吉林大学联合研发的HTEM 吊舱系统上[21, 22].通过长春地质宫TEM 地面装置实验说明校准信号e指数衰减特点,验证了校准装置LR 模型的合理性.通过长春大鹅岛HTEM 装置上校准线圈位置的移动实验,说明了校准装置引起的互感影响.
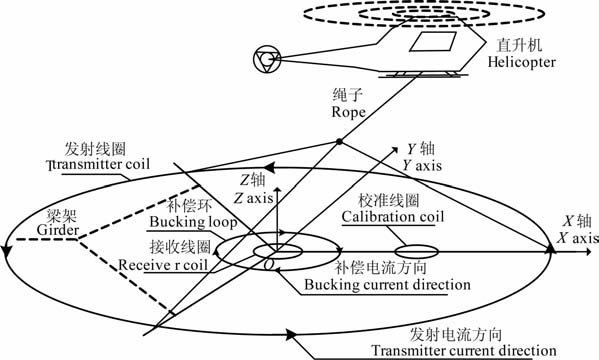
2 同心补偿HTEM 吊舱装置的模型建立HTEM 的吊舱装置是直升机舱外系统的主体,负责TEM 信号的发射和接收,其结构见图 1.吊舱包括四个部分:一是包含单匝反向电流的同心补偿环和5匝直径15m 发射线圈的发射装置;二是中心处获取TEM 信号的接收装置;三是本文研究的吊舱校准装置;四是保持发射、接收和补偿环处于水平同心的梁架和负责托起吊舱绳子的悬挂装置.当直升机在空中水平匀速飞行时,吊舱笛卡尔坐标系的原点是接收线圈的圆心,X轴为飞行方向,吊舱XOY平面平行于地面.当发射电流方向如图 1所示时,根据右手定则,Z轴向上为正方向.吊舱校准装置在直升机水平匀速空中飞行过程中工作,吊舱装置之间位置固定,则校准装置的研究可从吊舱装置的空间模型和与时间有关的线圈电路参数模型两方面描述.
|
图 1 HTEM 吊舱装置示意 Fig. 1 The schematic diagram of the HTEM bird device |
发射装置产生的总电磁能量一部分直接耦合到接收装置中使其获得TR 响应,一部分经由闭合校准线圈再传递到接收装置中的TLR 响应.研究TR和TLR 的方法是基于描述线元与磁场关系的毕奥-萨伐尔定律和描述环线内交变磁通产生感生电动势的法拉第电磁感生定律.先分析TR 响应中的磁场,见式(1).
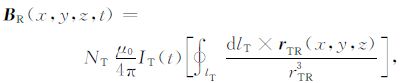
|
(1) |
其中,BR(x,y,z,t)为TR 响应在接收处的磁场,NT 为发射线圈匝数,IT(t)为发射线圈内电流,rTR(x,y,z)为发射环上线元到接收处的矢径,其距离为rTR,μ0 为真空中磁导率.式(1)描述的交变磁场在接收线圈中产生感生电动势εTR(t):
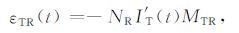
|
(2) |
其中,NR 为接收环的匝数,I′T(t)为发射电流的时间导数,发射环对单匝接收环的互感MTR 为
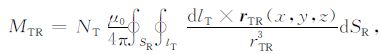
|
(3) |
其中,SR 为接收线圈围成的曲面.同理,TLR 响应中校准线圈内的感生电动势εTL(t)为
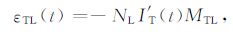
|
(4) |
其中,NL 为校准线圈的匝数,发射环对校准线圈的互感MTL 为
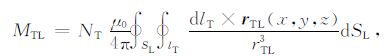
|
(5) |
其中,SL 为校准线圈围成的曲面.校准线圈在接收处的感生电动势εLR(t)为
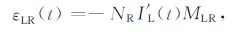
|
(6) |
其中I′L(t)为校准线圈内感生电流导数,校准线圈对接收环的互感为
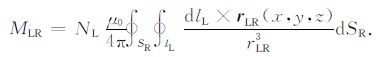
|
(7) |
则接收线圈获得总的感生电动势为
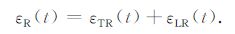
|
(8) |
设接收线圈和校准线圈的系统零状态响应分别为HR(t)和HL(t),则接收线圈两端输出电压uR(t)为
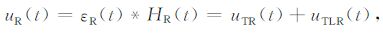
|
(9) |
其中TR 影响的输出电压uTR(t)为
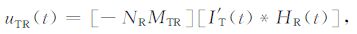
|
(10) |
TLR 影响的输出电压uTLR(t)为
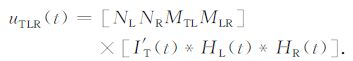
|
(11) |
由式(10)和式(11)知,接收线圈的输出电压包括两类参数,一类是与形状及位置有关的空间常数,TR响应中的-NRMTR 和TLR响应中的NLNRMTLMLR,另一类是与线圈电路模型有关的时间参数,TR 响应中的I′T(t)*HR(t)和TLR 响应中的I′T(t)*HL(t)*HR(t).空间常数可由装置之间的互感给出,时间参数通过发射电流的波形、校准线圈和接收线圈的电路模型给出.
2.2 线圈电路的时间参数模型线圈参数模型的研究从发射电流曲线形态入手.本文采用的发射电流为25 Hz的双极性多边形波,其半波描述见图 2.其中,电流上升时间tup1 取3.5ms, 平顶时间tup2 取4 ms, 关断时间tdown 取1.2ms, 电流第一次上升值Iup1取280A,第二次上升值Iup2取300A,则发射电流导数函数表达为:
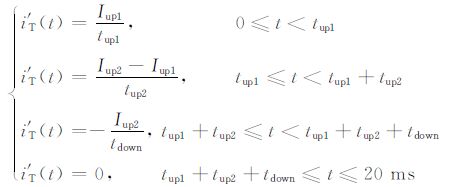
|
(12) |

|
图 2 发射电流波形示意 Fig. 2 The schematic diagram of the transmitter current waveform |
在TLR 响应中,校准线圈为RL 串联模型电路,其零状态响应HL(t),见式(13):
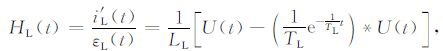
|
(13) |
其中校准线圈的时间常数TL =LL/RL,LL 为校准线圈中电感,RL 为校准线圈电阻,U(t)为阶跃函数,i′L(t)为校准线圈内电流导数,εL(t)为校准线圈的感生电动势.
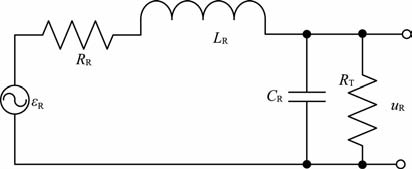
在TLR 和TR 响应中,接收线圈为电感、电容、内阻和匹配电阻构成的二阶模型,见图 3.
|
图 3 接收线圈等效电路 εR 为接收线圈感生电动势,uR 为接收线圈的输出电压,RR 为接收线圈内阻,LR 为接收线圈电感,CR 为接收线圈电容,RT 为并联到线圈两端的匹配电阻. Fig. 3 The receiving coil equivalent circuit |
接收线圈系统的零状态响应HR(t)为
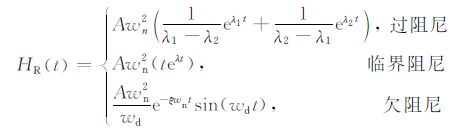
|
(14) |
其中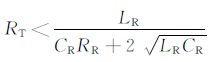
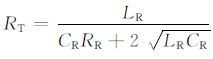
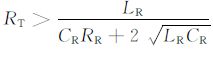
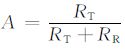
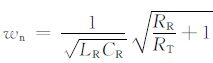
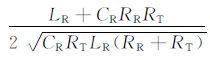
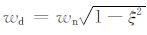
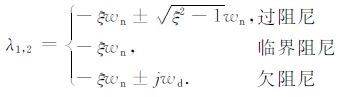
|
本文对校准线圈的检测是在电流关断为零的 OFFTIME 阶段,采用获取校准线圈e指数衰减的时间常数TL 的特征,来校准仪器系统.而校准信号起始点的选取与接收线圈HR(t)的阻尼特性直接相关,通过模型的数值分析研究校准装置的空间和时间特性.
3 模型的数值分析吊舱校准装置的研究包括线圈的空间信息和信号检测方法两方面,其中校准线圈的大小及位置与发射线圈、补偿环和接收线圈大小紧密相关,先确定补偿环的大小,而后确定校准线圈的大小及装置的位置.校准线圈的电感和电容参数直接影响校准信号衰减时间的长度及初始信号的幅值,而接收线圈的阻尼特性则直接影响校准信号检测的时间起点.这里,HTEM 发射装置为5 匝半径7.5 m 的线圈,接收装置为110匝半径0.55m 的线圈.
3.1 发射装置同心补偿方式的空间磁场分布采用硬支架结构的HTEM 吊舱系统的目的之一是通过调整补偿环来提高大地二次场信号的动态范围.
通过式(1)获得纵向自由空间XOZ平面的磁场空间分布,无补偿环磁场分布见图 4a,有半径1.64m的补偿环见图 4b.图 4坐标系的建立与图 1相同,X轴表征场点的横向位置,Z轴表征场点的纵向位置.根据磁场空间分布的指数规律,这里对空间任意点的总磁场取自然对数来表征磁场强度,图例中红色表征磁场强度大,蓝色表征磁场强度小.图 4a中,磁场最强处位于X轴7.5 m 且Z轴为0 m处,说明发射环线上的磁场最强.由磁场等值线的曲线形态和表征磁场强度方向的箭头,说明在Z轴-10~0m 以内,空间磁场分布的近区域效应强,小于-10m 以外,磁场区域效应减弱,呈椭球状扩散效应.含补偿环的图 4b与图 4a对比,在Z轴-5~0m以内,补偿环明显影响磁场的近区效应,减弱中心处的磁场强度,而小于-10m 以外的磁场分布仍然呈现椭球状扩散,可近似为无补偿环状态.常规 HTEM 的飞行调查高度为30 m, 则发射装置中补偿环的影响可忽略.

|
图 4 XOZ平面上无补偿线圈(a)及半径1.64m 补偿线圈(b)的发射装置磁场自然对数分布 Fig. 4 Natural logarithm of magnetic field distribution on XOZ plane without bucking loop (a) and with bucking loop radius 1.64 m (b) |
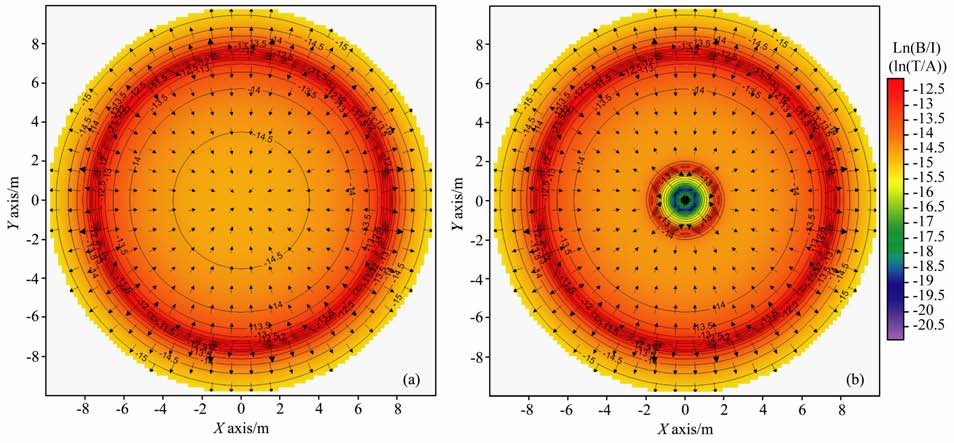
校准装置固定在吊舱装置上,处于发射的近区磁场中,通过分析吊舱装置XOY平面上空间磁场分布情况,初步确定吊舱校准装置的大致区域.无补偿环的磁场分布图 5a,同样说明磁场最强处位于发射线圈上,磁场强度等值线呈同心圆方式向圆心处扩散.含半径1.64m 补偿环的图 5b与图 5a对比,补偿环让接收处的磁场减弱,则接收处的TR 响应被减弱.为了保证校准装置在有无补偿状态下受到同样的磁场激励,则校准装置应摆放在补偿环与发射线圈之间的水平位置上.
|
图 5 XOY平面上无补偿线圈(a)及含半径1.64m 补偿线圈(b)的发射装置磁场自然对数分布 Fig. 5 Natural logarithm of magnetic field distribution on XOY plane without bucking loop(a) and with bucking loop radius 1.64 m (b) |
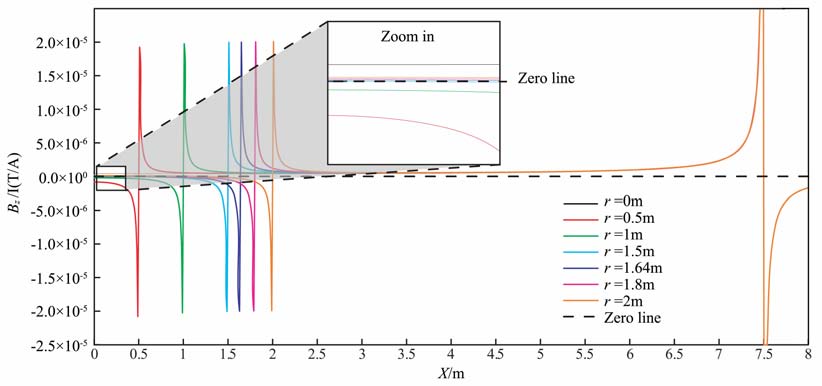
在校准装置位置确定之前需要确定补偿环的精确位置.图 6说明不同补偿环半径下Z=0处径向Z方向磁场Bz的分布.补偿环的引入导致接收线圈处 TR 引起的磁场被削弱,当半径小于1.5m 时,从图 6中放大区域看出中心点处磁场为负值,与无补偿环时磁场反向,此状态为过补偿.补偿环半径继续变大,接收处的磁场中心部分逐步变为正值.若TR 响应中感生电动势由正趋近零时,此状态为最佳补偿,若电动势TR正值过大则欠补偿,失去补偿环的作用.
|
图 6 Z=0时,补偿环不同半径下径向磁场Z方向的分布 Fig. 6 The radial Z direction magnetic field distribution of bucking loop with different radius when axis |
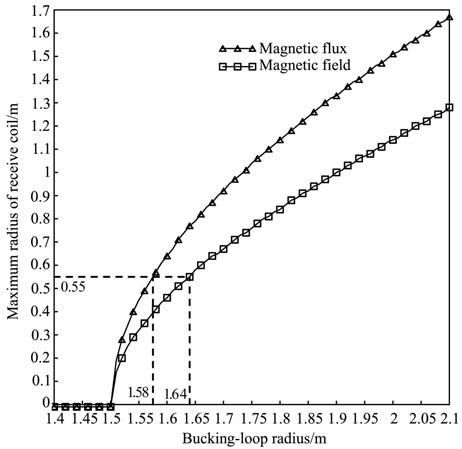
图 7描述了补偿环半径与接收线圈半径最大值的关系.磁场曲线表明接收线圈所围成的面积内磁场都是正向激励,而磁通曲线表明接收线圈所围成面积内磁场存在正向和负向激励,但要求正向激励要强于负向激励,其差值趋向于零.在考虑实际补偿环需调整的情况,当接收线圈半径为0.55m 时,补偿环的半径范围是1.58~1.64m.通过式(11)的计算,当无补偿TR 响应为10.9V 时,相同条件下,半径为1.58m 和1.64m 补偿环的TR 响应幅度分别为0.0646V 和0.5V.虽然相对无补偿环时,发射装置的有效面积减少了0.89%~0.96%,但有效信号的动态范围却可提高26.7~44.5dB.
|
图 7 接收线圈半径最大值与补偿环半径的关系 Fig. 7 Relationship between receive coil's maximum radius and bucking loop radius |
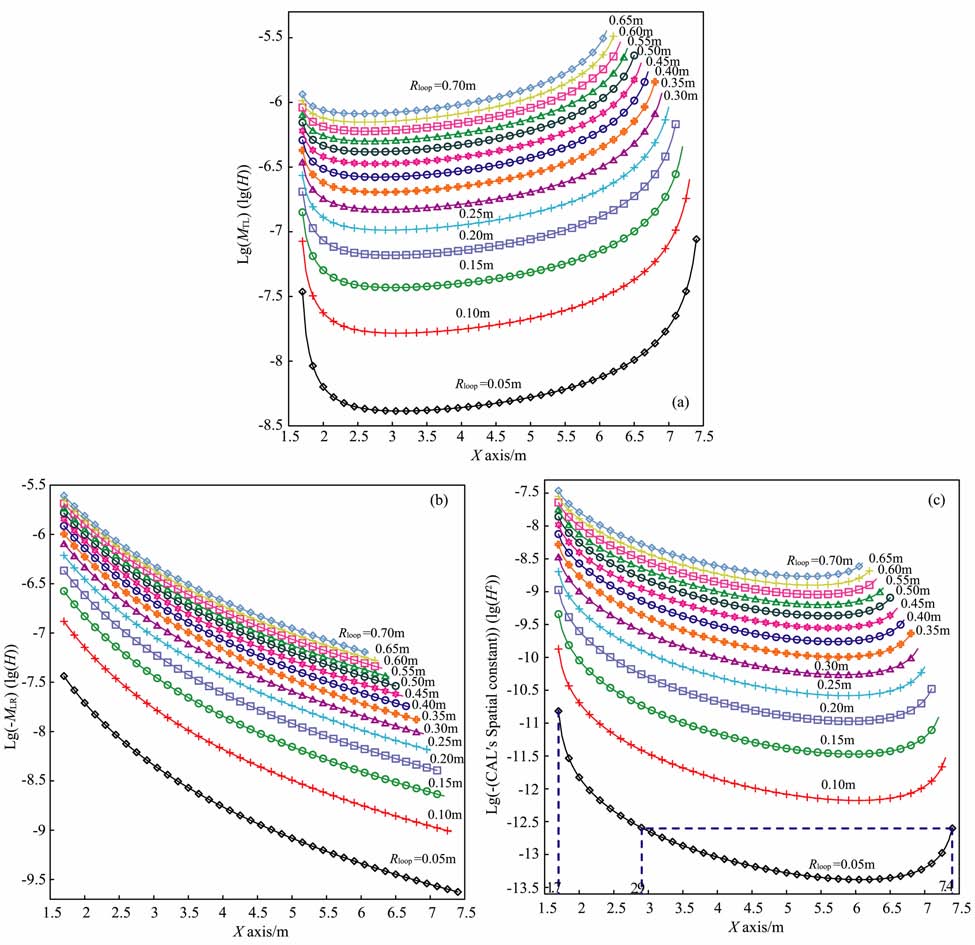
由式(11)可知,TLR响应的空间常数NLNRMTLMLR影响uTLR(t)信号的强度,在接收线圈和校准线圈匝数不变时,互感MTL 和MLR 直接影响校准信号的强度.为容易检测强度大的校准信号,需要空间常数越大越好.当补偿环半径固定为1.64m 时,沿X轴向移动不同半径的校准线圈可以得到MTL、MLR 和校准装置影响的空间常数,分别为图 8(a, b, c).从图 5b和图 7可初步确定吊舱校准装置中心位置应该在1.5~7.5 m 之间,所以图 8的X轴限定在此范围内.为更好展现互感值的差异,图 8的数值分别取以10为底的对数处理,值得注意的是:MTL 为正值,MLR 为负值.图 8中Rloop 为校准线圈的半径,在X轴向位置相同条件下,Rloop 值越大,响应越大.当固定Rloop 后,随着校准装置圆心X坐标从中心向发射线圈靠近时,MLR 一直变小,而MTL 和校准线圈空间常数先变小而后增大,该效应是补偿环影响的结果.当Rloop 确定后,校准装置的空间位置由空间常数确定.例如,在图 8c中,采用半径0.05 m 的校准线圈,其中心X坐标在1.7~2.9m 时,曲线具有单调性,选择1.7 m 为最佳;当校准线圈因吊舱结构的配重问题不能安置在1.7~2.9 m 的区域时,考虑2.9~7.4 m 区间内,同一强度可由两个位置对应,与6~7.4m 区间相比,2.9~6m 区间的强度变化要缓,工程实现较容易.
|
图 8 补偿环半径1.64m 时,发射线圈对不同半径及位置下校准线圈的互感影响(a),不同半径及位置的校准线圈对接收线圈的互感影响(b),不同半径及位置校准线圈的空间常数影响(c) Fig. 8 Mutual inductance between transmitter and CAL coil (a) ,negative mutual inductance between CAL and receive coil(b) ,and negative spatial constant of CAL coil(c) when bucking loop radius =1.64 m |
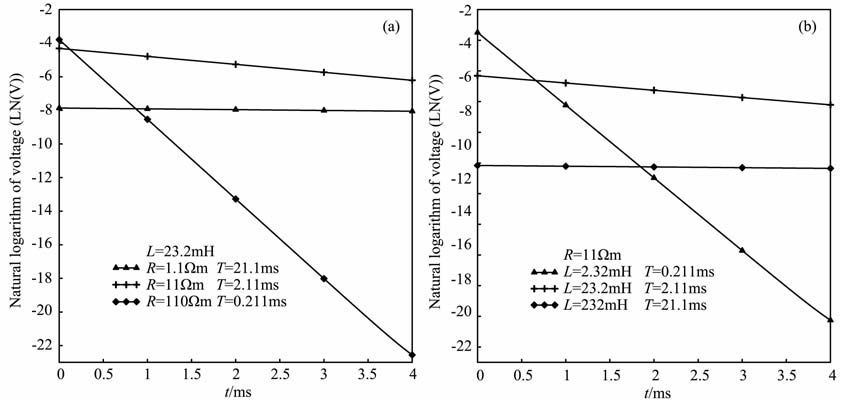
由式(11)、(12)、(13)和(14)得到,校准信号衰减时间长短取决于校准线圈的时间常数和初始信号幅值.以校准线圈圆心X位置2.2m 处、电阻11Ωm、电感23.2mH、匝数100匝及半径为0.8m 为基本值,分别改变电阻和电感,校准线圈OFFTIME 的响应曲线,见图 9.由式(13)知,曲线呈现e指数衰减,所以对校准信号取自然对数处理.从图 9a得到,当电感不变时,电阻越小,校准线圈的时间常数越大,信号衰减越慢.从图 9b得到,当电阻不变时,电感越大、校准线圈的时间常数越大,信号衰减越慢.在保证大幅度值的初始信号条件,时间常数向小微调时,可采用减少电感的方法,而时间常数向大微调时,可采用减少电阻的方法.
|
图 9 当电感为23.2mH 时(a)及电阻为11Ωm (b)时,改变电阻得到的校准线圈响应 Fig. 9 The calibration coil, s response of varying R when L = 23.2 mH(a)and R=11Ωm (b) |
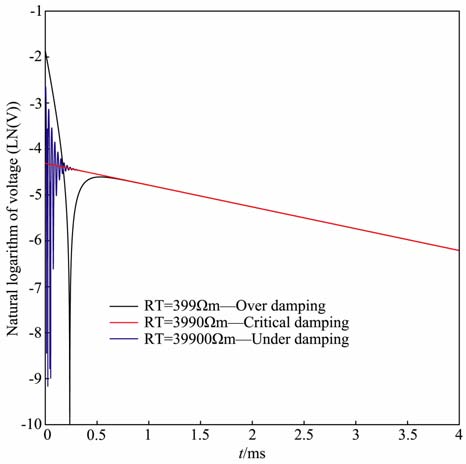
在关断电流后期,校准信号的检测时间起点取决于接收线圈的阻尼特性.由式(14)出发,以电阻18.5Ωm、电感37.4mH、电容586pF、匝数110匝、直径1.1m 作为接收线圈的基本值.通过改变线圈匹配电阻RT的大小进而改变接收线圈的阻尼状态,见图 10.当接收线圈处于临界阻尼时,时间起点可选择从OFFTIME关断后的0ms开始.当接收处于欠阻尼状态时,在OFFTIME 早期信号有震荡,检测信号起点需避让震荡过程.当接收线圈处于过阻尼状态时,在OFFTIME 早期信号不满足e指数衰减规律.图 10中可以看出,如果从1ms后检测校准信号可避开校准信号早期受接收线圈阻尼特性的影响,获得稳定的e指数衰减信号.
|
图 10 不同接收匹配电阻RT 时校准线圈的响应 Fig. 10 The calibration coil's response of varying receive coil RT |
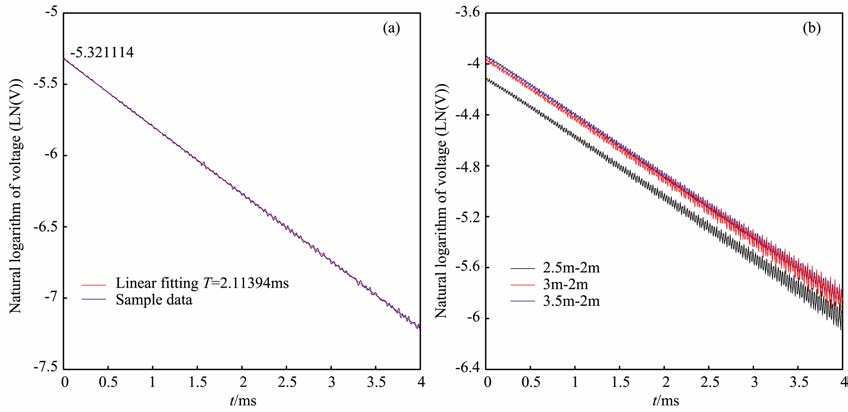
为了说明本文提出模型及方法的正确性,我们制作了匝数100、直径0.8 m、电阻11 Ωm、电感23.2mH、计算时间常数为2.11 ms的环形校准线圈.为说明校准线圈的信号衰减特点,2010 年8 月20日在长春地质宫前广场上,采用地面40m×40m中心装置的TEM 测量,校准线圈同心放置于接收线圈上方,做1024 次叠加后的校准线圈响应(见图 11a).采集的数据取自然对数后进行线性拟合获得校准线圈的时间常数T为2.11394ms, 相对计算时间常数的误差为0.23%.该实验说明校准装置LR 模型是正确的.
|
图 11 地面TEM 检测校准线圈的响应(a)及HTEM 吊舱校准装置的线圈响应(b) Fig. 11 The calibration coils response of ground TEM experiment (a) and the coll response of HTEM calibration device (b) |
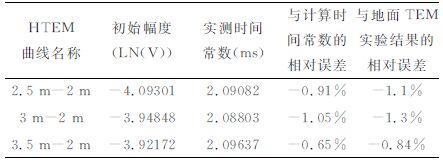
为说明校准装置空间位置变化导致校准信号的差异,2010年9 月9 日在长春大鹅岛的HTEM 装置上,校准线圈中心分别放置在X轴2m、2.5m、3m和3.5m 处检测.由式(11)和式(13)知,位置移动会改变信号响应强度,但不改变信号曲线衰减形态,即时间常数不变,则数据做6 次叠加处理后分别采用2.5m-2m、3m-2m, 3.5m-2m 的曲线消除非校准线圈影响,见图 11b.同样线性拟合处理后,获得校准线圈时间常数及相对2 m 时曲线初始值的检测效果,见表 1.由图 11b和表 1 得,校准线圈中心距X轴2m时的信号强度最大,随着远离中心,与2m的偏差变大,信号强度减弱,且强度随位移的变化量变小,这与图 8c中半径0.4m 的曲线在2m-3.5m区间内呈现的形态相吻合.校准线圈的时间常数检测误差最大1.3%,说明实测结果与理论计算吻合.
|
|
表 1 HTEM吊舱校准装置响应测试结果 Table 1 The test result of HTEM calibration device response |
本文将同心补偿式HTEM 吊舱校准装置的模型分解为与空间参数有关的吊舱装置空间模型和与时间参数有关的线圈电路参数模型,通过吊舱装置的模型分析可得如下结论:
(1) HTEM 吊舱的同心补偿环是以损失等效发射面积来提高有效大地二次场感应场信号的一种直接方法.这里,HTEM 采用5 匝半径7.5 m 的发射线圈,半径0.55 m 的接收线圈,当补偿环半径为1.58m时,发射面积损失0.89%,但信号动态范围可提高44.5dB.当飞行高度30 m 时,补偿环效应可以忽略.
(2) HTEM 同心补偿的吊舱校准装置水平放置在补偿环与发射线圈之间.校准线圈匝数越多,半径越大,越靠近补偿环,则校准线圈空间常数越大、校准响应越强.
(3) 校准装置的信号呈e指数衰减.校准线圈电感越大、电阻越小,其时间常数越大,信号衰减越慢.OFFTIME 的早期校准信号受接收线圈的阻尼特性影响,信号检测应以稳定e指数衰减时为起点,而线圈的阻尼特性可通过调整匹配电阻得以改善.
最后,校准信号检测实验和校准线圈位置移动实验反映了校准线圈特性时间常数的相对检测误差小于1.3%,说明了校准装置电感电阻串联模型的合理性、校准装置间互感的影响及检测方法的正确性.对于接收线圈和补偿环与发射线圈偏心的吊舱系统,同样可以采用本文提出的研究方法,只需改变接收线圈的中心位置做相应研究.同理,高阻地层上的环线静态检测只需把校准线圈水平放置到地面上,改变本文的校准线圈位置即可.本文的吊舱装置可校准HTEM 接收线圈的Z分量,在此基础上,进一步研究非水平共面装置可解决接收线圈X、Y分量的校准问题.
致谢感谢吉林大学地球信息探测仪器教育部重点实验室提供了研究平台,感谢吉林大学时间域航空电磁组于生宝、周逢道、嵇艳鞠、朱凯光、张爽、刘焕江和任广群老师分别在TEM 发射系统、接收线圈、校正环线计算、数据处理、装置系统安装等方面给予的指导,感谢北京航空物探遥感中心陈斌、罗鸥、曹学峰和李永兴先生在直升机及仪器需求上给予的帮助.
| [1] | Fountain D. Airborne electromagnetic systems-50years of development. Exploration Geophysics , 1998, 29(2): 1-11. DOI:10.1071/EG998001 |
| [2] | 张昌达. 航空时间域电磁法测量系统: 回顾与前瞻. 工程地球物理学报 , 2006, 3(4): 265–273. Zhang C D. Airborne time domain electromagnetic system: look back and ahead. Chinese Journal of Engineering Geophysics (in Chinese) , 2006, 3(4): 265-273. |
| [3] | Fountain D. 60 years of airborne EM-focus on the last decade. AEM2008-5th International Conference on Airborne Electromagnetic, Haikko Manor, Finland, 2008 |
| [4] | Sattel D. An overview of helicopter time-domain EM systems. Preview , 2009, 138: 59. |
| [5] | Yin C C, Hodges G. Wire-loop surface conductor for airborne EM system testing. Geophysics , 2009, 74(1): F1-F8. DOI:10.1190/1.3008055 |
| [6] | Macnae J, Davis A. Surface loop monitoring of airborne electromagnetic systems. SEG Int'l Exposition and 74th Annual Meeting, Denver, Colorado, 2004 |
| [7] | Davis A C, Macnae J C. Ground loop calibrations for frequency domain airborne EM surveys. Abstracts-Geological Society of Australia, 2006. 82 |
| [8] | Davis A C, Macnae J. Measuring the waveform of time domain AEM systems using a ground loop. Canning Bridge, West. Aust.: Promaco Conventions, 2007 . |
| [9] | Davis A, Macnae J. Measuring AEM waveforms with a ground loop. Geophysics , 2008, 73(6): F213-F222. DOI:10.1190/1.2976791 |
| [10] | Davis A C, Macnae J. Calibration of time domain AEM systems using a ground loop. Canning Bridge, West. Aust.: Promaco Conventions, 2007 . |
| [11] | Davis A C, Macnae J. Quantifying AEM system characteristics using a ground loop. Geophysics , 2008, 73(4): F179-F188. DOI:10.1190/1.2943189 |
| [12] | Svilans M. Quantitative Interpretation of Responses of Helicopter-borne Concentric Loop EM Geophysical Survey Systems. Ottawa, Ontario: Carleton University Earth Sciences, 2006 . |
| [13] | Balch S J, Boyko W P, Paterson N R. The AeroTEM airborne electromagnetic system. The Leading Edge , 2003, 22(6): 562-566. DOI:10.1190/1.1587679 |
| [14] | 滕吉文. 强化第二深度空间金属矿产资源探查, 加速发展地球物理勘探新技术与仪器设备的研制及产业化. 地球物理学进展 , 2010, 25(3): 729–748. Teng J W. Strengthening exploration of metallic minerals in the second depth space of the crust, accelerating development and industralization of new geophysical technology and instrumental equipment. Progress in Geophys. (in Chinese) , 2010, 25(3): 729-748. |
| [15] | Walker S E, Rudd J. Extracting more information from on-time data. ASEG20th International Geophysical Conference and Exhibition, Adelaide of Australia, 2009. 64 |
| [16] | Witherly K, Irvine R. The VTEM heli-time domain EM system-four case studies. ASEG18th International Geophysical Conference and Exhibition, Melbourne of Australia, 2006 |
| [17] | Cunion E. Comparison of ground TEM and VTEM responses over kimberlites in the Kalahari of Botswana. ASEG20th International Geophysical Conference and Exhibition, Adelaide of Australia, 2009. 22~25 |
| [18] | Huang H P. Locating good conductors by using the B-field integrated from partial dB/dt waveforms of time domain EM systems. SEG/San Antonio 2007 Annual Meeting, 2007. 688~692 |
| [19] | Liu G M. Effect of transmitter current waveform on airborne TEM response. Exploration Geophysics , 1998, 29(2): 35-41. DOI:10.1071/EG998035 |
| [20] | Yin C C, Smith R S, Hodges G, et al. Modeling results of on- and off-time B and dB/dt for time-domain airborne EM systems. 70th Annual Conference and Exhibition, EAGE, 2008. 1~4 |
| [21] | 嵇艳鞠, 林君, 关珊珊, 等. 直升机航空TEM中心回线线圈姿态校正的理论研究. 地球物理学报 , 2010, 53(1): 171–176. Ji Y J, Lin J, Guan S S, et al. Theoretical study of concentric loop coils attitude correction in helicopter-borne TEM. Chinese J. Geophys. (in Chinese) , 2010, 53(1): 171-176. |
| [22] | 朱凯光, 林君, 韩悦慧, 等. 基于神经网络的时间域直升机电磁数据电导率深度成像. 地球物理学报 , 2010, 53(3): 743–750. Zhu K G, Lin J, Han Y H, et al. Research on conductivity depth imaging of time domain helicopter-borne electromagnetic data based on neural network. Chinese J. Geophys. (in Chinese) , 2010, 53(3): 743-750. |
 2011, Vol. 54
2011, Vol. 54