2. 中国科学院地质与地球物理研究所,北京 100029
2. Institute of Geology and Geophysics, Chinese Academy of Sciences, Beijing 100029, China
20 世纪50 年代初提出的大地电磁测深法(Magneto-Telluric, MT)[1, 2]具有探测深度大、成本低、应用范围广等优点,得到了快速发展和广泛应用.但由于MT 法使用的天然场源随机性较大,信号微弱,易受到其他电磁干扰,特别是随着工业化的发展,各种干扰越来越强,严重影响到MT 的探测效果.可控源音频大地电磁法(Controlled Source Audio-Frequency Magnetotellurics, CSAMT)[3]是在大地电磁法的基础上发展起来的一种人工可控源电磁测深法,弥补了天然场源大地电磁法的不足.在20世纪70年代提出来之后即吸引了大量的理论及应用研究,该方法在煤田、找矿、地热、工程等方面得到了广泛的应用,已经成为一种不可或缺的电磁勘探手段[4~23].但是它也存在一些缺点,例如探测深度较浅、源的野外布设较麻烦等,并且这些缺点都是 CSAMT 方法本身所难以克服的,这使得CSAMT法在很多情况下已经不能再满足人们的需求.于是结合了MT 与CSAMT 两者优点的人工源极低频探地电磁法(WEM 方法)应运而生[24~30].
极低频探地电磁法是利用很强的人工发射信号,探测地下深至10km 左右范围内电性细结构的新方法,是地球物理学和无线电物理学相结合的产物[24~31].它在具有一定厚度高阻层的地区铺设超长发射电极距(几十公里)的电缆,大功率(大于500kW)发射0.1~300Hz的电磁波,在数千公里范围内接收该电磁信号以达到深部探测的目的.该技术的特点是信号强度大,抗干扰能力强,信号稳定,测量误差小,覆盖范围广,可配多部接收机大面积组网同时观测,补充了现有天然源大地电磁法(MT)接收信号弱、易受干扰的缺点,同时又补充了人工可控源音频电磁法(CSAMT)设备笨重、探测深度浅(1~2km)、覆盖范围小的缺点,是MT 和CSAMT 方法的改进[24~30].
极低频探地电磁法将为我国地下资源和海洋资源探测、地震预报、气象预报、空间物理研究、地球圈层结构以及各圈层之间的相互作用和耦合关系等前沿科学技术研究提供一种全新的技术手段,是我国地下资源探测和地震预测方法重大的技术创新,具有重大的科学技术价值和现实的使用价值[24~31].
极低频探地电磁法带来了新的问题.对于人工源大功率电磁技术,它的收发距很远甚至可以大于电离层的高度,从而在进行资料分析解释时必须要考虑到电离层的影响,同时,由于可在全国范围内接收信号,使得收发距可达几千公里,此时位移电流的影响不可忽略,采用常规的固体层状地球半空间模型的CSAMT 理论将不再满足需要[27, 29, 30].
极低频探地电磁法正演问题实际上就是研究电离层-空气层-地球介质(称为“地-电离层"模式)耦合下的有源电磁场正演问题[24~27, 29, 30].这是一个新的问题,本文试图将常规的固体层状地球半空间模型的电磁场1D 正演模拟技术,推广到包含电离层、空气层和固体地球层的“地-电离层"模式.
近年来,国内从多个方面开始了极低频电磁波的研究,赵国泽和卓贤军等[24~26]对极低频探地电磁法做了介绍和在地震预报中的应用的研究;柳超[32, 33]和谢慧[34]等做了极低频电磁波发射系统的研究;柳超[35]、王海强[36, 37]、潘威炎[38] 和王元新[39~41]等在极低频电磁波的传播方面做了大量的研究;葛勤革等[42]做了极低频电磁波的干扰性能分析;黄文耿等[43]做了极低频电磁波与低电离层相互作用的研究;卢新城等[44, 45]做了海水中极低频电磁波的传播研究;底青云等[27, 29]做了“地-电离层"模式长发射距大功率可控源电磁波传播研究,即考虑电离层-大气层-固体地球层耦合情况下电磁波的传播的研究.
总体来说,国内外大部分研究是无线电物理领域的,与地球物理专业相关不大,与地球物理相关的研究中涉及到场强计算公式推导的较少,作者实现了当地球层为均匀半空间的正演[30],但实际上地球并不是均匀半空间.本文在此基础上,给出“地-电离层"模式地球多层模型的正演结果.
极低频探地电磁法是一种新的地球物理方法.本文通过研究“地-电离层"模式一维正演,得到“地-电离层"模式多层地球介质模型的电磁波场特征,为进一步弄清极低频探地电磁法探测地下电性细结构的理论基础、提高极低频探地电磁法勘探的分辨率技术的研究、仪器开发、数据处理和最佳测量装置制定具有重要的理论意义和现实意义.
2 模型的建立及公式推导 2.1 模型的建立当研究的深度不是很大(2000km 以内)的情况下,在超低频-极低频段进行深部研究时,可以忽略地球的球面特征,而把它当成一个平面来看待[31].根据文献[46]的计算结果,平板模型和球状模型的场强计算差异主要在收发距大于地球半径以后体现出来,收发距小于地球半径时,其差异甚至可以忽略不计.本文的研究深度远远小于2000km, 收发距最大值为5000km, 小于地球半径,因此采用平板模型来开展研究.
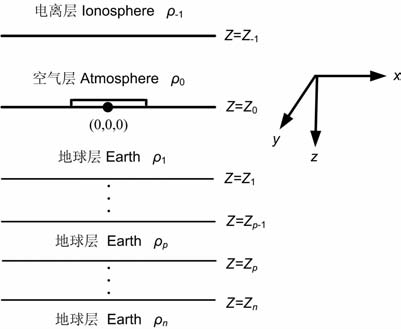
建立的模型如图 1 所示.电离层设为第-1层,空气层为0层,源放置在空气层中,距离地表高度为h0.坐标系的原点设置在源的中心点正下方的地表,z向下为正,向上为负,故电离层的高度为负数.假设电离层和大地层的最底层的厚度为无限.
|
图 1 “地-电离层"模型示意图 Fig. 1 The sketch map of “earth-ionosphere" mode |
模型中电离层底界面的有效高度,也就是空气层的厚度为100km, 电离层的有效电阻率取为1×104 Ωm.每一层的相对介电常数ε,相对磁导率μ 均设为1.
2.2 计算公式在距离地表h0 高度处放置一水平电偶源,供以谐变电流
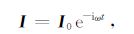
|
(1) |
引入矢量位A后,其基本方程为
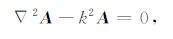
|
(2a) |
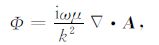
|
(2b) |
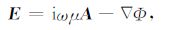
|
(2c) |
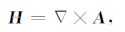
|
(2d) |
式中:A为矢量位;Φ 为标量位;E表示电场矢量;H表示磁场矢量;μ 为导磁率,i表示纯虚数;ω 为圆频率;k2 =-iωμ/ρ-ω2εμ.由于电偶极子沿x方向,水平层状地层介面附近的积累电荷沿z方向,故矢量位只有x方向和z方向分量Ax,Az.利用边界条件
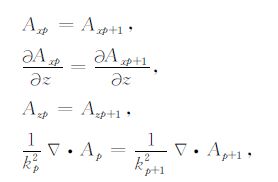
|
(3) |
式中p=-1,0,1,…,n-1,为各层层序.
经过一系列推导,可求得Ax,Az
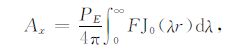
|
(4) |
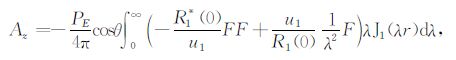
|
(5) |
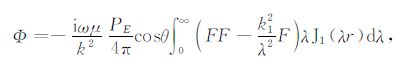
|
(6) |
其中

|
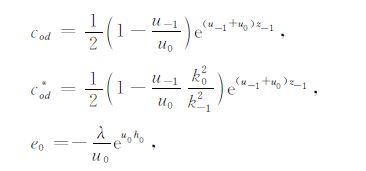
|
式中,up2=λ+k2p;λ 为空间频率;kp是第p层的波数;θ为收发距与x轴的夹角;PE=Idl,I为发射电流,dl为偶极长度;r为收发距,即观测点距偶极子中心的距离;J1(λr)、J0(λr)分别是以λr为变量的一阶、零阶贝塞尔函数;R1 和R1* 为联系各层物性的两个函数,它们和各个电性层的电导率、层厚有关,在地表的具体表达式如下:
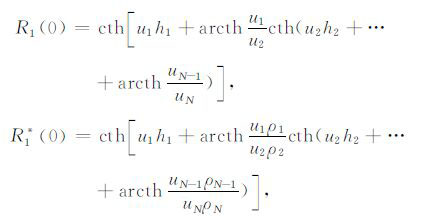
|
(7) |
式中,hp=zp-zp-1,为第p层的厚度,ρp为第p层的电阻率.
本文虽然考虑了电离层的影响,但R函数是由最底层向上推导的,所以推导过程和CSAMT 是一致的[19~22, 47],R函数在地表的表达式也与CSAMT一致.
由(2c)式可求得
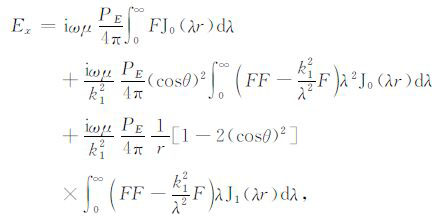
|
(8) |
由(2d)式可求得
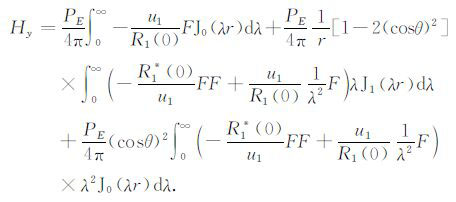
|
(9) |
“地-电离层"模式和CSAMT 的计算公式的主要差异在系数cod和cod*,它们体现了电离层对场强的影响.如果不考虑电离层和空气中位移电流的影响,同时,k0 =0,这时cod和cod*等于0,(8)和(9)式经过化简后,和CSAMT的计算公式[19~22, 47]是一样的.
3 数值计算方法的选择由(8)和(9)式可见,电磁场表达式中含有零阶和一阶Bessel函数的无穷积分,这类积分实质上都是 Hankel变换式[19, 47].由于Bessel函数是振荡衰减函数,且积分区间为无穷,如何计算Bessel积分是电磁法的一个基本问题.由于Bessel函数的振荡性,同时由于积分核函数的振荡性,一般的数值积分方法很难奏效,目前主要采用数字滤波方法,但经过适当的变换,也可以采用数值积分方法实现.20 世纪70年代初发展起来的快速Hankel变换[48~52]方法是计算这类积分最有效的工具之一,本文选择该方法来进行数值计算.
3.1 电磁场的计算公式本文采用的Hankel 滤波系数算法是基于 Johansen[48]优化滤波算法,选取采样密度(抽样间隔Δ=ln10/100),计算得到2040 点高采样密度的滤波系数[53].这样高的采样密度,能够保留足够的高频振荡信息,提高算法的精度.
根据Hankel变换理论[19, 47],将(8)和(9)式改写为如下计算公式:

|
(10) |
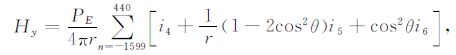
|
(11) |
式中
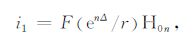
|
(12) |

|
(13) |
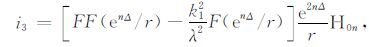
|
(14) |
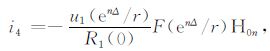
|
(15) |
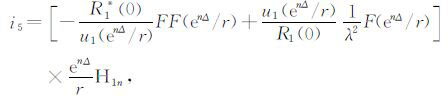
|
(16) |
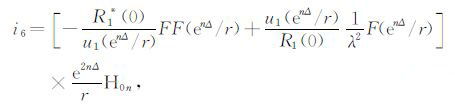
|
(17) |
式中,H0n和H1n分别为第n点的零阶和一阶Hankel滤波系数.
前面关于极低频探地电磁法的介绍中谈到,收发距可能达到数千公里,这时候由于(8)和(9)式中的空间频率λ 具有收发距离倒数的量纲,将会非常小,要求滤波横坐标的最小值非常小.我们采用的抽样间隔为Δ=ln10/100,n取值范围:-1599~440,所以,滤波横坐标范围为:1.0×10-16~25118,完全满足了要求.
3.2 Hankel滤波系数有效性验证对于电磁场正演表达式的数值计算,其收敛性由其无穷积分中的核函数和Bessel函数性质所决定.在CSAMT 正演中,这类积分核是渐增的,而 Bessel函数随宗量的增大是振荡衰减的,其收敛速度较慢,因此导致这类积分的数值计算收敛速度较慢,甚至在某些情况下不收敛(如垂直磁偶极子的磁场水平分量).为了改善这类积分中核函数的特性,提高有限滤波长度下的计算速度和精度,目前在 CSAMT 正演中广泛采用从积分核中减去均匀半空间场表达式中相应的核函数,最后在计算结果中加上相应的解析解[19].
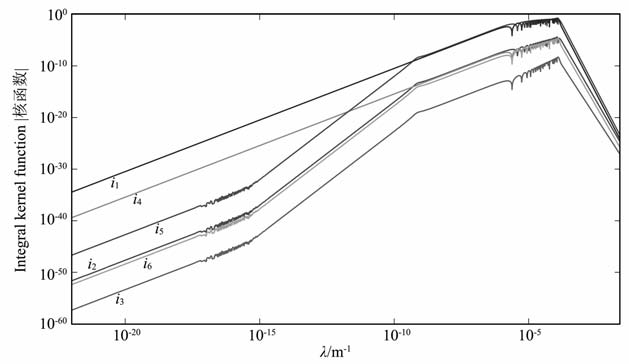
在“地-电离层"模式中,没有相应的地球为均匀半空间的解析解,而且“地-电离层"模式考虑了位移电流的影响,而CSAMT 中并没有考虑,导致核函数的振荡特性发生改变.所以,CSAMT 正演中所采用的这种方法并不能借用,需要寻找其他的方法.本文尝试不处理积分核函数,进行直接积分,直接考察积分核函数i1,i2,i3,i4,i5,i6 是否收敛.
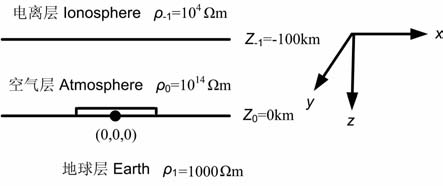
建立了“地-电离层"模式三层模型如图 2所示,设收发距r=100km, 频率为1024Hz, 计算了轴向模式时各核函数与空间频率λ 的函数关系曲线实例(图 3).由图 3可以看出,所有积分核函数都随空间频率λ 的增加表现为有限宽度内的单峰曲线,并且快速收敛,说明数值积分是有效的.
|
图 2 “地-电离层"模式三层模型示意图 Fig. 2 The three layers sketch map of “earth-ionosphere" model |
|
图 3 积分核函数计算结果 Fig. 3 Numerical integration results of integral kernel function by Hankel digital filters |
正演理论是频率域电磁测深理论分析和实际资料处理解释的依据.虽然作者给出了“地-电离层"模式三层模型的正演[30],但是地球不可能是一层的,所以有必要进行“地-电离层"模式多层地球介质的正演模拟.
4.1 水平大地二层模型计算结果为认识“地-电离层"模式地球介质两层断面电磁场特征,建立“地-电离层"模式地球介质两层断面模型如图 4所示.

|
图 4 “地-电离层"模式地球介质两层断面示意图 Fig. 4 The two layers earth model sketch map of “earth-ionosphere" mode |
定义电离层为介质-1,空气层为介质0,地球层为介质1和2.模型电阻率分别为ρ-1=104 Ωm、ρ0=1014 Ωm.各层的厚度h-1 = ∞ 、h0 =100km、h1=1000m、h2=∞.G 型断面时ρ1=100Ωm、ρ2=1000Ωm;D 型断面时ρ1=1000Ωm、ρ2=100Ωm.AB的长度为50km, 发射电流I为200 A,计算时简化为电偶极子.发射的频率系列为f=2nHz, n=-3.5~9.5,间隔为0.5.
测量点位于地表,收发距r分别为100,200,400,800,1600km, 对该模型进行了轴向和赤道装置的电磁波数值模拟.
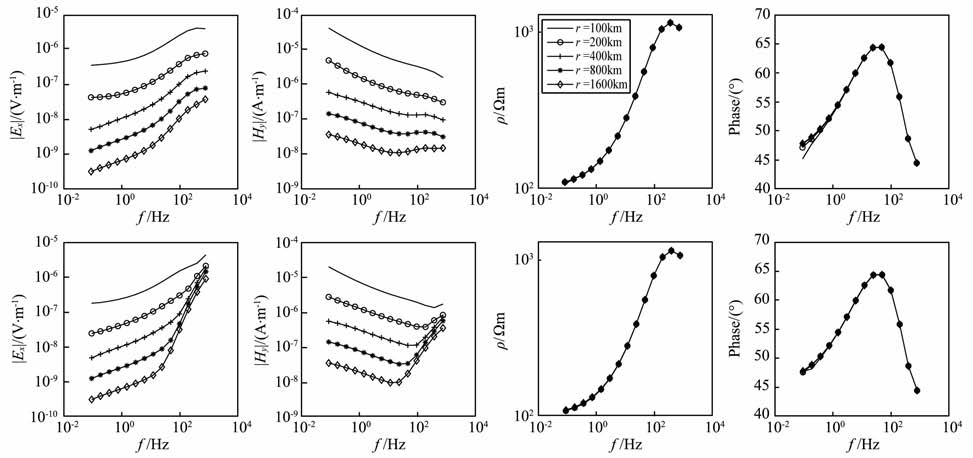
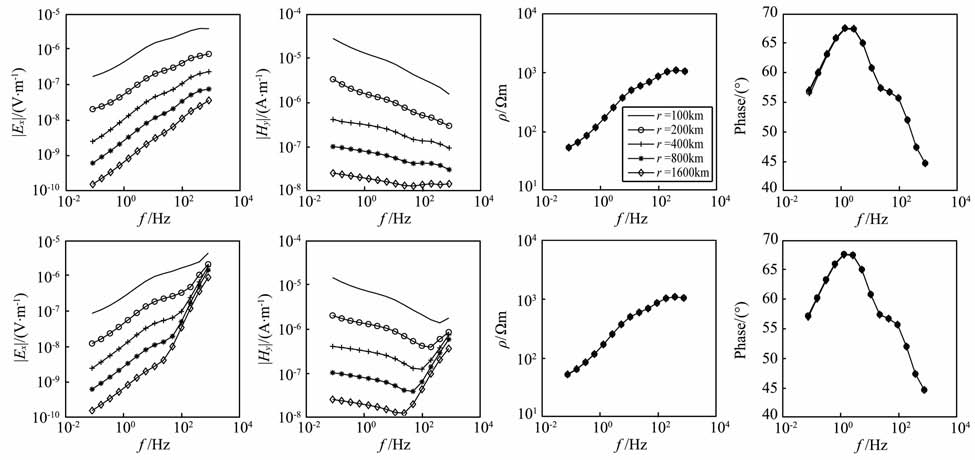
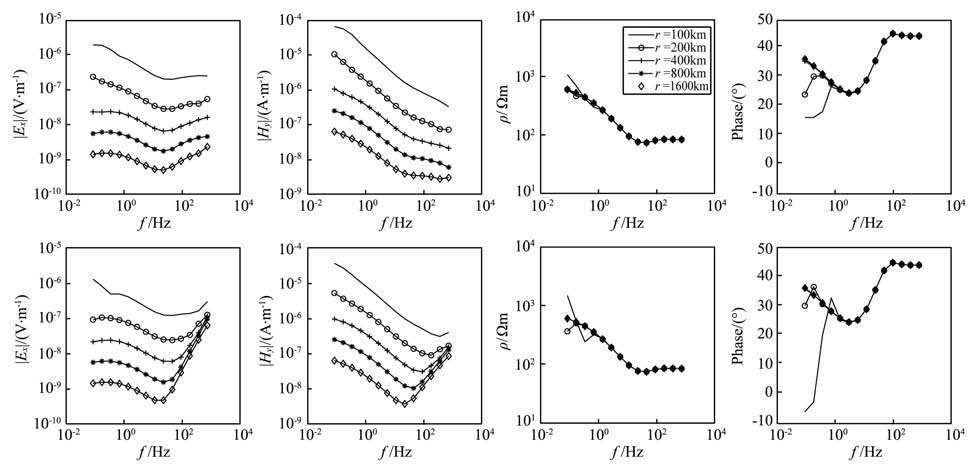
4.1.1 地球介质G 型断面地球介质G 型断面的“地-电离层"模式正演曲线如图 5所示,第一行为赤道装置,第二行为轴向装置.可以看出,在高频段,两种装置受位移电流影响有差异,主要体现在轴向装置的高频段的场值比赤道装置的要大;从视电阻率和相位曲线看,两种装置都明显地反映了高低阻的情况;在r=100km 时,轴向装置的“Undershoot"现象要比赤道装置的明显.
|
图 5 地球介质G 型断面不同收发距的Ex、Hy、ρxy、相位频率响应曲线 (第一行:赤道装置;第二行:轴向装置) Fig. 5 Frequency response curves of Ex,Hy,ρxy,phase in different offset for G-type earth model (First row: equatorial array; Second row: axial array) |
“Undershoot"现象也就是假极值现象,它是自然界中许多情况下能够见到的一种普遍的物理现象,即一个物理量从低值突然升高到高值时,往往在向高值转折之前,先向下冲一下,然后再继续上升,类似于“反弹"效应,具体到电磁法是由于分界面上下的阻抗不同所产生的向上传播的电磁波与入射电磁波的干涉引起的.基底的阻抗越大,电磁波的吸收作用就越弱,“Undershoot"效应越明显,且轴向方向的电场在过渡带中的“Undershoot"更明显[47],因此导致轴向装置的“Undershoot"现象比赤道装置的明显.
当收发距r大于200km 时,两种装置的视电阻率曲线在低频段都接近地球介质第二层的真实电阻率.
4.1.2 地球介质D 型断面地球介质D 型断面的“地-电离层"模式正演曲线如图 6所示.地球介质D 型断面的“地-电离层"模式正演曲线和G 型类似,在高频段,两种装置受位移电流影响有差异,主要体现在轴向装置的高频段的场值比赤道装置的要大,这种差异随着收发距的加大而越加明显;从视电阻率和相位曲线看,两种装置都明显地反映了高低阻的情况;视电阻率曲线在低频段都接近地球介质第二层的真实电阻率.由于 D 型断面中,基底的阻抗较小,电磁波的吸收作用较强,所以“Undershoot"效应不明显.
4.2 水平大地三层模型计算结果建立“地-电离层"模式地球介质三层断面模型如图 7所示,定义电离层为介质-1,空气层为介质0,地球层为介质1、2和3.模型电阻率分别为ρ-1=104 Ωm、ρ0=1014 Ωm, H 型断面时ρ1=1000 Ωm、ρ2=250Ωm、ρ3=4000Ωm;K 型断面时ρ1=1000Ωm、ρ2=4000Ωm、ρ3=1000Ωm;A型断面时ρ1=1000Ωm、ρ2=4000Ωm、ρ3=32000Ωm;Q型断面时ρ1=1000Ωm、ρ2=250Ωm、ρ3=31.25Ωm.各层的厚度h-1=∞、h0=100km、h1=1000m、h2=2000m、h3=∞.
|
图 7 “地-电离层"模式地球介质三层断面示意图 Fig. 7 The three layers earth model sketch map of “earth-ionosphere" mode |
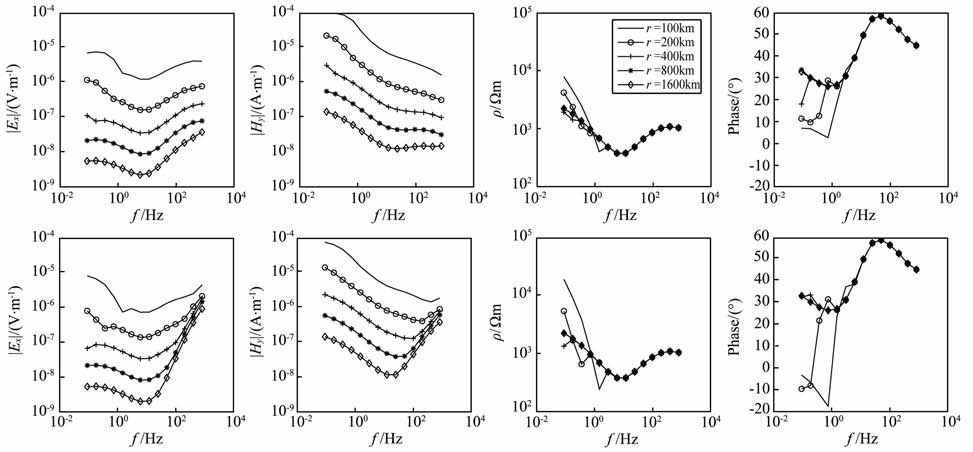
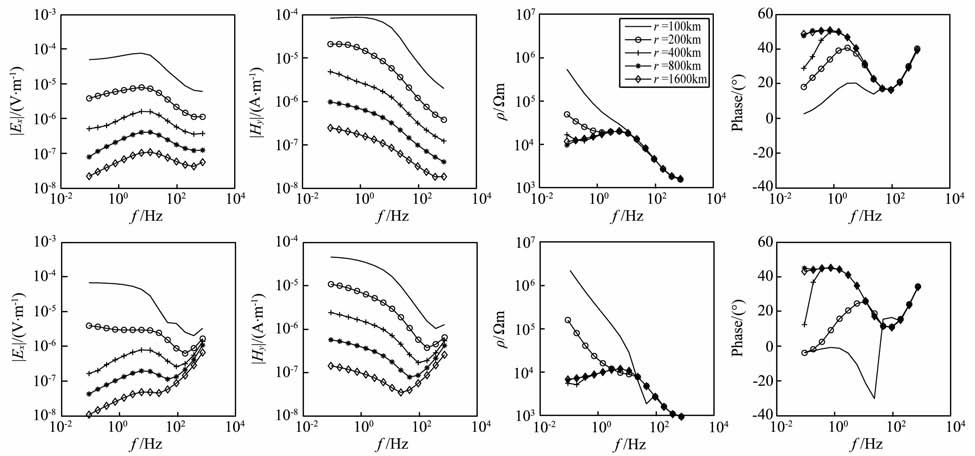
地球介质H 型断面的“地-电离层"模式正演曲线如图 8所示.在高频段,两种装置受位移电流影响有差异,轴向装置的高频段的场值比赤道装置的要大,这种差异随着收发距的加大而越加明显;H 型断面中,基底的阻抗较大,电磁波的吸收作用较弱,所以“Undershoot"效应明显;两种装置从相位曲线上都明显地反映了高阻-低阻-高阻的情况;当收发距r>400km 后,两种装置的视电阻率曲线在低频段都接近地球介质第3层的真实电阻率.
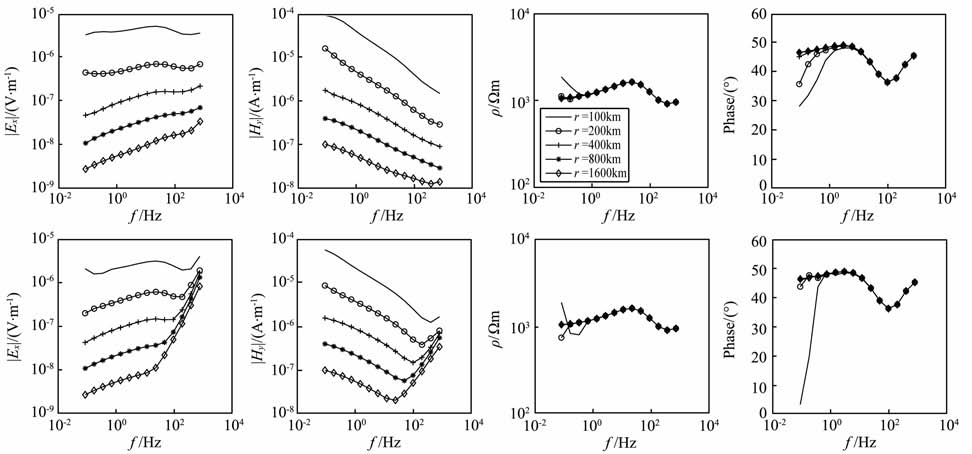
地球介质K 型断面的“地-电离层"模式正演曲线如图 9所示.在高频段,两种装置受位移电流影响有差异,轴向装置的高频段的场值比赤道装置的要大;当收发距r=100km 时,两种装置在低频段出现了近场效应,且轴向装置的“Undershoot"现象要比赤道装置的明显;两种装置从相位曲线上都明显地反映了低阻-高阻-低阻的情况;当收发距r>400km后,两种装置的视电阻率曲线在低频段都接近地球介质第3层的真实电阻率.
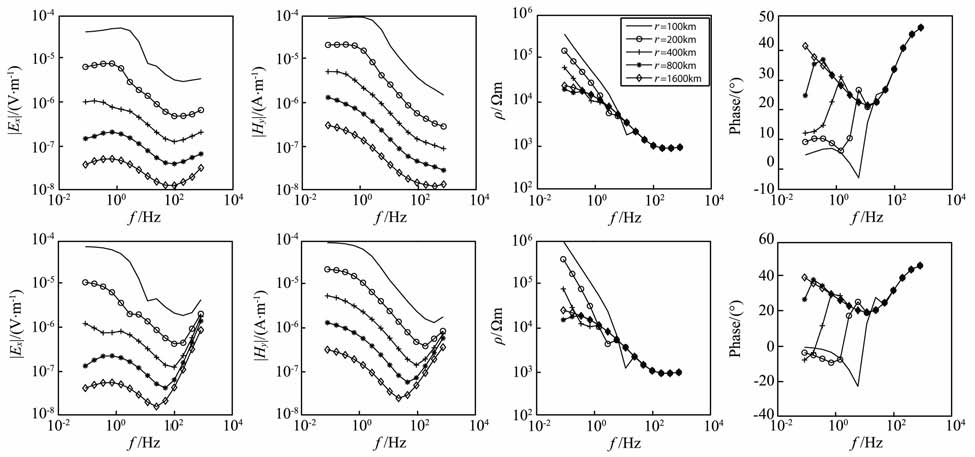
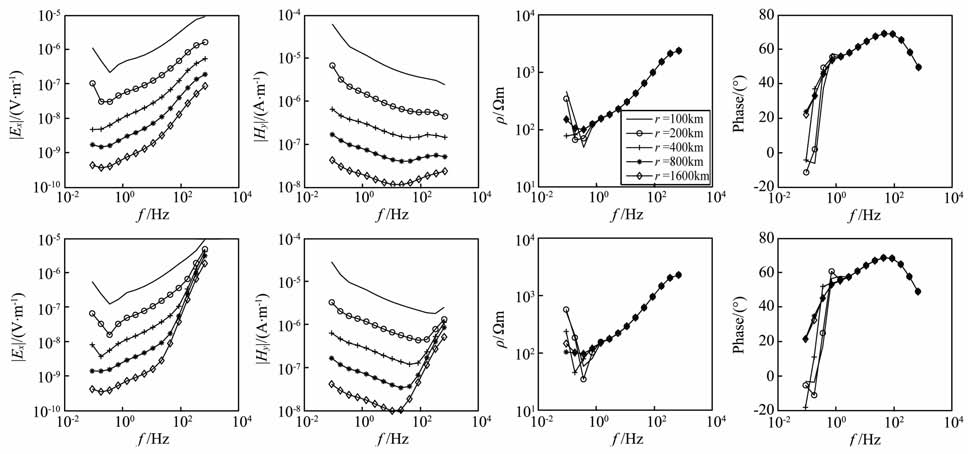
4.2.2 地球介质A 型断面地球介质A 型断面的正演曲线如图 10 所示.在高频段,两种装置受位移电流影响有差异,轴向装置的高频段的场值比赤道装置的要大;由于A 型断面基底的阻抗大,电磁波的吸收作用较弱,所以“Undershoot"效应明显,从视电阻率和相位曲线看,当收发距r<800km 时,两种装置在低频段都出现了近场效应,且赤道装置进入近场的频率要更高;轴向装置的“Undershoot"现象要比赤道装置的明显;两种装置从视电阻率和视相位曲线上都较难反映中间层的电阻率情况,说明“地-电离层"模式和 CSAMT 类似,存在等值效应,对电阻率连续变化的中间层难以辨认.除了r=1600km 外,两种装置其他收发距上的视电阻率和视相位曲线在低频段都出现了近场效应,这跟最底层的电阻率太高是有关的.
4.2.3 地球介质Q 型断面地球介质Q 型断面的正演曲线如图 11 所示.在高频段,两种装置受位移电流影响有差异,轴向装置的高频段的场值比赤道装置的要大;从视电阻率和相位曲线看,由于地球介质的底层电阻率很低,两种装置的曲线很难看出区别;两种装置从相位曲线上较难反映中间层的电阻率情况,说明“地-电离层"模式和CSAMT 类似,存在等值效应,对电阻率连续变化的中间层难以辨认.
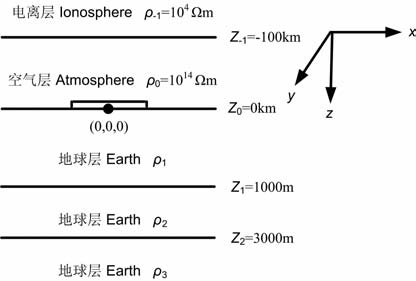
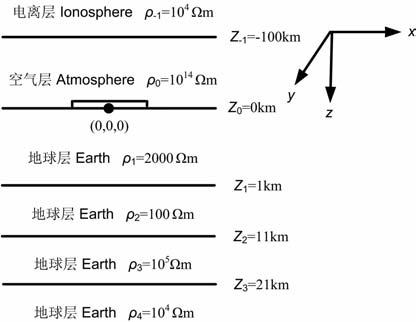
4.3 地盾模型计算结果参考文献[27],建立如图 12含三层地球介质的地盾模型,在1km 深处有一厚度为20km 电阻率为105 Ωm 的导电性不好的中间层,也就是较常见的地电断面结晶地盾.定义电离层为介质-1,空气层为介质0,地球层为介质1、2、3.模型电阻率分别为ρ-1=104 Ωm、ρ0=1014 Ωm、ρ1=2000Ωm, ρ2=105 Ωm, ρ3 =104 Ωm.各层的厚度h-1 = ∞,h0 =100km, h1=1km, h2=20km, h3=∞.
|
图 12 “地-电离层"模式地盾模型 Fig. 12 The continental shield model sketch map of “earth-ionosphere" mode |
结果(图 13)表明,对于地盾模型,轴向和赤道模式的电场Ex、磁场Hy的频率响应,随着收发距离的增加都存在一些变化,变化最大的是收发距在100km 和200km 时,当收发距离进一步增大时,低频段除了场的幅值持续减小外,频率响应曲线形态的趋势基本是一致的.高频段也出现了Ex和Hy随着频率的增加而增加,收发距越大,Ex和Hy随频率的增加就越快.而且这种场强随频率增加而增加的现象轴向模式要比赤道模式更明显.但无论是轴向还是赤道模式的场都能反映出中间导电性不好的结晶地盾层的存在.对于收发距为100km 和200km的情况,频率低于25 Hz时,视电阻率曲线迅速上翘,这是近场效应,并且轴向模式出现近场效应的频率要高于赤道模式.本文和文献[27]的计算结果有一定的差异,主要体现在高频段,本文较文献[27]的场强要更大,而且轴向装置的差异更大,原因是本文考虑了空气中位移电流的影响,而文献[27]则没有考虑空气中位移电流的影响.
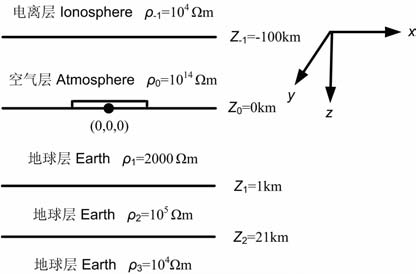
4.4 地台模型计算结果参考文献[27],建立含四层地球介质的“地-电离层"地台模型,模型的电阻率和层厚参数见图 14.定义电离层为介质-1,空气层为介质0,地球层为介质1、2、3、4.模型电阻率分别为ρ-1=104 Ωm、ρ0=1014 Ωm、ρ1=2000Ωm、ρ2=100Ωm、ρ3=105 Ωm、ρ4=104 Ωm.各层的厚度h-1 = ∞、h0 =100km、h1=1km、h2=10km、h3=10km、h4= ∞.计算参数与4.1节中的相同.
|
图 14 “地-电离层"模式地台模型 Fig. 14 The platform model sketch map of “earth-ionosphere" mode |
图 15展示了地台模型在距源中心分别为100、200、400、800km和1600km时轴向和赤道模式的电场Ex、磁场Hy、视电阻率ρxy和视相位的频率响应曲线.
由于受中间低阻层的影响,电场分量、磁场分量、电阻率和相位曲线特征完全不同于地盾模型的场的特征,但场随偏移距的变化规律是相同的.可以清楚地看出,无论是轴向还是赤道模式的场都能很好地反映出中间良导层的存在.同样对于小收发距100km 和200km 的电阻率曲线低频时出现了近场响应,表现出上翘特征.低频段除了场的幅值持续减小外,频率响应曲线形态的趋势基本是一致的.但高频段也出现了Ex和Hy随着频率的增加而增加,收发距越大,Ex和Hy随频率的增加就越快.而且这种场强随频率增加而增加的现象轴向模式要比赤道模式更明显,赤道模式的反映不是很明显,与椭圆极化的特征对应.本文和文献[27]的计算结果有一定的差异,主要体现在高频段,本文较文献[27]的场强要更大,而且轴向装置的差异更大,原因是本文考虑了空气中位移电流的影响,而文献[27]则没有考虑空气中位移电流的影响.
5 结论本文进行了“地-电离层"模式大功率可控源的1D 电磁波正演研究.建立了“地-电离层"模式层状地球表面水平电偶源形成的谐变场的地质和数学模型,利用R函数法进行了“地-电离层"模式的公式推导,得出“地-电离层"模式地球表面水平电偶源的地表场强表达式.
采用高采样密度的Hankel滤波实现数值模拟,在证实数值模拟方法有效前提下,进行了“地-电离层"模式地球介质两层、三层、四层和地盾、地台模型的正演.
总的来说,无论是哪一种模型,在收发距为800km和1600km 时,电场和磁场分量随频率的增加而快速增加,并且收发距越大,频率越低,这种增加可以解析为受位移电流的影响,轴向装置的这种现象比赤道装置的要明显很多,这体现了两个方向的电磁波场衰减速度不等,轴向装置的衰减速度更慢.
除了A 型断面由于最底层的电阻率太大,而在收发距r=200km 时进入近场的频率较高外,其他的断面类型的视电阻率曲线大部分是相互重叠的,这表明在收发距r>200km 后,所研究的频段基本上满足波区条件的.所有断面的视相位曲线都能很好地反映地球介质的高低阻情况,这与MT 和 CSAMT 法是相同的.
A 型和Q 型断面的视电阻率曲线对中间层参数反映不明显,即具有全等值现象,说明“地-电离层"模式和其他的电磁测深方法一样,对具有连续上升趋势的断面的中间高阻层薄层是几乎无能无力的.数值模拟结果表明,本文的计算结果与文献[27]中的结果在高频段有较大的差异,原因是文献[27]没有考虑空气中位移电流的影响.文中的理论分析部分已经得出结论,必须考虑空气中位移电流的影响.
致谢感谢中国科学院地质与地球物理研究所王光杰、王若老师的指点,感谢吉林大学郑圣谈提供的帮助,同时感谢中国科学院地质与地球物理研究所安志国、付长民、程辉、岳安平、许诚、程勃博士以及薛融晖、张永超硕士卓有成效的讨论.两位评审人所提出的修改意见非常细致、中肯,对本文的完善起到了重要作用,在此表示诚挚的感谢!
| [1] | Tikhonov A N. On determining electrical characteristics of the deep layers of the Earth's crust. Dok1. Akad. Nauk. SSSR , 1950, 73(2): 295-297. |
| [2] | Cagniard L. Basic theory of the magneto-telluric method of geophysical prospecting. Geophysics , 1953, 18(3): 605-635. DOI:10.1190/1.1437915 |
| [3] | Goldstein M A, Strangway D W. Audio-frequency magnetotellurics with a grounded electric dipole source. Geophysics , 1975, 40(4): 669-683. DOI:10.1190/1.1440558 |
| [4] | Basokur A T, Rasmussen T M, Kaya C, et al. Comparison of induced polarization and controlled-source audio-magnetotellurics methods for massive chalcopyrite exploration in a volcanic area. Geophysics , 1997, 62(4): 1087-1096. DOI:10.1190/1.1444209 |
| [5] | Zonge K L, Hughes L J. Controlled source audio-frequency magnetotellurics. In: Nabighian M N, ed. Electromagnetic Methods in Applied Geophysics. 1991,2(Part B): 713~809 |
| [6] | Zonge K L, Ostrander A G, Emer D F. Controlled-source audio-frequency magnetotelluric measurements. In: Vozoff K, ed. Magnetotelluric Methods. Society of Exploration Geophysicists, 1986, 5: 749~763 |
| [7] | Sandberg S K, Hohmann G W. Controlled-source audio-frequency magnetotellurics in geothermal exploration. Geophysics , 1982, 47(1): 100-116. DOI:10.1190/1.1441272 |
| [8] | 王光杰, 王勇, 李帝铨, 等. 基于遗传算法CSAMT反演计算研究. 地球物理学进展 , 2006, 24(4): 1285–1289. Wang G J, Wang Y, Li D Q, et al. The application of Genetic Algorithm to CSAMT inversion. Progress in Geophysics (in Chinese) , 2006, 24(4): 1285-1289. |
| [9] | 刘红涛, 杨秀瑛, 于昌明, 等. 用VLF、EH4和CSAMT方法寻找隐伏矿——以赤峰柴胡栏子金矿床为例. 地球物理学进展 , 2004, 19(2): 276–285. Liu H T, Yang X Y, Yu C M, et al. A case study in finding concealed ores by using geophysical exploration methods in combination of VLF-EM, EH4 and CSAMT. Progress in Geophysics (in Chinese) , 2004, 19(2): 276-285. |
| [10] | 底青云, 王妙月, 石昆法, 等. V6多功能系统及其在CSAMT勘查应用中的效果. 地球物理学进展 , 2002, 17(4): 663–670. Di Q Y, Wang M Y, Shi K F, et al. Multifunction system-V6 and its effectiveness in CSAMT exploration. Progress in Geophysics (in Chinese) , 2002, 17(4): 663-670. |
| [11] | 底青云, 王妙月. 煤层上覆地层含水不均匀性电法探测的可能性. 地球物理学进展 , 2003, 18(4): 707–710. Di Q Y, Wang M Y. Prospecting possibility with electric method for thin water-bearing rock layer upper the coal layers. Progress in Geophysics (in Chinese) , 2003, 18(4): 707-710. |
| [12] | 底青云, 石昆法, 王妙月, 等. CSAMT法和高密度电法探测地下水资源. 地球物理学进展 , 2001, 16(3): 53–58. Di Q Y, Shi K F, Wang M Y, et al. Water resources exploration with CSAMT and high density electric resistivity method. Progress in Geophysics (in Chinese) , 2001, 16(3): 53-58. |
| [13] | 于昌明. CSAMT方法在寻找隐伏金矿中的应用. 地球物理学报 , 1998, 41(1): 133–138. Yu C M. The application of CSAMT method in looking for hidden gold mine. Chinese J. Geophys. (Acta Geophysica Sinica) (in Chinese) , 1998, 41(1): 133-138. |
| [14] | 吴璐萍, 石昆法, 李荫槐, 等. 可控源音频大地电磁法在地下水勘查中的应用研究. 地球物理学报 , 1996, 39(5): 712–717. Wu L P, Shi K F, Li Y H, et al. Application of CSAMT to the search for groundwater. Chinese J. Geophys. (Acta Geophysica Sinica) (in Chinese) , 1996, 39(5): 712-717. |
| [15] | 王若, 底青云, 王妙月, 等. 用积分方程法研究源与勘探区之间的三维体对CSAMT 观测曲线的影响. 地球物理学报 , 2009, 52(6): 1573–1582. Wang R, Di Q Y, Wang M Y, et al. Research on the effect of 3D body between transmitter and receivers on CSAMT response using Integral Equation method. Chinese J. Geophys. (in Chinese) , 2009, 52(6): 1573-1582. |
| [16] | 李帝铨, 王光杰, 底青云, 等. 基于遗传算法的CSAMT最小构造反演. 地球物理学报 , 2008, 51(4): 1234–1245. Li D Q, Wang G J, Di Q Y, et al. The application of Genetic Algorithm to CSAMT inversion for minimum structure. Chinese J. Geophys. (in Chinese) , 2008, 51(4): 1234-1245. |
| [17] | 底青云, 王妙月, 石昆法, 等. 高分辨率V6系统在矿山顶板涌水隐患中的应用研究. 地球物理学报 , 2002, 45(5): 744–748. Di Q Y, Wang M Y, Shi K F, et al. An applied study on prevention of water bursting disaster in mines with the high resolution V6 system. Chinese J. Geophys. (in Chinese) , 2002, 45(5): 744-748. |
| [18] | 底青云, 王光杰, 安志国, 等. 南水北调西线千米深长隧洞围岩构造地球物理勘探. 地球物理学报 , 2006, 49(6): 1836–1842. Di Q Y, Wang G J, An Z G, et al. Geophysical exploration of a long deep tunnel on the west route of South-to-North Water Diversion Project. Chinese J. Geophys. (in Chinese) , 2006, 49(6): 1836-1842. |
| [19] | 汤井田, 何继善. 可控源音频大地电磁法及其应用. 长沙: 中南大学出版社, 2005 . Tang J T, He J S. Theory and Application of CSAMT Method (in Chinese). Changsha: Central South University Press, 2005 . |
| [20] | 石昆法. 可控源音频大地电磁法理论与应用. 北京: 科学出版社, 1999 . Shi K F. Theory and Application of CSAMT Method (in Chinese). Beijing: Science Press, 1999 . |
| [21] | 何继善. 可控源音频大地电磁法. 长沙: 中南工业大学出版社, 1990 . He J S. Control Source Audio-Frequency Magnetotellurics (in Chinese). Changsha: Central South University of Technology Press, 1990 . |
| [22] | 底青云, 王若. 可控源音频大地电磁数据正反演及方法应用. 北京: 科学出版社, 2008 . Di Q Y, Wang R. CSAMT Forward Modeling and Inversion and Its Application (in Chinese). Beijing: Science Press, 2008 . |
| [23] | Nabighian M N. 勘查地球物理 电磁法 第一卷. 赵经祥, 王艳君译. 北京: 地质出版社, 1992. Nabighian M N. Electromagnetic Methods in Applied Geophysics, Volume 1 (in Chinese). Zhao J X, Wang Y J Trans. Beijing: Geological Publishing House, 1992 |
| [24] | 赵国泽, 陆建勋. 利用人工源超低频电磁波监测地震的试验和分析. 中国工程科学 , 2003, 5(10): 27–33. Zhao G Z, Lu J X. Monitoring and analysis of earthquake phenomena by artificial SLF waves. Engineering Science (in Chinese) , 2003, 5(10): 27-33. |
| [25] | 赵国泽, 汤吉, 邓前辉, 等. 人工源超低频电磁波技术及在首都圈地区的测量研究. 地学前缘 , 2003, 10(Suppl.): 248–257. Zhao G Z, Tang J, Deng Q H, et al. Artificial SLF method and the experimental study for earthquake monitoring in Beijing area. Earth Science Frontiers (in Chinese) , 2003, 10(Suppl.): 248-257. |
| [26] | 卓贤军, 赵国泽. 一种资源探测人工源电磁新技术. 石油地球物理勘探 , 2004, 39(Suppl.): 114–117. Zhuo X J, Zhao G Z. A new technique of EM controlled-source sounding for resource prospecting. Oil Geophys.Prosp. (in Chinese) , 2004, 39(Suppl.): 114-117. |
| [27] | 底青云, 王妙月, 王若, 等. 长偶极大功率可控源电磁波响应特征研究. 地球物理学报 , 2008, 51(6): 1917–1928. Di Q Y, Wang M Y, Wang R, et al. Study of the long bipole and large power electromagnetic field. Chinese J. Geophys. (in Chinese) , 2008, 51(6): 1917-1928. |
| [28] | 陈小斌, 赵国泽. 关于人工源极低频电磁波发射源的讨论——均匀空间交流点电流源的解. 地球物理学报 , 2009, 52(8): 2158–2164. Chen X B, Zhao G Z. Study on the transmitting mechanism of CSELF waves: response of the alternating current point source in the uniform space. Chinese J. Geophys. (in Chinese) , 2009, 52(8): 2158-2164. |
| [29] | 底青云, 王光杰, 王妙月, 等. 长偶极大功率可控源激励下目标体电性参数的频率响应. 地球物理学报 , 2009, 52(1): 275–280. Di Q Y, Wang G J, Wang M Y, et al. Frequency response characteristics of target electric property with long bipole large power control source. Chinese J. Geophys. (in Chinese) , 2009, 52(1): 275-280. |
| [30] | 李帝铨, 底青云, 王妙月. 电离层-空气层-地球介质耦合下大尺度大功率可控源电磁波响应特征研究. 地球物理学报 , 2010, 53(2): 411–420. Li D Q, Di Q Y, Wang M Y. Study of large scale large power control source electromagnetic with "Earth-ionosphere" mode. Chinese J. Geophys. (in Chinese) , 2010, 53(2): 411-420. |
| [31] | 国家圣彼得保大学文森-列辛克地壳研究所编写. 地球物理研究及地震预测研究中发射-测量装置的发射系统安装场地选择的技术要求及建议. 2000 |
| [32] | 柳超, 翟琦, 谢慧, 等. 极低频发射天线场地等效视电阻率的计算. 西安电子科技大学学报 (自然科学版) , 2005, 32(4): 584–586. Liu C, Zhai Q, Xie H, et al. A calculating method of the effective apparent resistivity for the extremely low frequency transmitting antenna site. Journal of Xidian University (Natural Science) (in Chinese) , 2005, 32(4): 584-586. |
| [33] | 柳超, 董颖辉. 甚低频发射系统仿真研究. 现代通信技术 , 2001(4): 58–60. |
| [34] | 谢慧, 高俊, 柳超, 等. 超低频拖曳全向接收天线运动感应噪声研究. 电波科学学报 , 2007, 22(5): 861–866. Xie H, Gao J, Liu C, et al. Analysis of motion-induced noise of super low frequency towed omni-directional receive antenna. Chinese Journal of Radio Science (in Chinese) , 2007, 22(5): 861-866. |
| [35] | 柳超. 超低频通信中的辐射场研究. 现代通信技术 , 1993(4): 48–51. |
| [36] | 王海强. 地-电离层波导中的极低频传播. 电波与天线 , 1994(5): 34–37. |
| [37] | 王海强. 各向同性指数地-电离层波导中甚低频传播的近似解. 电波与天线 , 1994(6): 52–60. |
| [38] | 潘威炎. 长波超长波极长波传播. 成都: 电子科技大学出版社, 2002 . |
| [39] | 王元新, 彭茜, 潘威炎, 等. SLF/ELF水平电偶极子在地-电离层波导中的场. 电波科学学报 , 2007, 22(5): 728–734. Wang Y X, Peng Q, Pan W Y, et al. The fields excited by SLF/ELF horizontal electric dipole in Earth-ionosphere cavity. Chinese Journal of Radio Science (in Chinese) , 2007, 22(5): 728-734. |
| [40] | 王元新, 樊文生, 潘威炎, 等. 垂直电偶极子在地-电离层波导中场的球级数解. 电波科学学报 , 2007, 22(2): 204–211. Wang Y X, Fan W S, Pan W Y, et al. Spherical harmonic series solution of fields excited by vertical electric dipole in Earth-ionosphere cavity. Chinese Journal of Radio Science (in Chinese) , 2007, 22(2): 204-211. |
| [41] | 王元新. 极低频在地-电离层波导中传播的新的理论计算方法. 中国电波传播研究所, 2007 |
| [42] | 葛勤革. 超低频通信抗干扰性能分析. 海军工程大学学报 , 2007, 19(5): 62–64. Ge Q G. Analysis of electronic anti-jamming performance of extremely low frequency communications. Journal of Naval University of Engineering (in Chinese) , 2007, 19(5): 62-64. |
| [43] | 黄文耿, 古士芬. 大功率无线电波与低电离层的相互作用. 空间科学学报 , 2003, 23(3): 181–188. Huang W G, Gu S F. Interaction between the powerful high-frequency radio wave and the lower terrestrial ionosphere. Chinese Journal of Space Science (in Chinese) , 2003, 23(3): 181-188. |
| [44] | 卢新城, 龚沈光, 周骏, 等. 海水中极低频水平电偶极子电磁场的解析解. 电波科学学报 , 2004, 19(3): 290–295. Lu X C, Gong S G, Zhou J, et al. Analytical expressions of the electromagnetic fields produced by an ELF time-harmonic HED embedded in the sea. Chinese Journal of Radio Science (in Chinese) , 2004, 19(3): 290-295. |
| [45] | 卢新城, 龚沈光, 周骏, 等. 深海中极低频时谐垂直电偶极子电磁场的解析解. 武汉理工大学学报 (交通科学与工程版) , 2003, 27(6): 746–749. Lu X C, Gong S G, Zhou J, et al. Analytical solutions of electromagnetic fields produced by an ELF time-harmonic VED in deep sea. Journal of Wuhan University of Technology (Transportation Science & Engineering) (in Chinese) , 2003, 27(6): 746-749. |
| [46] | 朴化荣. 电磁测深法原理. 北京: 地质出版社, 1990 . Piao H R. The Principle of Electromagnetic Sounding (in Chinese). Beijing: Geological Publishing House, 1990 . |
| [47] | 卓贤军. 人工源超低频电磁场场强分布及测量的研究. 北京: 中国地震局地质研究所, 2005 . |
| [48] | Johansen H K, Sorensen K. Fast Hankel transforms. Geophysical Prospecting , 1979, 27(4): 876-901. DOI:10.1111/gpr.1979.27.issue-4 |
| [49] | Chave A D. Numerical integration of related Hankel transforms by quadrature and continued fraction expansion. Geophysics , 1983, 48(12): 1671-1686. DOI:10.1190/1.1441448 |
| [50] | Anderson W L. A hybrid fast Hankel transform algorithm for electromagnetic modeling. Geophysics , 1989, 54(2): 263-266. DOI:10.1190/1.1442650 |
| [51] | Christensen N B. Optimized fast Hankel transform filters. Geophysical Prospecting , 1990, 38(5): 545-568. DOI:10.1111/gpr.1990.38.issue-5 |
| [52] | Guizar-Sicairos M, Gutiérrez-Vega J C. Computation of quasi-discrete Hankel transforms of integer order for propagating optical wave fields. Journal of the Optical Society of America A , 2004, 21(1): 53-58. DOI:10.1364/JOSAA.21.000053 |
| [53] | 郑圣谈, 曾昭发, 刘四新, 等. 宽带高频电磁场数据反演方法研究. 地球物理学报 , 2008, 50(1): 266–272. Zheng S T, Zeng Z F, Liu S X, et al. Inversion of the wideband and high frequency electromagnetic data. Chinese J. Geophys. (in Chinese) , 2008, 50(1): 266-272. |
 2011, Vol. 54
2011, Vol. 54