2. 中国人民解放军理工大学气象学院,南京 211101;
3. 中国科学院上海天文台,上海 200030;
4. 温州大学数学与信息科学学院,温州 325027
2. Institute of Meteorology, PLA University of Science and Technology, Nanjing 211101, China;
3. Shanghai Astronomical Observatory, Chinese Academy of Sciences, Shanghai 200030, China;
4. School of Mathematics & Information Science, Wenzhou University, Zhejiang Wenzhou 325027, China
1993年,美国的UCAR(University Corporation for Atmosphere Research)、Arizona 大学和JPL(Jet Propulsion Laboratory)联合制定了首次GPS/LEO(Global Positioning System/Low Earth Orbit)掩星实验---GPS/MET(Meteorology)计划.继GPS/ MET 之后,CHAMP、SAC-C、GRACE、COSMIC 等计划的成功发射,每天可提供几千个中性大气层和电离层的掩星廓线[1].此外,GPS/LEO 掩星还具有高精度、高垂直分辨率、全球覆盖、全天候、长期稳定等特点,这是其他卫星探测手段难以比拟的.
GPS/LEO 掩星指GPS 信号穿过地球大气层后,被安装在LEO 卫星上的GPS接收机接收.接收的信号中包含了大气层和电离层的信息,通过相关的反演方法,可得到高精度的大气层和电离层的参量廓线,包括大气层的折射率、密度、温度、水汽压廓线和电离层的电子密度廓线[2, 3].
在低对流层(尤其是热带区域),水汽含量较为丰富,折射率结构复杂.这不仅会导致GPS 信号急剧衰减,还会发生大气多路径传播,即发射机发出的多个信号通过地球大气后同时到达接收机[4].在大气多路径传播条件下,通过几何光学方法反演多普勒频移(局部测量信息),会出现同一碰撞参数对应多个弯曲角的值.因此必须采用全息反演技术,即利用所有或者某一段的测量信息进行反演.目前比较成熟的全息反演技术包括:后向传播方法[5]、滑动频谱方法[6]、正则变换方法[7]以及全谱反演方法[8].
后向传播方法的思想首先由美国Stanford 大学的Marouf提出,用于旅行者号掩星观测土星和天王星环,结果发现衍射效应明显减弱且径向分辨率得到提高[9].而地球大气,特别是大气边界层中的衍射效应更为复杂,Karayel, Gorbunov, Kursinski等人在后向传播反演地球大气方面做了大量的工作: Karayel指出几何光学方法的垂直分辨率受到第一菲涅耳带直径的限制,后向传播方法能有效地克服这种限制,其所得到的折射率具有更高的垂直分辨率,从而使得掩星探测大气边界层成为可能[10]; Gorbunov通过比较几何光学方法和后向传播方法后发现,后向传播方法能极大地改进数据反演的质量[5];Kursinski对后向传播方法做了进一步的改进,并说明后向传播方法能降低大气多路径效应的影响[4].
本文采用多相位屏模型,数值模拟了大气多路径传播条件下无线电信号在大气中的传播过程.分别用几何光学方法和后向传播方法对模拟信号进行反演,结果验证了后向传播方法的准确性.用上述两种方法对CHAMP掩星数据进行反演,将其折射率与相应的ECMWF(European Centre for Medium- Range Weather Forecasts)分析场进行统计比较.结果表明:后向传播方法降低了大气多路径效应的影响,提高了反演结果的准确性.
本文第2节简单介绍单路径假设下的几何光学方法;第3节阐述后向传播方法;第4节利用多相位屏模型对大气多路径条件下无线电信号的传播过程进行了模拟仿真;第5 节分别用几何光学方法和后向传播方法反演CHAMP掩星观测数据,并将其折射率反演结果与ECMWF 分析场资料进行了统计比较;第6节给出结论和讨论.
2 几何光学方法GPS的观测量主要是频率f1=1575.42 MHz和f2=1227.60 MHz的相位和振幅,在消除周跳和钟差之后,将测量相位减去GPS 与LEO 间直线距离可得到附加相位,对附加相位进行Fourier滤波后计算大气多普勒.几何光学方法是在GPS 与 LEO 间单路径传播的假设下,利用多普勒公式、 Snell定律和掩星的几何关系,通过迭代方法计算弯曲角和碰撞参数(已知卫星的速度和位置)[11].
在局部球对称大气假设下,可通过Abel积分变换公式将弯曲角转化为折射指数,也可通过Abel积分将折射指数转化为弯曲角:
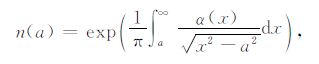
|
(1a) |
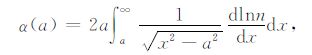
|
(1b) |
式中n为折射指数,α 为弯曲角,a为碰撞参数.在大气多路径条件下,同一碰撞参数会对应多个弯曲角的值,需对碰撞参数做单调化处理,才能做Abel积分变换.
通过弯曲角或折射率一维变分同化可以获得中性大气层的温度、压强以及湿度等大气参数[12];也可利用Smith-Weintraub 方程、理想气体方程和流体静力学方程直接从折射率得到大气参数(这时需要辅助的大气信息).
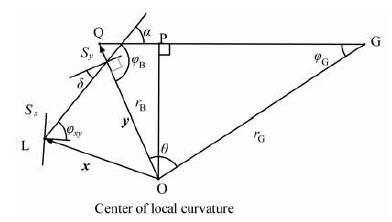
3 后向传播算法 3.1 掩星坐标系GPS和LEO 卫星历表的计算是在地心惯性坐标系中进行的,掩星点的位置一般在地固直角坐标系中表示,而弯曲角是在掩星坐标系中计算的.掩星坐标系如图 1 所示,图中O 为曲率中心,L 代表 LEO 卫星轨迹,G 代表GPS卫星.以GO 所在直线为x轴,正方向由G 点指向O 点.坐标原点定义为曲率中心,y轴与x轴垂直,正方向与LEO卫星在x轴的同一侧,且经过坐标原点.x轴、y轴以及曲率中心构成掩星坐标系.

|
图 1 掩星坐标系 Fig. 1 Occultation-plane coordinate |
在用后向传播方法进行反演之前,需对观测相位进行修正处理,使得GPS卫星在掩星坐标系中的位置固定[4].过G 作地球表面的切线,记切点为T,且要求切点与LEO 卫星在x轴的同侧.连接O 点与T 点,并延长至P 点,则OP 与GT 垂直.作一经过原点的线段OQ,OQ 所在直线即为辅助屏的位置,Q 和M 分别为辅助屏的上下端.记线段MQ 到 PT 的距离为d(点M 到直线OP 的距离约等于点 Q 到OP 的距离),由于OP 的位置固定不动,d的值即决定了辅助屏MQ 的位置,本文取113km 左右.
3.2 信号的后向传播后向传播方法的理论根据是真空中二维 Helmholtz方程的边值问题,边值条件是从沿LEO卫星轨道接收的复信号(即振幅与相位)得到.将二维Helmholtz方程通过Green函数展开,可以得到从辅助屏Sy到LEO 观测轨迹SL 上观测场的正向传播的电场解:
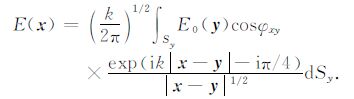
|
(2a) |
如果将观测得到的复信号E(x)从SL 向后传播到辅助屏Sy上,则得到辅助屏上的后向传播的电场解:
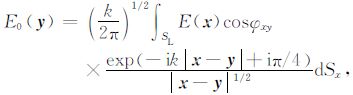
|
(2b) |
其中SL 是掩星过程中LEO 卫星运动的轨迹曲线(由于掩星时间很短,SL 可以近似为直线).辅助屏Sy取通过曲率中心的直线,k为波数,夹角φxy是矢量x-y与SL 的法向量nx的夹角(见图 2).通过公式(2b),可以将沿LEO 卫星轨迹的测量信号向后传播至辅助屏Sy.
公式(2a)~(2b)构成一组辅助屏与LEO 观测轨迹的信号场之间的变换.公式(2b)中指数部分与公式(2a)的互为相反数,代表不同的传播方向.公式(2b)中指数部分含有高速振荡性态,积分的主要贡献来自于驻相点附近的积分,可用驻相法求解.
3.3 计算弯曲角辅助屏Sy上的复信号E0(y)包含振幅和相位ΦE,需对其相位进行整周模糊度调整:
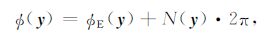
|
(3) |
其中N(y)为整周模糊度.得到后向传播场E0(y)的振幅和相位后,通过几何光学反演求解弯曲角和碰撞参数.矢量x-y与辅助屏法向量的夹角为[4]
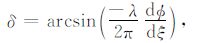
|
(4) |
其中ξ 为辅助屏上一点到曲率中心的距离.传播方向与矢量y之间的夹角为
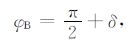
|
(5) |
通过Bouguer定律可得碰撞参数a与φG:
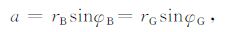
|
(6) |
其中rB= y为辅助屏上的点到曲率中心的距离,rG 为GPS到曲率中心的距离.弯曲角可通过几何关系得到:
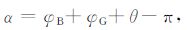
|
(7) |
其中θ 为矢量y与直线OG 之间的夹角.
在GPS/LEO 掩星数据处理中,将10km 以上利用几何光学方法计算的弯曲角,与10km 以下利用后向传播方法计算得到的弯曲角结合,组成一个新的弯曲角廓线,再由Abel积分变换反演得到大气折射指数廓线.
4 多相位屏模拟在几何光学近似下,可以采用射线追踪方法模拟掩星接收机获得的信号.但是在大气多路径条件下,射线追踪方法失效,利用多相位屏模型可以精确地模拟无线电复信号的传播过程[7].
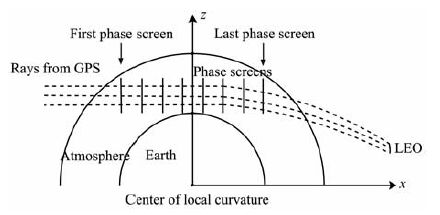
4.1 多相位屏基本原理图 3显示的是GPS卫星上的发射机发送信号,穿过地球大气,最后到达LEO 卫星的过程.信号从 GPS卫星到第一个相位屏的传播可用球面波的形式描述;在地球大气中的传播可用多相位屏近似;通过公式(2a),将最后一个相位屏上的复信号传播到 LEO 轨迹上.复信号穿过地球大气时,大气折射率的分布用一系列垂直于入射方向的相位屏替代,屏与屏之间假设为真空,大气的折射介质分布在相位屏内.当信号路径在折射介质内与直线的偏离小于大气折射率不规则性的最小尺度时,相位屏近似是合理的.
图 3中x轴代表无线电复信号的传播方向,z轴沿着相位屏的方向,原点为地球曲率中心.δx为屏与屏之间的距离,(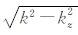
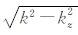
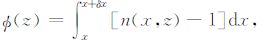
|
(8) |
其中n(x,z)为折射指数.
记未通过相位屏前的复信号是u(x,z),则通过相位屏后的复信号为
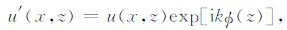
|
(9a) |
对u′(x,z)做Fourier变换,有:
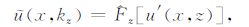
|
(9b) |
利用下面公式将u(x,kz)传播至下一个相位屏:
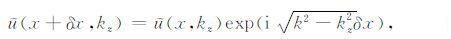
|
(9c) |
则x+δx处的复信号可通过Fourier逆变换得到:
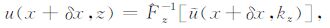
|
(9d) |
其中,$\hat{F}$z是关于z变量的Fourier 变换,$\hat{F}$z-1是Fourier逆变换.为加快计算速度,可用快速Fourier变换(FFT)进行计算.公式(9a)~(9d)实现了无线电复信号从一个相位屏传递到下一个相位屏的过程.重复过程(9a)~ (9d),可得到每个相位屏上的信号.
在本文的模拟中,取地球半径Re=6371km, 大气层高度hatm=130km.无线电波在大气中的传播总距离为
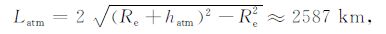
|
屏与屏之间的距离δx统一取为2km, 共约1300个相位屏.
4.2 利用多相位屏模拟大气多路径为了探讨低对流层的大气多路径效应对掩星资料反演的影响,利用EGOPS (End-to-End Generic Occultation Performance Simulation and Processing System)软件模拟信号.采用的大气折射率模型为[13, 14]
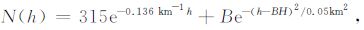
|
(10) |
其中h为距离地面的高度,公式(10)右边第二项决定大气多路径效应的强度和位置,常量B决定多路径的强度,BH决定多路径的位置.当B=0时,大气中不存在多路径效应;当B>0时,存在多路径效应,且随B的增大,多路径强度不断增加.
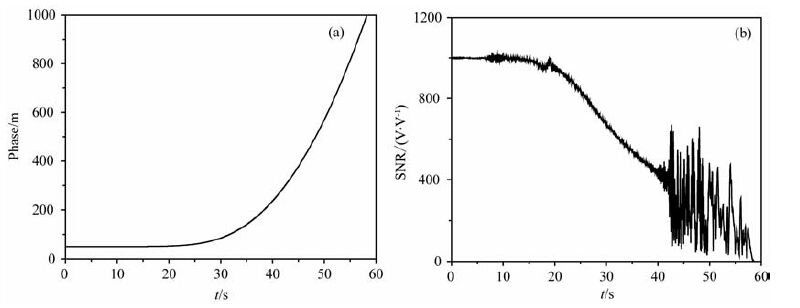
4.3 模拟结果采用多相位屏模型,数值模拟了强大气多路径条件下(强度B=10,BH=5km, 折射指数梯度的最大值为0.596×10-7m-1)无线电信号在大气中的传播过程,采样频率为50Hz.图 4显示的是模拟的相位和振幅,横坐标为掩星时间,图 4a纵坐标为相位,图 4b纵坐标为振幅.振幅在42s至56s有剧烈的振荡现象,为多路径发生区域.
|
图 4 相位和振幅(B=10) Fig. 4 Phase and amplitude(B=10) |
假设信号在接收过程中没有受到卫星的位置误差、接收机噪声与局部多路径等其他因素的影响,分别用几何光学方法和后向传播方法对模拟信号进行反演.
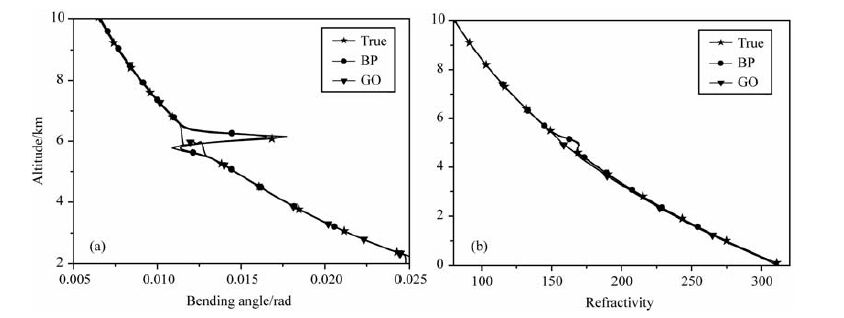
图 5a显示的是弯曲角反演结果,GO(下三角形)代表几何光学方法,BP(圆形)代表后向传播方法,True(星形)代表真值(由折射率廓线通过Abel积分得到),图 5b为相应的折射率廓线.在单路径区域,几何光学方法和后向传播方法都能准确地反演出大气参量廓线.在大气多路径区域,尤其在折射率梯度变化强烈的区域(如在大气边界层附近[15]),几何光学方法计算的弯曲角和折射率与真值有较大偏差,弯曲角出现多值情况.而后向传播方法计算的弯曲角和折射率与真值较为接近,且弯曲角不会出现多值情况.
|
图 5 弯曲角和折射率(B=10) Fig. 5 Bending angle and refractivity(B=10) |
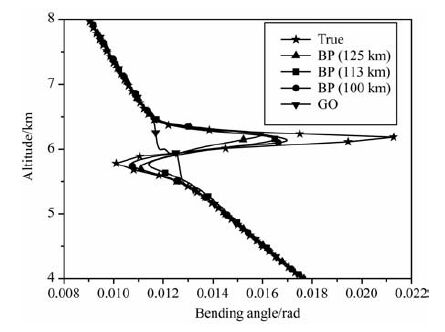
辅助屏的选择是后向传播方法的一个关键问题.辅助屏比LEO 观测轨迹更接近于地球大气,利用后向传播方法所得到的折射率具有更高的垂直分辨率.辅助屏的位置事先并不知道,不同多路径强度具有不同的最佳辅助屏位置.在多路径强度B≤10的情况下,d取77km~116km 都能取得较好的结果,且反演结果相差不大,取最佳位置为113km.当大气多路径强度进一步增大(B=15,折射指数梯度的最大值为0.788×10-7m-1),后向传播方法会偏离真值(见图 6).
|
图 6 弯曲角(B=15) Fig. 6 Bending angle(B=15) |
在图 6中,圆形、正方形和上三角形分别代表取d为100km、113km 和125km 时的后向传播方法.当d取113km 时,反演结果并不是最佳,辅助屏的最佳位置取为d=100km.一般地,多路径强度越大,辅助屏离直线OP 越近,即d的值越小.当多路径强度B=20 时,最佳位置难以找到,反演结果不理想,这时需要更好的全息反演方法.
5 CHAMP 掩星观测数据反演及误差统计由德国和美国联合研制的CHAMP 计划的主要任务包括重力、磁场、大气层和电离层等方面的研究,于2007年7 月发射升空,每天能提供大约200个CHAMP掩星廓线[16].本文采用的CHAMP 掩星数据是从COSMIC 网站(http://www.cosmic.ucar.edu/)下载的atmPhs资料.数据采集的时间为2007年第60天至第180天.
为了检验不同方法对实测资料的反演效果,分别用几何光学方法和后向传播方法对CHAMP 掩星数据进行反演.将其折射率反演结果与相应的 ECMWF分析场资料进行统计比较.比较区域按纬度分为:南半球(30°S~90°S)、热带(30°S~30°N)及北半球(30°N~90°N).数据插值所选取的步长为1km.
统计过程中,相对误差定义为
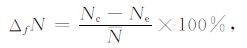
|
(11) |
其中,Nc 表示对CHAMP 掩星观测数据进行反演后得到的折射率;Ne 表示利用ECMWF 分析场资料计算的折射率;N 为Nc 与Ne 的平均值.
平均偏差计算公式如下:
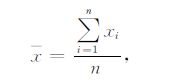
|
(12) |
均方差计算公式如下:

|
(13) |
其中,xi为第i个数据,n为数据维数.
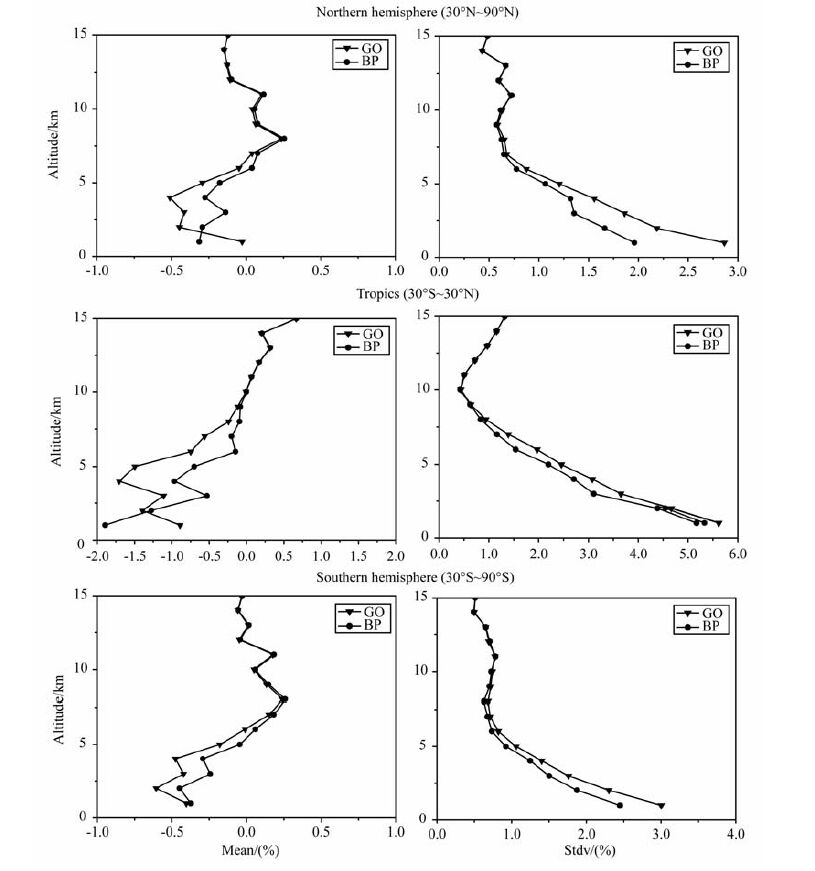
图 7 表示几何光学方法和后向传播方法反演 CHAMP 掩星观测数据得到的折射率与相应的 ECMWF 分析场资料之间的相对误差的平均偏差和均方差,从上往下依次为北半球(30°N~90°N)、热带(30°S~30°N)和南半球(30°S~90°S).从图 7可以看出:
|
图 7 折射率相对误差的平均偏差和均方差 Fig. 7 The average deviation and variance of fractional difference in refractivity |
(1) 在低对流层,后向传播方法反演折射率的相对误差的平均偏差和均方差普遍小于几何光学方法,说明后向传播方法反演精度高于几何光学方法.
(2) 从区域看,北半球(30°N~90°N)反演的精度是最好的,南半球(30°S~90°S)次之,热带(30S°~30°N)最差.这与低对流层中含有大量水汽有关[17~19].
(3) CHAMP掩星观测数据反演得到的折射率与ECMWF分析场资料相比,存在系统负偏差,而后向传播方法在一定程度上能减少这种负偏差.
6 结论在低对流层,尤其是在热带区域,经常发生大气多路径传播.例如在大气边界层,大气结构尺度小于菲涅耳直径,电磁波传播介质的梯度变化复杂,几何光学方法无法描述大气边界层的内部结构[20].基于真空中Helmholtz方程的后向传播方法将复原后的掩星复信号从接收机位置反推至更接近于地球大气的辅助屏.通过减小地球大气与辅助屏的距离,使得大气多路径效应的影响减少.
采用多相位屏的数学模型对大气多路径条件下的无线电信号的传播过程进行了数值模拟,分别用几何光学方法和后向传播方法反演弯曲角,并与真值进行比较,结果验证了后向传播方法的可行性与准确性.模拟结果同时表明:(1)在大气单路径条件下,几何光学方法和后向传播方法都能反演得到准确的大气参数;(2)在大气多路径条件下,后向传播方法消弱了多路径效应的影响,其反演结果比几何光学方法更精确.但后向传播方法依然无法完全消除多路径效应的影响,当低对流层中含较大的折射率梯度或超折射时,后向传播方法将可能失效.且后向传播方法反演的精度依赖于辅助屏的选择.
分别用几何光学方法和后向传播方法对2007年第60天至180天约15000个CHAMP 掩星观测数据进行反演,将其折射率反演结果与ECMWF 分析场资料进行统计比较,结果表明:在低对流层,后向传播方法反演折射率的相对误差的平均偏差和均方差普遍小于几何光学方法.后向传播方法具有更高的垂直分辨率,能提供对流层(尤其是低对流层)更详细的信息,从而为数值天气预报提供便利.
致谢对奥地利Graz大学的地球物理、天体物理和气象研究所提供EGOPS 软件和COSMIC Data Analysis and Archive Center(CDAAC)提供CHAMP掩星观测资料表示感谢.
| [1] | Anthes R A, Bernhardt P A, Chen Y, et al. The COSMIC/FORMOSAT-3 mission: Early results. Bull. Am. Meteorol. Soc. , 2008, 89(3): 313-333. DOI:10.1175/BAMS-89-3-313 |
| [2] | 胡雄, 曾桢, 张训械, 等. 大气GPS掩星观测反演方法. 地球物理学报 , 2005, 48(4): 768–774. Hu X, Zeng Z, Zhang X X, et al. Atmospheric inversion methods of GPS radio occultation. Chinese J. Geophys. (in Chinese) , 2005, 48(4): 768-774. |
| [3] | 徐贤胜, 洪振杰, 郭鹏, 等. COSMIC掩星电离层资料反演以及结果验证. 物理学报 , 2010, 59(3): 2163–2168. Xu X S, Hong Z J, Guo P, et al. Retrieval and validation of ionospheric measurements from COSMIC radio occultation. Acta Phys. Sin. (in Chinese) , 2010, 59(3): 2163-2168. |
| [4] | Kursinski E R, Hajj G A, Leroy S S, et al. The GPS radio occultation technique. Terr. Atmos. Ocean. Sci. , 2000, 11(1): 53-114. |
| [5] | Gorbunov M E, Gurvich A S. Microlab-1 experiment: Multipath effects in the lower troposphere. J. Geophys. Res. , 1998, 103(D12): 13819-13826. DOI:10.1029/98JD00806 |
| [6] | Sokolovskiy S V. Modeling and inverting radio occultation signals in the moist troposphere. Radio Sci. , 2001, 36(3): 441-458. DOI:10.1029/1999RS002273 |
| [7] | Gorbunov M E. Canonical transform method for processing radio occultation data in the lower troposphere. Radio Sci. , 2002, 37(5): 1076. DOI:10.1029/2000RS002592 |
| [8] | Jensen A S, Lohmann M S, Benzon H H, et al. Full spectrum inversion of radio occultation signals. Radio Sci. , 2003, 38(3): 1040. DOI:10.1029/2002RS002763 |
| [9] | Marouf E A, Tyler G L, Rosen P A. Profiling Saturn's rings by radio occultation. Icarus , 1986, 68(1): 120-166. DOI:10.1016/0019-1035(86)90078-3 |
| [10] | Karayel E T, Hinson D P. Sub-Fresnal-scale vertical resolution in atmospheric profiles from radio occultation. Radio Sci. , 1997, 32(2): 411-423. DOI:10.1029/96RS03212 |
| [11] | 郭鹏, 严豪健, 洪振杰, 等. 中性大气掩星标准反演技术. 天文学报 , 2005, 46(1): 96–107. Guo P, Yan H J, Hong Z J, et al. The standard retrieval algorithm of neutral atmosphere by GPS occultation. Acta Astron. Sin. (in Chinese) , 2005, 46(1): 96-107. |
| [12] | 洪振杰, 郭鹏, 刘敏, 等. GPS掩星折射率剖面一维变分同化. 天文学报 , 2006, 47(1): 100–110. Hong Z J, Guo P, Liu M, et al. 1DVAR retrieval of refractivity profiles by GPS occultation. Acta Astron. Sin. (in Chinese) , 2006, 47(1): 100-110. |
| [13] | Benzon H H, Nielsen A S, Olsen L. An atmospheric wave optics propagator-Theory and application. Scientific Report 03-01. Copenhagen, Denmark: Danish Meteorological Institute, 2003 . |
| [14] | Kirchengast G, Schweitzer S, Ramsauer J, et al. End-to-end GNSS occultation performance simulator version 5 (EGOPSv52) software user manual. Report ESA/ESTEC No. 4/2007. Graz, Austria: University of Graz, 2007 . |
| [15] | Sokolovskiy S, Kuo Y H, Rocken C, et al. Monitoring the atmospheric boundary layer by GPS radio occultation signals recorded in open-loop mode. Geophys. Res. Lett. , 2006, 33. DOI:10.1029/2006GL025955 |
| [16] | Wickert J, Reigber C, Beyerle G, et al. Atmosphere sounding by GPS radio occultation: First results from CHAMP. Geophys. Res. Lett. , 2001, 28(17): 3263-3266. DOI:10.1029/2001GL013117 |
| [17] | Ao C O, Meehan T K, Hajj G A, et al. Lower troposphere refractivity bias in GPS occultation retrievals. J. Geophys. Res. , 2003, 108: 4577. DOI:10.1029/2002JD003216 |
| [18] | Beyerle G, Gorbunov M E, Ao C O. Simulation studies of GPS radio occultation measurements. Radio Sci. , 2003, 38(5): 1084. DOI:10.1029/2002RS002800 |
| [19] | 王鑫, 吕达仁. GPS无线电掩星技术反演大气参数方法对比. 地球物理学报 , 2007, 50(2): 346–353. Wang X, Lü D R. Comparative analysis of inversion methods of retrieving atmospheric profiles with GPS occultation measurements. Chinese J. Geophys. (in Chinese) , 2007, 50(2): 346-353. |
| [20] | Guo P, Kuo Y H, Sokolovskiy S V, et al. Estimating atmospheric boundary layer depth using COSMIC radio occultation data. J. Atmos. Sci. , 2011, 68: 1703-1713. DOI:10.1175/2011JAS3612.1 |
 2011, Vol. 54
2011, Vol. 54