2. 中国石油大学(北京)油气资源与探测国家重点实验室,北京 102249;
3. 中国石油新疆油田分公司,新疆 克拉玛依 843000
2. State Key Laboratory of Petroleum Resource and Prospecting, China University of Petroleum, Beijing 102249, China;
3. CNPC Xinjiang Oilfield Branch, Xinjiang Karamay 843000, China
自然电位测井测量的是由地层原生水、钻井液和具有离子交换的泥岩之间共同作用产生的电化学电位.利用自然电位测井曲线可以划分渗透层,求取地层水电阻率等.研究自然电位测井的响应特征及影响因素是其应用好坏的关键,通过大量文献资料的调研,国内外对影响自然电位的因素的研究主要体现在:(1)地层水和泥浆滤液中的含盐浓度比值[1~3];(2)岩性的影响[4, 5];(3)地层厚度的影响[6~8];(4)含油气的影响[9~11];(5)井径扩大和泥浆侵入的影响[12].对于以欠压实作用为主要成因的超压地层,压实作用是否对自然电位造成影响,进而影响超压泥质砂岩储层的自然电位响应特征,相关研究未见文献报道,而且该项研究对利用自然电位曲线识别欠压实超压储层具有参考价值,因此有必要开展欠压实超压层自然电位测井响应机理的研究.
本文主要以欠压实超压层为研究对象,受到 Clavier提出“理想泥岩"概念的启发,利用双水模型和热动力学理论,推导欠压实超压泥质砂岩、泥岩的薄膜电位方程,并依据推导方程,分析压实作用对薄膜电位造成的影响,最后分析欠压实超压泥质砂岩储层自然电位的响应特征.
2 欠压实超压泥岩、泥质砂岩薄膜电位方程推导 2.1 理想泥岩与欠压实超压泥岩Clavier等的文章在提出双水模型的同时也引入了“理想泥岩"的概念[13].
双水模型把泥质砂岩岩石中的水分为两部分,一部分是由偶电层引起的粘土水(又称近水),粘土水不含盐但含所有的平衡阳离子.粘土水的电导率与粘土类型及平衡阳离子的浓度均无关,而只与温度有关.Clavier等相信,粘土水通常比岩石中的体积水要淡.另一部分水是远离粘土的水(又称远水),其导电性质与岩石中的体积水相同.两部分水构成了岩石的并联导电通道.
双水模型的提出不仅为引入“理想泥岩"的概念提供了理论基础,更为理解欠压实超压泥岩层提供了有效的途径.根据扩散双电层理论和双水模型,盐水中两个粘土颗粒之间是平行的,间距大于或等于20Å.之间包括两个扩散层的粘土水(12.3Å)和远离粘土的水(7.7Å).在正常压实的泥岩层中,远水因为上覆压力的作用而被挤出,当所有的远水被挤出时,泥岩层就是一种理想的状态.在不均衡压实作用形成的超压泥岩层中,因为在快速沉积过程中,上覆负荷急剧增加,孔隙容积趋向于快速减小,流体的排出速度无法平衡孔隙容积的减少,于是部分流体将滞留于孔隙中.即在超压泥岩层中,包含有大量的“远水".
2.2 饱含水的欠压实超压泥质砂岩电导率方程设欠压实超压地层的孔隙度为Φ,正常压实地层的孔隙度为Φt, 由于在欠压实引起的超压层中,欠压实超压地层的孔隙度Φ 要大于正常压实地层的孔隙度Φt, 多出的体积被滞留于孔隙中的自由流体占据,故欠压实超压层中自由水(远水)的孔隙体积为
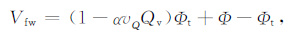
|
(1) |
其中,当远水溶液浓度〈n〉大于某一数值〈n1〉时,α=1,当远水溶液浓度〈n〉小于〈n1〉时,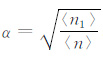
欠压实超压层中粘土水的孔隙体积表达式与正常压实地层一样为
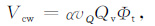
|
(2) |
因此欠压实超压层中单位孔隙粘土水的体积百分比为
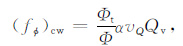
|
(3) |
欠压实超压层中单位孔隙自由水的体积百分比为
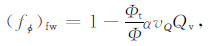
|
(4) |
正常压实地层的孔隙度Φt 与欠压实地层的孔隙度Φ 的比值为
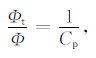
|
(5) |
其中,Cp为压实系数,可以通过声波测井资料确定.
由此,欠压实超压层中单位孔隙粘土水产生的电导为
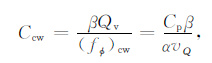
|
(6) |
其中,β 为平衡阳离子等效电导,在25 ℃ 时,等于2.05mL/(Ωm·meq).
欠压实超压层中单位孔隙自由水产生的电导为
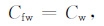
|
(7) |
其中,Cw 为自由水(远水)的电导率.
由于自由水和补偿钠离子对岩石导电的贡献跟岩石的孔隙度和曲折度有关,换言之,地层水的有效电导率Cwe 为
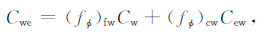
|
(8) |
或者用式(9)表示:
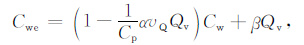
|
(9) |
即可推导出饱含水的欠压实超压泥质砂岩电导率方程:
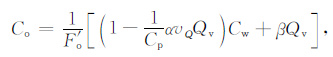
|
(10) |
其中,F′o为地层因素,区别于双水模型中的Fo.
2.3 欠压实超压泥质砂岩薄膜电位方程当含有两种不同浓度的溶液在泥质砂岩中相互接触时,可以将泥质砂岩看成具有大量孔隙的渗透性薄膜,泥质砂岩中可迁移的离子包括两部分:一部分为平衡离子,另一部分为自由电解液.由于平衡离子引起的正负离子迁移数的改变,使得两种不同浓度的盐溶液相互接触时,可以产生与纯砂岩不同的特性.
根据式(10),补偿钠离子和自由水对岩石导电的贡献分别由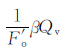
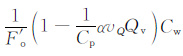
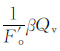
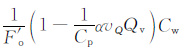
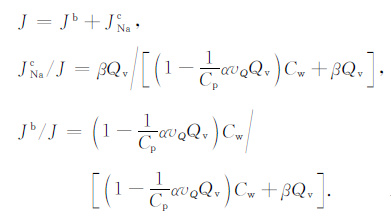
|
(11) |
同理,钠离子携带的电流也可以分成两部分,即JNa =JNab +JNac;钠离子的迁移数可以定义为所有钠离子携带的电流与总电流的比,tNa =JNa/J;自由水钠离子的迁移数可以定义为tNab =JNab/Jb.结合式(11)可以得到钠离子的迁移数为
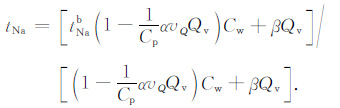
|
(12) |
式(12)可以看出,不包含地层因素F′o, 扩散电位的大小不依赖于孔隙的曲折程度.根据StavermanA J公开发表的文献[14]可知,自由水钠离子的迁移数近似等于自由溶液的Hittorf迁移数,即
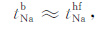
|
(13) |
把式(13)代入式(12)可得
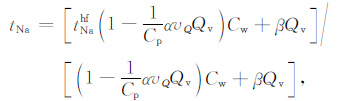
|
(14) |
因此,归一化的钠离子的迁移数为
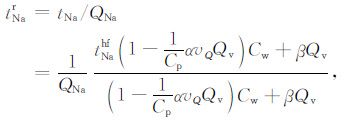
|
(15) |
其中,QNa 为可交换的钠离子迁移容量.
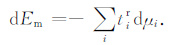
|
(16) |
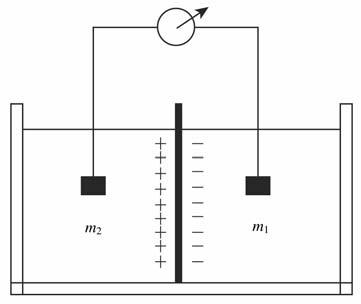
由于电极电位的存在,实验室测量的电动势并非是真正的扩散电动势或者薄膜电动势.只有当可逆电极与溶液接触时,实验测量的电动势可用热动力校正的方式得到扩散电动势或者薄膜电动势.对于氯化钠溶液,可以应用Ag-AgCl电极,电化学电瓶装置可以用图 1描述.
|
图 1 电化学电瓶装置示意图 Fig. 1 The sketch map of electrochemistry cell apparatus |
根据式(16),得到薄膜电位的表达式为
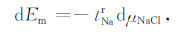
|
(17) |
式(15)代入式(17),可得
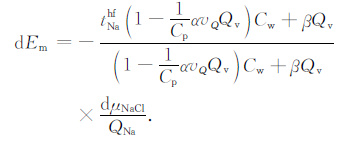
|
(18) |
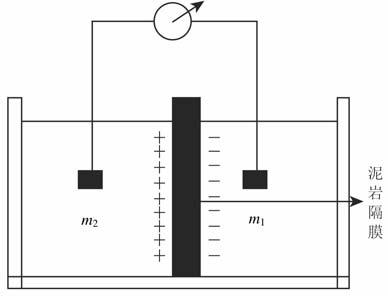
同样,扩散电位的电瓶装置可以用图 2描述.
|
图 2 扩散电位的电瓶装置示意图 Fig. 2 The sketch map of diffusion potential cell apparatus |
根据式(16),得到扩散电位的表达式为
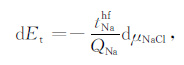
|
(19) |
式(19)代入式(18),可得
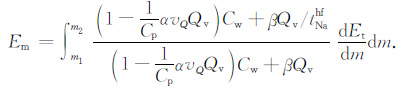
|
(20) |
电解质离子的平均活度与扩散电位Et的关系为
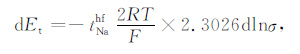
|
(21) |
其中,R为克分子气体常数,等于8.314J/(mol·K);T为绝对温度,K;F为Farady常数,等于96500C/mol;σ 为平均活度.
式(21)代入式(20),可得薄膜电位的表达式为
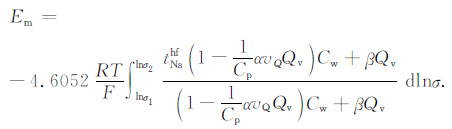
|
(22) |
利用式(22)可以研究压实作用对薄膜电位的影响,进而研究欠压实超压泥岩、泥质砂岩薄膜电位的响应规律.
由于式(22)是一个积分解,对其参数物理意义的理解和参数值的确定是成功应用该公式的关键.其中,Cw 为自由水的电导率,这里取两种等效氯化钠溶液的平均值;当这两种等效氯化钠溶液的平均浓度〈m〉大于0.35mol/L 时,α=1,当这两种等效氯化钠溶液的平均浓度〈m〉小于0.35 mol/L 时,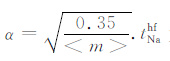
|
|
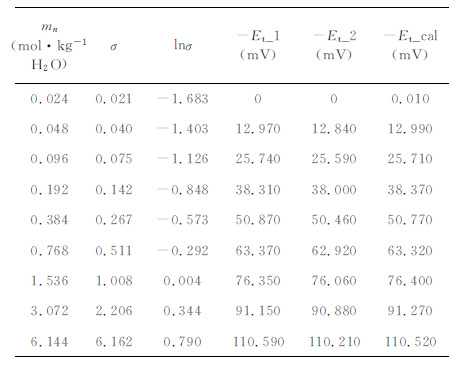
表 1 不同浓度的NaCl溶液测量的电池扩散电位(-Et, 25 ℃)[16] Table 1 Diffusion potential measured using different concentration solution[16] |
根据表 1中的数据,扩散电位-Et 与电解质离子的平均活度具有很好的相关关系,相关公式如下:
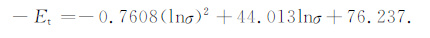
|
(23) |
将式(23)代入式(21),可以得出自由溶液的 Hittorf迁移数tNahf 与电解质离子的平均活度的关系式如下:
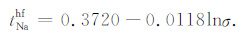
|
(24) |
因此,在设定两种氯化钠溶液的浓度以及阳离子交换量Qv 之后,将式(24)代入式(22),就可以得到不同压实系数下薄膜电位Em 与阳离子交换量Qv之间的关系.
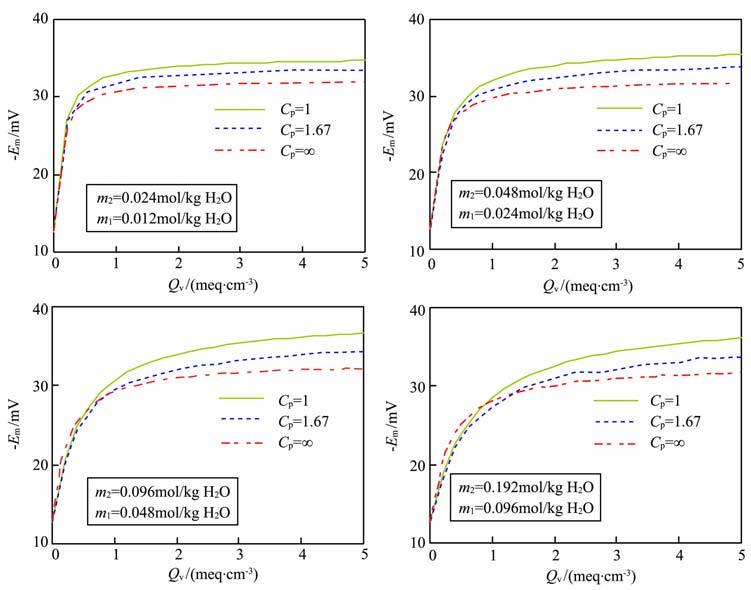
为了研究压实作用对薄膜电位的影响,模拟计算了4对不同泥浆滤液/地层水浓度下,不同压实系数、不同阳离子交换量的薄膜电位,如图 3.通过图 3可以得出如下认识:
|
图 3 压实作用对薄膜电位的影响 Fig. 3 The effect of membrane potential by compaction |
(1) 泥岩薄膜电位受压实作用的影响大,对于盐水泥浆(Rmf<Rw),泥岩薄膜电位随压实系数的变大而增大,对于淡水泥浆(Rmf>Rw),泥岩薄膜电位随压实系数的变大而减小,同时压实作用对阳离子交换容量较小的泥质砂岩的影响较小;
(2) 对于泥质砂岩,阳离子交换容量对薄膜电位的影响远大于压实作用.
4 欠压实超压储层自然电位响应特征根据自然电位原理和W-S模型,Smits提出了等效氯化钠溶液的自然电位SP物理模型[17~20]
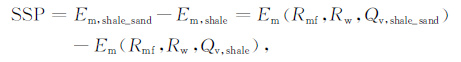
|
(25) |
其中,SSP 为静自然电位(自然电位异常幅度),mV;Em, shale_sand 为泥质砂岩薄膜电位,mV;Em, shale 为泥岩薄膜电位,mV;Rmf、Rw 分别为泥浆滤液电阻率和地层水电阻率,Ωm;Qv, shale_sand、Qv, shale 分别为泥质砂岩阳离子交换容量和泥岩阳离子交换容量,meq/cm3.
由于式(25)是针对正常压实地层推导出来的,不适合用于欠压实超压泥质砂岩,因此,在考虑压实作用的情况下,可以将式(25)改为
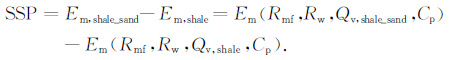
|
(26) |
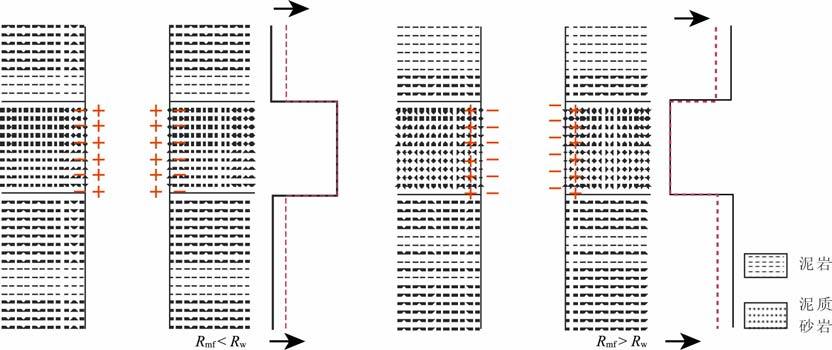
由式(26)和压实作用对薄膜电位的影响分析可知:欠压实作用会使得泥岩的自然电位基线发生偏移,导致欠压实超压泥质砂岩自然电位异常幅度 SSP较正常压实泥质砂岩低.图 4 为欠压实线(虚线)与正常压实线(实线)的线型示意图,从图中可以看出,当钻井选用淡水泥浆时(Rmf>Rw),欠压实超压泥岩的SP基线值变小,而泥质砂岩变化不大,导致泥质砂岩段自然电位的幅度值降低;当钻井选用盐水泥浆时(Rmf<Rw),欠压实超压泥岩的SP 基线值变大,而泥质砂岩变化很小,同样地导致泥质砂岩段自然电位的幅度值降低.
|
图 4 欠压实线与正常压实线的线型说明 Fig. 4 Linear description of undercompaction line and normal compaction line |
通过对欠压实超压层自然电位响应机理研究,可以得出以下结论:
(1) 泥岩薄膜电位受压实作用的影响大,对于盐水泥浆(Rmf<Rw),泥岩薄膜电位随压实系数的变大而增大,对于淡水泥浆(Rmf>Rw),泥岩薄膜电位随压实系数的变大而减小;
(2) 压实作用对阳离子交换容量较小的泥质砂岩的影响较小;
(3) 对于泥质砂岩,阳离子交换容量对薄膜电位的影响远大于压实作用;
(4) 欠压实作用会使得泥岩的自然电位基线发生偏移,导致欠压实超压泥质砂岩自然电位异常幅度SSP较正常压实泥质砂岩低.
| [1] | 欧阳健, 毛志强, 修立军, 等. 测井低对比度油层成因机理与评价方法. 北京: 石油工业出版社, 2009 . Ouyang J, Mao Z Q, Xiu L J, et al. Log Low Contrast Reservoir Genetic Mechanism and Evaluation Method (in Chinese). Beijing: Petroleum Industry Press, 2009 . |
| [2] | 中国石油勘探与生产公司. 低阻油气藏测井识别评价方法与技术. 北京: 石油工业出版社, 2006 . Petrochina E & P Company. Low Resistivity Oil/ Gas Reservoirs Log Identification Method and Technology (in Chinese). Beijing: Petroleum Industry Press, 2006 . |
| [3] | 杨瑞明, 王良书, 徐正顺, 等. 大庆油田高含水期自然电位的变异和校正. 石油勘探与开发 , 2003, 30(1): 60–61. Yang R M, Wang L S, Xu Z S, et al. The distortion and correction of SP logs of reservoirs at high water-cut stage in Daqing oil field. Petroleum Exploration and Development (in Chinese) , 2003, 30(1): 60-61. |
| [4] | 房文静, 关继腾. 利用毛管模型研究泥岩自然电位特性. 石油大学学报(自然科学版) , 2001, 25(4): 97–102. Fang W J, Guang J T. Study on prosperity of shale spontaneous potential by capillary model. Journal of the University of Petroleum, China (Edition of National Science) (in Chinese) , 2001, 25(4): 97-102. |
| [5] | 付晨东, 王伟男, 曹雅芳. 松辽盆地北部深层火成岩储层自然电位形成机理. 测井技术 , 2006, 30(5): 397–399. Fu C D, Wang W N, Cao Y F. Mechanism of forming spontaneous potential in deep igneous rock reservoir of northern Songliao basin. Well Logging Technology (in Chinese) , 2006, 30(5): 397-399. |
| [6] | 张庚骥. 电法测井. 东营: 石油大学出版社, 1996 . Zhang G J. Electrical Method Logging (in Chinese). Dongying: University of Petroleum Press, 1996 . |
| [7] | 姜恩承, 王敬农, 孙宝佃, 等. 电化学测井理论研究及其应用的新进展(上). 测井技术 , 1999, 23(4): 258–263. Jiang E C, Wang J N, Sun B D, et al. New advances in theoretical study and practical application of electrochemical logging. Well Logging Technology (in Chinese) , 1999, 23(4): 258-263. |
| [8] | 袁宁, 聂小春, 聂在平. 自然电位测井的定量分析与应用研究. 测井技术 , 1999, 23(1): 9–14. Yuan N, Nie X C, Nie Z P. Quantitative analysis and application of spontaneous potential log. Well Logging Technology (in Chinese) , 1999, 23(1): 9-14. |
| [9] | 邓少贵, 范宜仁. 含油气泥质砂岩薄膜电位理论及其在测井中的应用. 石油大学学报(自然科学版) , 2004, 28(5): 34–37. Deng S G, Fan Y R. Membrane potential of oil and gas-bearing shaly sand and its application in petrophysics. Journal of the University of Petroleum, China (Edition of National Science) (in Chinese) , 2004, 28(5): 34-37. |
| [10] | 周凤鸣, 程相志, 周灿灿. 泥质砂岩薄膜电位与含油性的关系及其在测井中的应用. 测井技术 , 2005, 29(4): 302–304. Zhou F M, Cheng X Z, Zhou C C. The relationship between membrane potential and hydrocarbon saturation of the shaly sands and its application in well logging. Well Logging Technology (in Chinese) , 2005, 29(4): 302-304. |
| [11] | 黄导武, 刘建新. 海上油气田油气水层自然电位特征及机理浅析. 测井技术 , 2006, 30(2): 164–167. Huang D W, Liu J X. Analysis of the offshore oil or gas reservoirs'spontaneous potential characteristic and its orgin. Well Logging Technology (in Chinese) , 2006, 30(2): 164-167. |
| [12] | 王斌, 范晓敏, 陈启艳, 等. 用有限差分法模拟自然电位测井的侵入带影响. 测井技术 , 2008, 32(2): 164–168. Wang B, Fan X M, Chen Q Y, et al. Modeling effect of invaded zone on SP log with finite difference method. Well Logging Technology (in Chinese) , 2008, 32(2): 164-168. |
| [13] | Clavier C, Coates G, Dumanoir J. Theory and experimental basis for the dual-water model for interpretation of shaly sands. SPE Formation Evaluation , 1977, 13(2): 25-37. |
| [14] | Staverman A J. Non-equilibrium thermodynamics of membrane processes. Trans. Faraday Soc. , 1952, 48(2): 176-185. |
| [15] | Wyllie M R J. A quantitative analysis of the electrochemical component of the SP curve. Trans.AIME , 1949, 186: 17-26. |
| [16] | Smits L J M, Duyvis E M. Transport numbers of concentrated sodium chloride solutions at 25℃. Journal of Physics and Chemistry , 1966, 70(2): 2743-2747. |
| [17] | Smits L J M. SP log interpretation in shaly sands. Society of Petroleum Engineers Journal , 1968, 2(4): 123-136. |
| [18] | Hill H J, Winsauer J D. Effect of clay and water salinity on electrochemical behaviour of reservoir rock. AIME , 1956, 207(1): 65-72. |
| [19] | Waxman M H, Smits L J M. Ionic double-layer conductivity in oil-bearing shaly sands. SPE Formation Evaluation , 1968, 4(1): 20-32. |
| [20] | Waxman M H. Electrical conductivities in shaly sands: (I) the relation between hydrocarbon saturation and resistivity index; (II) the temperature coefficient of electrical conductivity. Journal of Petroleum Technology , 1974, 26(3): 213-225. |
 2011, Vol. 54
2011, Vol. 54