2. 北方工业大学理学院,北京 100144
2. College of Sciences, North China University of Technology, Beijing 100144, China
中国国土资源航空物探遥感中心2007 年成功引进并集成了国内资源勘查领域首套能够满足中小比例尺区域重力勘探精度要求的GT-1A 航空重力勘查系统[1, 2].由于航空重力是在高速运动的飞机载体上进行测量的,因此飞机的高频振动将不可避免对重力仪测量数据产生高频干扰影响.这种高频随机干扰的频率和强度通常比由地球密度和结构变化引起的重力加速度信号即重力异常的频率和强度高得多.为尽可能消除或减弱这种高频强干扰影响,提取出有意义的低频和弱强度的重力异常信号,GT-1A 系统采用FIR(Finite Impulse Response)和卡尔曼(Kalman)滤波等技术进行低通数字滤波处理[3~15].为探究其滤波方法原理和技术,我们对窗函数FIR 低通数字滤波方法进行过试验研究并获得较好效果[3].本文采用巴特沃思和切比雪夫逼近,设计IIR 低通数字滤波器,对GT-1A 系统获得的测量数据进行了滤波试验研究.
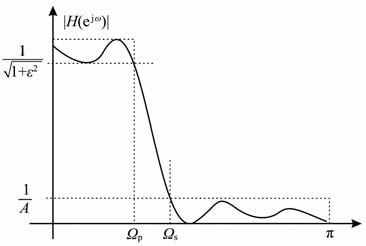
2 IIR 低通滤波方法 2.1 IIR低通滤波IIR 低通滤波器可借助常见的经典模拟低通滤波器的方法加以实现[6, 7].模拟低通滤波器的设计中,一般给定通带上限截止频率Ωp、阻带下限截止频率Ωs、通带允许的最大衰减αp、阻带允许的最小衰减αs(图 1).为了规范设计,通常将频率用通带截止频率Ωp 进行归一化,采用相对频率λ=Ω/Ωp, 此时的滤波器成为标准滤波器形式.
|
图 1 低通滤波器的绝对技术指标示意图 Fig. 1 Sketch map of absolute technical parameters of lowpass filter |
对于经典滤波器,其设计关键是用归一化频率λ 的多项式或多项式之比来逼近滤波器的幅值平方函数H(λ)2.n阶低通滤波器的幅值平方函数和衰减方程分别为

|
(1) |
式中ε是待定参数,Ln(λ)是一个与幅值平方函数相关的n阶多项式或有理函数.
根据设计指标和方程(1),可得滤波器衰减指标与幅值平方函数的关系式:
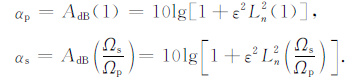
|
(2) |
通过对滤波器衰减关系式的计算,可以求得滤波器的待定参数ε和多项式阶数n,从而建立滤波器响应函数(或称传递函数)的准确表达式.比较常用的模拟低通滤波器有巴特沃思逼近、切比雪夫逼近等方式.
2.2 巴特沃思逼近巴特沃思逼近的低通滤波器选用巴特沃思多项式[6, 7]:Ln(λ)=λn.
则有:
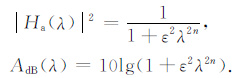
|
根据通带上限截止频率Ωp、阻带下限截止频率Ωs、通带允许的最大衰减αp、阻带允许的最小衰减αs 可确定幅值平方函数中的待定参数ε和滤波器阶数n:

|
(3) |
令λ2 =-s2,并且只取复平面左半平面的极点:
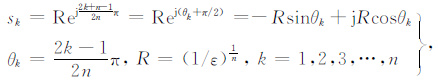
|
(4) |
则归一化Butterworth低通滤波器的传递函数:
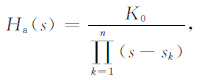
|
(5) |
其中归一化常数K0 可由传递函数代入s= 0,Ha(0)=1计算获得.
2.3 切比雪夫逼近
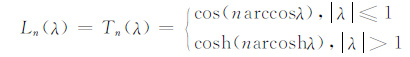
|
则有:
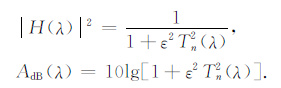
|
滤波器待定参数ε、滤波器阶数n可由通带最大衰减、阻带最小衰减求得:
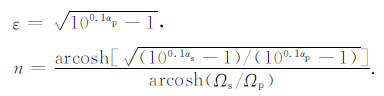
|
(6) |
令λ2 =-s2,则s=jcosφ,φ =arccos(s/j)=φ1 + jφ2,考虑左半平面的极点:
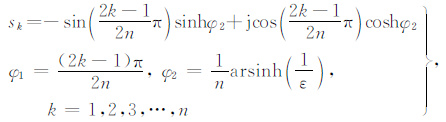
|
(7) |
则归一化Chebyshev低通滤波器的传递函数:
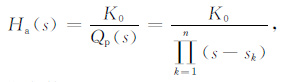
|
(8) |
其中归一化常数:
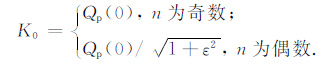
|
通常可采用双线性变换法、脉冲响应不变法等方法通过模拟滤波器来设计IIR 低通数字滤波器,下面简单叙述由双线性变换法设计IIR 低通数字滤波器的步骤[6, 13]:
(1) 将给定的数字滤波器的设计指标变换为模拟滤波器的设计指标.
利用双线性变换的频率变换式将给定的数字滤波器的ωp、ωs 转换为
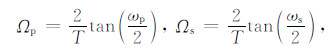
|
αp、αs 参数不变.为方便计算,可假设采样间隔T=1.
(2) 设计低通模拟滤波器的传递函数Ha(s).
如果选定巴特沃思逼近或切比雪夫逼近,则可由式(5)或式(8)获得相应低通滤波器的传递函数Ha(s).对于实际滤波器,传递函数中的s应该替换为归一化相对频率s/Ωp, 则有:
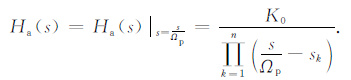
|
(3) 将Ha(s)转换为数字滤波器的传递函数H(z).
利用双线性变换映射公式: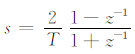
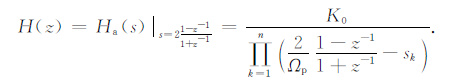
|
(4) 将H(z)转换为数字滤波器的频率响应H(ejω).
令z=ejω 代入H(z)可得数字滤波器的频率响应H(ejω)[6, 13]:
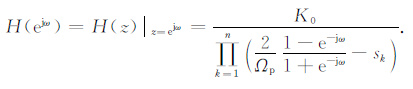
|
(9) |
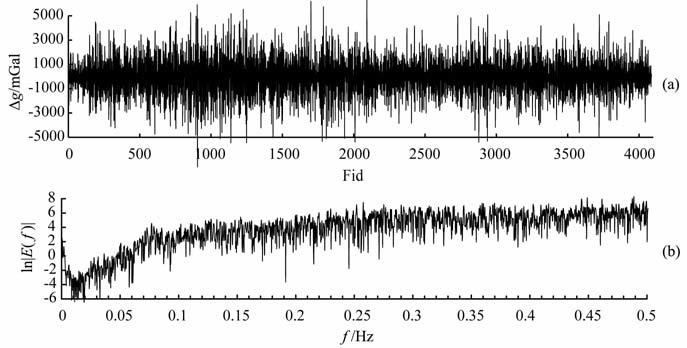
图 2为GT-1A 系统3010线原始未滤波航空自由空间重力异常[3]及其归一化对数功率谱,集中在小于0.02Hz低频段的有用的重力异常信号完全淹没在高频噪声干扰中,噪声幅度大致在±5000mGal的范围内变化.图 2a横轴Fid为测线基准点号,间距平均为30m;图 2b横轴f为以Hz为单位的频率.根据巴特沃思、切比雪夫逼近的IIR 低通滤波方法及式(1)~式(9),我们研制了相应数字滤波器的软件,对图 2的原始未滤波数据分别进行了截止波长100s、60s长度(按v=60 m/s的航速计算,截止波长λc 分别为6km、3.6km, 按fc=v/λc 计算的截止频率分别为0.01 Hz、0.0167 Hz)的巴特沃思和切比雪夫IIR 低通滤波试验计算,所采用的低通数字滤波器的设计参数值见表 1、幅频响应见图 3.表 1中选择的滤波器截止波长主要依据是与GT-1A 系统100s和60s的滤波时间长度相对应,通带、阻带衰减和滤波器阶数等参数则根据试验对比效果确定.从图 3中看到,切比雪夫比巴特沃思IIR 滤波器幅频响应曲线在截止频率处的过渡带更陡峭,但以其通带波纹为代价.考虑到IIR滤波器的相位非线性特点,实际使用时我们只选用其幅频响应函数进行低通滤波计算,获得的滤波结果见图 4~ 图 7(蓝色曲线),图中GT-1A 系统100s、60s滤波航空自由空间重力异常测线数据(红色曲线)是采用GT-1A 系统配套的数据处理软件获得的滤波结果[14, 15],滤波后高频干扰已基本消除,而幅度通常只有百十毫伽的由密度和构造变化等地质因素引起的重力异常则较好地显现出来.为了图形对比方便,各剖面图中仍然保留了测线边部两端的各半个滤波窗口数据,这些数据由于存在边部效应,因而是不准确的,实际应用时应该去掉.
|
图 2 GT-1A系统原始未滤波航空自由空间重力异常(a)及归一化对数功率谱(b) Fig. 2 GT-1Araw unSiltered airbornegravity freeair anomaly (a) and its unitary logarithm energy spectrum (b) |
|
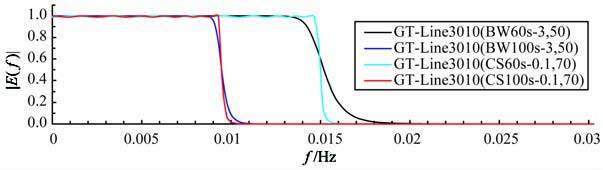
图 3 截止波长100 s、0 s巴特沃思和切比雪夫IIR数字低通滤波器幅频响应 Fig. 3 Amplitude response of Butterworth and Chebyshev IIR digital lowpass filter with cutoff wavelength 100 s and 60 s |
|
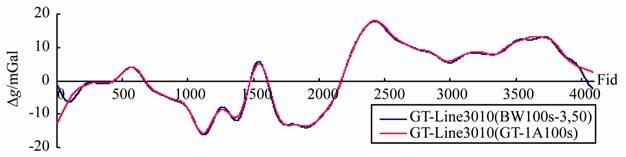
图 4 巴特沃思滤波器与GT-1A系统100 s滤波航空自由空间重力异常对比图 Fig. 4 Airborne gravity free air anomaly of Butterworth and GT-1A 100 s filter |
|
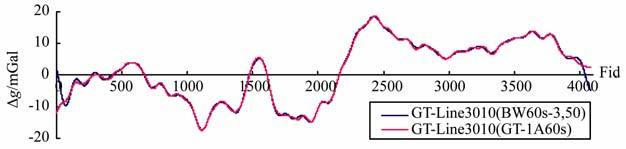
图 5 巴特沃思滤波器与GT-1A系统60 s滤波航空自由空间重力异常对比图 Fig. 5 Airborne gravity free air anomaly of Butterworth and GT-1A 60 s filter |

|
图 6 切比雪夫滤波器与GT-1A系统100 s滤波航空自由空间重力异常对比图 Fig. 6 Airborne gravity free air anomaly of Chebyshev and GT-1A 100 s filter |
|
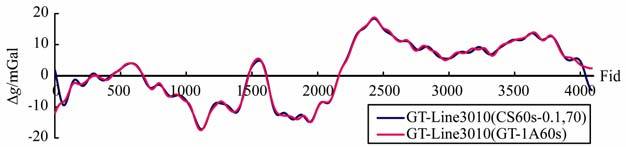
图 7 切比雪夫滤波器与GT-1A系统60 s滤波航空自由空间重力异常对比图 Fig. 7 Airborne gravity free air anomaly of Chebyshev and GT-1A 60 s filter |
|
|
表 1 IIR滤波试验结果与GT-1A系统滤波结果的差值统计 Table 1 The difference between IIR and GT-1A filtering result and statistics |
表 1中给出了图 4~图 7所示的IIR 低通滤波截止波长100s、60s长度航空自由空间重力异常测线数据与GT-1A 系统100s、60s滤波航空自由空间重力异常测线数据(作为标准)的差值比较,即通过两者差值的统计结果来衡量吻合程度.从统计表中看到,两种IIR 滤波器低通滤波结果的差异值都在±1mGal左右,均方差值则多数为0.3~0.4mGal, 吻合程度比较好,与汉宁、海明、布拉克曼等几种窗函数法FIR 低通数字滤波器的效果非常接近[3].可见IIR 低通数字滤波器可以在航空重力数据的低通滤波处理中获得与GT-1A系统滤波结果几乎同样满意的滤波效果.
4 结论(1) 巴特沃思(Butterworth)和切比雪夫(Chebyshev)逼近设计的无限脉冲响应(IIR)低通数字滤波器,通过选择合适的截止波长、通带衰减和阻带衰减等滤波参数,可以在航空重力数据的低通滤波处理中发挥重要的作用,并获得与GT-1A 系统滤波结果几乎同样满意的滤波效果.
(2) 为了获得与GT-1A 系统100s、60s低通滤波(平均航速60 m/s)对应的航空自由空间重力异常测线数据,巴特沃思逼近和切比雪夫逼近的 IIR 低通数字滤波器的通带、阻带衰减分别为3dB、50dB 和0.1dB、70dB,截止波长中间值分别为6000m、3600 m 和6000 m、3850 m.所设计的IIR低通数字滤波器的效果与汉宁、海明、布拉克曼等几种窗函数法FIR 低通数字滤波器的效果非常接近.
(3) 在IIR 低通数字滤波器基础上,根据需要可以进一步设计出IIR 高通、带通数字滤波器等:高通滤波器相当于一个全通滤波器减去一个低通滤波器;带通滤波器相当于两个低通滤波器相减.
(4) GT-1A 系统中采用的Kalman等滤波技术在航空重力数据滤波处理中的作用,有待于以后进一步的探索研究.
| [1] | 郭志宏, 熊盛青, 周坚鑫, 等. 航空重力重复线测试数据质量评价方法研究. 地球物理学报 , 2008, 51(5): 1538–1543. Guo Z H, Xiong S Q, Zhou J X, et al. The research on quality evaluation method of test repeat lines in airborne gravity survey. Chinese J. Geophys. (in Chinese) , 2008, 51(5): 1538-1543. |
| [2] | 熊盛青. 我国航空重磁勘探技术现状与发展趋势. 地球物理学进展 , 2009, 24(1): 113–117. Xiong S Q. The present situation and development of airborne gravity and magnetic survey techniques in China. Progress in Geophysics (in Chinese) , 2009, 24(1): 113-117. |
| [3] | 郭志宏, 罗锋, 安战锋. 航空重力数据窗函数法FIR低通数字滤波试验. 物探与化探 , 2007, 31(6): 568–571. Guo Z H, Luo F, An Z F. Experimental researches on FIR lowpass digital filters based on window functions of airborne gravity data. Geophysical and Geochemical Exploration (in Chinese) , 2007, 31(6): 568-571. |
| [4] | 柳林涛, 许厚泽. 航空重力测量数据的小波滤波处理. 地球物理学报 , 2004, 47(3): 490–494. Liu L T, Xu H Z. Wavelets in airborne gravimetry. Chinese J. Geophys. (in Chinese) , 2004, 47(3): 490-494. DOI:10.1002/cjg2.v47.3 |
| [5] | 孙中苗, 夏哲仁, 石磐, 等. 航空重力测量数据的滤波与处理. 地球物理学进展 , 2004, 19(1): 119–124. Sun Z M, Xia Z R, Shi P, et al. Filtering and processing for the airborne gravimetry data. Progress in Geophysics (in Chinese) , 2004, 19(1): 119-124. |
| [6] | 陈玉东. 数字信号处理. 北京: 地质出版社, 2005 . Chen Y D. Digital Signal Processing (in Chinese). Beijing: Geological Publishing House, 2005 . |
| [7] | 王华奎, 张立毅. 数字信号处理及应用. 北京: 高等教育出版社, 2004 . Wang H K, Zhang L Y. Digital Signal Processing and Application (in Chinese). Beijing: Higher Education Press, 2004 . |
| [8] | 孙中苗, 夏哲仁. FIR低通差分器的设计及其在航空重力测量中的应用. 地球物理学报 , 2000, 43(6): 850–855. Sun Z M, Xia Z R. Design of FIR lowpass differentiator and its applications in airborne gravimetry. Chinese J. Geophys. (in Chinese) , 2000, 43(6): 850-855. |
| [9] | 邓自立. 最优滤波理论及其应用——现代时间序列分析方法. 哈尔滨: 哈尔滨工业大学出版社, 2000 . Deng Z L. Optimization Filtering Theory and Its Applications—The Analytic Method of Modern Time Series (in Chinese). Harbin: Harbin Institute of Technology Press, 2000 . |
| [10] | 邓自立. 卡尔曼滤波与维纳滤波——现代时间序列分析方法. 哈尔滨: 哈尔滨工业大学出版社, 2001 . Deng Z L. Kalman Filtering and Wiener Filtering—The Analytic Method of Modern Time Series (in Chinese). Harbin: Harbin Institute of Technology Press, 2001 . |
| [11] | 郭志宏, 刘浩军, 熊盛青. 平面网格位场数据的空间域非线性曲率滤波方法. 地球物理学进展 , 2003, 18(1): 134–137. Guo Z H, Liu H J, Xiong S Q. The nonlinear curvature filtering technique of plane potential grid data in space domain. Progress in Geophysics (in Chinese) , 2003, 18(1): 134-137. |
| [12] | 刘浩军, 薛典军, 郭志宏, 等. 航空物探软件系统研制. 物探与化探 , 2003, 27(2): 146–149. Liu H J, Xue D J, Guo Z H, et al. The development of the aerogeophysical software system. Geophysical and Geochemical Exploration (in Chinese) , 2003, 27(2): 146-149. |
| [13] | 郭志宏. 航空重力数据测量处理方法技术研究. "百人计划"项目研究报告. 北京: 中华人民共和国国土资源部, 2008. Guo Z H. The method and technology research of airborne gravity survey and data processing. "Hundred People Plan" Project Research Report . Beijing: Ministry of Land and Resources of the People's Republic of China, 2008 |
| [14] | Gabell A, Tuckett H, Olson D. The GT-1A Mobile Gravimeter. ASEG-PESA. Sydeny, 2004 |
| [15] | Laboratory of Control and Navigation. GT1A Post Processing Software Introduction, Version 1.5. Moscow State University, 2006 |
 2011, Vol. 54
2011, Vol. 54