2. 中国地质科学院地球物理地球化学勘查研究所,河北 廊坊 065000
2. Institute of Geophysical and Geochemical Exploration, Langfang Hebei 065000, China
固定翼时间域航空电磁法具有采集速度快、高效、可以在人无法到达的地方进行作业等优点,在找矿、环境地质调查等方面具有广泛的应用.但目前对航空瞬变电磁的研究还不够深入[1],其资料数据量庞大、飞行姿态变化、测高不准、没有数据叠加步骤等因素导致资料品质相对较差,除能用简单的球体模型近似反演特殊情况以外[2],实用的航空电磁法反演方法多是基于一维的[3~10].由于航空电磁的数据品质较差,反演模型层数较多时,简单的线性或非线性一维反演方法往往不能得到稳定可靠的反演结果,Ellis(1998)指出了航空电磁的强病态性质[11],因此在资料解释中应给予足够的重视.为了增强反演的稳定性,可在目标函数中加入先验模型约束信息,按照正则化的反演方法[12]进行计算,如Tlbll和Christensen N B(2006)提出一种稳健的一维正则化反演方法[13],完成了频率域直升机航空电磁探测地下水模型解释问题;Brodie 和Sambridge(2006)在研究频率域航空电磁反演中,提出了一种复杂的“整体方式"的一维正则化反演方法[14],该方法利用参考模型、模型在三维空间上的粗糙度和粗糙度统计分布特征等先验信息;Siemon 等(2006)、 Vallee和Smith(2009)利用侧向约束信息(Laterally Constrained Inversion, LCI),分别在频率域[15]和时间域[16, 17]的一维航空电磁资料反演中取得成功.
以上反演方法均假定由高度计得到的飞行高度数据是准确的,但航空电磁工作中,高度计给出的飞行高度数据往往是有一定误差的,GPS 测量误差、飞行过程的震荡、起伏地形或地表植被环境复杂等均可导致高度计数据误差.如果反演使用的高度数据不准确,将会影响解释结果的可靠性.最近,ChristiansenA V 等(2011)用定量模拟的方法研究了航空电磁数据测量中误差的影响[18],给出了不同飞行高度值下的响应曲线,明确指出了飞行高度测量不准确时会影响解释结果,但文章没有给出如何解决飞行高度测量不准的解释方法.另外航空电磁的飞行高度误差有一定的合理范围,也较容易估计,需要在反演中加以利用.如果能得到较准确的飞行高度数据,再进行反演或成像时,可以获得更可靠的结果.常规的处理是在反演之前进行校正处理,如 Andy Green(1998)使用视偶极深度法进行飞行高度校正处理[19],但由于地下介质电阻率无法得知,高度校正没有可靠的依据,校正效果也不是很好.
很多正则化反演算法要根据模型的光滑程度选择不同类型的模型约束方式,除此之外,正则因子的确定也是一个关键的问题,一般需要多次试探和搜索[20],这种方法的计算量很大,并不适用于航空瞬变电磁的海量资料解释.实际反演中,解释人员要根据反演模型的实际情况而定,如果已知地电模型的信息不多时,正则因子可由程序根据模型与数据拟合情况自适应确定[21],反之,可设定地电模型参数变化范围和正则因子大小,而飞行高度值的合理变化范围的估计相对容易一些,本身就适合进行约束反演,否则用过高的和过低的飞行高度进行反演是没有意义的.根据这两种情况,本文提出两个反演方法,第一个是自适应正则化的反演方法,用于模型电阻率信息量较少的时候,正则因子通过自适应的方式获得,用高度计的飞行高度作为反演初始值,初始模型可以使用均匀半空间模型,用奇异值分解法求解反演方程.另一个是参数有上下界限约束的反演方法,可由已知的模型信息确定电阻率的变化范围与正则化因子,并事先设定飞行高度变化范围,从而可用参数有上下界限约束下的有限内存BFGS拟牛顿法[22, 23](Limited-memory quasi-Newton, LMQN)求解约束反演方程.这种约束优化方法不需要计算 Hesse矩阵,也不需要存储迭代矩阵,而仅需记忆 BFGS迭代产生的m个向量(m在3~7之间)对及当前的负梯度方向上产生的搜索方向[24],从而避免了大量的矩阵与向量乘积计算与迭代矩阵存储过程,另外,算法对线搜索的精度要求较低,一般还有超线性收敛的效果,使得该算法能够胜任航空瞬变电磁海量数据反演问题.鉴于我国还没有时间域航空电磁系统,尚无实际资料,论文用固定翼时间域航空电磁的层状介质模型的x、z分量感生电动势响应数据,加入不同水平的随机噪声后,用上述两个方法实现模型参数与飞行高度的同时反演,以同时得到电阻率反演和飞行高度校正结果.
2 反演算法原理假定飞行测量沿x轴,z轴垂直指向地下,飞行高度(也是发射线圈高度)的真值为ht, 接收线圈高度为hr, 位于点(r,0,-hr)处,收发线圈水平距为r.假定地下N层水平均匀介质电导率为σn,(k= 1,2,…,n),层厚度为hk,(k=1,2,…,n-1).设磁偶极子线圈激励下阶跃电流脉冲,根据文献[25, 26],若飞行测线为x轴,忽略位移电流,接收线圈测量的断电后的x和z分量瞬变感生电动势分别为:
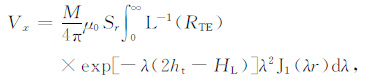
|
(1) |
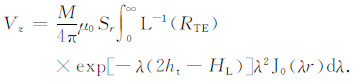
|
(2) |
其中,μ0 为真空磁导率,M为发射磁矩,HL =ht-hr, RTE 是拉普拉斯域中的反射系数,λ 是积分变量,J0 和J1 分别为第一类0 阶和1 阶贝塞尔函数,L-1表示逆拉普拉斯算符,本文采用罗延钟(2003)的GS变换方法[25]计算逆拉普拉斯变换.
2.1 自适应正则化反演方法设d为由X和Z两个分量联合组成的感生电动势数据观测数据,它由Nd=2N个感生电动势观测数据构成:
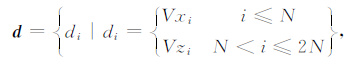
|
(3) |
其中N为接收时间道数.正则化反演可表示为:
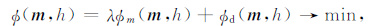
|
(4) |
式中,m表示模型向量,由n层介质的层电阻率自然对数构成,h为飞行高度变量.Φ 为总目标函数,Φm为模型先验约束条件的目标函数:
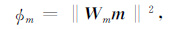
|
(5) |
其中,Wm为约束模型加权矩阵,可选择最小构造模型、最平坦模型和最光滑模型[27].Φd 为观测数据目标函数,线性化后可写为:
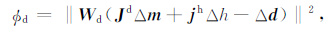
|
(6) |
其中,Wd 为数据加权矩阵,当观测数据误差是独立、不相关的高斯噪声时,Wd 为对角矩阵,对角元为数据标准差的倒数.Jd 为响应数据关于模型参数的雅可比矩阵,jh 为响应数据关于飞行高度参数的雅可比矩阵,Δm和Δh为模型与飞行高度的迭代修正量,计算中变量均使用自然对数值.Δd=d-F(mk-1,hk-1)为理论响应与观测数据误差向量,F为正演算子,正则因子λ 根据数据目标函数与模型目标函数之间的关系定义[21]:
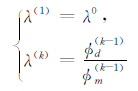
|
(7) |
λ0 为初始正则因子,指标k是指第k次迭代.
由此,最小化目标函数Φ 的问题转化为最小二乘问题:
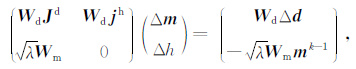
|
(8) |
使用SVD 方法解此方程,便同时得到模型和飞行高度的迭代解.
由于自适应正则化反演方法对初始模型的要求不高,初始电阻率模型可取为电导率-深度成像(Conductivity-Depth Imaging, CDI)结果,或均匀半空间模型或某个先验模型等.但当使用均匀半空间模型做初始模型时,模型目标函数为0,这时用(7)式计算初始正则因子出现困难.在反演前对初始模型进行2~3 次梯度法反演的,可以避免上述情况.反演中雅可比矩阵按链式法则进行,其完整解析计算式见附录.
实际上,飞行高度可以视为发射线圈与地面之间空气层的厚度,若将该空气层视为一维介质的第一层介质,反演飞行高度与反演介质的第一层厚度是一致的,所以飞行高度不准确时,用反演的方法得到上述空气层厚度(也就是飞行高度)理论上是可行的.
2.2 约束反演方法 2.2.1 LMQN 反演方程假定优化反演问题中电阻率参数和飞行高度参数的简单上下限约束为:
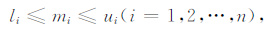
|
(9a) |
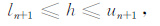
|
(9b) |
本文在使用LMQN 约束反演方法中,先对两个分量数据按如下公式做响应幅值变换:
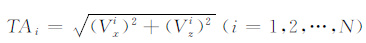
|
(10) |
反演用的观测数据为理论响应幅值变换数据TA加上随机噪声后的自然对数,仍按(4)式定义的正则化反演目标函数进行约束优化反演,其中模型目标函数Φm仍按(5)式定义,而数据目标函数Φd 写为:
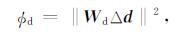
|
(11) |
其中,Δd=d-F(m,h)为理论响应与观测数据误差向量,数据加权矩阵Wd 仍为对角矩阵,为了突出数据的相对误差,对角元修正为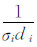
简单上下限约束方式的有限内存拟牛顿约束最优化算法及其收敛性证明等数学研究内容,不是本文的研究主题,具体内容见文献[22, 23],我们的固定翼航空瞬变电磁反演算法是在它的基础上,增加了如上节所述的数据加权和模型加权的步骤.
按照有限内存BFGS 方法[24, 28],假定第k次模型更新为:
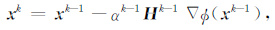
|
(12) |
其中,x是由层电阻率参数m和飞行高度变量h组成的未知向量,αk-1 是用一个合适的线搜索算法得到的步长,我们采用Wolf准则计算:
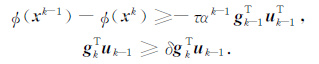
|
(13) |
其中,0<τ≤δ<1,gk-1 =∇Φ(xk-1),T 表示转置,uk=-Hkgk为搜索方向,H为对称正定矩阵,用有限内存BFGS法迭代计算,为了节省内存,假定经过迭代已得到并保存了ns对向量{si=xi+1-xi,yi=gi+1 -gi}i=k-nsk-1及每次迭代的初始Hk,对Hk做了ns次BFGS校正[28],从而得到Hessian矩阵的逆近似Hk.为了保证搜索结果落在(9)式表示的简单界限约束条件,迭代中将sk修正为s′k:
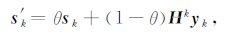
|
(14) |
其中,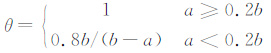
反演迭代的收敛标准为迭代前后目标函数值变化很小或达到某个最大迭代次数为止,梯度向量g的解析计算公式见附录.这种有限内存BFGS 拟牛顿法解简单界限约束问题在解大规模约束问题时可以节省内存,适用于多参数的反演问题,因此可应用在层数目较大、采样时间个数多的航空瞬变电磁一维反演或者高维地球物理参数反演中.
3 模型反演算例根据以上方法,我们用C++ 语言编制了反演程序.反演试算的系统参数为:发射磁矩30×104 Am2,断电时间为12ms, 延时0.01ms时开始采样,40个采样点,发射线圈高度(即真实飞行高度)为120m, 接收线圈高度为70 m, 有效面积为100m2,收发线圈水平距为100m.正演计算x、z分量感生电动势数据中,飞行高度作为一个变量是可以变化的,但收发线圈相对位置保持不变.假定理论模型为一个6层模型,层电阻率分别为50,10,50,10,50,10Ωm, 层厚度分别为48.9522,50.4,76.3178,80.4716,94.5948m.两种反演算法均采用该模型,系统参数及采样时间序列均相同,分别将模型离散成由多个小层构成的模型,再进行反演.以下反演结果中的相对误差是反演结果模型的响应数据与真实模型的响应数据(不含噪声)之间的相对误差,计算公式为
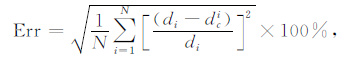
|
其中,d是含噪声的观测数据,dc是反演结果模型的响应数据.
3.1 自适应正则化反演试算为了使用自适应反演,将模型划分成63 个小层,第一层厚度为1.1 m, 层厚等比增加,等比因子为1.05.
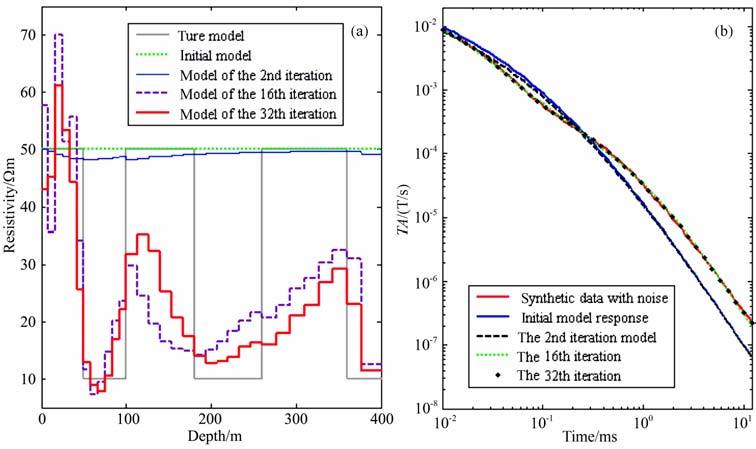
图 1为最平坦模型约束下x、z分量感生电动势数据反演过程中的几次迭代结果和飞行高度反演迭代变化曲线.其中,初始飞行高度值取为115 m, 反演初始均匀半空间模型的电阻率为50Ωm, 经过3次带飞行高度反演的梯度法迭代得到的模型作为新的初始模型,飞行高度梯度法迭代结果为116.616 m, 作为反演的初始飞行高度值.由图可见,经过30 次迭代,电阻率参数反演结果较好地显示了介质的高-低-高-低-高-低的垂向变化.随迭代的进行,反演结果稳步向真值逼近,除最底下的高阻层受两侧低阻层的影响,反演的电阻率值稍偏低外,其他各层的电阻率反演结果均很好;飞行高度值在迭代第10 次后,反演结果为119.696m, 与真值仅偏低0.3m 左右,随后反演迭代基本稳定地收敛到真实飞行高度值,至第30次迭代,飞行高度值反演结果为119.931m, 与真值的误差不足7cm.说明本文方法能在反演电阻率的同时,也很好地校正飞行高度值.
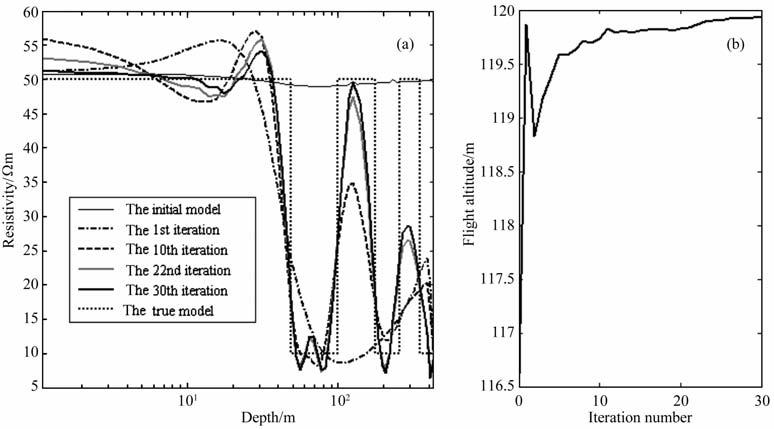
|
图 1 6层模型的反演结果 (a)电阻率反演结果;(b)飞行髙度反演结果. Fig. 1 Inversion results of the 6-layered model (a) Inversion results of resistivity ;b) Inversion results of flight altitude. |
图 2为反演第30次迭代反演结果模型的x、z分量感生电动势响应、理论模型x、z分量响应和初始模型x、z分量响应瞬变曲线对比图.反演结果的数据曲线均与观测数据曲线拟合得较好,由图 2 各次迭代的数据相对误差变化曲线(右图)可知,相对误差是单调下降的,第30次迭代结果的数据拟合相对误差为0.01469%,图 3 也显示了反演迭代过程中,正则因子、数据函数和总目标函数曲线是基本稳定下降的,而模型函数经过平滑化约束作用,由近乎均匀半空间的初始模型迭代为与真实模型接近的平滑化模型,因此模型目标函数稳定较快,模型目标函数值没有发生剧烈变化,反演结果的确逐步逼近真实模型的特点.
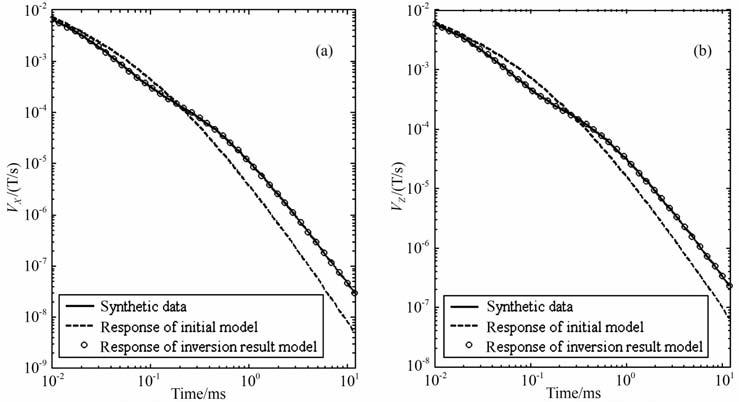
|
图 2 理论模型、初始模型与反演结果模型的瞬变响应曲线对比图 (a) X分量感生电动势;(b) Z分量感生电动势. Fig. 2 The comparison diagrams of transient response curves of theoretical model, initial model and result model of inversion (a) and (b) are X- and Z- component voltage respectively. |

|
图 3 自适应正则因子(a)、目标函数值(b)和数据拟合相对误差(c)的迭代曲线 Fig. 3 Iteration curves of adaptive regularized factor(a) ,objective function value(b) and relative error of data titting(c) |
为了研究噪声对反演结果的影响,按文献[29]的方法在x、z分量感生电动势响应数据中加入高斯噪声,即在t时刻的响应数据中加入标准差为
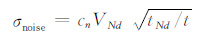
|
(15) |
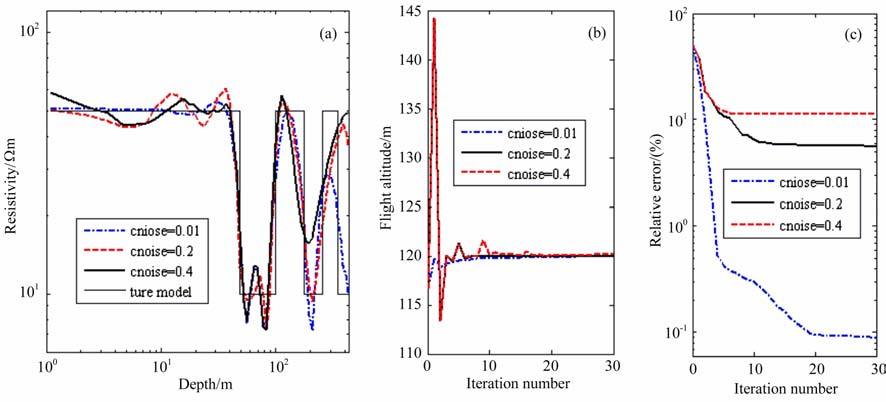
的随机噪声,其中,cn为常数,用于度量噪声的大小.tNd和VNd分别表示最后一个(第Nd个)延时及该时刻的理论响应值.加入这种噪声信号后观测数据表现为晚期信噪比低的特征,与实际情况相符.数据中分别加入cn=0.01、0.2和0.4的噪声,其他反演参数同上.图 4a为真实模型、反演初始模型和三种噪声条件下的第30 迭代结果模型对比,图 4b为三种噪声条件下飞行高度反演迭代曲线对比,图 4c为三种噪声条件下,迭代结果与理论响应之间相对误差曲线对比,图中标示的cnoise值表示在数据加入对应噪声常数值时的反演结果.对比分析可知,噪声对反演结果产生影响,影响程度与数据的噪声水平高低有关.浅部介质电阻率反演结果主要受控于测量早期信号,早期数据的信噪比相对较高,不同噪声水平下的反演结果均较好;但因为晚期信号的信噪比较差,深部介质反演结果的误差就高一些,如当cn=0.4 时,信噪比差的晚期数据致使深层介质电阻率反演结果稍偏高,而噪声较小的cn=0.01 时,基底层的电阻率反演结果很理想,在cn=0.2时,基底层介质电阻率反演结果与cn=0.4 时的结果类似,但基底的低阻特性更明显,效果稍好一些.而三种噪声水平对飞行高度反演结果的影响相对较小,噪声常数cn=0.01时,7次迭代后高度值反演结果的误差即小于0.4m, 随后即稳步向真值逼近,第30次迭代结果为119.931 m, 继续迭代还能得到更好的结果;而噪声常数分别为0.2和0.4时,飞行高度值的前几次迭代结果会发生波动,10次迭代后趋于稳定,第30次迭代后,cn=0.2和0.4时的反演结果分别为119.913m 和120.139m, 均有较好的表现.数据相对误差曲线均是基本稳定衰减的,与没有噪声时的结果(右图)不同的是,相对误差曲线受数据中有噪声的影响而在若干次迭代后会很快稳定下来,如cn=0.01、0.2 和0.4 时第20 次迭代的相对误差分别为0.094%、5.598% 和11.208%,继续迭代不会有明显改进.总之,在上述三种不同噪声水平条件下,算法是稳定的,没有发生反演结果剧烈变化的情况,均能较好地重构介质电阻率和飞行高度值.
|
图 4 不同噪声水平下的反演结果 (a)第30次迭代结果模型;(b)各次迭代的飞行髙度值反演迭代曲线;(c)反演数据与不含噪声的理论响应数据之间的拟合相对误差的迭代曲线. Fig. 4 Inversion results with respect to various noises levels (a) The result models of the 30th iteration;b)The result curves of flight altitude for each iteration; (c) The relative error curves of inversion data is compared with the synthetic data (no noise added). |
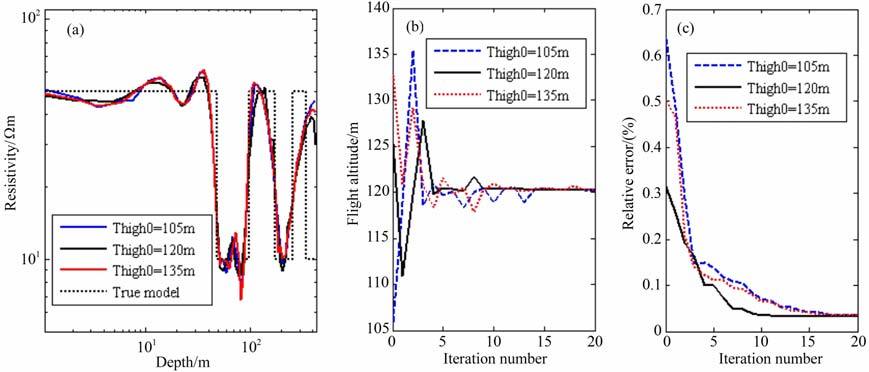
为了分析飞行高度初始值取值不同时的反演效果,假定初始飞行高度Thigh0分别为135m、120m和105m(即飞行高度计具有15 m、0 m 和-15 m的误差)时,用光滑模型约束条件进行反演,观测数据中加入噪声的噪声常数为cn=0.1,其他反演参数同前.图 5 为迭代20 次的结果模型电阻率-深度曲线、飞行高度迭代变化曲线和数据相对误差迭代变化曲线对比图.可见,除受数据噪声影响较大的基底层介质电阻率反演结果偏高外,无论飞行高度初始值是偏高还是偏低,反演结果均较好地重构地下介质电性分布和飞行高度值,第20 次迭代时,飞行高度反演结果分别为120.264、120.251和120.304m, 与真实值的误差约0.3 m, 数据相对误差随迭代次数增加基本保持稳定下降趋势;当反演的飞行高度初始值为准确值时,对基底低阻层的重构效果也相对好一些,飞行高度反演结果经几次迭代后即基本稳定下来,迭代曲线波动幅度也最小,反演结果的数据相对误差也更小,收敛速度相对更快.总之,飞行高度计数据有误差时,将其作为反演高度的初始值,无论该值比真实值高还是低,本文的反演方法均能同时较好地重构地下电阻率和飞行高度值;另一方面,反演结果也表明,飞行高度初始值有误差时会减慢反演迭代收敛速度,所以实际资料处理时,尽可能要获得准确飞行高度数据.
|
图 5 不同飞行高度初始值下的反演结果 (a)电阻率反演结果;(b)飞行髙度反演结果;(b)相对误差迭代曲线. Fig. 5 Inversion results with different mitial flight altitude (a) The resistivity inversion results; (b) The light altitude inversion results; (c) The iterative curves of relative error. |
在参数为上下限约束的LMQN 优化反演中,为了方便比较,模型由上面的6层模型离散得到,除基底层离散为2个层外,其他层分别等厚度离散为6个小层,得到一个32 层模型,最深的小层界面深度为366.5m.飞行高度初始值为115m, 反演初始模型也取电阻率为50Ωm 的均匀半空间模型.以下的优化算法中,校正次数ns取为6,Wolf搜索准则中因子τ 取为0.08、δ 取为0.5,模型约束均使用最平坦模型约束方式.
为了测试约束反演算法中参数上下限约束和模型约束下的效果,将上述32层模型的理论响应幅值变换数据TA加2%的随机噪声后进行3种情况下的反演实验:第一种是没有参数界限约束和光滑化模型约束(正则因子为0)的无约束反演;第二种是所有层电阻率参数均采用相同的界限约束:[5,70]Ωm, 飞行高度变化范围为110~130m;第三种是将真实电阻率为5Ωm 的层约束上下限分别设为30Ωm 和60Ωm, 真实电阻率为10Ωm 的层约束上下限分别设为5Ωm 和25Ωm, 飞行高度参量变化范围为115~125m.第三种比第二种约束方法对应的可行域范围小.后两种情况的正则因子取为0.0001.程序最大反演次数设为32次,三种反演结果在图示中分别标识为C1、C2和C3.图 6 是第二种反演的几次迭代反演结果,图 7是该反演的目标函数衰减与迭代模型的响应数据的相对误差曲线,图 8 则给出了三种反演的飞行高度迭代曲线和第20 次迭代结果模型曲线的对比.
|
图 6 C2约束条件下的几次迭代反演结果.(a)各迭代的模型电阻率反演结果、真实模型与初始模型对比; (b)各迭代反演结果模型响应曲线、加噪的理论模型响应曲线与初始模型响应曲线对比 Fig. 6 The results of the constrained inversion under the constraint of C2 condition, (a) The resistivity inversion result, the true mode and the initial model; (b) The response curves of several iteration inversion data, the curve of synthetic data with noise and the curve of initial model data. |
|
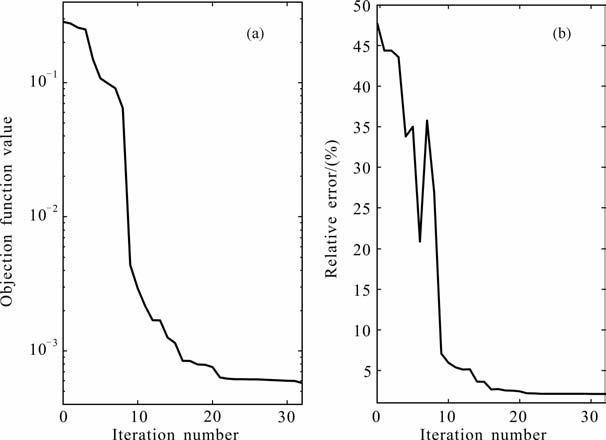
图 7 C2约束条件下的目标函数(a)和相对误差迭代曲线(b) Fig. 7 The teration curves of objective function (a) and the data relative error for the constrained inversion (b) of C2 |
|
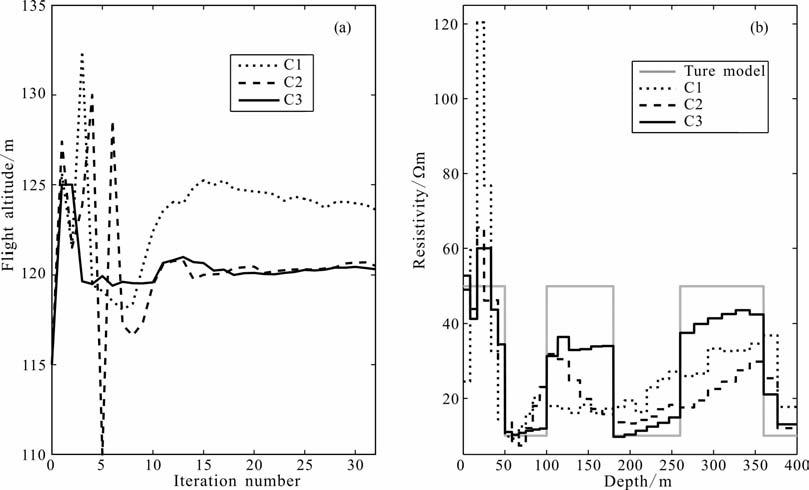
图 8 三种约束下的反演结果 (a)飞行髙度的迭代变化曲线对比;(b)第20次迭代结果模型电阻率分布曲线对比. Fig. 8 The inversion result of the three kind of constrain condition (a) The comparison of the flight altitude curves of each iteration; (b) The comparison of the model resistivity curves of the 20th iteration inversion. |
图 6和7是约束反演迭代的过程细节,反演由均匀半空间模型开始,第二次迭代结果模型与均匀半空间的变化不大,第16次迭代结果模型已经具有真实模型的地电阻率随深度变化的特征.参数约束的作用也反映在图片中,如第三个小层的电阻率受到约束上限70Ωm 的作用、飞行高度值在第5次和第6次迭代中受约束作用而达到了上下限值(如图 8a中的C2曲线),使得结果模型电阻率值始终在可行域中.用没有约束的LMQN 方法(即C1 条件下的反演)时,第3次迭代飞行高度超过130m, 反演结果模型也不光滑,如图 8b.电阻率在第一层中有超过120Ωm 的反演结果,而深部的电阻率反演结果偏低,不能分辨第二个50Ωm 的高阻层段.因此,参数约束起了重要作用.尽管约束反演控制反演参数在给定的带限范围,但目标函数值迭代曲线始终保持单调衰减(见图 7b),使约束反演保持良好的收敛性.随迭代进行,解释模型的响应曲线与观测响应曲线两者逐渐趋于一致(如图 6b),数据相对误差迭代曲线也会基本保持稳定衰减(如图 7b),由于受噪声和约束模型因素影响,会出现局部的非下降情况,但不会影响整体向噪声水平值附近收敛的性质.C3约束条件是对地电模型的先验信息较多情况下的假定条件,如图 8所示,由于它在更小的上下限变化范围内,所以它的约束反演效果比C2 约束更好是必然的,而飞行高度也更快速、稳定地收敛到真值附近,第6~32次迭代中,各次迭代反演结果飞行高度波动范围在119.4~121m 之间,平均值为120.199m, 与真值相差不足0.2 m.第20 次迭代后,三种情况下的数据相对误差分别为3.73227%、2.18659% 和2.03383%;第32次迭代后,三个相对误差值分别为2.17967%、2.1122%和1.96668%,C3条件下的收敛速度快于其他2 种情况.继续迭代下去相对误差仍可以下降,但基于梯度算法的特点和噪声存在的影响,在目标函数极小值点附近反演的收敛速度较慢,本文的方法也不例外.
4 结论实际航空电磁资料中,飞行高度测量值是不准确的,由于飞行高度是发射源到地面之间的空气层的厚度,电阻率和飞行高度同时反演思路是在本质上就是将第一层介质电导率参数固定为空气介质电导率的一维模型反演,因而理论上可行.根据本文对两种飞行高度与电阻率同时反演的算法研究,可以得到如下结论:
(1) 对固定翼时间域航空电磁多分量理论响应资料,自适应正则化反演算法和参数带限约束下的 LMQN约束优化反演算法均可稳定可靠地实现电阻率和飞行高度同时反演,前者适用于对地电模型的先验信息知道不多时的一般情况下的反演,正则化因子是根据模型目标函数值与数据目标函数值的大小关系,用自适应的方法计算得到,后者为反演模型的已知信息较多、可以给出可靠的模型电阻率参数和飞行高度参数变化范围时设计的算法,由模型的光滑度情况设定正则因子,从而应用数学上的带限参数下的有限内存BFGS拟牛顿法进行约束优化反演,使得模型电阻率反演结果在设定变化范围中,飞行高度解释结果也在合理范围内.
(2) 自适应正则化反演算法不需要其他人为参数,只需要给定初始均匀半空间模型的电阻率值和测量的飞行高度作为反演参数初值即可.层状模型的理论响应数据加噪声后的数据反演算例结果表明,无论是飞行高度高于真实值还是低于真实值,反演迭代十几次后层电阻率与飞行高度值均有较好的重构效果;试算了不同水平噪声下的反演,并没有发生因数据噪声水平的变化导致反演结果剧烈变化的情况,反演算法具有良好的稳定性.
(3) 参数带限约束下的LMQN 约束最优化反演方法除利用模型约束外,进一步通过电阻率参数和飞行高度参数的上下限约束方式将迭代解限制在给定的可行域内,并能够保证迭代算法的稳定收敛;算法充分利用了已知的参数约束信息,并根据两种约束方式对反演进行有目的的控制,提高了无约束反演方法的解释效果,使得结果更可靠;由于该方法适用于大规模优化反演问题,故可以用于层数较多、采样数较多的海量资料的航空电磁反演,也可应用于高维模型的地球物理反演问题.
(4) 尽管本文反演算法可以解释测高不准确时的航空电磁资料,但并不意味着飞行高度数据的测量精度高低就不重要,与使用准确的飞行高度作为反演的飞行高度初值进行反演的效果相比,使用错误的飞行高度数据初值会导致反演收敛速度降低,达到相同反演效果时需要更多迭代次数,因此,实际测量数据时还是要尽可能地得到准确的飞行高度数据.
附录 雅可比矩阵及梯度的计算公式在准静态近似下,响应对模型电阻率ρk的导数可通过递推求导得到,即:
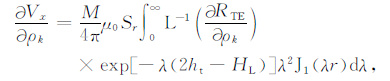
|
(A1) |
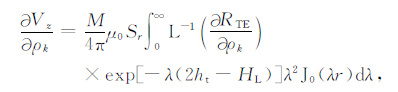
|
(A2) |
其中,
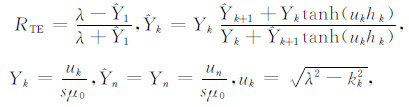
|
s是拉普拉斯变换变量,k是波数.而
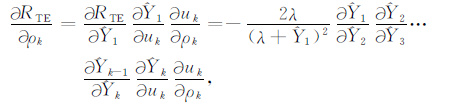
|
(A3) |
其中,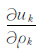
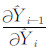
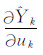
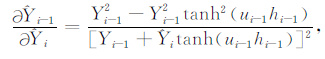
|
(A4) |

|
(A5) |
响应对飞行高度的导数可由下两式给出:
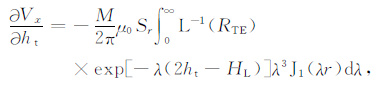
|
(A6) |
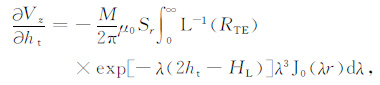
|
(A7) |
梯度向量g中的目标函数对模型电阻率的梯度为:
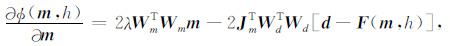
|
(A8) |
其中,Jm是雅克比矩阵中对模型参数求导的子矩阵.梯度向量g中的目标函数对飞行高度h的梯度为:
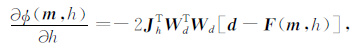
|
(A9) |
其中,Jh是雅克比矩阵中对飞行高度变量求导的子矩阵.
则根据(4)式,雅克比矩阵Jm的元素为:
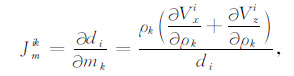
|
(A10) |
雅可比矩阵Jh的元素为:
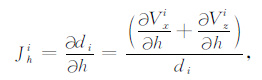
|
(A11) |
衷心感谢评审本文的两位匿名审稿专家的认真审稿并提出宝贵的修改意见.
| [1] | 薛国强, 李貅, 底青云. 瞬变电磁法正反演问题研究进展. 地球物理学进展 , 2008, 23(4): 1165–117. Xue G Q, Li X, Di Q Y. Research progress in TEM forward modeling and inversion calculation. Progress in Geophysics (in Chinese) , 2008, 23(4): 1165-117. |
| [2] | Smith R S, Salem A S. A discrete conductor transformation of airborne electromagnetic data. Near Surface Geophysics , 2007, 5(2): 87-95. |
| [3] | Huang H, Palacky G J. Damped least-squares inversion of time-domain airborne EM data based on singular value decomposition. Geophysical Prospecting , 1991, 39(6): 827-844. DOI:10.1111/gpr.1991.39.issue-6 |
| [4] | 黄皓平, 王维中. 时间域航空电磁数据的反演. 地球物理学报 , 1990, 33(1): 87–97. Huang H P, Wang W Z. Inversion of time-domain airborne electromagnetic data. Chinese J. Geophys. (Acta Geophysica Sinica) (in Chinese) , 1990, 33(1): 87-97. |
| [5] | Chen J, Raiche A. Inverting AEM data using a damped eigenparameter method. Exploration Geophysics , 1998, 29(2): 128-132. DOI:10.1071/EG998128 |
| [6] | 周道卿, 谭林, 谭捍东, 等. 频率域吊舱式直升机航空电磁资料的马奎特反演. 地球物理学报 , 2010, 53(2): 421–427. Zhou D Q, Tan L, Tan H D, et al. Inversion of frequency domain helicopter-borne electromagnetic data with Marquardt's method. Chinese J. Geophys. (in Chinese) , 2010, 53(2): 421-427. |
| [7] | Seiberl W, Ahl A, Winkler E. Interpretation of airborne electromagnetic data with neural networks. Exploration Geophysics , 1998, 29(2): 153-156. |
| [8] | Yin C C, Hodges G. Simulated annealing for airborne EM inversion. Geophysics , 2007, 72(4): F189-F195. DOI:10.1190/1.2736195 |
| [9] | Sattel D. Inverting airborne electromagnetic (AEM) data with Zohdy's method. Geophysics , 2005, 70(4): G77-G85. DOI:10.1190/1.1990217 |
| [10] | 李永兴, 强建科, 汤井田. 航空瞬变电磁法一维正反演研究. 地球物理学报 , 2010, 53(3): 751–759. Li Y X, Qiang J K, Tang J T. A research on 1-D forward and inverse airborne transient electromagnetic method. Chinese J. Geophys. (in Chinese) , 2010, 53(3): 751-759. |
| [11] | Ellis R G. Inversion of Airborne Electromagnetic Data. Exploration Geophysics , 1998, 29(2): 121-127. DOI:10.1071/EG998121 |
| [12] | 王彦飞, 杨长春, 段秋梁. 地震偏移反演成像的迭代正则化方法研究. 地球物理学报 , 2009, 52(6): 1615–1624. Wang Y F, Yang C C, Duan Q L. On iterative regularization methods for migration deconvolution and inversion in seismic imaging. Chinese J. Geophys. (in Chinese) , 2009, 52(6): 1615-1624. |
| [13] | Tlbll R J, Christensen N B. Robust 1D inversion and analysis of helicopter electromagnetic (HEM) data. Geophysics , 2006, 71(2): G53-G62. DOI:10.1190/1.2187752 |
| [14] | Brodie R, Sambridge M. A holistic approach to inversion of frequency-domain airborne EM data. Geophysics , 2006, 71(6): G301-G312. DOI:10.1190/1.2356112 |
| [15] | Siemon B, Auken E, Christiansen A V. Laterally constrained inversion of helicopter-borne frequency-domain electromagnetic data. Journal of Applied Geophysics , 2009, 67(3): 259-268. DOI:10.1016/j.jappgeo.2007.11.003 |
| [16] | Vallée M A, Smith R S. Inversion of airborne time-domain electromagnetic data to a 1D structure using lateral constraints. Near Surface Geophysics , 2009, 7(1): 63-71. |
| [17] | Christensen N B, Reid J E, Halkjr M. Fast, laterally smooth inversion of airborne time-domain electromagnetic data. Near Surface Geophysics , 2009, 7(5): 599-612. |
| [18] | Christensen A V, Auken E, Viezzoli A. Quantification of modeling errors in airborne TEM caused by inaccurate system description. Geophysics , 2011, 76(1): F43-F52. DOI:10.1190/1.3511354 |
| [19] | Green A. Altitude correction of time domain AEM data for image display and geological mapping using the Apparent Dipole Depth (ADD) method. Exploration Geophysics , 1998, 29(2): 87-91. DOI:10.1071/EG998087 |
| [20] | 姚东华, 汪宏年, 陶宏根, 等. 水平层状介质中双侧向测井资料的迭代Tikhonov正则化反演. 地球物理学报 , 2010, 53(9): 2227–2236. Yao D H, Wang H N, Tao H G, et al. Iterative Tikhonov regularization inversion for dual-laterolog in horizontally stratified media. Chinese J. Geophys. (in Chinese) , 2010, 53(9): 2227-2236. |
| [21] | 陈小斌, 赵国泽, 汤吉, 等. 大地电磁自适应正则化反演算法. 地球物理学报 , 2005, 48(4): 937–946. Chen X B, Zhao G Z, Tang J, et al. An adaptive regularized inversion algorithm for magnetiotelluric data. Chinese J. Geophys. (in Chinese) , 2005, 48(4): 937-946. |
| [22] | Byrd R H, Lu P H, Nocedal J, et al. A limited memory algorithm for bound constrained optimization. SIAM Journal on Scientific and Statistical Computing , 1995, 16(5): 1190-1208. DOI:10.1137/0916069 |
| [23] | Ni Q, Yuan Y. A subspace limited-memory quasi-Newton algorithm for large-scale nonlinear bound constrained optimization. Mathematics of Computation , 1997, 66(220): 1509-1520. DOI:10.1090/S0025-5718-97-00866-1 |
| [24] | Nocedal J. Updating quasi Newton matrices with limited storage. Math. Comp. , 1980, 35(151): 773-782. DOI:10.1090/S0025-5718-1980-0572855-7 |
| [25] | 罗延钟, 张胜业, 王卫平. 时间域航空电磁法一维正演研究. 地球物理学报 , 2003, 46(5): 719–724. Luo Y Z, Zhang S Y, Wang W P. A research on one-dimension forward for aerial electromagnetic method in time domain. Chinese J. Geophys. (in Chinese) , 2003, 46(5): 719-724. |
| [26] | Nabighian M N. Electromagnetic Methods in Applied Geophysics (Volume 1, Theory). Tulsa: Society of Exploration Geophysicists, 1988 |
| [27] | Farquharson C G, Oldenburg D W. Inversion of time-domain electromagnetic data for a horizontally layered earth. Geophys. J. Int. , 1993, 114(3): 433-442. DOI:10.1111/gji.1993.114.issue-3 |
| [28] | Liu D C, Nocedal J. On the limited memory BFGS method for large scale optimization. Mathematical Programming B , 1989, 45(1-3): 503-528. DOI:10.1007/BF01589116 |
| [29] | Munkholm M S, Auken E. Electromagnetic noise contamination on transient electromagnetic soundings in culturally disturbed environments. J. Environ. Eng. Geophys , 1996, 1(2): 119-127. DOI:10.4133/JEEG1.2.119 |
 2011, Vol. 54
2011, Vol. 54


