Rayleigh波是沿地表传播的一种弹性波,从1953年Haskell最初提出传播矩阵方法[1]后,人们对瑞利面波的理论研究以及应用研究不断深入.近年来,瑞利面波法已开始在地球物理勘探、超声无损检测等领域得到了大量的研究和应用[2, 3].在 Rayleigh波频散曲线的计算方面,为改进Haskell方法的高频不稳定性,出现了Schwab-Knopoff方法[4, 5]、δ 矩阵法[6]、Abo-Zena 方法及其改进方法[7~9]等.1993 年,陈晓非提出广义反射透射系数法[10],彻底解决了这一问题.Pei等[11]在2008 年改进了广义反射透射系数的计算方法,从而在一定程度上减少了计算量.何耀锋等[12]在2006 年提出了久期函数族的概念,避免了广义反射透射系数法在求解含低速层模型对应频散曲线时丢根的问题.
在实际应用中,当层状介质中存在低速层时,提取到的频散曲线往往会发生“之"字形回折,这与理论计算得到的频散曲线不同,因而在一定程度上造成了反演解释中的困难.这种现象已受到很多学者的关注,1991年,黄嘉正初步分析了“之"字形频散曲线的机理[13].张碧星等于2000 年对“之"字形频散曲线进行了解释[14],但在高频段仍与实际不符,进而在2002年从能量角度讨论了“之"字形频散曲线的形成机理,较好地解释了“之"字形频散曲线形成的原因[15].2003年,Forbriger提出了一种反演方法避免“之"字形频散曲线造成的限制[16, 17],Lu 等在2007年基于“之"字形频散曲线的形成机理提出了利用“之"字形频散曲线的反演方法[18].“之"字形频散曲线的“起跳点"(发生“之"字形回折的点)频率在一定程度上显示了介质的性质.但是,目前还没有人研究“之"字形频散曲线“起跳点"频率与哪些参数有关,而搞清楚这一问题有利于在实际应用中基于“之"字形频散曲线对介质参数的定性分析.本文将研究不同震源和介质参数对频散曲线起跳点的影响.
2 “之"字形频散曲线起跳点位置的确定Zhang等人在1996 年改进了Abo-Zena方法,得到传递矩阵算法公式[19].基于这一算法,在给定震源作用下,频散曲线各模式r方向和z方向的激发强度(即位移,其平方与能量成正比,因此可以用于研究不同模式的能量大小)计算公式如下[15]:
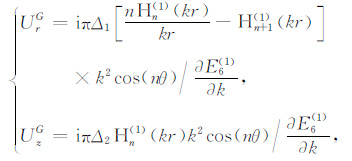
|
(1) |
其中k为波数,θ 为与震源夹角,Hn(1),Hn+1(1) 为汉克尔函数,n为与震源类型有关的系数,当震源为爆炸点源和竖直集中力时为0,震源为水平集中力时为1.Δ1,Δ2 分别为(2)式右边的分子[18, 19]:
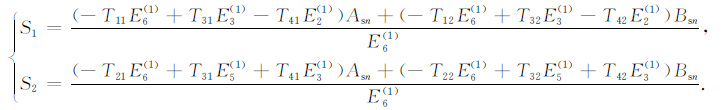
|
(2) |
Asn,Bsn是与震源类型相关的系数,E1(1) ~E6(1) 分别为文献[19]中传递矩阵算法计算得到的第1层对应向量E(1)的6个元素,而其中E6(1) = 0 为Rayleigh波特征方程.Tij(i=1,2,3,4;j=1,2)为与震源有关的矩阵元素.
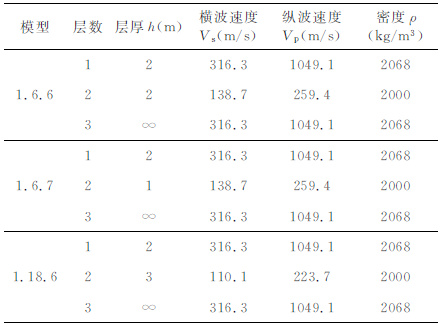
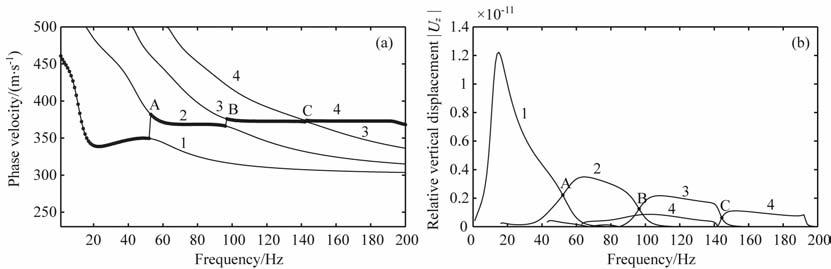
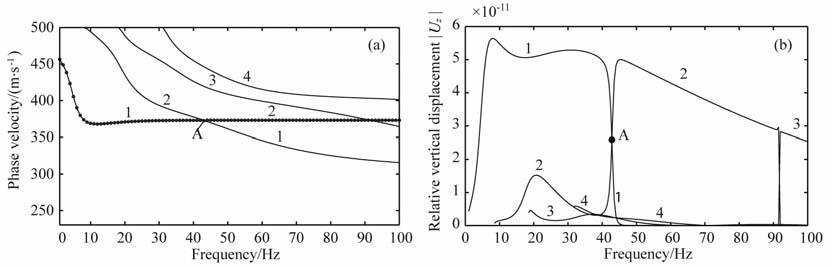
以表 1中含低速层的三层模型为例,在竖直集中力作用下,其频散曲线及其前4 阶模式对应竖直方向的位移如图 1(a, b)所示.由于能量由位移确定,因此可以利用位移来研究Rayleigh波的激发能量.由图 1b,在低频处第1 阶模式的激发能量占主导地位,而随着频率的升高,当频率超过约52.1 Hz时(即A 点),第2 阶模式的激发能量占主导地位.由文献[15]中对于“之"字形频散曲线形成机理的研究,“之"字形频散曲线为各频段激发能量占主导地位的模式对应频散曲线的连线.因此,此时实际提取的“之"字形频散曲线在频率低于52.1Hz的区域为基阶模频散曲线,而频率高于52.1 Hz时为第1高阶模频散曲线,即图 1a中第2条频散曲线.可见频散曲线在图 1b中点A 对应的频率处发生了“之"字形回折,即A 点对应的频率为表 1中模型在竖直集中力作用下“之"字形频散曲线的第1个“起跳点"对应的频率.而点B和点C 对应频率分别为第3,4阶模式激发能量开始占主导地位时的频率,因此点A,B,C 对应的频率即为表 1中模型在竖直集中力作用下对应“之"字形频散曲线的前三个“起跳点"频率.基于点A,B,C 确定的“起跳点"频率即可得到理论上的“之"字形频散曲线如图 1a中的圆圈所示.
|
图 1 表 1中模型对应的频散曲线 (a)频散曲线,其中圆圈为"之"字形频散曲线;(b)各模式激发强度. Fig. 1 Dispersion curves corresponding to the medium in Table 1 (a) Dispersion curves, the circles represent the ‘zigzag’ dispersion curve; (b) Displacement spectrum. |
|
|
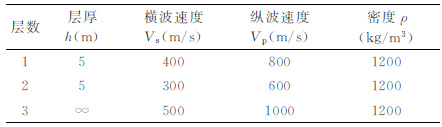
表 1 含低速层的三层介质模型 Table 1 Three 1 ayer medium with low velocity 1 ayer |
与此类似的,在后面的研究中,将计算各模式竖直方向的位移,利用不同模式激发强度开始占主导地位时的频率来确定“之"字形频散曲线“起跳点"的频率.具体做法是,画出各模式的激发强度曲线,在曲线交叉点(例如图 1b中点A,B,C)附近对频率进行加密,以得到较为精确的交叉点对应频率,即可得到“起跳点"的频率.以此研究各参数与“之"字形频散曲线“起跳点"频率的关系.
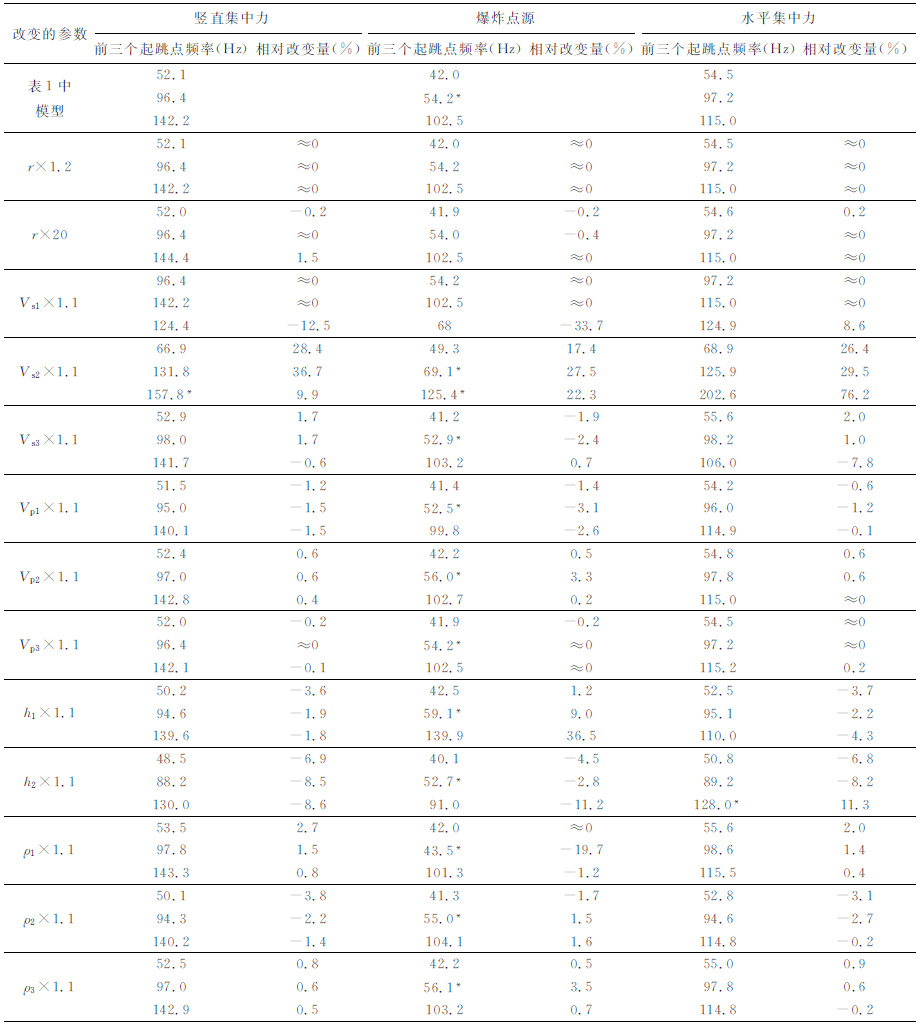
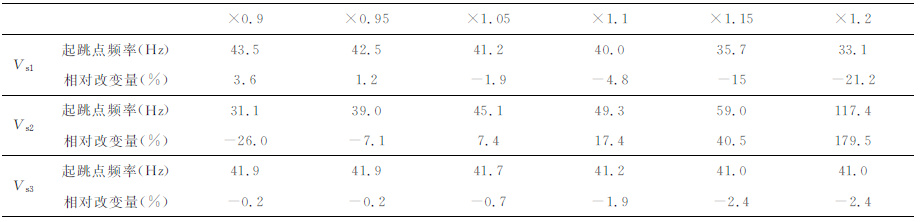
3 影响“之"字形频散曲线起跳点位置的物理量从公式上来看,与“之"字形频散曲线起跳点位置有关的物理量包括:介质各层的横波速度、纵波速度、层厚、密度、与震源距离r,另外震源类型也会对起跳点位置产生影响.以表 1 中含低速层的三层模型为例,分别计算在三种不同的震源激发下r=1m处对应的“之"字形频散曲线前三个起跳点对应的频率,并且在保持其他参数不变的情况下分别改变表 1中模型各参数计算其在不同震源下对应频散曲线起跳点频率,考察其变化情况,如表 2 所示.震源均为处在r=0 处的δ函数,竖直和水平集中力处于z=0处,爆炸点源处于z=3m 处.其中起跳点频率相对改变量的计算公式为

|
(3) |
|
|
表 2 改变表 1中模型参数后在不同震源下的起跳点频率 Table 2 Jump point frequencies after the parameters in Table 1 are changed for different sources |
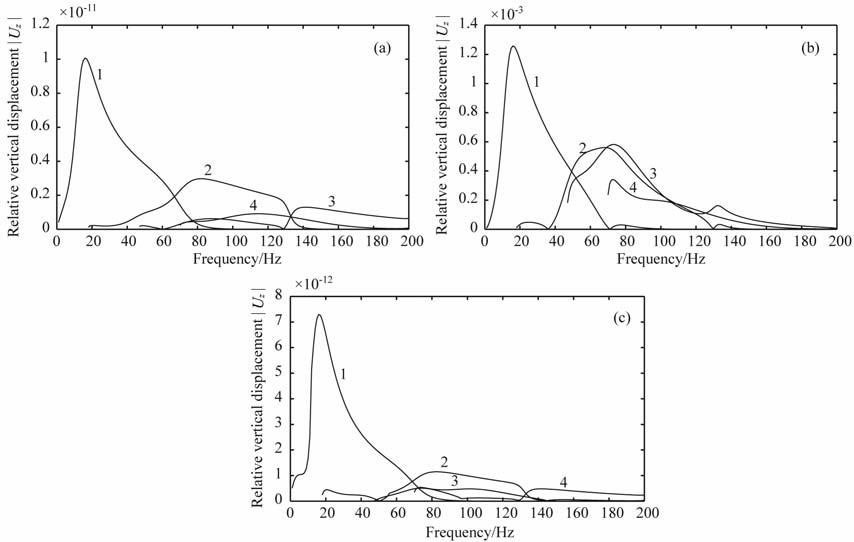
图 1b,2a,2b分别为表 1中模型在竖直集中力、爆炸点源、水平集中力作用下前4 阶模式竖直方向的位移;图 3(a~c)分别为表 1中模型第2层横波速度增加10%后在竖直集中力、爆炸点源、水平集中力作用下前4阶模式竖直方向的位移.从图 1 中可以看出,在很大范围的频率下,爆炸点源和水平集中力所激发的各模式能量除基阶模外差别不大,因此在介质参数改变时,起跳点位置的变化并不规律.而且在一些频段下,由于几阶模式的能量相近,实际提取的频散曲线应为几条频散曲线综合得到的[15],此时仅以不同模式激发强度的大小变化判断频散曲线的起跳点并不准确.表 2 中带星号的数表示此时忽略了这样一些并不明显的起跳点.这种情况下仅仅研究频散曲线起跳点的意义不大.

|
图 2 表 1中模型对应的频散曲线各模式的激发强度.其中(a),(b)分别对应爆炸点源和水平集中力作用下的情况 Fig. 2 Displacement spectrum of the medium in Table 1 for (a) explosive point source; (b) horizontal point force |
|
图 3 表 1中模型第2层横波速度增加10%后对应频散曲线各模式的激发强度,其中(a)~(c)分别对应竖直集中力、爆炸点源、水平集中力作用下的情况 Fig. 3 Displacement spectrum after adding 10% to the S-wave velocity of second layer of the medium in Table 1 for (a) vertical point force; (b)explosive point source; (c) horizontal point force |
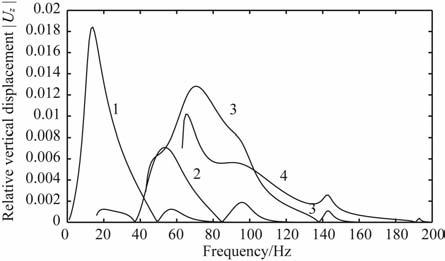
如表 1 中所示,当r增加20%,即在距离震源1.2m 处,提取的频散曲线与原频散曲线的起跳点位置几乎没有区别.而当r扩大20倍时,起跳点频率的变化也很小.考察竖直方向位移的计算公式(1),r仅在汉克尔函数中出现,由于频散曲线起跳点的频率取决于同频率不同模式之间的大小对比,而由汉克尔函数的特点,其受到r的影响更小.在爆炸点源下,当r为20m 时各模式的激发强度曲线如图 4所示,与图 2a对比可以看出,尽管随着接收距离的增加各模式的幅值都有所减小,但同频率下各模式之间激发强度的对比变化很小.由公式(1),波数k是和r共同出现的,对于同一波数,当r增大为原来的20倍时,kr的值也为原来的20 倍.也就是说,在一定程度上可以看成kr对频散曲线起跳点位置影响不大.若保持r不变而令k增大为原来的20倍,则汉克尔函数的值相同,但由于k在公式(1)其他部分也存在,起跳点位置的变化情况将与单纯扩大r不同.由此也可以看出,若第一和第二模式在起跳点所在频率的相速度差比本例中更大或更小,其对汉克尔函数的影响与单纯变化r是相同的.因此,不论第一和第二模式在起跳点所在频率下k的差别如何,与震源的距离对频散曲线的起跳点位置影响都极小,在后面的研究中将忽略r的影响.
|
图 4 当r=20 m时表 1中模型对应频散曲线各模式在爆炸点源下的激发强度 Fig. 4 Displacement spectrum of the medium in Table 1 when r=20 m under explosive point source |
从表 2 中可以看到,当将第3 层参数(横波速度、纵波速度、密度)增加10% 时,“之"字形频散曲线起跳点频率的相对改变量几乎全部远小于将前两层参数增加10% 时造成的相对改变量.这说明,“之"字形频散曲线起跳点频率对前两层参数的影响较敏感,而对第3层参数的影响相对不敏感.对于前两层介质的参数,横波速度增加10%对于起跳点频率的影响明显较大,层厚的影响次之,而纵波速度和密度的影响相对较小(但仍比第3 层的参数对起跳点频率的影响要大).这与介质参数对理论频散曲线的影响情况类似[21],但是,所不同的是第3 层即半空间的参数对起跳点的影响总是很小,因此,后面的研究中将只考虑横波速度和层厚的影响.
4 不同震源下频散曲线起跳点位置与介质参数的关系从表 2中可以看出,不同震源对应的起跳点频率是有区别的,下面将更深入研究三种不同震源下起跳点频率与介质参数的关系.由于“之"字形频散曲线上第一个起跳点以后各阶模式能量往往较为复杂,单纯研究这些起跳点意义不大,因此后文中将只研究频散曲线的第一个起跳点.后文中提及的起跳点均为第一个起跳点.
4.1 竖直集中力下起跳点位置与介质参数的关系再次以表 1中的介质为基础,分别将其横波速度和层厚改变,而保持其他参数不变,研究其起跳点的相对改变量(相对改变量的计算公式为式(3)).为了更清楚地看出起跳点随介质参数的变化情况,后面的研究中将增加各参数的变化范围,得到新的“之"字形频散曲线起跳点频率及相对改变量.
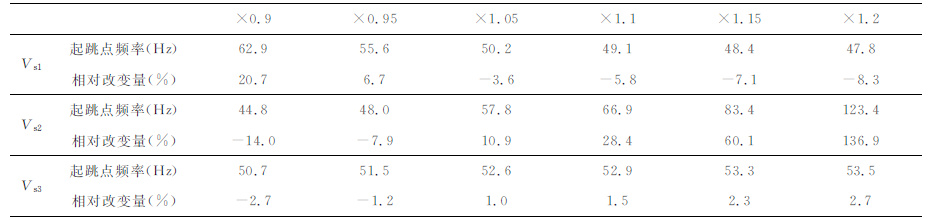
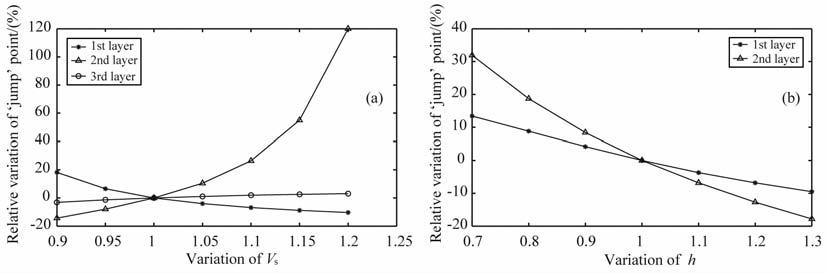
假设介质受到竖直集中力作用,震源为处在z=0,r=0处的δ函数.分别改变表 1中模型各层横波速度并保持其他参数不变,得到新的起跳点频率如表 3所示.起跳点频率随横波速度变化的趋势图如图 5a,可以看到,起跳点频率受第3 层横波速度的影响远小于第1层和第2 层.当第1 层横波速度增加或第2层横波速度减小的时候,起跳点频率降低;反之,起跳点频率升高.这说明,第1层和第2层横波速度越接近,起跳点频率越高;第1层和第2层横波速度差别越大,起跳点频率越低.而且,从图中可以看到,当第1层横波速度较小或第2 层横波速度较大时起跳点频率的变化速度较快.也就是说,第1层和第2 层横波速度差别越小,起跳点随横波速度变化得越快.
|
|
表 3 改变表 1中各层横波速度后在竖直集中力作用下的起跳点频率,每列代表横波速度(Vs1,Vs2,Vs3)乘以不同倍数后的起跳点频率及相对改变量 Table 3 Jump point frequencies after the S-wave velocities in Table 1 are multiplied by different times under vertical point force, each columnsmeans the jump point frequencies after the S-wave velocities (Vs1,Vs2,Vs3) are multiplied by different times |

|
图 5 竖直集中力作用下起跳点频率改变量随各层参数变化图 (a)起跳点频率随横波速度变化趋势;(b)起跳点频率随层厚变化趋势. Fig. 5 Variation of the jump point frequencies when the parameters of each layer are changed under vertical point force (a) Variation with Vs; (b) Variation with h. |
由前面的研究可知,层厚对起跳点频率的影响比横波速度要小,但是仍然存在较明显的影响.改变表 1中模型前两层厚度,得到竖直集中力作用下新的起跳点频率如表 4 所示.起跳点频率随层厚变化的趋势图如图 5b.当第1层和第2层即低速层的层厚增加时,起跳点的频率都逐渐减小,第2层层厚对起跳点频率的影响程度约为第1 层层厚的二倍.这说明,低速层的埋深(第1 层厚度)和低速层厚度都对起跳点频率有影响,但低速层厚度的影响更大,约为低速层埋深的二倍.由于“之"字形回折主要与低速层有关,而通常频率较低即波长较长的波的穿透深度较深,能反映较深层区域的信息,因此当低速层的埋深增加时,起跳点往往趋于更低的频率.
|
|
表 4 改变表 1中各层厚度后在竖直集中力作用下的起跳点频率,每列代表层厚(h1,h2)乘以不同倍数后的起跳点频率及相对改变量 Table 4 Jump point frequencies after the thicknesses in Table 1 are multiplied by different times under vertical point force, each columns means the jump point frequencies after the thicknesses (h1,h2) are multiplied by different times |
但是,起跳点频率的降低并不是无限度的,而是有一个极限.例如,改变第1层厚度为表 1中模型的4倍,即20m, 其对应频散曲线的能量谱如图 6b,起跳点频率为42.8Hz, 相对改变量为17.9%,并没有很大的变化,也就是说,“之"字形频散曲线起跳点频率不会无限制的降低,随着低速层越来越明显,其改变的速度会逐渐减慢.而且,此时Rayleigh 波的波长约为8.7m, 根据半波长理论其穿透深度约为5m左右,明显小于低速层的埋深,因此尽管起跳点与波的穿透深度存在一定联系,但并不是密切相关的.根据能量最大原则得到的“之"字形频散曲线如图 6a中圆圈所示,A 点为理论上的起跳点.图中前两条理论频散曲线在A 点附近很接近.尽管理论上存在“之"字形回折,但是频散曲线的“之"字形回折现象并不明显.这与图 1a中点C 处的情况类似,尽管理论上存在起跳点,但是实际应用中由于精度的限制很难发现这些点.由于低速层的埋深很深,对地表激发的Rayleigh波在较高频率下受到低速层的影响较小,这造成了实际上很难发现“之"字形回折现象.经过实例计算发现,在爆炸点源和水平集中力作用下也有类似现象.
|
图 6 同图 1,但为表 1中模型第1层厚度变为20 m时 Fig. 6 Same as Fig.1,but for when thickness of the tirst layer of the medium in Table 1 is 20 m |
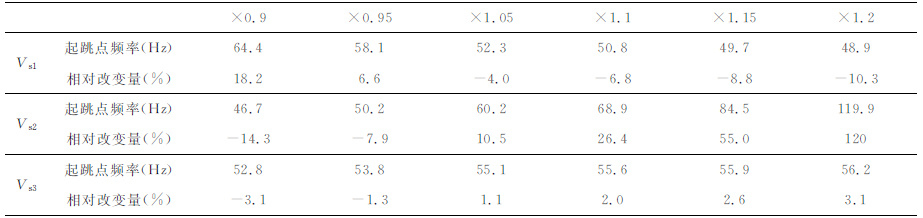
下面假设介质受到水平集中力作用,震源为处在z=0,r=0处的δ 函数.分别改变表 1 中模型各层横波速度,其他参数不变,得到新的起跳点频率如表 5所示.起跳点频率随横波速度变化的趋势图如图 7a,与竖直集中力作用的情况类似,起跳点频率受第3层横波速度的影响远小于第1 层和第2 层.当第1层横波速度增加或第2层横波速度减小的时候,起跳点频率降低;反之,起跳点频率升高.
改变表 1中模型前两层厚度,得到水平集中力作用下新的起跳点频率如表 6 所示.起跳点频率随层厚变化的趋势图如图 7b.与竖直集中力作用情况完全类似的,当第1 层和第2 层即低速层的层厚增加时,起跳点的频率都逐渐减小,第2层层厚对起跳点频率的影响程度约为第1层层厚的二倍.
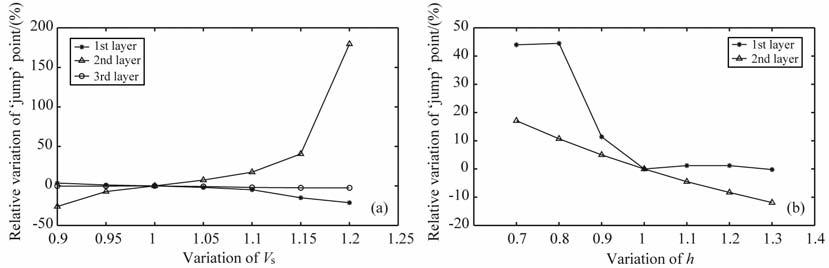
4.3 爆炸点源下起跳点位置与介质参数的关系假设介质受到爆炸点源作用,震源为处在z=3m, r=0处的δ 函数.分别改变表 1中模型各层横波速度,其他参数不变,得到新的起跳点频率如表 7所示.起跳点频率随横波速度变化的趋势图如图 8a,与竖直集中力作用的情况类似,起跳点频率受第3层横波速度的影响远小于第1层和第2层.当第1层横波速度增加或第2 层横波速度减小的时候,起跳点频率降低;反之,起跳点频率升高.这说明,第1层和第2层横波速度越接近,起跳点频率越高;第1层和第2层横波速度差别越大,起跳点频率越低.而且,当第1层横波速度较小或第2 层横波速度较大时起跳点频率的变化速度较快.也就是说,第1层和第2层横波速度差别越小,起跳点随横波速度变化得越快.
注意到这种情况下第3层横波速度增大或减小时起跳点的频率均有所降低.由于起跳点的频率是由同频段各阶模式激发能量之间的大小对比决定的,当参数改变时,各阶模式的激发能量都有所变动,这造成了起跳点频率随参数的变化趋势并不是绝对单调的.由此也可以看出,“之"字形频散曲线与介质参数的关系是非线性的,因此尽管通过本文的研究表明频散曲线的起跳点频率与介质参数的关系在一定程度上是近似单调的,但本质上它们之间的关系还是非线性的.而且,由于“之"字形频散曲线与介质参数的关系是非线性的,这也造成了频散曲线的反演问题是非线性的.
改变表 1中模型前两层厚度,得到爆炸点源作用下新的起跳点频率如表 8 所示.起跳点频率随层厚变化的趋势图如图 8b.与竖直集中力作用情况类似的,当第1层和第2层即低速层的层厚增加时,起跳点的频率逐渐减小.
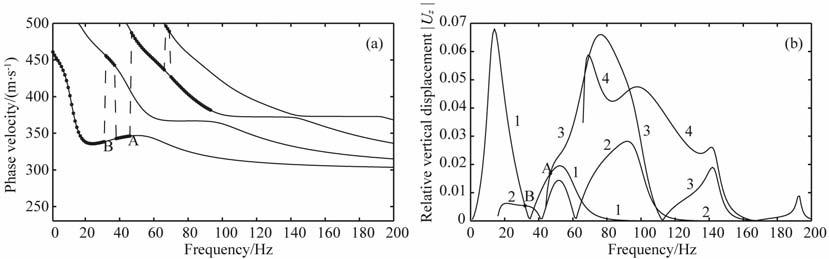
但是,当改变第1层厚度时,起跳点频率的变化情况比较特别.事实上,当第1层厚度变为4.5m 时各模式激发强度如图 9b所示,与图 2a对比发现各模式激发强度的变化较为复杂,因此起跳点频率随第1层厚度的变化趋势不如竖直和水平集中力震源情况规律.而且由“之"字形频散曲线的成因,根据各阶模式的激发强度对比得到的“之"字形频散曲线如图 9a中圆圈所示.可以看到理论上在图中点B应为频散曲线的起跳点,但是由于在B 点处只产生了较短的“之"字形回折,且由图 9b可知在这一频段前两阶模式的激发强度都不是很大,实际应用中由于误差原因不容易发现该处回折点,因此这里选取了A点作为起跳点.如前面所说,“之"字形频散曲线与介质参数的关系是非线性的.而当第1层厚度增加时,起跳点的频率改变已经接近极限,事实上当第1 层厚度变为20m 时起跳点频率为42.7Hz, 如前面所述,此时随第1层厚度增加,起跳点频率实际上在极限频率附近震荡,但是改变很小.
|
图 9 同图 1但为表 1中模型第1层厚度变为4.5 m时 Fig. 9 Same as Fig.1, but for when thickness of the first layer of the medium in Table 1 is 4.5 m |
相对来说,爆炸点源作用下起跳点频率随介质参数的变化规律与竖直和水平集中力的情形有一些区别.但是,尽管不同的震源作用下起跳点频率稍有不同,它们都遵循着类似的规律:当第1层横波速度增加或第2层横波速度减小的时候,起跳点频率降低,反之起跳点频率升高;当第1层和第2层即低速层的层厚增加时,起跳点的频率都逐渐减小.
尽管前面的研究主要基于第2层为低速层的三层介质,但是,当介质含有更多层时,利用类似于文献[22]中方法,可将低速层上面各层及下面各层分别加权平均成一层,近似成为一个三层的介质,其频散曲线与原频散曲线差别不大,因此,前面研究的结论对于含低速层的多层介质也可近似成立,即:起跳点频率随低速层横波速度的减小或低速层以上层横波速度的增大而降低,反之升高;起跳点频率随低速层厚度或埋深(低速层以上层的总厚度)的增大而降低,反之升高.
5 数值模拟在这一部分,我们利用有限元在数值上模拟验证有效性.对于表 9中的各模型,利用有限元方法模拟其在竖直圆盘形震源激励下(当离震源较远时,可近似看成竖直集中力震源)的24 道时域波形(详细建模情况见文献[23]),并利用f-k域方法按能量最大原则提取频散曲线如图 10.
|
|
表 9 三个含低速层的三层介质模型 Table 9 3-layer media with low velocity layer |
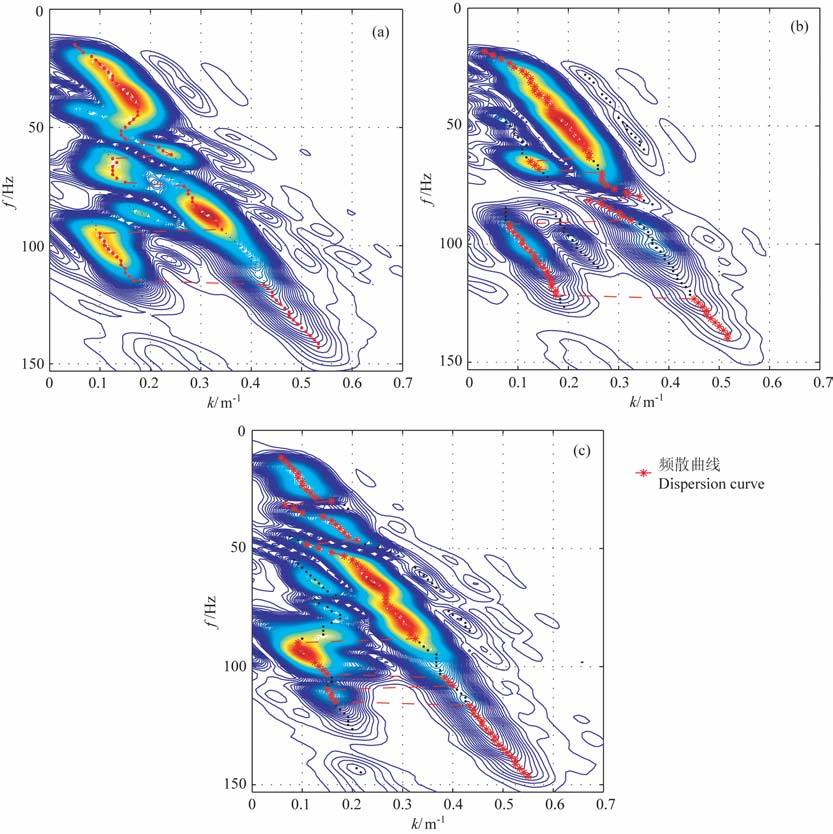
|
图 10 f-k域能量谱及频散曲线 (a)模型 1.6.6;(b)模型 1.6.7;(c)模型 1.18.6. Fig. 10 Displacement spectrum obtained by f-k transformation and dispersion curves (a) Model 1.6.6; (b) Model 1.6.7; (c) Model 1.18.6. |
模型1.6.7与1.6.6相比,第2层即低速层厚度由2m 减为1m.由图 10a,10b可知,模型1.6.6对应“之"字形频散曲线的起跳点频率为42.6 Hz, 模型1.6.7对应“之"字形频散曲线的起跳点频率为65.3Hz.这与前面的结论“起跳点频率随低速层厚度的减小而升高"是相符合的.模型1.18.6 与前两个模型相比,低速层厚度更厚而且横波速度更低,由图 10c可知模型1.18.6对应“之"字形频散曲线的起跳点频率为26.6Hz, 低于前两个模型,这印证了本文前面的结论.
基于本文的结论,在一些实际工程中可以直接通过起跳点频率的高低判断所检测对象是否符合标准.例如,在利用Rayleigh波进行路基压实度检测当中[24],往往需要研究整条路面上很多区域的频散曲线,然后分析所有的频散曲线以找出压实度不够大(即横波速度较小)的区域.而利用本文中的结论,直接找出对应频散曲线起跳点频率明显较低的区域即可.
6 结论本文通过实例研究了“之"字形频散曲线起跳点(特别是第一个起跳点)对应频率与震源、检波器和震源的距离、介质各层参数的关系,发现“之"字形频散曲线起跳点对应频率与检波器和震源距离几乎无关,但与震源和介质各层参数有关.尽管震源的不同会影响提取的“之"字形频散曲线起跳点频率,但是对于相同震源,起跳点频率随介质参数的变化情况都有着相同的规律:
(1) 对频散曲线的起跳点频率影响最大的是低速层和低速层以上层的横波速度,其次是层厚;
(2) 纵波速度、密度以及低速层以下各层的参数对频散曲线的起跳点频率影响较小;
(3) 起跳点频率随低速层横波速度的减小或低速层以上层横波速度的增大而降低,反之升高;
(4) 起跳点频率随低速层厚度或埋深(低速层以上层的总厚度)的增大而降低,反之升高.
从频散曲线的激发能量谱也可以看出,“之"字形频散曲线与介质参数的关系实际上是非线性的,而这也造成了反演问题的非线性.尽管本文的研究发现频散曲线起跳点频率与介质参数之间存在一定近似单调的关系,但本质上两者之间的关系仍然是非线性的.
根据本文的结论,可以在一些实际应用中(如路基压实度的检测等)利用“之"字形频散曲线起跳点频率的高低来定性判断介质中低速层的层厚或横波速度的大小.
| [1] | Haskell N A. The dispersion of surface waves on multilayered media. Bull. Seism. Soc. Am. , 1953, 43: 17-34. |
| [2] | Clark A V, Fuchs P, Schaps S R. Fatigue load monitoring in steel bridges with Rayleigh waves. J. Nondestruct. Eval. , 1995, 14(3): 83-98. DOI:10.1007/BF01183114 |
| [3] | Nadal M H, Tardy F, Gondard C. Impulse modeling of the Rayleigh wave propagation generated by a spherical focused transducer. J. Nondestruct. Eval. , 1998, 17(4): 179-190. |
| [4] | Schwab F. Surface-wave dispersion computations: Knopoff's method. Bull. Seism. Soc. Am. , 1970, 60: 1491-1520. |
| [5] | Schwab F, Knopoff L. Fast surface wave and free mode computations. In: Bolt B A ed. Methods in Computational Physics. New York: Academic Press, 1972 : 87 -180. |
| [6] | Buchen P W, Ben-Hador R. Free-mode surface-wave computations. Geophys. J. Int. , 1996, 124(3): 869-887. DOI:10.1111/gji.1996.124.issue-3 |
| [7] | Abo-Zena A. Dispersion function computations for unlimited frequency values. Geophys. J. R. Astr. Soc. , 1979, 58(1): 91-105. DOI:10.1111/j.1365-246X.1979.tb01011.x |
| [8] | Menke W. Comment on 'Dispersion function computations for unlimited frequency values' by Anas Abo-Zena. Geophys. J. R. Astr. Soc. , 1979, 59(2): 315-323. DOI:10.1111/j.1365-246X.1979.tb06769.x |
| [9] | 李幼铭, 束沛镒. 层状介质中地震面波频散函数和体波广义反射系数的计算. 地球物理学报 , 1982, 25(2): 130–139. Li Y M, Shu P Y. On surface wave dispersion and body wave generalized reflection coefficient computations for layered media. Chinese J. Geophys. (Acta Geophysica Sinica) (in Chinese) , 1982, 25(2): 130-139. |
| [10] | Chen X F. A systematic and efficient method of computing normal modes for multilayered half-space. Geophys. J. Int. , 1993, 115(2): 391-409. DOI:10.1111/gji.1993.115.issue-2 |
| [11] | Pei D H, John N L, Pullammanappallil S K. Improvements on computation of phase velocities of Rayleigh waves based on the generalized R/T coefficient method. Bull. Seism. Soc. Am. , 2008, 98(1): 280-287. DOI:10.1785/0120070057 |
| [12] | 何耀锋, 陈蔚天, 陈晓非. 利用广义反射-透射系数方法求解含低速层水平层状介质模型中面波频散曲线问题. 地球物理学报 , 2006, 49(4): 1074–1081. He Y F, Chen W T, Chen X F. Normal mode computation by the generalized reflection-transmission coefficient method in planar layered half space. Chinese J. Geophys. (in Chinese) , 2006, 49(4): 1074-1081. |
| [13] | 黄嘉正, 周鸿秋, 关小平. 工程地质中瑞利波法勘探的理论初探. 物探与化探 , 1991, 15(4): 268–277. Huang J Z, Zhou H Q, Guan X P. Theoretical study of the Rayleigh-wave technique in Engineering Geology. Geophysical and Geochemical Exploration (in Chinese) , 1991, 15(4): 268-277. |
| [14] | 张碧星, 肖伯勋, 杨文杰, 等. 瑞利波勘探中"之"形频散曲线 的形成机理及反演研究. 地球物理学报 , 2000, 43(4): 558–567. Zhang B X, Xiao B X, Yang W J, et al. Mechanism of zigzag dispersion curves in Rayleigh exploration and its inversion study. Chinese J. Geophys. (in Chinese) , 2000, 43(4): 558-567. |
| [15] | 张碧星, 鲁来玉, 鲍光淑. 瑞利波勘探中"之"字形频散曲线研究. 地球物理学报 , 2002, 45(2): 263–274. Zhang B X, Lu L Y, Bao G S. A study on zigzag dispersion curves in Rayleigh wave exploration. Chinese J. Geophys. (in Chinese) , 2002, 45(2): 263-274. |
| [16] | Forbriger T. Inversion of shallow-seismic wavefields: I. Wavefield transformation. Geophys. J. Int. , 2003, 153(3): 719-734. DOI:10.1046/j.1365-246X.2003.01929.x |
| [17] | Forbriger T. Inversion of shallow-seismic wavefields: II. Inferring subsurface properties from wavefield transforms. Geophys. J. Int. , 2003, 153(3): 735-752. DOI:10.1046/j.1365-246X.2003.01985.x |
| [18] | Lu L Y, Wang C H, Zhang B X. Inversion of multimode Rayleigh waves in the presence of a low-velocity layer: numerical and laboratory study. Geophys. J. Int. , 2007, 168(3): 1235-1246. DOI:10.1111/gji.2007.168.issue-3 |
| [19] | Zhang B X, Yu M, Lan C Q, et al. Elastic wave and excitation mechanism of surface waves in multilayered media. J. Acoust. Soc. Am. , 1996, 100(6): 3527-3538. DOI:10.1121/1.417329 |
| [20] | Xia J H, Miller R D, Xu Y X. Data-resolution matrix and model-resolution matrix for Rayleigh-wave inversion using a damped least-squares method. Pure Appl. Geophys. , 2008, 165(7): 1227-1248. DOI:10.1007/s00024-008-0364-2 |
| [21] | Xia J H, Miller R D, Park C B. Estimation of near-surface shear wave velocity by inversion of Rayleigh wave. Geophysics , 1999, 64(3): 691-700. DOI:10.1190/1.1444578 |
| [22] | Xu Y X, Xia J H, Miller R D. Approximation to cutoffs of higher modes of Rayleigh waves for a layered earth model. Pure Appl. Geophys. , 2009, 166(3): 339-351. DOI:10.1007/s00024-008-0443-4 |
| [23] | 刘雪明. 瑞雷波地基检测中震源及"之"字形频散曲线的数值研究. 广东: 哈尔滨工业大学城市与土木学科部, 2008. Liu X M. Numerical research on source and zigzag dispersion curve in Rayleigh wave soil exploration . Guangdong: Department of Urban Planning and Civil Engineering,Harbin Institute of Technology, 2008 |
| [24] | 刘江平, 罗银河, 何伟兵. 相邻道瞬态瑞雷面波法与压实度检测. 岩土工程学报 , 2009, 31(11): 1652–1659. Liu J P, Luo Y H, He W B. Method of neighboring trace transient Rayleigh wave and its application in compactness inspection. Chinese Journal of Geotechnical Engineering (in Chinese) , 2009, 31(11): 1652-1659. |
 2011, Vol. 54
2011, Vol. 54