2. 长安大学应用地球物理研究所,西安 710054
2. Institute of Applied Geophysics, Chang'an University, Xi'an 710054 , China
随着生产实践对勘探精度要求的进一步提高,在地震波偏移处理中需要考虑岩石的各向异性.但是,基于各向异性弹性波方程的偏移处理耗时较大,用声波方程来代替弹性波方程进行偏移处理是减小计算量的有效方法之一.因此,自从Alkhalifah(2000)[1]采用声学近似(即令垂向横波速度为零)的办法推导出VTI(具有垂直对称轴的横向各向同性)介质声波方程以来,有关VTI以及TTI(具有倾斜对称轴的横向各向同性)介质声波方程的正演模拟以及偏移成像受到了较广泛的讨论.Klie和Toro(2001)[2]推导了一个近似的VTI介质声波方程.Zhang等(2003)[3]把Alkhalifah[1]提出的声波方程从VTI介质扩展到了TTI介质.Du等(2005)[4]讨论了TTI介质的声波方程伪谱法逆时偏移.Zhou等(2006)[5]把Zhang等[3]的声波方程分成两个耦合的二阶偏微分方程.吴国忱和梁锴(2005,2007)[6, 7]在空间频率域求解VTI 介质声波方程.Fletcher 等(2008)[8]建立了一个更容易求解的VTI介质声波方程.Hestholm (2009)[9] 把Alkhalifah[1] 提出的 VTI介质声波方程转变为一个新的一阶偏微分方程,并利用高阶交错网格有限差分方法求解.Fletcher等(2009)[10]推导了一个新的TTI介质声波方程,并讨论其隐式有限差分求解及逆时偏移.Shan(2009)[11]在Alkhalifah[1]工作的基础上,讨论了VTI介质优化隐式及Fourier 有限差分偏移.Tessmer(2010)[12]讨论了TTI介质声波方程逆时偏移中的不稳定问题.Liu 和Sen(2010)[13]把基于频散关系的正演模拟方法扩展应用于VTI介质声波方程等.
然而,对各向异性介质通过简单地令垂向横波速度为零得到的声波方程并不是一个纯的准纵波(qP波)方程,除了qP波解以外,该方程还包含另一个解[1],该解在波场快照中表现为diamond-shape波形,Grechka(2004)[14]指出该解为准横波(qSV波)解.在正演模拟和偏移处理中,这个横波解带来的问题不仅仅是噪音干扰,而且还会给方程的数值解法额外地增加一个相应的稳定性条件,并且还存在因横波传播速度相对较低而可能具有的较大频散误差.对此横波解干扰问题,虽然Alkhalifah[1]提出了把震源附近区域介质改为各向同性介质的处理方法,但是,这个方法一方面改变了介质的参数,另一方面难以处理由各种散射源所产生的横波,在应用上具有很大的局限性.因此,Klie和Toro[3]在空间-频率域用一种近似方法推导出一个适用于任意各向异性强度的纯qP波方程;Du等[5]采用Taylor级数展开的方法,推导了一个TTI介质纯qP波方程.
本文采用另一种近似方法推导出一个VTI介质纯qP 波方程.我们从精确的VTI介质相速度表达式出发,用待定系数法简化其中的根号项,得到一个近似相速度公式,然后采用误差定量计算来说明该公式的近似程度.接着,由此近似相速度公式通过应用反Fourier变换推导出一个时间二阶、空间四阶声波方程.最后用有限差分数值模拟计算来说明该方程是一个纯的qP 波方程,其数值模拟结果没有横波,并给出一个单炮地震数据算例.
2 相速度的近似本节讨论二维VTI介质相速度的一个新近似公式.
根据Tsvankin(1996)[15]的讨论,二维VTI介质的精确qP波相速度Vp 由(1)式确定
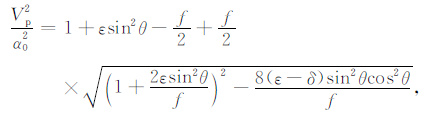
|
(1) |
其中ε和δ 为Thomsen参数[16],θ 为相角,f= (1-β02/α02),α0 和β0 分别为垂向qP 和qSV 波相速度.令垂向qSV 波速度β0 为零,即做声学近似[1],可得
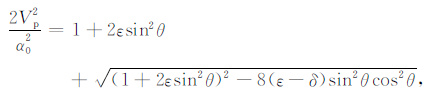
|
(2) |
为简便,记

|
(3) |

|
(4) |
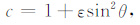
|
(5) |
则(1)和(2)式可分别写成
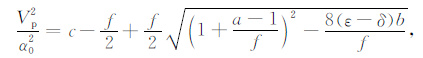
|
(6) |
以及
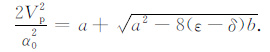
|
(7) |
为了从(7)式推导出声波方程,需要把其中的根号去掉.通常采取的办法是把(7)式的根号项移到等号的一边后再对方程两边取平方运算.例如,Alkhalifah(2000)[1]的VTI介质声波方程、Zhang等(2003)[3]和Zhou等(2006)[5]的TTI介质声波方程,都是基于(7)式通过两边取平方运算去掉根号以后推导出来的.由于对方程两边取平方运算会给(7)式中的相速度Vp 多出新解,这是他们推导出的声波方程除了qP波解以外还有其他干扰解的原因.
为了能推导出一个纯qP 波方程,我们寻找一个关于a和b的多项式来近似(7)式中的根号项.注意到该根号内的表达式具有两项平方差的形式,且为了保持该表达式关于相角θ 的周期性,我们猜测有一个实数e使得(8)式成立
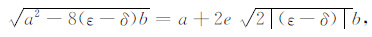
|
(8) |
下面的关键是如何确定实数e的值.
若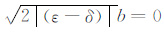
若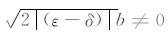
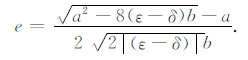
|
(9) |
根据(3)、(4)和(9)式,可知e是Thomsen 参数ε和δ 以及相角θ 的函数.对给定的VTI介质,空间中任意一点的Thomsen参数ε 和δ 是已知的,此时e仅仅是相角θ 的函数.为了下一步能推导出声波方程,e的值须独立于θ.为此,我们再寻找一个与相角θ 无关的常数ec 来近似变量e.注意到e关于θ是一个以2π 为周期的函数,我们用e在一个周期内的平均值珋e来作为e的近似,即取

|
(10) |
其中N为整数,0≤θi≤2π.把(10)式中的ec 当作e代入(8)式,可得
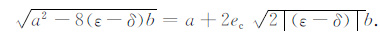
|
(11) |
然而,这样选取的ec 值不一定是最准确的.为了取得更好的近似,我们在此ec 值附近做“微调处理",即在包含当前取值的一个区间上不断改变ec 的值,最后选取一个使得(11)式等号两边数值的差最小的ec 值.这可以通过以下扫描方法来实现:在区间[ec-d,ec+d](d>0)上等间距地取N个数值ei(i=1,2,3,…,N;N为整数),分别计算各数值ei相应的(11)式等号两边数值的差,取该差值最小者所对应的数值ei作为最后的ec 取值.
一旦ec 的值确定了,把(11)式代入(7)式,可得
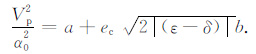
|
(12) |
(12) 式就是本节要寻找的二维VTI介质相速度近似公式.由该式可以较容易地推导出二维VTI介质声波方程.注意,在以上推导过程中,我们没有给相速度Vp 引入新解,这是下一节由(12)式推导出的声波方程没有其他干扰解(如准横波解)的原因所在.
3 二维VTI介质声波方程的推导本节讨论如何从(12)式出发推导出二维VTI介质声波方程.
把(3)和(4)式代入(12)式,有
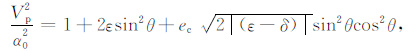
|
(13) |
移项得
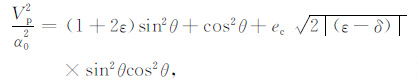
|
(14) |
为简便,令

|
(15) |
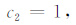
|
(16) |

|
(17) |
则(14)式变为
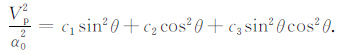
|
(18) |
记kx和kz分别为x和z坐标轴方向的波数,ω 为角频率.利用以下两个平面波关系式
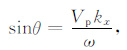
|
(19) |
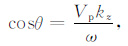
|
(20) |
(18) 式可写为
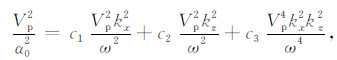
|
(21) |
从(21)式消去Vp2 并进一步化简,可得
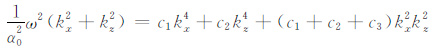
|
(22) |
记P(kx,kz,ω)为频率-波数域波场函数,其相应的时间-空间域形式为p(x,z,t).对(22)式两边同乘P(kx,kz,ω),得到
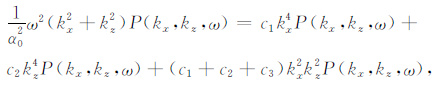
|
(23) |
对(23)式应用反Fourier变换,可得时-空域VTI介质声波方程
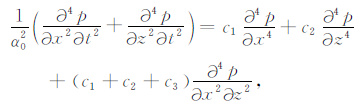
|
(24) |
为了方便求解,引入辅助函数
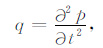
|
(25) |
则(24)式可写成
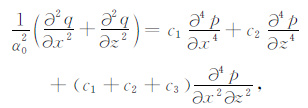
|
(26) |
其中,c1、c2和c3 见(15)~(17)式.(25)和(26)式就是最后得到的VTI介质声波方程.因为在以上推导过程中,我们没有给相速度Vp引入新解,所以该方程没有横波解,是纯的qP方程.
同时由第2 节的推导可知,ec 的值与介质的 Thomsen参数ε和δ 有关.但是,在给定介质参数以后,ec 在各空间点上的值可预先算出,然后由(15)~(17)式即可计算出声波方程(25)和(26)式的所有系数,ec 值的计算不会在后面的数值模拟和偏移处理中占用CPU 时间.
4 数值算例 4.1 相速度误差的计算和分析由第2节可知,二维TTI介质的精确qP 波相速度Vp 可由(6)式确定.因为相速度值Vp 和α0 都是正的,所以(6)式等号右边的值应该大于零,即(6)式隐含有以下条件:
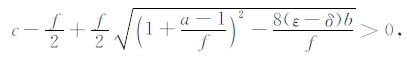
|
(27) |
在这个条件下,由(6)式可以解得二维TTI介质精确相速度Vp 的表达式:

|
(28) |
同样地,(12)式隐含有以下条件:
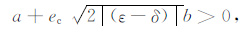
|
(29) |
在这个条件下,可以解得本文推导的二维TTI介质近似相速度Vp 的表达式:
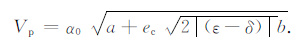
|
(30) |
利用(28)和(30)式可以对精确和近似相速度进行定量计算.下面给定几组VTI介质参数值,通过比较(28)和(30)式计算结果的偏差来说明本文所提出相速度表达式的近似程度.
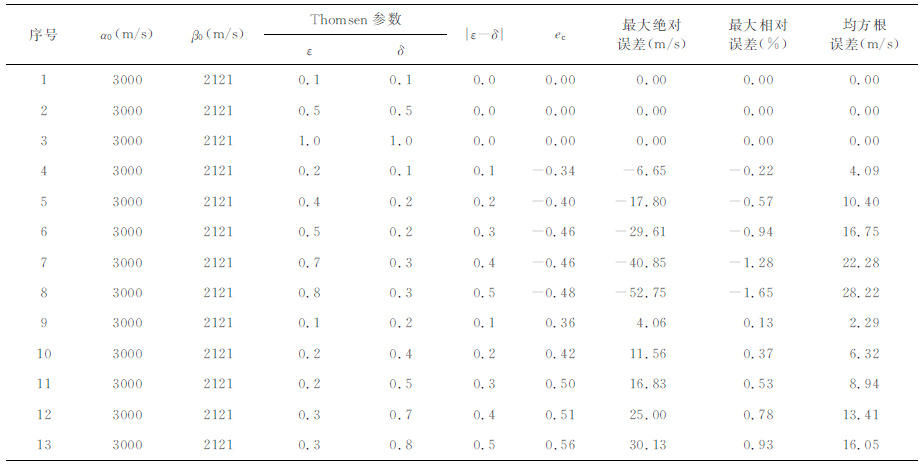
容易验证,(28)和(30)式所表示的相速度Vp关于相角θ 都是以2π为周期的函数.因此我们只须在一个周期内统计相速度Vp 的误差,所得结果见表 1.表 1中共有13组VTI介质参数,各组参数的垂向qP 和qSV 波速度α0 和β0 都是一样的,α0 和β0 分别取为3000 m/s和2121 m/s.表 1 中各组参数的ec 值按本文第2节给出的方法确定.
|
|
表 1 近似公式相速度误差统计表 Table 1 Phase velocity errors for the approximate formula |
表 1中第1~3组数据的ε 和δ 值相等,但取值依次增大,分别为0.1、0.5和1.0,所对应介质的各向异性强度依次增强.从表 1可见,这三组参数的最大绝对误差、最大相对误差和均方根误差都为零.此外,若将ε=δ 代入(28)式,联合(4)和(5)式,化简可得精确相速度表达式:
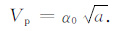
|
(31) |
同样地,把ε=δ代入(30)式,可得近似相速度表达式:
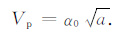
|
(32) |
(31) 和(32)式是一样的,这说明当ε=δ 时,不管介质各向异性的强弱如何,本文提出的相速度公式都是精确的.这在理论上说明了表 1中第1~3组参数近似公式的相速度误差为零的原因.
表 1中其余10组(第4~13组)参数是ε≠δ 的情况.前5组(即第4~8组)参数ε>δ,ε和δ 之差的绝对值|ε-δ|(下面简称“差值")逐渐增大.从表 1的误差数据可以看出,当ε>δ 时,随着ε和δ 差值的增大,这5组参数的各种误差也逐渐增大,误差最大的是第8组,其最大绝对误差、最大相对误差和均方根误差分别为-52.75m/s、-1.65%和28.22m/s.后5组(即第9~13组)参数ε<δ,ε和δ 的差值也逐渐增大.从表 1的误差数据可以看出,当ε<δ 时,随着ε和δ 差值的增大,这5 组参数的各种误差也是逐渐增大的,误差最大的是第13 组,其最大绝对误差、最大相对误差和均方根误差分别为30.13m/s、0.93%和16.05m/s.
表 1中第4~13组参数的误差统计说明,当ε≠δ时,本文所提出相速度公式的误差随ε 和δ 差值的增大逐渐增大.
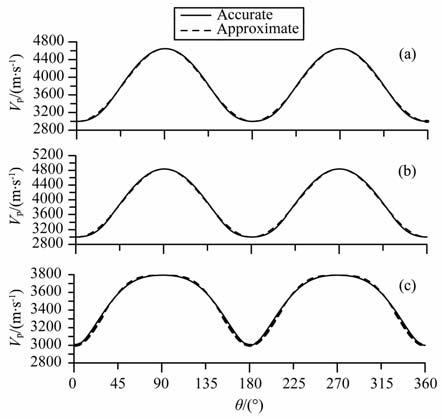
为说明近似相速度误差在一个周期上的分布情况,下面把表 1中误差最大的第7、8和13组参数相应的近似和精确相速度曲线绘出,分别见图 1a、图 1b和图 1c.图 1的曲线说明相速度误差在整体上分布较为均匀,没有在某个相角附近出现误差明显较大的现象,其原因与我们在做相速度近似时采用了最小均方差准则有关.
|
图 1 精确和近似相速度曲线的对比 (a)ε=0.7,δ=0.3;(b)ε=0.8,δ=0.3;(c)ε=0.3,δ=0.8. Fig. 1 Comparison between accurate and approximate phase velocity curves |
本小节计算、对比和分析本文所提出VTI介质声波方程和前人方程的有限差分数值模拟波场快照,旨在说明本文的VTI声波方程模拟所得qP 波在运动学特征(波前形态)上的近似程度以及该声波方程是否为纯qP波方程.
共对两个VTI介质模型进行计算,介质的参数分别采用表 1中误差最大的第8组以及误差最小的第3组参数,两组参数分别对应ε≠δ 和ε=δ 的情况.对每组介质参数,都分别采用本文的VTI介质声波方程、文献[1]的经典VTI介质声波方程和 VTI介质弹性波方程进行有限差分数值模拟计算.图 2和图 3分别绘制了这两组介质参数的三个波动方程数值模拟波场快照.
根据图 2和图 3,我们首先分析qP 波波前的精度.对比可见,图 2和图 3中各小图qP 波波前的几何形态基本一致.这说明本文以及文献[1]的声波方程所模拟得到的qP 波在运动学特征上与未做声学近似的弹性波方程都较为接近.

|
图 2 波场快照对比(ε=0.8,δ=0.3) (a)弹性波方程;(b)本文的声波方程;(c)文献[1]的声波方程. Fig. 2 Comparison of snap shots with ε=0.8 and δ=0. (a) Elastic wave equation; (b) Acoustic wave equation presented here; (c) Acoustic wave equation from Ref.[1]. |
其次分析各方程的模拟结果是否存在qSV 波.对比可见,图 2b 和图 3b 都没有qSV 波,这说明本文的VTI介质声波方程是一个纯qP 波方程.此外还可见,图 3c没有qSV 波,而图 2c有qSV 波,这说明文献[1]的VTI介质声波方程在ε=δ 时也可以实现纯qP波波场模拟,但在ε≠δ时其模拟所得的波场中除了qP波以外,还有qSV 波,即其不是一个纯qP波方程.
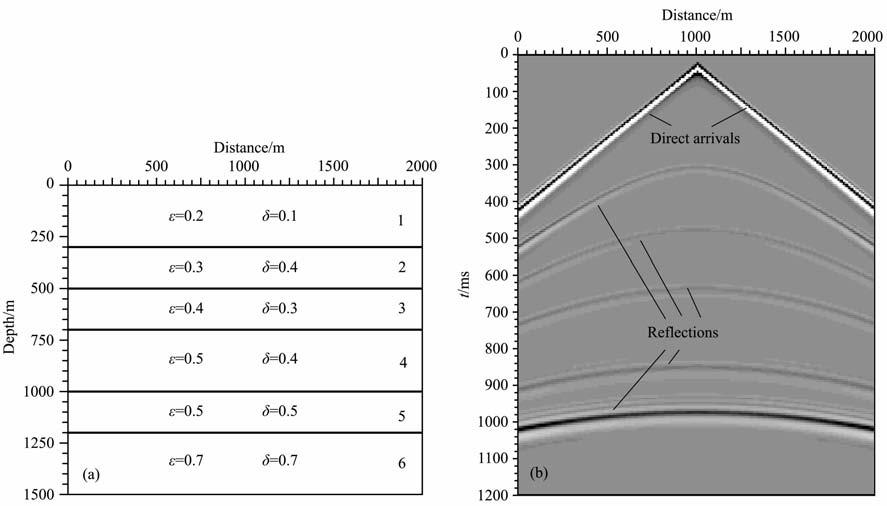
4.3 数值模拟地震记录为说明本文所推导VTI介质声波方程在数值模拟上的可行性,采用一个6层水平层状VTI介质模型进行有限差分数值模拟计算.模型各地层的垂向纵波速度从上到下分别为2100、2300、2500、2800、3250和5050m/s, 各层的Thomsen参数ε 和δ 值见图 4a.其中,第1、3和4层ε 大于δ,第2层ε小于δ,第5和第6层ε 等于δ.图 4b是采用本文的 VTI介质声波方程计算得到的中间激发、两边接收单炮地震记录.记录的激发点坐标为(1000,0),第一和最后一个接收点的坐标分别为(0,0)和(2000,0),道间距为10m, 共有201个接收点.
|
图 4 VTI介质模型(a)及数值模拟单炮地震记录(b) Fig. 4 VTI media model (a) and a numerical modeling seismic single-shot record (b) |
从图 4b可以看到出现时间较早的直线形直达波同相轴,以及后续的5 个速度界面的类双曲线形反射波同相轴,且这些双曲线互不交叉.这些运动学特征与各向同性声波方程合成记录类似,说明本文推导的VTI介质声波在数值正演模拟以及波场外推上是稳定、可行的.
5 结论声学近似是简化各向异性介质地震数据处理的有效方法之一,而包含有横波噪音的声波方程一方面会影响处理效果,另一方面还会给方程的数值求解增加更严格的稳定性条件.因此,推导纯纵波的各向异性介质声波方程是相关研究及工作人员探索的一个方向.本文按照最小均方差准则,利用一种搜索的方法取得相速度的高精度近似,从而推导出了一个VTI介质声波方程,其模拟的波场中没有准横波.误差统计和地震波数值模拟结果说明了该方程的精度和求解的稳定性.在Thomsen参数ε 和δ 差相等或相差不大时,可以利用该声波方程较精确地进行准纵波数值模拟和偏移处理;当ε 和δ 的差较大时,也可用该声波方程进行各种处理得到近似结果,或者将其用于迭代反演和偏移处理的中间步骤.
致谢感谢审稿专家和编辑所给予的十分有用的建议.
| [1] | Alkhalifah T. An acoustic wave equation for anisotropic media. Geophysics , 2000, 65(4): 1239-1250. DOI:10.1190/1.1444815 |
| [2] | Klíe H, Toro W. A new acoustic wave equation for modeling in anisotropic media. SEG Expanded Abstracts , 2001: 1171-1174. |
| [3] | Zhang L, Rector J W, Hoversten G M. An acoustic wave equation for modeling in tilted TI media. SEG Expanded Abstracts , 2003: 153-156. |
| [4] | Du X, Bancroft J C, Lines L R. Reverse-time migration for tilted TI media. SEG Expanded Abstracts , 2005: 1930-1933. |
| [5] | Zhou H B, Zhang G Q, Bloor R. An anisotropic acoustic wave equation for modeling and migration in 2D TTI media. SEG Expanded Abstracts , 2006: 194-198. |
| [6] | 吴国忱, 梁锴. VTI 介质频率-空间域准P波正演模拟. 石油地球物理勘探 , 2005, 40(5): 535–545. Wu G C, Liang K. Quasi P-wave forward modeling in frequency-space domain in VTI media. Oil Geophysical Prospecting (in Chinese) , 2005, 40(5): 535-545. |
| [7] | 吴国忱, 梁锴. VTI介质qP波方程高精度有限差分算子. 地球物理学进展 , 2007, 22(3): 896–904. Wu G C, Liang K. High precision finite difference operators for qP wave equation in VTI media. Progress in Geophysics (in Chinese) , 2007, 22(3): 896-904. |
| [8] | Fletcher R P, Du X, Fowler P J. A new pseudo-acoustic wave equation for TI media. SEG Expanded Abstracts , 2008: 2082-2086. |
| [9] | Hestholm S. Acoustic VTI modeling using high-order finite differences. Geophysics , 2009, 74(5): T67-T73. DOI:10.1190/1.3157242 |
| [10] | Fletcher R P, Du X, Fowler P J. Reverse time migration in tilted transversely isotropic (TTI) media. Geophysics , 2009, 74(6): WCA179-WCA187. DOI:10.1190/1.3269902 |
| [11] | Shan G J. Optimized implicit finite-difference and Fourier finite-difference migration for VTI media. Geophysics , 2009, 74(6): WCA189-WCA197. DOI:10.1190/1.3202306 |
| [12] | Tessmer E. Reverse-time migration in TTI media. SEG Expanded Abstracts , 2010: 3193-3197. |
| [13] | Liu Y, Sen M K. Acoustic VTI modeling with a time-space domain dispersion-relation-based finite-difference scheme. Geophysics , 2010, 75(3): A11-A17. DOI:10.1190/1.3374477 |
| [14] | Grechka V, Zhang L B, Rector J W III. Shear waves in acoustic anisotropic media. Geophysics , 2004, 69(2): 576-582. DOI:10.1190/1.1707077 |
| [15] | Tsvankin I. P-wave signatures and notation for transversely isotropic media: An overview. Geophysics , 1996, 61(2): 467-483. DOI:10.1190/1.1443974 |
| [16] | Thomsen L. Weak elastic anisotropy. Geophysics , 1986, 51(10): 1954-1966. DOI:10.1190/1.1442051 |
 2011, Vol. 54
2011, Vol. 54