随着勘探难度的增加，对地震勘探技术提出了更多的挑战，要求实现精细的油藏描述.提高油藏定量描述精度是提高油气勘探开发效益的核心，引入更多的地震信息并提高地震反演的精度是实现油藏定量描述的关键.地震数据本质上讲是非垂直入射的，但在实际应用中常简化为垂直入射，损失了隐藏在地震道集中的AVO 信息；叠前地震反演本质是非线性的，但目前多采用线性方法近似求解，降低了地震反演的精度.因此，要提高油藏描述的能力就应该从叠后走向叠前，从线性向非线性延伸^[1~3].

AVO 分析方法是利用“地震反射振幅随炮检距变化"特征进行岩性、物性和流体特征分析的技术，其理论基础是Zoeppritz方程^[4]，它精确表示了振幅随入射角变化与岩性参数之间的复杂关系，但难以给出清楚的物理概念，这种数学上的复杂性和物理上的非直观性一度延缓了Zoeppritz方程的实际应用.1955年，Koefoed^[5]提出反射系数随入射角变化的曲线形态具有分析岩性的潜力，然而由于水平叠加技术对地震数据信噪比的改善取得了巨大的成功，人们对地震信息的关注一直停留在叠后数据上.直到20世纪80年代，Ostrander^[6]计算了不同弹性模型的AVO 响应，提出“含气砂岩的反射振幅随炮检距增大而增大，含水砂岩的反射振幅随炮检距增大而减小"，并将反射系数随炮检距变化的特点用于亮点型含气砂岩的识别，这使得人们的注意力重新回到了叠前地震数据.为了使Zoeppritz方程更加容易理解，具有较明显的物理意义，不少学者基于不同的假设和目的研究推导了一些近似公式.Bortfeld(1961)^[7]在假定界面两侧弹性参数差异较小的情况下，简化了Zoeppritz方程，并给出了相应的AVO反射系数和透射系数近似解析解，Bortfeld指出，这些近似解析解的精度足以满足反射波地震勘探的需要，并且在一定程度上揭示了影响反射系数和透射系数的主导因素.Hilterman^[8]将对数公式的近似式代入Bortfeld近似公式，整理后得到了新的公式，其第一项只含纵波速度和密度，不含横波速度，显然当法线入射时，其结果为大家熟知的反射系数公式.但是Hilterman近似公式形式仍然比较复杂，物理意义也不够明显.Aki和Richards(1980)^[9]在假定界面两侧相对纵波速度差异、相对横波速度差异和相对密度差异远小于1 的情况下，给出了以相对纵波速度差异、相对横波速度差异、相对密度差异和纵横波速度比为参量的AVO 近似公式.Shuey(1985)^[10]对Aki-Richards公式进行了适当的修改，给出了以泊松比为变量的近似公式，揭示了介质两侧泊松比的变化对AVO 效应的影响.该公式表明在上下两层介质的波阻抗一定时，泊松比差对反射振幅随入射角的变化影响很大，泊松比差越大振幅随入射角的变化也越大.在一定条件下，当砂岩中充气时，砂岩泊松比明显下降，从而导致上、下介质的泊松比差相应增加.为了避免三参数AVO 反演的不稳定性，Smith和Gidlow(1987)^[11]利用Gardner^[12]公式，从Aki和Richards的公式出发，消去其中的密度项变量，得到了以相对纵波速度差异、相对横波速度差异和纵横波速度比为参量的近似公式，但该公式过于依赖Gardner经验公式.基于相邻两层介质的弹性参数变化较小，郑晓东^{[13， 14]}于1991 年提出了基于奇偶幂级数形式的近似公式，给出了完整的反射、透射表达式，并将转换波和非转换波的振幅系数分别表示成幂级数的奇、偶次项之和.为了避免 Smith-Gidlow 近似公式过多依赖于Gardner经验公式，Fatti(1994)^[15]用权叠加方法得到了纵波阻抗、横波阻抗的相对差异，并用于气层的检测.Verm(1995)^[16]重新整理了Shuey公式，突出了岩石特性对入射角的依赖关系，整理后可看出近角度响应主要受声阻抗变化的影响，中角度响应受泊松比变化的影响，而远角度响应受纵波速度变化的影响.Smith(1996)^[17]提出了基于权叠加的三参数反演的思路.Goodway^[18]于1997 年给出了用拉梅常数和密度表示的反射系数近似公式.Gray(2002)^[19]给出了利用体积模量、剪切模量和密度以及用拉梅常数和密度的相对变化量表示的近似公式，这些弹性参数可以分别用于储层岩性和流体的描述.Ursenbach(2004)^[20]，Downton(2004)^[21]等一批学者尝试着用非线性和全波形的方法进行三参数反演.总之，AVO 反演方法目前仍主要使用线性近似方法，对于非线性三参数AVO 反演方法还处于探索阶段.

在AVO 反演中，最常用的是Aki-Richard公式:

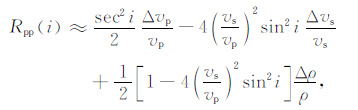
(1)

其中，R_pp 为纵波反射系数，i为入射角度，v_p, v_s, ρ分别为纵波速度、横波速度和密度，Δv_p/v_p, Δv_s/v_s, Δρ/ρ 分别为纵波速度、横波速度和密度的相对变化量.为了求解便利，通常假定v_s/v_p 为常量(工业界常取0.5)，把式(1)转化为线性近似公式:

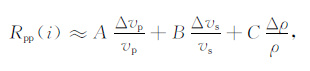
(2)

其中:A=0.5sec²i，B=-sin²i，C=0.5cos²i，给定角度i，A、B和C是常量，利用式(2)以参数的相对变化量为反演变量进行反演，线性近似影响了 AVO 参数反演的精度和结果的可靠性.在本研究中，我们不再把v_s/v_p 看作常量对公式进行线性近似，直接以v_p, v_s, ρ 作为反演变量，根据式(1)的 Aki-Richards公式采用量子蒙特卡罗方法^{[22， 23]}进行非线性反演.量子蒙特卡罗反演方法的具体原理和实际模拟过程参见文献[24~26]，在此不再赘述.

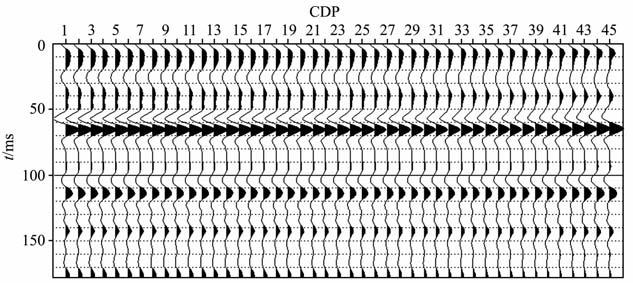
下面利用A 地区某一口井的纵波速度、横波速度和密度生成叠前角道集(如图 1所示)后进行反演加以说明.具体的反演步骤如下:

图 1

Fig. 1

图 1 A地区某井资料合成的叠前角道集 Fig. 1 The pre-stack angle gather generated by using of logging data in area A

(1) 从叠前数据抽取近角度、中角度和远角度叠加地震数据，并提取近角、中角和远角子波；

(2) 以层位为约束，利用井资料建立低频模型作为初始模型；

(3) 针对不同的角度数据，以式(1)或式(2)计算不同角度的纵波反射系数，并和子波褶积得到模型数据d₀，以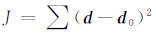为目标函数(d为实际数据)；

(4) 以量子蒙特卡罗反演方法进行反演，通过逐步迭代使目标函数J趋于最小化.

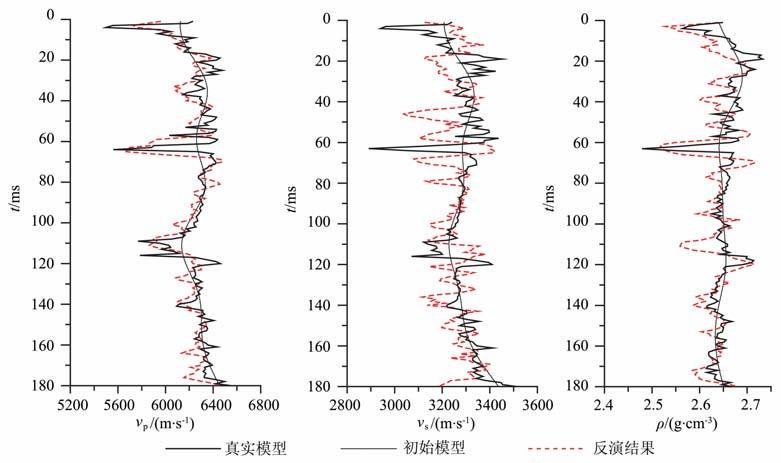
图 2是利用式(2)进行线性近似反演的结果，纵波速度反演结果最好，也最稳定，密度次之，横波速度的结果最差.图 3是直接使用式(1)进行非线性反演的结果，虽然横波速度反演精度相对于线性反演有提高，仍然存在较大的误差.

图 2

Fig. 2

图 2 AVO线性近似反演结果 Fig. 2 AVO linear inversion results

图 3

Fig. 3

图 3 AVO非线性反演结果 Fig. 3 AVO non-linear inversion results

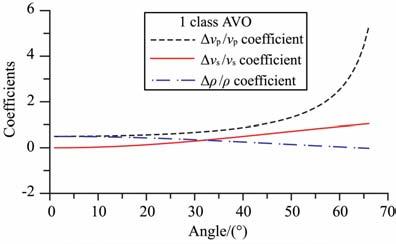
图 3的非线性反演结果较之于线性反演结果有了一定的改善，但还存在较大误差，而且两次反演各参数误差大小相似，横波速度误差最大，密度误差次之，纵波速度误差相对最小.下面基于式(1)的Aki- Richards公式，对影响v_p, v_s, ρ 反演精度的原因进行分析.Aki-Richards公式中，v_p, v_s, ρ 都是以相对变化量(Δv_p/v_p, Δv_s/v_s, Δρ/ρ)和v_s/v_p 的形式表示，差别仅在于各相对变化量的系数存在差异，那么这种差异是否就是导致上述两次反演中参数误差大小不一的原因所在呢?我们比较了四类AVO 模型的系数，结果基本类似，图 4是Ⅰ类AVO 模型相对变化量的系数项大小的比较，可以看出，在有效的角度内，Δv_p/v_p 的系数一直是比较稳定的，随入射角变化相对较小，Δρ/ρ 的系数在近角度内比较接近Δv_p/v_p 的系数，但是随着角度的增大在逐渐变小，而Δv_s/v_s的系数变化不大，但和Δv_p/v_p 系数相比差了两个数量级.由于各系数之间这种极大的不均衡，导致方程的求解存在奇异性，直接影响了各参数反演的精度，纵波v_p 精度最高，密度ρ 精度次之，横波v_s 精度最低，这是由于它的相对变化量Δv_s/v_s 的系数在有效角度内太小，反演中横波的变化所能引起的反射系数的变化非常小，进而反演结果也就偏差很大.这说明，各参数的反演精度和其相对变化量系数的大小有着直接的对应关系.

图 4

Fig. 4

图 4 Aki-Richards近似公式vp, vs, ρ相相对变化量系数项比较 Fig. 4 The comparison of compressional velocity, shear velocity and density coefficient of Aki-Richards approximate formula

针对上述分析，本文提出了反向加权AVO 反演方法.反演中，并没有对Aki-Richards公式本身做任何改变，只是针对不同参数的反演，给它增加一个反向权重系数C_x：

(3)

其中，C_x分别为C_vp，C_vs，C_ρ，其大小和各参数相对变化量系数项的大小成反向关系：

(4)

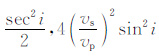
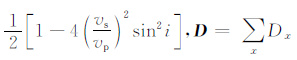
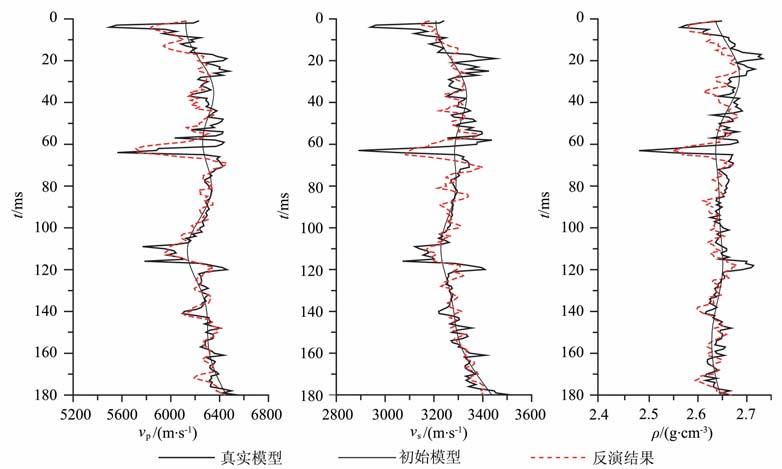
其中，D_x分别为各参数系数项, 表示各参数系数项求和，λ_x为各参数调控因子，0~1之间取值.通过这种反向加权，对各系数项进行了适当均衡，也均衡了各系数项引起的反射系数的响应差异，降低了各系数不均衡导致的方程求解的奇异性，改善了横波速度和密度的响应敏感度.图 5 是前例的反向加权的反演结果，和图 2、图 3 反演结果相比可以看出，横波速度和密度的反演结果有了很大的改善，整体提高了反演的精度.图 6是线性近似反演、非线性反演和反向加权非线性反演的相对误差的比较(相对误差).纵波速度的非线性反演和线性近似反演的相对误差相当，均在5%左右，其反向加权非线性反演相对误差则下降到3% 左右；密度的非线性反演和线性近似反演的相对误差也都基本接近2%，其反向加权非线性反演相对误差则不足1%；横波速度的反演精度变化最大，其线性近似反演相对误差超过16%，非线性反演相对误差降低至14%左右，而反向加权非线性反演相对误差则降至4%左右.总的来说，纵波速度、横波速度和密度的反向加权非线性反演相对误差较之于线性近似反演和非线性反演的相对误差有了很大幅度的降低，明显提高了反演结果的精度.

图 5

Fig. 5

图 5 AVO反向加权非线性反演结果 Fig. 5 Reverse weighted AVO non-linear inversion results

图 6

Fig. 6

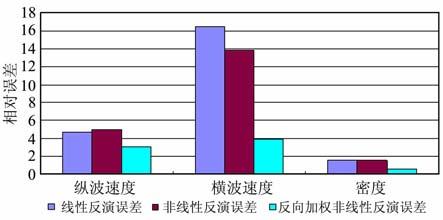
图 6 不同AVO反演方法相对误差比较 Fig. 6 The comparison of relative error of dilferent AVO inverse methods

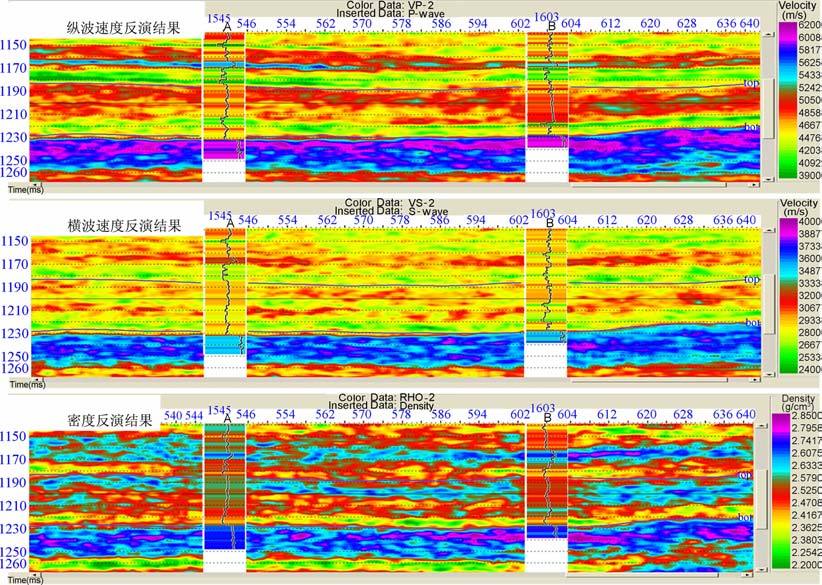
在这一节中，我们利用B 地区某一测线的叠前资料进行了反向加权反演.图 7 是测线的近、中、远角道集，其中共有两口井，A 井是干井，B 井是气、油井.利用两口井的资料建立低频模型作为初始模型进行反演，图 8是反演结果，其与测井对比，有很好的对应性，能够反映出已知井周围v_p, v_s, ρ 的特征及储层的分布情况.将其进一步与钻井结果进行对比，也很好地验证了反演结果的可靠性和有效性.

图 7

Fig. 7

图 7 实际资料的近、中、远道集 Fig. 7 The small, middle and large angle gathers of practical seismic data

图 8

Fig. 8

图 8 实际资料的反向加权反演结果 Fig. 8 The reverse weighted tnverse results of practical seismic data

本文提出了一种反向加权AVO 反演方法，它较之于传统的AVO 反演，不再假定纵横波速度比为常量，可以直接反演得到纵波速度、横波速度和密度.相对于直接的非线性反演方法，它均衡了各参数系数项引起的响应差异，改善了横波速度和密度的响应敏感度，整体提高了反演精度.通过理论模型的计算和实际叠前资料的反演，表明该方法有很好的稳定性和收敛性，可以改善叠前反演的精度，提高储层定量描述的能力.当然，从模型试算的结果看(图 5)，反演结果的细节还有一定的改善空间，这将是今后研究的一个重点.