2. 安徽省地震局工程院,合肥 230031;
3. 甘肃省地震局兰州观象台,兰州 730046;
4. 菲律宾大气和地球物理与空间科学处
2. Academy of Engineering of Anhui Earthquake Bureau, Hefei 230031, China;
3. Lanzhou Observatory of Gansu Earthquake Bureau, Lanzhou 730046, China;
4. Philippine Atmospheric, Geophysical and Astronomical Services Administration(PAGASA), Philippines
地磁场作为地球基本物理场,具有复杂的空间分布和时间演化规律.准确掌握某一地区地磁场的时空分布规律,对地磁场的研究和应用有着重要的意义.区域地磁图作为一个国家(地区)基本的、重要的基础数据,备受重视.许多国家建立了自己的区域地磁图[1~9].我国从1950 年开始编制中国地磁图,并利用它对地磁场各种时空分布特征进行研究[10~18].要想建立时空分布比较精确的地磁图,依赖于精确的地磁场基础测量数据.
菲律宾共和国位于亚洲东南部,西濒南中国海,东临太平洋,是一个群岛国家,共有大小岛屿7107个.陆地面积29.97万km2,其中吕宋岛、棉兰老岛、萨马岛等11 个主要岛屿占全国面积的96%.在此之前,菲律宾地区还从未建立区域地磁图,更没有对区域地磁场做深入的分析和研究.
为了实现菲律宾第一次全国区域地磁图的建立,研究菲律宾地磁分布特征和中国地磁分布的联系,探索菲律宾板块与中国东部块体的相互作用对中国地磁场分布的影响.在2005~2007年期间,中国地震局地球物理研究所(IGPCEA)与菲律宾大气、地球物理与天文服务局(简称PAGASA)在菲律宾境内合作测量了9个点的地磁三分量数据(D、I、F).2001~2005年期间,菲律宾国家绘图和资源局(NAMRIA)在菲律宾境内测量了82点的地磁基本场矢量数据(F、D、H、Z),其中79个测点数据齐全.本文根据这些地磁场实测数据,经过数据处理,最后选用74个实测点数据,用泰勒多项式和球冠谐和两种方法建立了2005.0 菲律宾及周边地区地磁基本场区域模型,分析研究了菲律宾地区地磁场X、Y、Z、D、I、H、F七分量的分布特征.并将模型反映的地磁场的分布与根据第10 代国际地磁参考场模型(The 10th International Geomagnetic Reference Field, 简称IGRF10)计算得到的2005.0 年代菲律宾地区的地磁场分布作了比较.
2 方法和资料 2.1 建模方法地磁场模型的建立方法有多种.本文采用球冠谐和、泰勒多项式两种模型计算方法.
地磁场球冠谐模型计算方法是加拿大学者 HainesG V 于1985 年创建的,用于计算地磁场区域模型.与球谐方法相类似,球冠谐方法从标量磁位展开,对位函数求导可得到地磁场.
矢量分量在限定区域内的表达式:
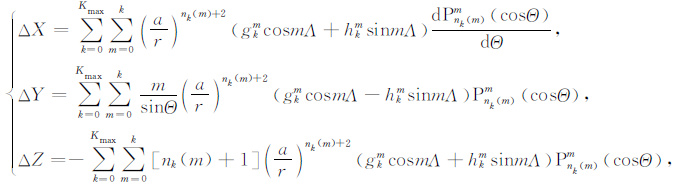
|
(1) |
式中,Λ 和Θ 分别为球冠坐标系中的经度和余纬,a是地球的参考半径(a=6371.2km),r是离开地心的径向距离;Pnk(m)m(cosΘ)是非整数阶nk(m)和整数次m的Schmidt缔合Legendre函数.Kmax 代表球冠谐分析的截断阶数,球冠谐模型共有(Kmax +1)2个系数,球冠谐系数gkm和hkm是根据地磁场的观测值用最小二乘法来确定的.
泰勒多项式是最简单、传统的建立地磁基本场区域模型计算方法.该方法对地磁场矢量在限定区域内的表达式如下:
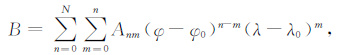
|
(2) |
式中的Anm为泰勒多项式的系数,N为泰勒多项式的截断阶数,φ 和λ 分别为地磁测点的纬度和经度,φ0 和λ0 分别为泰勒多项式展开原点的纬度和经度,单位为rad.B可以表示地磁场不同的分量,如F、D、I等.
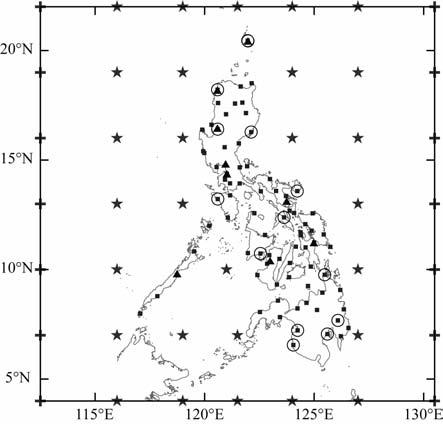
2.2 资料与建模本文研究以2007年中国地震局地球物理研究所与PAGASA 合作测量得到的菲律宾境内9个测点的D、I、F三分量数据和NAMRIA 提供的菲律宾境内2001~2005年期间82个测点的地磁场数据(F、D、H、Z)为最初研究数据,其中由于NAMRIA 提供的82个测点数据中,测点ZAMBOANGA、GENSAN、 BONGAO 缺失总强度的数据,故舍弃了这3 个测点.因此,最终综合选定剩余88个流动测点的资料,及2007年1月菲律宾Muntinlupa地磁台和中国琼州地磁台的数据作为本文研究的基础数据.菲律宾地区88个地磁测点及边界约束点如图 1所示.
|
图 1 测点位置图 ▲中菲合作测量的点,■NAMRIA提供的测点,+仅用于泰勒多项式模型的边界约束点,+★用于球冠谐和模型的边界约束点,○舍去的测点 Fig. 1 Survey sites ▲ByCEAand PAGASA,■ByNAMRIA,+Used inTaylor model, +★Used in spherical cap harmonic model, ○Deleted |
数据处理和建模的主要步骤如下:
首先,在数据处理过程中,为了确保台站数据的可靠性,将2007 年1 月中国海南岛琼州地磁台的D、Z、H绝对观测分钟值数据与Muntinlupa地磁台的观测数据进行对比.确认了Muntinlupa数据质量的不可靠性,因此选择所能得到的离菲律宾最近的琼州地磁台作为通化参考台,对测点数据进行日变改正.然后,依据IGRF10,将F、D、I、H、X、Y、Z七个分量进行长期变改正,通化到2005.0年代.
其次,将上述方法处理得到的X、Y、Z三个分量的数据与IGRF10 计算值对比,对应空间点上的相同分量数值相差大于500nT 时,视为异常点并剔除,共去掉了14个异常点,表 1中给出了这14个点相关信息.剩余74个测点的数据是菲律宾地磁图所使用的测量数据.根据边界效应的空间分布特征,确定了球冠谐和模型的IGRF10约束点为42个,泰勒多项式模型的约束点为28个(如图 1所示).
|
|
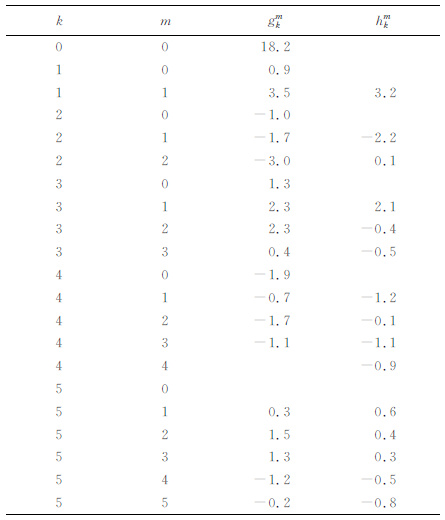
表 1 截断阶数为5阶的球冠谐系数 Table 1 The coefficients of 5-order SCH model |
通过上述数据处理,最终获得了2005.0菲律宾及周边地区地磁基本场测量数据集.
3 结果分析建立球冠谐和、泰勒多项式模型,首先必须确定两种模型的截断阶数.如何确定合适的截断阶数,是区域模型计算的难点,一般根据计算区域的范围、边界效应和均方差综合考虑确定.
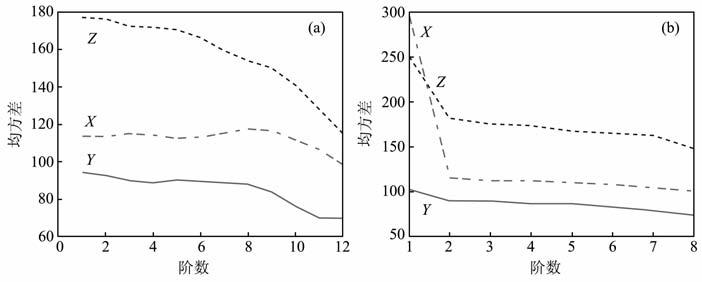
图 2a是根据球冠谐和模型计算的X、Y、Z三分量的均方差,图 2b 是根据泰勒多项式模型计算的X、Y、Z三分量的均方差.从图 2a可以看出,X分量的均方差在5阶附近出现第一个低值;Y分量的均方差在4阶出现第一个低点,在9阶时Y分量出现一个大的拐点;Z分量的均方差直到本文计算的最大阶次12阶时,依然没有出现明显的拐点.从图 2b中看出X、Y、Z三个分量的均方差都在2阶处出现明显的拐点,之后随着阶数的增加,三个分量的均方差基本保持不变.根据图 2a和模型试算知:虽然X、Y、Z三分量的均方差在8~10阶均下降,但是由于截断阶数的增高,使得所建立的菲律宾地区的球冠谐和模型边界效应表现更明显.
|
图 2 根据球冠谐模型(a)和泰勒模型(b)所计算的均方差与阶数的关系 Fig. 2 RMS in Spherical Cap Harmonic and Taylor method |
综合考虑菲律宾地区面积大小、均方差和边界效应的影响,本研究最终确定球冠谐模型的截断阶数为5阶,泰勒模型的截断阶数为3阶.
3.1 球冠谐模型的计算结果以121.5°E,13.0°N为球冠极点,以10°为球半角,以116.0°E~127.0°E、4.0°N~22.0°N 为计算区间.计算得到了菲律宾地区的地磁场球冠谐系数(表 1)及地磁场球冠谐和模型的七分量分布图,如图 3所示.
|
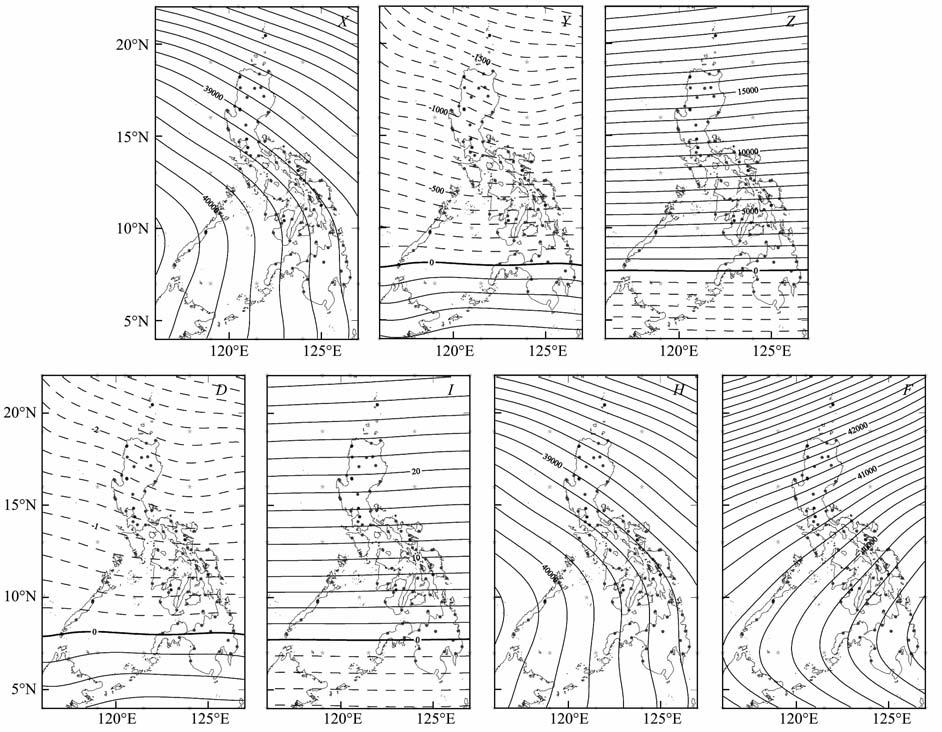
图 3 球冠谐和模型计算的菲律宾地磁场空间分布(D和I的单位为°,X、Y、Z、H、F单位为nT) Fig. 3 The geomagnetic spatial structure in Philippines by SCH (D and I,unit:°,X,Y,Z,H and F,unit:nT) |
图 3可以看出,X、H的分布相似,在10°N 左右出现系统的拐点,使X、H的分布由高纬地区的北西-南东走向转为低纬地区的近似北东-南北走向,这种分布使得同纬度地区的X、H东高西低,最大值均分布在9°N,116°E 左右的地区.D、Y空间分布特征相似,零线分布于8°N 左右呈东西展布,其北侧为负,南侧为正,且等值线沿经度分布的同时,在纬度上有不同程度的小起伏.D值的分布大约在0.5°至-2.5°,Y值的分布大约在500nT至-1700nT.Z、I空间分布呈现比较规则均匀的东西向分布,等值线比D、Y两个分量的等值线更规则、光滑.零线分布在7.5°N 左右,零线北部是正值区域,南部是负值区域,Z、I正的最大值分布在菲律宾的最北端,分别为20000nT 和28°,负的最大值分布在菲律宾的最南端,分别为-600nT 和-5.5°.在10°N 以北地区,总强度F的等值线呈现北东-南西向分布,在8°N左右总强度的等值线出现系统拐点,在10°N 以南地区,总强度的等值线呈现北西-南东向分布,总强度最大值分布在8°N,126°E左右,值约为40800nT.
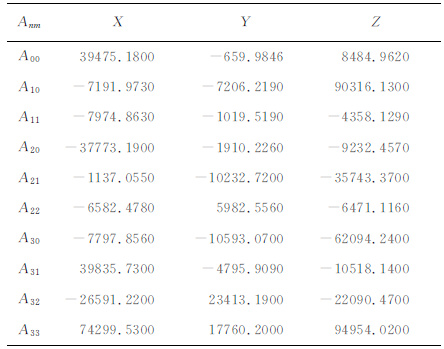
3.2 泰勒模型的计算结果以116.0°E~127.0°E、4.0°N~22.0°N 为计算区间,以3阶截断阶数进行泰勒计算(图 4).表 2给出截断阶数为3阶的泰勒系数.
|
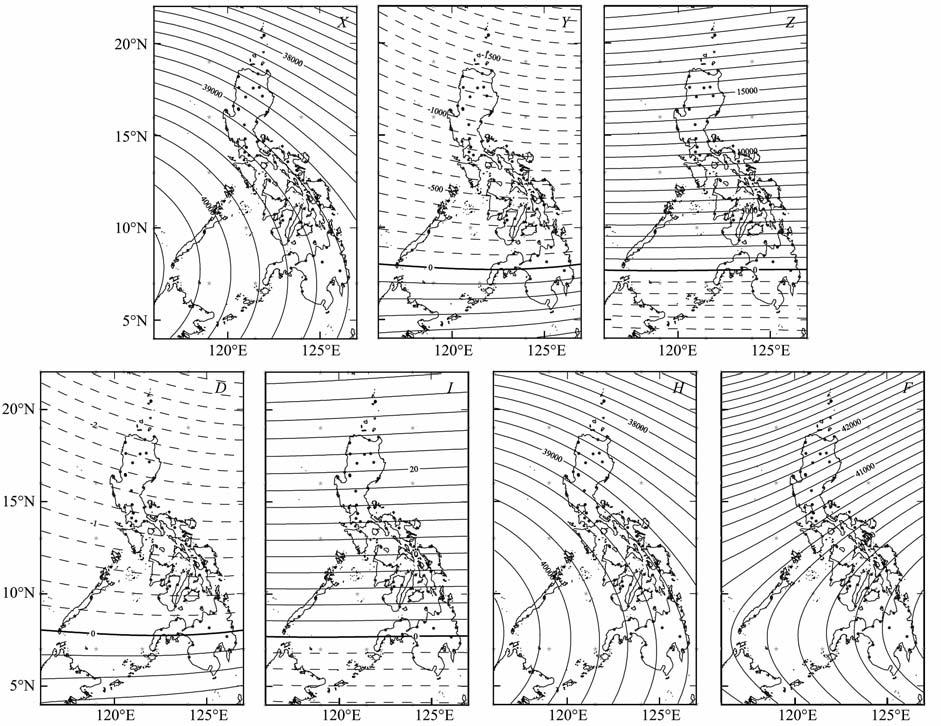
图 4 泰勒多项式模型计算的菲律宾地磁场空间分布(D和I的单位为°,X、Y、Z、H、F单位为nT) Fig. 4 The geomagnetic spatial structure in Philippines by Taylor (D and I,unit:°,X,Y,Z,H and F,unit:nT) |
|
|
表 2 截断阶数为3阶的泰勒系数 Table 2 The coefficients of 3-order Taylor model |
图 4 和图 3 可以看出,泰勒模型计算的X、Y、Z、D、H、I、F七分量的分布与球冠谐模型计算的七分量的分布基本类似.区别在于在泰勒模型中X、H、F出现的拐点要比球冠谐模型表现出的系统拐点舒缓很多.在泰勒模型中D、I、Y、Z四分量的分布走向没有改变,但是等值线的分布要平滑工整许多,以至没有表现出明显的局部特征.
3.3 上述两种模型和IGRF的比较从上面的分析和图知,两种模型X、Y、Z、D、H、I、F七分量的分布形态、数值和零线位置的分布都很相似,这种分布与IGRF 模型的七分量分布也很相似,但是球冠谐模型、泰勒模型和IGRF 模型还是存在差别,下面比较上述两种模型与IGRF的区别.
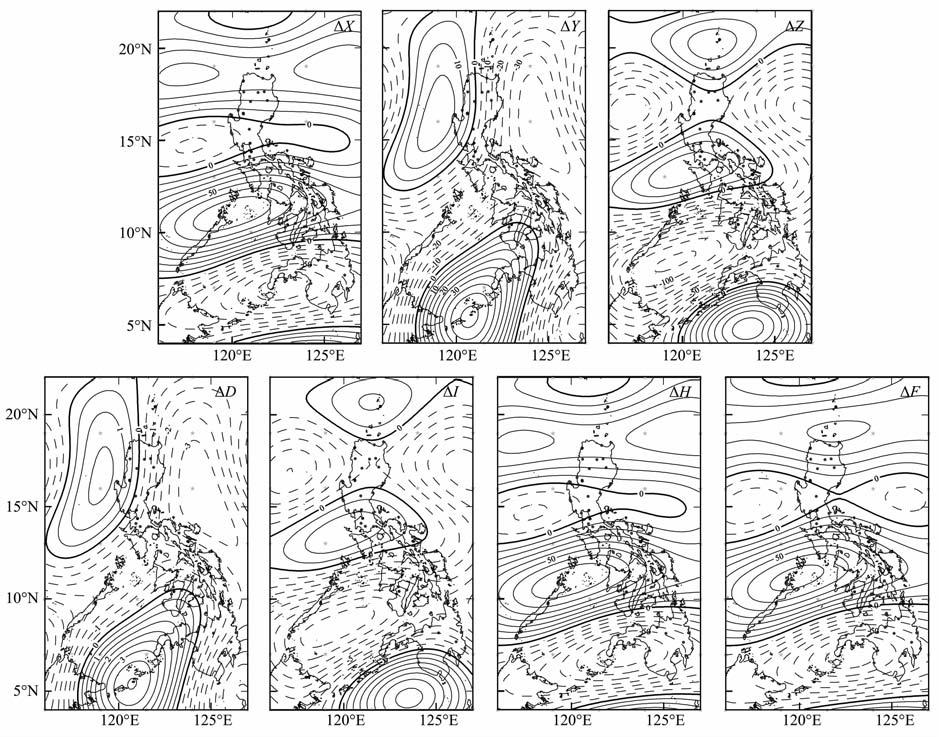
根据球冠谐和与IGRF 差值图(图 5)看出,在球冠谐和IGRF两种模型中,X、Y、Z、D、H、I、F七分量的分布虽然很类似,但却并不完全相同.ΔX、ΔH呈现由高纬到低纬正负异常相间分布的特征,正异常的最大值分布在11°N,120°E,异常中心值都为70nT,最大负异常中心分布于6°N,123°E,异常中心值大于70nT.ΔZ、ΔI出现了东西方向正负相间的不同异常区,在17°N 附近,东西方向出现两个负异常中心,中心最大异常值分别为-20nT、-5′,在13°N出现了正异常中心,最大异常值分别为30nT、3′,在7°N 左右出现另外一个负异常,异常最大值分别在110nT、8′左右,而在5°N,124°E 左右的正异常最大值则分别达到80nT、7′.ΔY、ΔD的分布也几乎一致,在菲律宾的西北和西南分布这两个正异常中心,西北方向的正异常最大值分别为15nT、1.5′,5°N,120°E 处的正异常最大值则高达21nT、4′,ΔY、ΔD在除此之外的区域则分布着负异常,最大异常值分别为-35nT、-3′.ΔF的分布则自北向南依次分布贯穿计算区域的条带状正负异常,20°N左右的正异常中心的最大值大约为40nT,10°N 左右的正异常的最大值为70nT;而与正异常相邻的负异常的异常值分别为30nT(15°N),70nT(5°N).
|
图 5 球冠谐与IGRF差值图(ΔD和ΔI的单位为′,ΔX、ΔY、ΔZ、ΔH、ΔF单位为nT) Fig. 5 The difference between SCH model and IGRF (ΔDandΔI,unit:′,ΔX,ΔY,ΔZ,ΔH and ΔF,unit:nT) |
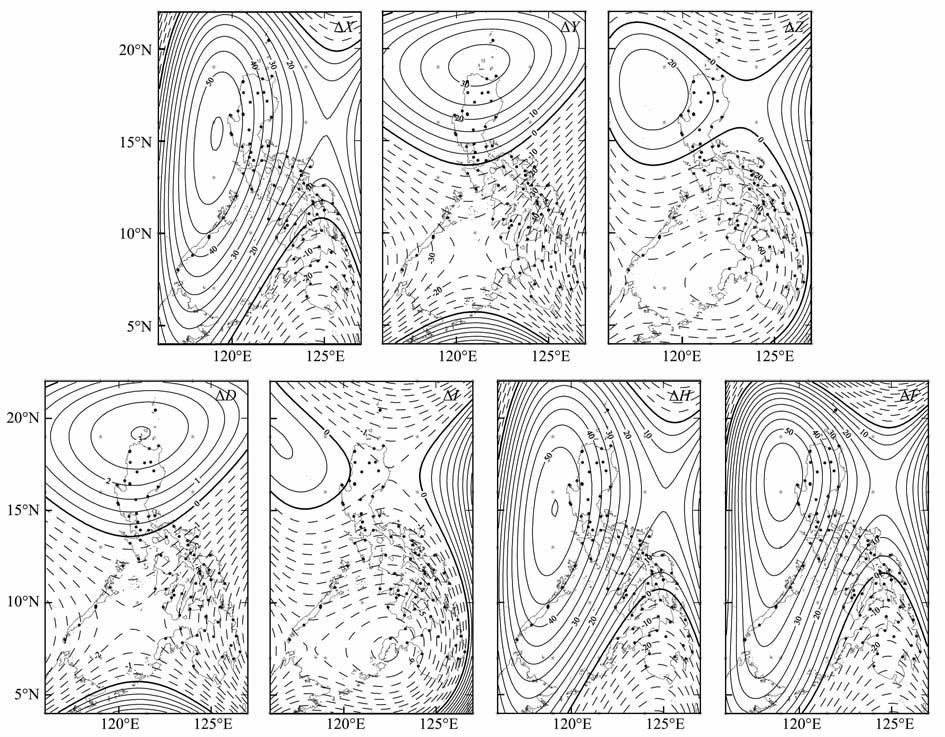
泰勒多项式与IGRF 的差值图(图 6)中各分量的差值分布没有球冠谐与IGRF 的差值图(图 5)零碎,异常的分布要完整.ΔX、ΔH在菲律宾的大部分区域分布着正异常,只有少数区域分布负异常,正异常的最大值为55nT(15°N,119°E),负异常的最大值分布于菲律宾的东南区域,大约为40nT(5°N,126°E).ΔZ,ΔI的分布类似,在所研究区域的大部分地区分布负值,负异常中心值各高达70nT、6.5′(7°N,122°E),正异常只在周边地区很小的范围分布,例如,ΔI在15°N 左右,小于120°E 的范围,分布着小范围的弱正异常,最大异常只在1′左右,对于ΔZ此区域分布的正异常比ΔI范围大些,使得菲律宾此处的陆地分布着20nT 的异常.ΔY、ΔD在5°N~15°N 分布贯穿东西的负异常,其余区域则分布正异常.正负异常最大异常值分别大于50nT、3′(19°N,121°E),-80nT、-7′(9°N,127°E).ΔF只在所研究区域的西北、东南、东北三个角上有负异常分布,负异常的最大值为40nT(17°N,119°E),其余的大部分地区分布着正异常,正异常的最大值高达55nT左右(5°N,125°E).
|
图 6 泰勒多项式与IGRF的差值(ΔD和ΔI的单位为′,ΔX、ΔY、ΔZ、ΔH、ΔF单位为nT) Fig. 6 The difference between Taylor model and IGRF (ΔD and ΔI,unit:′,ΔX,ΔY,ΔZ,ΔH and ΔF,unit:nT) |
(1) 菲律宾地区两种模型的建立都需要精确可靠的测量数据和相关台站的数据资料,不同模型反映的同一地区的地磁场分布形态基本类似,由于建模方法的不同,两种模型在拐点的舒缓度、等值线平滑度等方面存在区别.
(2) 区域地磁场模型截断阶数的选取缺乏统一、有效的标准.综合考虑收敛残差和边界效应,选取5阶球冠谐和模型和3阶泰勒多项式模型描述2005.0年代菲律宾区域地磁场.两者描述的地磁场与 IGRF描述的同期同区域地磁场存在50~100nT左右的差异,这一差异应归结于模型建立过程中采用的大量精确可靠的观测数据.
(3) 球冠谐和模型与IGRF10描述的2005.0年代菲律宾区域地磁场的差异约为80~100nT,泰勒多项式模型与IGRF10 描述的2005.0 年代菲律宾区域地磁场的差异约为40~50nT.球冠谐和与泰勒多项式两种模型的差异应归结于建模方法的不同,且5阶球冠谐和模型描述的地磁场能量较3 阶泰勒多项式模型为多,更能反映区域地磁场的实际分布形态.
| [1] | Ates A, Kearey P, Tufan S. New gravity and magnetic anomaly maps of Turkey. Geophys. J. Int. , 1999, 136(2): 499-502. DOI:10.1046/j.1365-246X.1999.00732.x |
| [2] | Buyuksarac A, Jordanova D, Ates A, et al. Interpretation of the gravity and magnetic anomalies of the Cappadocia region, central Turkey. Pure Appl. Geophys. , 2005, 162(11): 2197-2213. DOI:10.1007/s00024-005-2712-9 |
| [3] | Haines G V, Newitt L R. Canadian geomagnetic reference field 1985. J. Geomag. Geoelectr. , 1986, 38(3): 895-921. |
| [4] | Newitt L R, Haines G V. A Canadian geomagnetic reference field for epoch 1987.5. J. Geomag. Geoelectr. , 1989, 41(2): 249-260. DOI:10.5636/jgg.41.249 |
| [5] | Alldredge L. On regional magnetic charts. J. Geomag. Geoelectr. , 1987, 39: 723-738. DOI:10.5636/jgg.39.723 |
| [6] | Barton C E. Global and regional geomagnetic reference fields. Exploration Geophysics , 1988, 19(3): 401-416. DOI:10.1071/EG988401 |
| [7] | Haines G. Regional magnetic field modeling: a review. J. Geomag. Geoelectr. , 1990, 42: 1001-1018. DOI:10.5636/jgg.42.1001 |
| [8] | Kote M, Haok V. Modelling European magnetic repeat station and survey data by SCHA in search of time-varying anomalies. Phys. Earth Planet. Inter. , 2000, 122(3-4): 205-220. DOI:10.1016/S0031-9201(00)00194-1 |
| [9] | Alldredge L R. Geomagnetic local and regional harmonic analysis. J. Geophys. Res. , 1982, 87(B): 1921-1926. |
| [10] | Chen Z. Review of geomagnetic surveys in China. Science Bulletin , 1944(1): 9-120. |
| [11] | 夏国辉, 郑双良, 吴莉兰, 等. 1980年代中国地磁正常场图及其数学模式. 地球物理学报 , 1988, 31(1): 82–89. Xia G H, Zheng S L, Wu L L, et al. The geomagnetic field chart of China in 1980.0 and the mathematical model. Chinese J. Geophys. (Acta Geophysica Sinica) (in Chinese) , 1988, 31(1): 82-89. |
| [12] | 安振昌. 中国地区地磁场的球冠谐和分析. 地球物理学报 , 1993, 36(6): 753–764. An Z C. Spherical cap harmonic analysis of geomagnetic field for China. Chinese J. Geophys. (Acta Geophysica Sinica) (in Chinese) , 1993, 36(6): 753-764. |
| [13] | Xu W Y, Xia G H, An Z C, et al. Magnetic survey and China GRF2000. Earth, Planets and Space , 2003, 55(4): 215-217. DOI:10.1186/BF03351750 |
| [14] | 徐文耀, 魏志刚, 夏国辉. 2000年中国地区地磁场长期变化的区域特征. 地球物理学报 , 2005, 48(3): 551–560. Xu W Y, Wei Z G, Xia G H. Regional features of the secular variation of the geomagnetic field in China for 2000. Chinese J. Geophys. (in Chinese) , 2005, 48(3): 551-560. |
| [15] | 顾左文, 安振昌, 高金田, 等. 京津冀地区地磁场球冠谐分析. 地球物理学报 , 2004, 47(6): 1003–1008. Gu Z W, An Z C, Gao J T, et al. Spherical cap harmonic analysis on the geomagnetic field in Beijing-Tianjin-Hebei region. Chinese J. Geophys. (in Chinese) , 2004, 47(6): 1003-1008. |
| [16] | 高金田, 安振昌, 顾左文, 等. 地磁正常场的选取与地磁异常场的计算. 地球物理学报 , 2005, 48(1): 56–62. Gao J T, An Z C, Gu Z W, et al. Selection of the geomagnetic normal field and calculations of the geomagnetic anomalous field. Chinese J. Geophys. (in Chinese) , 2005, 48(1): 56-62. |
| [17] | Gu Z W, Zhan Z J, Gao J T, et al. Geomagnetic survey and geomagnetic model research in China. Earth, Planets and Space , 2006, 58(6): 741-750. DOI:10.1186/BF03351977 |
| [18] | Gu Z W, Zhan Z J, Gao J T, et al. Application of GPS in geomagnetic survey. Earth, Planets and Space , 2006, 58(6): 723-729. DOI:10.1186/BF03351974 |
 2011, Vol. 54
2011, Vol. 54