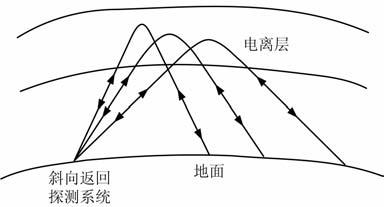
电离层是地球空间环境重要的组成部分,它的变化对人类的生活有着非常重要的影响,并且作为一种天然的电波反射介质而受到人们重视.几十年来,许多学者利用各种观测方式对其进行研究,其中,地面观测方式最为广泛.使用高频无线电波对电离层进行探测,其手段有:垂直探测、斜向探测以及斜向返回探测.垂直探测是垂直向上发射高频无线电脉冲,通过电离层反射,接收在不同频率上由电离层反射的回波,是最古老也是非常重要的电离层地面常规探测方法,能直接获取探测上空的电离层信息,但探测范围小,适用于局部观测.斜向探测则是电波经由发射机斜向发射,经过电离层反射后到达很远的地面,被位于电波覆盖区中某一特定距离上的接收机接收,是一种收发分置的探测方式,通过对斜测结果反演只能获取该距离对应的电离层反射区域信息.斜向返回散射探测则是发射与接收装置位于同一地点,电波在被电离层反射后到达很远的地面,由于地面的不均匀性的散射作用,以致有一小部分能量再经由电离层反射返回到发射点而被接收的过程,如图 1所示.由于斜向返回探测覆盖范围广,能够得到沿探测方向上的大量电离层信息而得到广泛应用.
|
图 1 斜向返回探测原理示意图 Fig. 1 Scheme of backscatter sounding theory |
高频返回散射电离图有两种形式,一种是在固定方位角、探测频率的情况下,进行仰角扫描探测,得到关于返回功率、时延与仰角的三维图形,也称为仰角扫描电离图[1];另一种就是在固定方位角的情况下,进行扫频探测,得到返回功率、时延与频率的三维图形,即扫频电离图[2].对于后者来说,返回散射信号的最重要的特征就是它在时间尺度上的局域分布,即由于跳距聚焦、时间聚焦及电离层球形聚焦等效应,使得电离图一般具有很陡的前沿.高频返回散射电离图包含了探测方向上的电离层的介质和地面(海洋表面)介质的信息,从探测到的电离图反推这些介质的特性就称为电离图反演[3].从原则上来说,扫频探测模式下的返回散射电离图的各部分都含有对电离层结构参数反演的有用信息,然而由于电离层电波传播的复杂性,电离层对电波的吸收及折射、地磁场的影响、电波偏振状态的变化以及地面(海面)散射等诸多因素的共同作用,致使对电离图的利用变得十分困难[2].但是,由于聚焦效应,电离图上有着较清晰的前沿,一般能准确判读,它对电离层电子浓度分布敏感,在信噪比较好的情况下,几乎不受其他条件(如地面特性、天线波束等)的影响.因此最小群时延曲线被广泛利用来进行电离层的反演研究,称之为最小群时延反演问题[4].
目前已有许多关于从电离图推知电离层结构的研究.最开始的以Martyn等效虚高原理为基础,直接把斜测电离图转换为垂测电离图,从而反演出电离层真高剖面[5, 6].稍后则是以曲线拟合为基础的反演方法,随着计算机的发展,该反演方法被广泛采用.一般是假定一个电离层模型,采用矩阵迭代计算来调整其模型参数,使得由该模型产生的最小时延线尽可能逼近电离图前沿,反演用的电离层模型大都采用准抛物(Quasi-Parabolic, QP)电离层模型[7].其中代表性的工作是Rao(1974)[8]用理论合成的电离图前沿以及单层QP模型来反演电离层的三个参数:临界频率、峰高和半厚度.后来许多学者在此基础上做了改进,如Norman[9]将Rao的方法扩展到多层QP 模型.但这些方法均未能对实测电离图前沿进行反演,原因是因为算法对初始模型输入参数要求很严格,且计算过程涉及到大量矩阵方程组运算,导致算法极不稳定,无法应用于实测数据.O.V.Fridman和S.V.Fridman(1994)[10]利用扫频电离图与垂测相结合的方法对仿真电离图进行了反演.随后S.V.Fridman(1998)[11]利用实测数据进行了反演验证并重构了三维电离层结构.Landeau等人[12]使用贝叶斯估计对仰角扫描电离图进行了反演得到临界频率和峰高两个参数,此种方法由于计算时间过长而不适宜用于实测分析.近几年,Norman和Dyson(2006)[13]和Benito等人(2008)[14]成功地对实测的仰角扫描电离图进行了反演,其中 Benito引入了模拟退火方法使得反演过程变得迅速.
本文是在Benito的基础上,对反演方法进行了修改,使得能够成功反演扫频电离图前沿.由于仰角扫描探测设备的研制成本和技术要求太高,很难实现,而扫频电离图的获取则相对容易.基于本文的方法,使得电离层信息的获取具有普适性和工程应用性,且反演算法稳定,计算速度快.本文的第二部分介绍反演算法;第三部分则利用实际探测的高频返回散射电离图对算法进行验证及统计,给出了算法在电离层反演中的具体应用实例及步骤,并重构了沿探测路径方向的二维电子密度剖面;第四部分对实验结果进行分析并给出了结论.
2 反演算法 2.1 电离层模型在任何电离层反演算法开始之前,都必须挑选电离层模型.假设电子密度为准抛物模式[15],表示如下:
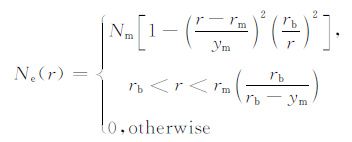
|
(1) |
其中,Ne(r)是距地心r公里处的电子浓度;Nm =fc2/80.6为电子密度最大值;fc 是临界频率;rm 是电子浓度最大值Nm 所处的高度;rb 是电离层底的高度;ym =rm -rb 是电离层半厚度.在单层QP模型下,探测频率为f、发射仰角为β 的信号的群路径P′ 和落点处地面大圆距离D可以精确地计算出来:
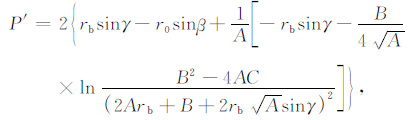
|
(2) |
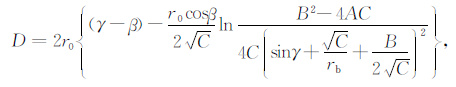
|
(3) |
其中,
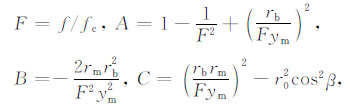
|
γ 为射线在电离层底的入射角,且有rbcosγ =r0cosβ.
从(2)、(3)式中可以看出群路径P′ 和地面大圆距离D的计算中,还涉及到仰角β,因此需要首先对β 进行求解.使群路径P′ 取极小值所对应的仰角,由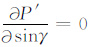

|
(4) |
其中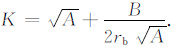
使用黄锡文等[16]对最小群路径射线仰角的求解方法来得到β 的值.方程(4)的近似解为
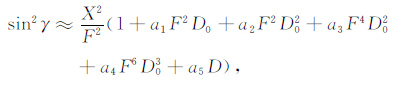
|
(5) |
式中
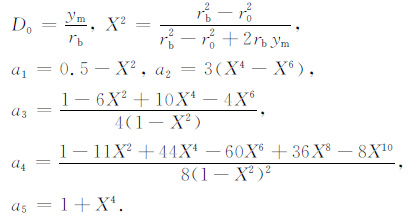
|
由(5)式可得:
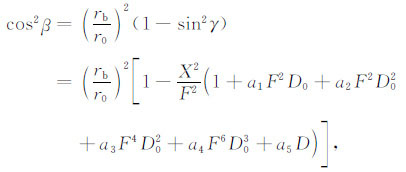
|
(6) |
式中β∈(0°,90°).然后将β 和电离层模型参数代入到(2)和(3)式中便可计算最小群路径P′ 和相应的地面距离D.
2.2 构建反演模型本文中对高频返回散射电离图前沿描迹进行反演以得到电离层的三个参数:临界频率fc、峰高hm(从地面算起)以及半厚度ym.反演需要从原始扫频电离图前沿描迹上选取N(N≥ 3)个点(fi,P′ri)(i=1,2,…,N).然后设定电离层初始模型,设定模型参数搜索空间为(fc, hm, ym),空间参数设定可以参考历史观测数据.在整个模型空间中,计算后验概率密度σp.对文献[14]中的后验概率密度函数进行了改进并且作为反演的目标函数表示如下:
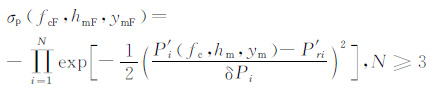
|
(7) |
其中,P′ri是原始电离图前沿描迹上相对应于探测频率fi的实测群路径;P′i(fc, hm, ym)是使用模型参数空间中的参数计算所得的群路径;δPi是P′ri的测量误差,假定为独立高斯分布.在σp 取最小值时所对应的模型参数就是最佳反演结果.
由于要计算出模型空间中所有参数对应的σp并找出其最小值是一个庞大的计算过程,耗时长,不适于实时应用,因此此处采用了模拟退火算法来搜寻最佳结果.模拟退火[17]属于非线性地球物理反演方法的一种,其主要优点是:易于根据具体的物理问题加入约束条件,与其他非线性反演方法相比,模拟退火法不依赖于初始模型的选择,同时在反演过程中不需要计算雅可比矩阵.使用模拟退火对反演过程进行控制后,反演时间大大减少,且反演过程稳定.
3 对实测的高频返回散射电离图的反演 3.1 实验介绍为了验证本文算法的正确性,本文利用武汉大学电离层实验室自主研制的新型武汉电离层斜向返回探测系统(WuhanIonosphericObliqueBackscattering SoundingSystem, WIOBSS)[18, 19]进行斜向返回探测实验,并对实测电离图进行反演.WIOBSS 的技术性能指标如表 1所示.
|
|
表 1 WIOBSS的技术性能指标 Table 1 Specifications of WIOBSS |
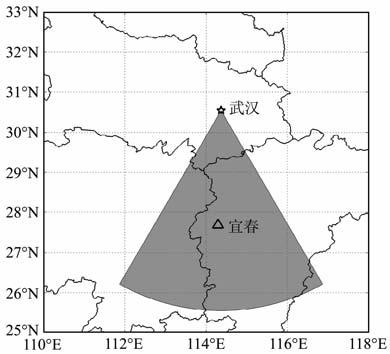
2010年8月26日于武汉大学珞珈山(30.54°N,114.36°E)进行了扫频探测实验,探测方向为正南,探测时间为10∶00~20∶30LT,即全天观测.同时,在宜春(27.69°N,114.29°E)设置了垂测站点进行垂直探测以获得此处上空的电离层临界频率,用于验证斜返探测反演结果.两站相距316.73km.实验示意图如图 2所示.由于斜返电离图的前沿描迹是不同探测频率的跳距聚焦,本文中使用宜春这一单个跳距对实验进行了验证,具有局限性.为了克服该不足之处,采取了多次探测,获取多组实验数据来进行反演对比,并对反演结果进行了统计,以验证本文算法的有效性.
|
图 2 实验站址示意图 Fig. 2 Sketch map of experiment |
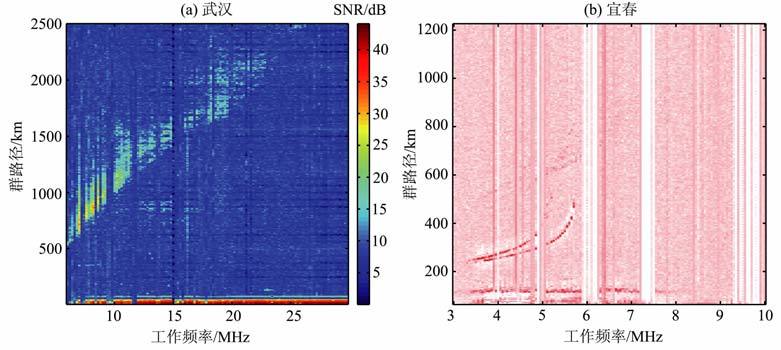
图 3a和图 4a为武汉原始探测扫频电离图,图 3b和图 4b为相应时间的宜春垂测图.由于此次实验探测方向为正南,随着电波传播距离增加,电波在电离层中的反射区的地理纬度降低.而地理纬度对电离层临界频率影响较大,因此,有别于以往反演算法中的只取前沿上的3个点就能得到整个电离层情况,对于跨越纬度的探测结果,前沿的不同部分代表了不同的电离层信息,应该对整个前沿密集采点.为了得到不同地面距离对应的电离层反射区域信息,我们依据探测频率的变化(从小到大)对前沿进行了分段处理,即对所有前沿数据进行了分组处理.一组数据代表了一小段前沿,其反演结果则代表某个区域的电离层信息.当频率间隔取得足够小时,相对于探测范围尺度来说,一组输入数据内对应的反射区域足够小.因此我们假定一组数据对应的反射区域为同一状态,不同分组则为不同状态,这样既符合所选用的电离层模型,不同分组的反演结果也能体现了整个探测方向上电离层的不均匀变化,即局部均匀,整体不均匀.以图 3a为例,通过前沿自动判读处理后,得到的前沿的频率范围是7~22.2 MHz, 以0.1 MHz为间隔,共有153 个数据点,按照探测频率从小到大排列表示为(f1,P′r1),(f2,P′r2),(f3,P′r3),…,(fi,P′ri)(i≤153),其中f1=7 MHz, fi=f1 +0.1(i-1),i≤153.以相邻的每3点为一组且各组数据频率不重叠,则有51 组数据,即前沿被划分为51 段.例如(f1,P′r1),(f2,P′r2),(f3,P′r3)与(f4,P′r4),(f5,P′r5),(f6,P′r6)则是两组数据,需要分别进行反演计算.反演开始前,首先根据历史观测数据,设定合适的电离层参数空间(fc, hm ,ym),然后根据模拟退火方法的原理,设定合适的初始温度T0、终止温度TE 及降温方式,最后输入前沿数据开始反演计算.以一组数据(f1,P′r1),(f2,P′r2),(f3,P′r3)为例,具体反演步骤说明如下:
|
图 3 2010年8月26日20时30分返回散射电离图(a)和垂测图(b) Fig. 3 Ionograms for backscatter (a) and vertical (b) at 20:30LT on 26 August 2010 |
(1) 从电离层参数空间(fc, hm, ym)中随机挑选一组参数(fc0,hm0,ym0)作为电离层初始模型.
(2) 利用表达式(5)和(6)分别计算在探测频率为f1,f2,f3 时最小群路径对应的仰角βmini(i=1,2,3),然后将仰角计算结果代入到表达式(2)中,计算相应的群路径P′i(fc0,hm0,ym0)(i=1,2,3).
(3) 将P′i(fc0,hm0,ym0)、P′ri(i=1,2,3)代入到目标函数表达式(7)中计算σp 的值,记为σp0.
(4) 利用模拟退火方法中依赖于温度的似 Cauchy型概率分布[20],对初始模型进行修改,即在参数空间(fc, hm, ym)内产生一组新电离层模型参数(fc1,hm1,ym1),然后重复步骤(2)和(3),得到新的目标函数值σp1.
(5) 采用Metropo1is准则[17]对σp0和σp1进行判断.令ΔE=σp1 -σp0,如果ΔE≤0,则接受新状态σp1.如果ΔE>0,则计算概率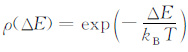
(6) 将步骤(5)中接受的状态及对应的电离层模型作为初始条件,将步骤(4)~(5)重复执行400次(经测试为最佳计算次数),最后保留该温度下得到的最佳目标函数值及电离层参数.
(7) 降温.降温方式采用指数变化的降温模式:T(k)=T0αk,其中k为降温次数,T(k)为第k次降温时的温度,α 为温度衰减因子,α ∈ [0.7,1).
(8) 将降温前的最佳目标函数以及所对应的电离层参数作为降温后的初始模型,并重复步骤(4)~(7).当温度满足T(k)< TE 时,计算中止,保存并输出最终结果.最终所得到的目标函数值即为全局最优值,其所对应的电离层参数则是所需的最佳反演结果.
(9) 将最终反演得到的电离层参数代入表达式(1),得到该组探测数据对应的电波反射区域的电子密度随高度的分布值;使用表达式(3)则可得到反射区域的位置,为地面大圆距离D的1/2,即中点处.
由于图 3a有51 组数据,上述步骤需要重复执行51次,得到51组电离层参数,即整个探测路径上空的电离层参数,累计计算时间163.37s (使用 AMD64X25000+处理器).取出与宜春上空相对应的反演结果,为fc=5.1826 MHz, hm =202.3724km, ym=52.0089km.从图 3b可以得到,宜春上空垂测临频为5.2 MHz, 则临频误差为0.0174 MHz.用同样的处理步骤对图 4a进行计算,得到的反演结果为fc=9.0242MHz, hm=260.3636km, ym=90.2424km, 从图 4b中可得到宜春上空垂测临频为9.1 MHz, 则临频误差为0.0758 MHz.由以上对夜间和日间电离图的反演计算结果可知,反演结果是十分准确的.

|
图 4 2010年8月26日13时30分返回散射电离图(a)和垂测图(b) Fig. 4 Ionograms for backscatter (a) and vertical (b) at 13:30LT on 26 August 2010 |
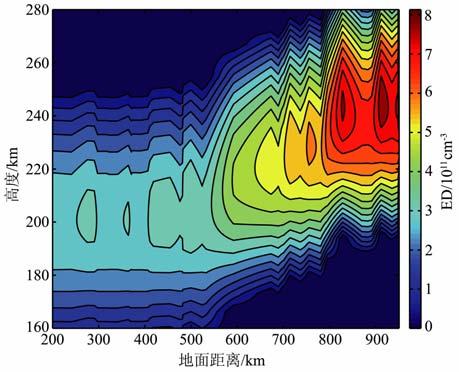
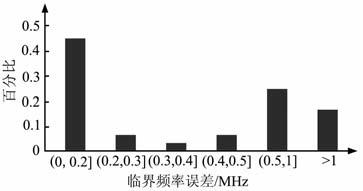
将图 3a中的所有前沿数据反演得到的电离层参数转化为电子密度剖面,即可得到沿探测路径上空的二维电子密度剖面,如图 5所示.此次实验共计获得27组数据,对所有数据进行反演后,统计结果如图 6所示,可以看出62.97% 的反演结果与垂测结果吻合.
|
图 5 二维电子密度剖面横轴是以武汉为起点,正南方向距离探测站的 地面大圆距离;纵轴为距离地面的高度. Fig. 5 Two-dimension electron density protile Wuhan is set as origin, and abscissa is the ground distance southwards to Wuhan; ordinate is the altitude above ground. |
|
图 6 反演结果统计 Fig. 6 Statistics of the inversion results |
从上文中对实测扫频电离图的反演过程可以看出,反演只需要输入扫频图前沿数据即可.通过实验室开发的扫频电离图前沿判读技术,可以迅速直接地将前沿参数载入到反演程序中,避免了以往人工取点造成的延误.然而前沿判读必然会存在一定的误差,即判读结果和实测图上前沿数据的差别,本文算法成功地克服了这一问题,由(7)式中可以看出,在反演过程中已预先加入了判读结果与实测值的误差项,使得反演结果更符合实际情况.对电离图前沿进行分段处理,利用电离层小范围内均匀分布,大范围内非均匀分布的设想,仅用QP 模型就能完整得到整个探测路径上空的电离层信息,避免了以往算法造成的信息残缺和不准确.在对跨纬度探测结果的处理中,能对整个前沿进行反演,计算速度快,几分钟便可得到结果,且程序稳健,能充分满足实时处理要求.若是对东西向的探测图反演,因可以忽略纬度因素造成的影响,则只需前沿的少数几个数据就可得到电离层参数,计算时间则在半分钟之内.
通过与宜春垂测站结果进行对比可知,本文算法对日间和夜间探测均适用,且反演结果十分准确.图 5给出了探测路径上空的二维电子密度剖面,随着地面距离增加(纬度降低),电子密度有着明显的增大趋势(临频增大),符合临频与纬度关系的变化规律,且不依赖于垂测站,仅由斜返探测便可重构电子密度剖面.由图 6可得到,本次实验中62.97%的反演结果与垂测结果吻合情况良好(Δfc≤0.5),85.2%的反演结果与垂测结果的误差没有超过1 MHz.但是,仍有14.8%(Δfc>1)的反演结果误差较大.分析误差较大的这4组数据,可以发现其探测时段在18:00~19:30LT 之间,而此时段恰为日落期间,电离层发生倾斜.电离层倾斜意味着等电子浓度面不再与水平面平行,或者它根本已不再是平面和球面.在日出、日落时间,一般都有明显的东西向倾斜,最显著的表现为日出、日落时电子浓度变化和磁赤道两侧电子浓度随纬度的起伏.一般情况下,若纬度降低,电离层等效薄层高度会增高,且在纬度20°~30°高度达到最大.本次实验垂直探测数据显示,在此期间电离层变化剧烈(一个半小时内临频变化达到2.8 MHz),而本文算法中所采用的电离层模型尚未加入倾斜项,从而不能充分反映此时刻真实电离层结构,因此使得反演结果出现较大误差.实际应用中,可以通过建立先验的模型消除倾斜对电离层反演的影响.这将是我们后续的工作.因此,通过以上分析可以得知,本文反演方法适用于电离层状态变化缓慢,即电离层较平稳时期.
在对斜向返回探测系统的数据处理过程中,电离图反演是一个至关重要的过程.反演得到的电离层参数或者电子密度剖面的正确与否、反演过程是否稳健以及处理时间的长短直接决定了系统的应用前景.本文通过对以往算法进行改进,成功地反演了实测扫频电离图,并画出了二维电子密度剖面.克服了传统算法的耗时、不稳定等特点,展现出该算法在实时处理电离图的优越性---快速、稳健及准确性.在有多层电离层结构时,该算法采用多层QP 模型,探测数据输入方式会改变,这将在另文中作详细阐述.对于电离层变化剧烈的情况,可使用多站联合探测的方式来获取更多的电离层变化信息,对算法进一步改进,加入倾斜及扰动电离层模型,使其适用性更为广泛.
| [1] | Saillant S, Auffray G, Dorey P. Exploitation of elevation angle control for a 2-D HF skywave radar. In: Proceedings of the International Conference on Radar. Australia: IEEE Press, 2003. 662~666 |
| [2] | Coleman C J. On the simulation of backscatter ionograms. Journal of Atmospheric and Solar-Terrestrial Physics , 1997, 59(16): 2089-2099. DOI:10.1016/S1364-6826(97)00038-2 |
| [3] | 熊年禄, 唐存琛, 李行健. 电离层物理概论. 武汉: 武汉大学出版社, 1999 : 386 -399. Xiong N L, Tang C C, Li X J. Outline of Ionosphere Physics (in Chinese). Wuhan: Wuhan University Press, 1999 : 386 -399. |
| [4] | 谢树果. 斜向返回探测电离层参数反演方法研究. 武汉: 武汉大学电子信息学院, 2001 . Xie S G. A study on the ionospheric parameter inversion of backscatter ionograms (in Chinese). Wuhan: School of Electronic Information of Wuhan University, 2001 . |
| [5] | Smith M S. The calculation of ionospheric profiles from data given on oblique incidence ionograms. Journal of Atmospheric and Terrestrial Physics , 1970, 32(6): 1047-1056. DOI:10.1016/0021-9169(70)90116-9 |
| [6] | Rao N N. A note on the analysis of oblique ionograms. Journal of Atmospheric and Terrestrial Physics , 1973, 35(8): 1561-1563. DOI:10.1016/0021-9169(73)90156-6 |
| [7] | Dyson P L, Bennett J A. A model of the vertical distribution of the electron concentration in the ionosphere and its application to oblique propagation studies. Journal of Atmospheric and Terrestrial Physics , 1988, 50(3): 251-262. DOI:10.1016/0021-9169(88)90074-8 |
| [8] | Rao N N. Inversion of sweep-frequency sky-wave backscatter leading edge for quasiparabolic ionospheric layer parameters. Radio Science , 1974, 9(10): 845-847. DOI:10.1029/RS009i010p00845 |
| [9] | Norman R J. Backscatter ionogram inversion. In: Proceedings of the International Conference on Radar. Australia: IEEE Press, 2003. 368~374 |
| [10] | Fridman O V, Fridman S V. A method of determining horizontal structure of the ionosphere from backscatter ionograms. Journal of Atmospheric and Terrestrial Physics , 1994, 56(1): 115-131. DOI:10.1016/0021-9169(94)90181-3 |
| [11] | Fridman S V. Reconstruction of a three-dimensional ionosphere from backscatter and vertical ionograms measured by over-the-horizon radar. Radio Science , 1998, 33(4): 1159-1171. DOI:10.1029/98RS00477 |
| [12] | Landeau T, Gauthier F, Rulle N. Further improvements to the inversion of elevation-scan backscatter sounding data. Journal of Atmospheric and Solar-Terrestrial Physics , 1997, 59(1): 125-138. DOI:10.1016/1364-6826(95)00167-0 |
| [13] | Norman R J, Dyson P L. HF radar backscatter inversion technique. Radio Science , 2006, 41(4): RS4010. |
| [14] | Benito E, Bourdillon A, Saillant S, et al. Inversion of HF backscatter ionograms using elevation scans. Journal of Atmospheric and Solar-Terrestrial Physics , 2008, 70(15): 1935-1948. DOI:10.1016/j.jastp.2008.09.031 |
| [15] | Croft T A, Hoogasian H. Exact ray calculations in a quasi-parabolic ionosphere with no magnetic field. Radio Science , 1968, 3(1): 69-74. DOI:10.1002/rds.1968.3.issue-1 |
| [16] | 黄锡文, 李永俊. 用后向散射电离图前沿确定地物的地面距离. 电波科学学报 , 1986, 1(2): 36–42. Huang X W, Li Y J. Determining the ground range using the HF backscatter ionogram leading edge. Chinese Journal of Radio Science (in Chinese) , 1986, 1(2): 36-42. |
| [17] | Kirkpatrick S, Gelatt C D, Vecchi Jr M P. Optimization by simulated annealing. Science , 1983, 220(4598): 671-680. DOI:10.1126/science.220.4598.671 |
| [18] | Chen G, Zhao Z Y, Zhang Y N. Ionospheric Doppler and echo phase measured by the Wuhan ionospheric oblique backscattering sounding system. Radio Science , 2007, 42(4): RS4007. |
| [19] | Chen G, Zhao Z Y, Yang G B, et al. Enhancement and HF Doppler observations of sporadic-E during the solar eclipse of 22 July 2009. Journal of Geophysical Research , 2010, 115: A09325. DOI:10.1029/2010JA015530 |
| [20] | Ingber L. Very fast simulated re-annealing. Mathematical Computer Modeling , 1989, 12(8): 967-973. DOI:10.1016/0895-7177(89)90202-1 |
 2011, Vol. 54
2011, Vol. 54



