2. 美国阿拉斯加大学费尔班克斯分校地球物理研究所, 阿拉斯加 99701;
3. 中国科学院研究生院,北京 100049;
4. 中国科学院空间天气学国家重点实验室,北京 100190
2. Geophysical Institute, University of Alaska Fairbanks, Fairbanks, Alaska 99701, USA;
3. Graduate University of Chinese Academy of Sciences, Beijing 100049, China;
4. State Key Laboratory of Space Weather, Chinese Academy of Sciences, Beijing 100190, China
太阳瞬时爆发事件驱动的行星际激波到达地球时可压缩磁层,使地球磁层发生扰动.行星际激波在传播过程中还能够使南向磁场增强[1],而较强的南向磁场是造成中等磁暴及大磁暴的主要原因之一[2~5].强烈的地磁扰动往往伴随着行星际激波的到达而产生[6],Echer 和Gonzalez[7]等人通过对1973~2000年间的行星际激波及其对应的地磁效应统计研究发现:激波通过地球后产生弱磁暴(-50nT<Dst<-30nT)、中等磁暴(-100nT<Dst<-50nT)、强磁暴(Dst<-100nT)的几率分别为20.6%,35.1%,22.3%.因此,如何准确地预报行星际激波到达时间对空间天气预报系统的建立具有至关重要的作用[8].同时,行星际激波到达时间还是衡量一个太阳风模式有效性的标准之一[9].
自1997年2月以来,Smith 等人尝试用STOA和ISPM 模型实时预报激波到达时间[10].Fry等人利用HAF 模型模拟了第23 太阳周上升相的173个太阳爆发事件所产生的激波,并把结果和STOA和ISPM 太阳风模型进行了对比[8].McKenna- Lawlor等人利用STOA 和HAF 这两个太阳风模型对23周太阳高年时的166 个太阳爆发事件驱动的激波进行了实时的预报[11].Smith等人对第23太阳周的下降相的行星际激波到达时间做了预报[12].通过太阳周三个相位不同模式对行星际激波到达时间模拟结果的统计表明,这几个太阳风模型在预测激波到达时间的准确程度基本上是相当的.在行星际激波到达时间的预报中,太阳爆发事件的初始激波速度、背景太阳风速度、行星际太阳风的共旋结构以及日地连线和初始激波法向的夹角都是影响激波到达时间预测的因素.同时,动力学理论的研究结果表明,激波不单纯是一个间断,它具有一定的厚度,并且存在许多粒子加速机制(例如,准垂直激波条件下的漂移加速和激波冲浪加速等)[13~15],这些效应会影响激波在行星际空间的传播并且对激波到达时间产生一定的影响.然而在HAF 模型对行星际激波到达时间的预测中,初始激波速度被认为是最重要的[16].因此在本文中主要考虑激波初始速度而忽略其他因素对激波到达时间的影响.在HAF 模型中,初始激波速度可以由米制II型射电爆发的数据计算得到[17].具体的计算方法是Smerd等人首次提出[18]:
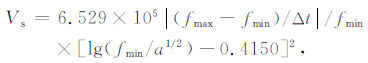
|
(1) |
其中Vs 是初始激波速度(km/s);fmax和fmin分别为此次射电爆发的最大和最小频率;Δt是爆发的持续时间;a是一个常数在计算中取1.上述方法计算得到的激波初始速度为许多太阳风模式提供了输入参数.例如,行星际激波传播模式(ISPM)和激波到时模式(STOA)都利用由上述方法计算得到激波初始速度,并作为模型的输入参数[19~21].然而,Sun等人利用HAF模型模拟了发生在2001年3月28日到4月18日之间的一系列太阳爆发事件[16],通过对模拟的激波到达时间和ACE 卫星的实际观测对比得到计算误差,然后调整激波初始速度使模拟的激波到达时间和观测吻合.结果发现大部分高速激波(Vs>1000km/s)平均需要减小30%才能和观测到的激波到达时间吻合.由于低速的激波到达地球也能引起明显的地磁效应,因此有必要评估相对低速的激波初始速度在激波到达时间预测中的影响.
本文中,我们主要选择具有较低初始激波速度(Vs<1000km/s)的太阳爆发事件.耀斑的参数和激波初始速度由美国阿拉斯加大学费尔班克斯分校的地球物理所提供(http://gse.gi.alaska.edu/recent/archive/).初始的背景太阳风速度由太阳源表面磁场推算得到.模型中,太阳爆发事件的输入参数如下:事件开始时刻、事件持续时间、事件爆发的位置(包括在太阳表面的经度和纬度)、初始激波速度.关于HAF 模型的详细描述可参阅Hakamada, Akasofu[22]和Fry[23]的文章.
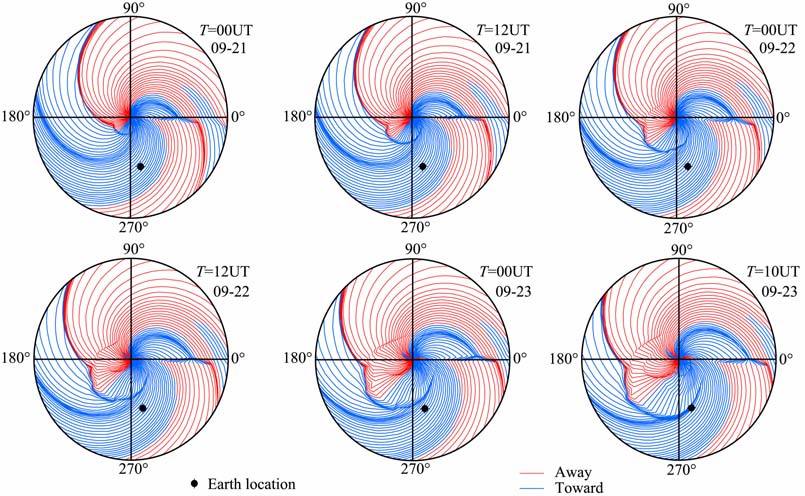
2 模拟以及观测结果图 1展示了2001年9月20日05∶07时刻太阳耀斑爆发时,由这个太阳耀斑驱动的激波在黄道面内传播至2AU 的过程.图的中心表示太阳所在的位置.小黑点代表地球所在位置.图中不同颜色的线代表行星际磁场的极性,红线表示行星际磁场背离太阳,蓝线代表行星际磁场指向太阳.根据公式(1)得到的激波初始速度约为950km/s, 模拟得到激波到达地球的时间为2001年9月23日12∶00左右.根据观测资料,激波到达地球的实际时间是2001年9月23日09∶30左右,模拟的激波到达时间比观测晚了大约2.5h.当激波初始速度(Vs)从950km/s调整到1050km/s后,模拟得到激波到达地球的时间为2001年9月23日09∶00左右,模拟的激波到达时间和观测的基本吻合.此时的1050km/s即为调整后的激波初始速度(Vsi),调整的大小为
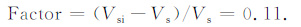
|
|
图 1 2001年9月20日05 :07UT爆发的太阳耀斑驱动的行星际激波在黄道面内传播至2AU的过程 Fig. 1 The propagation in the ecliptic plane to 2 AU of the shock wave generated by the flare occurred at 05 :07UT on September 20th,2001 |
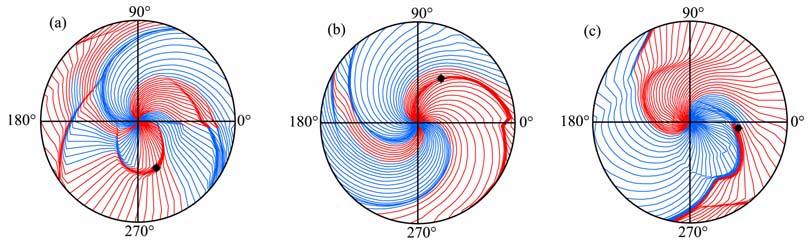
图 2 展示了可能产生激波的三种行星际结构[24].图 2a表示由纯的耀斑或者CME 所产生的激波到达地球;图 2b展示的是由纯粹的共转相互作用区(CIR)产生的激波;图 2c表示由耀斑和CIR 共同作用形成的激波到达地球的情形.起源于太阳冕洞的太阳风高速流传播至行星际空间和背景低速太阳风相互作用,造成接触面内磁场和等离子体的压缩[25],当压缩梯度足够大时,在行星际空间就能形成激波(CIR 驱动的激波).此种情况下,激波并不对应于Type II型射电爆发,因此在我们目前的模拟中无法通过对激波初始速度的调整来改变CIR 产生的激波到达地球的时间.本文仅考虑由耀斑以及耀斑和CIR 相互作用而形成的激波所对应的激波初始速度.
|
图 2 可能产生激波的三种行星际结构[24] (a)纯的耀斑或者CME所形成的激波;(b)共转相互作用区(CIR)形成的激波;(c)耀斑和CIR共同形成的激波. Fig. 2 Three possible interplanetary structures which can generate shock waves[24] (a) Pure flares or CMEs; (b) Pure CIRs; (c) CIR-ICMEs/flares. |
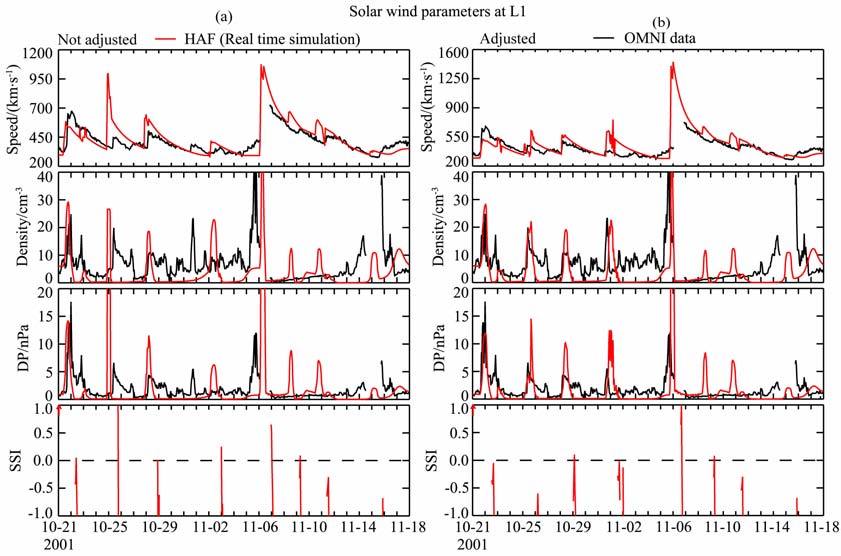
图 3展示了1982卡林顿周的模拟结果和观测结果的对比,其中图 3a的红线表示未调整的激波初始速度的模拟结果,黑线代表卫星的实际观测结果.从上至下依次表示太阳风速度、密度、动压和激波搜索指数.可以看出,大部分的行星际激波到达时间的预报结果和观测结果都有一定的偏差,因此我们根据偏差的大小定量地调整了激波初始速度.图 3b的红线表示激波初始速度调整以后的模拟结果.从图中可以清楚地看出,通过调整激波初始速度可使模拟的结果和观测结果很好地吻合.这也说明了激波初始速度在激波到达时间预报中的重要作用.
|
图 3 1982卡林顿周的模拟结果和观测结果对比 (a)未调整的激波初始速度的模拟和观测结果对比;(b)调整以后的激波初始速度的模拟和观测结果对比. Fig. 3 Comparison between simulated results and observations (a) Simulations before adjustments of the initial shock speed; (b) Simulations after adjustments of the initial sho speed. |
我们对1981至1985卡林顿周期间太阳耀斑爆发所引发的激波初始速度进行上述调整.表 1 列出了能够到达地球的激波事件模拟的结果.第1 列表示耀斑事件的序号;第2 列和第3 列表示耀斑爆发的时间;第4列表示耀斑的爆发位置;第5列表示未调整之前的激波初始速度.第6 列表示利用未调整的激波初始速度模拟得到的激波到达时间.在这列中,“InteractingEvent"表示对应的太阳耀斑事件所产生的激波被后面爆发的耀斑所产生的激波赶超并相互作用形成一个新的激波.这种类型的激波事件已由McKenna-Lawlor等人进行了详细的描述[11].第7列表示使模型预测得到的激波到达时间和观测结果相吻合所调整的初始激波速度.第8 列表示观测结果得到的激波到达时间.第9 列是激波初始速度的调整因子Factor= (Vsi-Vs)/Vs, 它代表激波初始速度调整的百分比.在模拟中通过设定激波搜索指数SSI=log(ΔDP/DP)来确定激波是否到达地球.其中DP是地球附近太阳风动压;ΔDP=DP(t+1)-DP(t)是两个连续时刻的太阳风动压变化值.当这个指数值超过-0.5 时,就认为激波到达地球[16].
|
|
表 1 模拟激波到达时间和观测对比 Table 1 Comparisons of the shock arrival time between simulated and observed results |
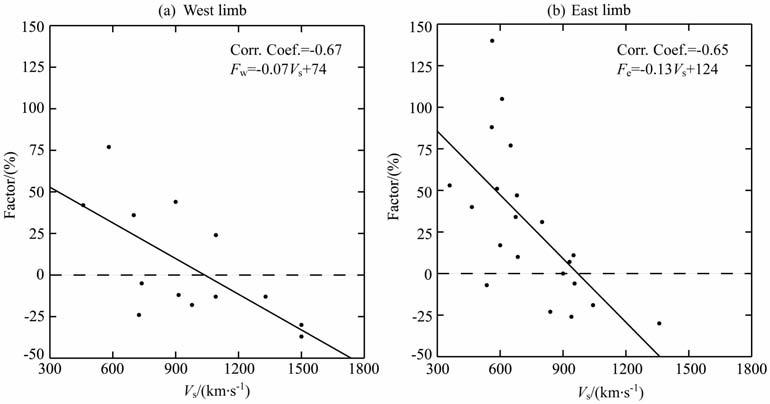
图 4展示了经过调整激波初始速度后1981 至1985卡林顿周的22 个激波到达地球的黄道面投影.根据卫星观测结果,在1981到1985卡林顿周中有22个激波到达地球,而HAF 模型的模拟结果有27个激波能够到达地球.其中对第5,7,22,25,46个耀斑事件进行模拟(未在表格中列出),预测将有激波到达地球,但是实际上却没有被观测到.从图中可以看出第1,10,21,32,34,38和44个耀斑事件对应的激波是由CIR 和耀斑相互作用产生的;而最后一个激波事件是由纯粹的CIR 产生的;其余的则是由纯粹的耀斑事件产生的.一般来说,由耀斑引发的激波由于其在太阳上出现位置的不同,即使初始激波速度完全相同,激波到达地球所需的时间也不尽相同,特别是对于那些分别发生在太阳东西两个半球的耀斑其影响可能更明显.Fry 等人通过68个激波事件的激波平均传播速度(日地距离除以传播时间)和激波初始速度的比值(Vave/Vs)和耀斑在日面上的经度的对比发现,在大部分的经度初始激波速度都有被高估的趋势,这种趋势在西半球尤为明显[8].因此为了考虑耀斑位置的影响,我们把耀斑分为发生在太阳东半球和西半球两类来进行分析.图 5a展示的是在西半球爆发的太阳耀斑事件经过上述方法调整激波初始速度后得到的分布图,其中纵坐标表示调整因子(Fw),横坐标表示未调整前的激波初始速度(Vs).利用线性回归方法得到回归方程为:Fw = -0.07Vs+74,相关系数为-0.67.当Vs=1057km/s时,Fw=0.这意味着对于未调整前的激波初始速度低于1057km/s的事件,激波初始速度整体趋势被低估,而高于1057km/s的事件整体趋势被高估.图 5b展示的是在东半球爆发太阳耀斑事件对应的调整因子(Fe)和激波初始速度的相互关系.此时的回归方程为:Fe= -0.13Vs+124,相关系数为-0.65.Fe=0时,给出Vs=954km/s.因此对于东半球爆发的太阳耀斑事件,未调整前的激波初始速度在低于954km/s时整体趋势被低估,而高于954km/s时整体趋势被高估.对于东西半球高速激波事件(Vs>1000km/s)和Sun等人[16]的结论是基本一致的.

|
图 4 调整激波初始速度以后1981至1985卡林顿周的22个激波到达地球的黄道面投影图 Fig. 4 Shock arrivals at Earth of the 22 shock waves after adjusting the initial shock speed |
|
图 5 调整因子Factor关于初始激波速度的分布图 (a)西半球爆发的耀斑事件;(b)东半球爆发的耀斑事件. Fig. 5 The distribution of the corrective factors in terms of Vs (a) Solar flares occurred on the western hemisphere; (b) Solar flares occurred on the eastern hemisphere. |
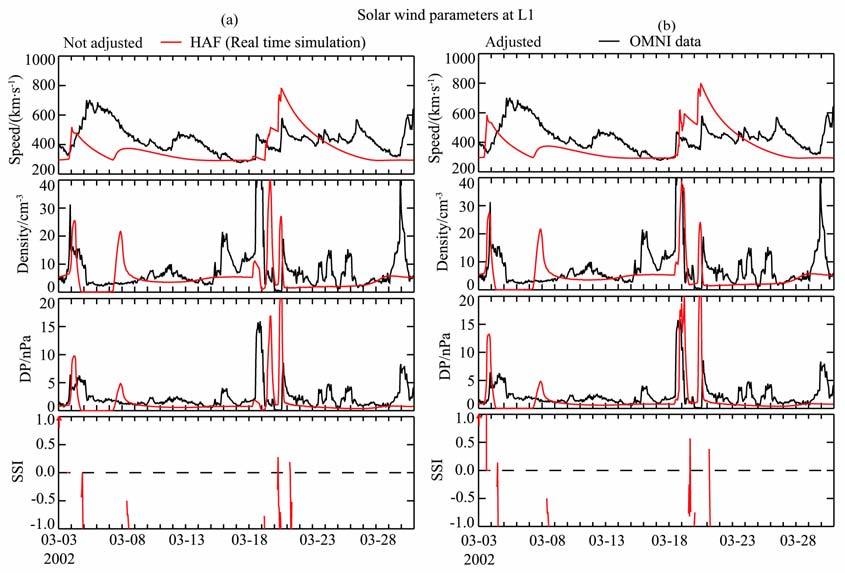
为了验证以上得到回归方程在改善激波到达时间预测的有效性,我们利用这两个方程对随后5 个(1986~1990)卡林顿周期间的太阳耀斑事件所对应的激波初始速度进行修正,并利用修正前和修正后的激波初始速度分别进行模拟对比.图 6 给出了相应于1987卡林顿的结果.图中的参数和图 3一致.其中图 6a是利用未调整的激波初始速度的模拟和观测结果的对比,而图 6b是激波初始速度经以上回归方程修正后的对比.可以清楚地看出,经过对激波初始速度进行修正后,激波到达时间有较明显的改善.特别是对于3月18 日激波事件,平均绝对误差由原来的18h降低为6h左右.对这5个卡林顿周所有事件模拟结果的误差统计分析表明,对于西半球的耀斑事件平均绝对误差由未经调整的16h 降低到了12h左右,而对于东半球的耀斑事件则由未经调整的15h 降低到了11h 左右.这说明我们以上所得到的结果对于提高HAF 模型激波到达时间的预报水平方面是比较有效的.
|
图 6 1987卡林顿周的模拟结果和观测结果对比 (a)未调整的激波初始速度的模拟和观测结果对比;(b)利用统计关系修正后的激波初始速度的模拟和观测结果对比. Fig. 6 Comparison between simulated results and observations (a) Simulations before adjustments of the initial shock speed; (b) Simulations after adjustments of the rnitial shock speed by using the statistical functions. |
本文利用HAF太阳风模型,对1981到1985卡林顿周的太阳耀斑事件进行模拟,在和卫星实际观测对比的基础上,对激波初始速度调整可使预测得到的激波到达时间和观测结果很好地吻合.通过对发生在太阳上东西两个半球耀斑爆发引发激波事件到达地球时间模拟结果的统计分析,得到调整因子和激波初始速度的统计关系分别为Fw = -0.07Vs+74 和Fe=-0.13Vs+124.利用这两个关系对1986 到1990卡林顿周的太阳耀斑对应的激波初始速度进行修正,并用修正前后的激波初始速度分别进行模拟检验.所得到的结果和卫星实际观测对比表明,对于位于西半球的耀斑,行星际激波到达地球所需时间的平均误差从16h 降低到12h, 而对于位于东半球的耀斑,行星际激波到达地球所需时间的平均误差从15h降低到11h.因此对激波初始速度采用以上的修正可以提高HAF 对激波到达时间的预报水平.
致谢感谢美国阿拉斯加大学费尔班克斯分校地球物理研究所提供耀斑数据和激波初始速度.感谢 WSO 提供太阳源表面磁场数据.感谢NASA 戈达德空间飞行中心提供OMNI数据.
| [1] | Gosling J T, McComas D J, Phillips J L, et al. Geomagnetic activity associated with Earth passage of interplanetary shock disturbances and coronal mass ejections. J. Geophys. Res. , 1991, 96(A5): 7831-7839. DOI:10.1029/91JA00316 |
| [2] | Russell C T, McPherron R L, Burton R K. On the cause of geomagnetic storms. J. Geophys. Res. , 1974, 79(7): 1105-1109. DOI:10.1029/JA079i007p01105 |
| [3] | Gonzalez W D, Tsurutani B T. Criteria of interplanetary parameters causing intense magnetic storms (Dst<-100 nT). Planetary and Space Science , 1987, 35(9): 1101-1109. DOI:10.1016/0032-0633(87)90015-8 |
| [4] | Gonzalez W D, Tsurutani B T, Gonzalez A L C, et al. Solar wind-magnetosphere coupling during intense magnetic storms (1978-1979). J. Geophys. Res. , 1989, 94(A7): 8835-8851. DOI:10.1029/JA094iA07p08835 |
| [5] | 刘绍亮, 李立文. 南向行星际磁场事件与磁暴关系的研究. 地球物理学报 , 2002, 45(3): 297–305. Liu S L, Li L W. Study on relationship between southward IMF events and geomagnetic storms. Chinese J. Geophys. (in Chinese) , 2002, 45(3): 297-305. |
| [6] | 刘四清, 魏奉思. 耀斑-行星际激波结构与相应地磁扰动结构间关系的分析(Ⅰ). 地球物理学报 , 1993, 36(6): 691–698. Liu S Q, Wei F S. Structures of flare-interplanetary shock waves and geomagnetic disturbance. Chinese J. Geophys. (Acta Geophysica Sinica) (in Chinese) , 1993, 36(6): 691-698. |
| [7] | Echer E, Gonzalez W D. Geoeffectiveness of interplanetary shocks, magnetic clouds, sector boundary crossings and their combined occurrence. Geophys. Res. Lett. , 2004, 31: L09808. DOI:10.1029/2003GL019199 |
| [8] | Fry C D, Dry M, Smith Z, et al. Forecasting solar wind structures and shock arrival times using an ensemble of models. J. Geophys. Res. , 2003, 108(A2): 1070. DOI:10.1029/2002JA009474 |
| [9] | Sun W, Dryer M, Fry C D, et al. Real-time forecasting of ICME shock arrivals at L1 during the "April Fool's Day" epoch: 28 March-21 April 2001. Ann. Geophys. , 2002b, 20(7): 937-945. DOI:10.5194/angeo-20-937-2002 |
| [10] | Smith Z, Dryer M, Ort E, et al. Performance of interplanetary shock prediction models: STOA and ISPM. J. Atmos. Solar-Terr. Phys. , 2000, 62(14): 1265-1274. DOI:10.1016/S1364-6826(00)00082-1 |
| [11] | McKenna-Lawlor S M P, Dryer M, Kartalev M D, et al. Near real-time predictions of the arrival at Earth of flare-related shocks during Solar Cycle 23. J. Geophys. Res. , 2006, 111: A11103. DOI:10.1029/2005JA011162 |
| [12] | Smith Z K, Dryer M, McKenna-Lawlor S M P, et al. Operational validation of HAFv2's predictions of interplanetary shock arrivals at Earth: Declining phase of Solar Cycle 23. J. Geophys. Res. , 2009, 114: A05106. DOI:10.1029/2008JA013836 |
| [13] | Yang Z W, Lu Q M, Wang S. The evolution of the electric field at a nonstationary perpendicular shock. Phys. Plasmas , 2009, 16(12): 124502. DOI:10.1063/1.3275788 |
| [14] | Lu Q M, Hu Q, Zank G P. The interaction of Alfvén waves with perpendicular shocks. Astrophys. J. , 2009, 706(1): 687-692. DOI:10.1088/0004-637X/706/1/687 |
| [15] | Yang Z W, Lu Q M, Lembège M B, et al. Shock front nonstationarity and ion acceleration in supercritical perpendicular shocks. J. Geophys. Res. , 2009, 114: A03111. DOI:10.1029/2008JA013785 |
| [16] | Sun W, Dryer M, Fry C D, et al. Evaluation of solar Type II radio burst estimates of initial solar wind shock speed using a kinematic model of the solar wind on the April 2001 solar event swarm. Geophys. Res. Lett. , 2002a, 29(8): 1171. DOI:10.1029/2001GL013659 |
| [17] | Maxwell A, Dryer M. A piston-driven shock in the solar corona. Space Sci. Rev. , 1982, 32: 11. |
| [18] | Smerd S F, Sheridan K V, Stewart R T. Split-band structure in Type II radio bursts from the Sun. Astrophys. Lett. , 1975, 16(1): 23-28. |
| [19] | Smith Z, Dryer M. MHD study of temporal and spatial evolution of simulated interplanetary shocks in the ecliptic plane within 1 AU. Solar Phys. , 1990, 129(2): 387-405. DOI:10.1007/BF00159049 |
| [20] | Dryer M, Smart D F. Dynamical models of coronal transients and interplanetary disturbances. Adv. Space Res. , 1984, 4(7): 291-301. DOI:10.1016/0273-1177(84)90200-X |
| [21] | Smart D F, Shea M A. A simplified model for timing the arrival of solar flare-initiated shocks. J. Geophys. Res. , 1985, 90(A1): 183-190. DOI:10.1029/JA090iA01p00183 |
| [22] | Hakamada K, Akasofu S I. Simulation of three-dimensional solar wind disturbances and resulting geomagnetic storms. Space Sci. Rev. , 1982, 31(1): 3-70. DOI:10.1007/BF00349000 |
| [23] | Fry C D. Three-dimensional structure of the heliosphere: Quiet-time and disturbed periods. Univ. of Alaska Faribanks , 1985. |
| [24] | Zhang Y, Sun W, Feng X S, et al. Statistical analysis of corotating interaction regions and their geoeffectiveness during solar cycle 23. J. Geophys. Res. , 2008, 113: A08106. DOI:10.1029/2008JA013095 |
| [25] | Hundhausen A J. Coronal Expansion and Solar Wind. Berlin, New York: Springer-Verlag, 1972 . |
 2011, Vol. 54
2011, Vol. 54



