瞬变电磁法具有快速探测能力、较好的空间分辨率等优点,近年来被广泛用于矿产勘查和水文环境探测等领域[1~10].该探测方法的原理是:瞬变电磁波在向地下传播的过程中,受到各个地层中不同介质的衰减,不同介质对不同频率的瞬变电磁波衰减值是不同的.因此,只要提取出回波信号中对应于不同物质的晚期瞬变电磁信号的特征频谱,就可反演出地层中不同物质.但是瞬变电磁检测接收机采集到的晚期信号是相当微弱的,目前的晚期瞬变电磁信号检测大多采用波形叠加的方法.这种方法对晚期瞬变电磁信号的频率有较多限制,在信噪比较高的强噪声背景下,难以提取出目标信号,这就降低了瞬变电磁设备的探测深度和准确率.传统的瞬变电磁检测方法需要接收几十个甚至更多周期的原始信号进行多点平均和信号叠加[4],才能得到目标信号,因此信号采集时间比较长,数据采集量比较大,这也加大了仪器设计的难度.
随机共振系统是用于弱信号检测的方法之一[11~16],当信号和噪声之间存在某种匹配时,噪声能量就会向信号能量转移,输入信号的信噪比不仅不会降低,反而会大幅度地增加,这为研究在强噪声背景下提取匹配的弱周期信号提供了新的思路.自1981年Benzi等提出随机共振[13]以来,人们对随机共振相关理论及其在各个工程领域的应用已经做了大量的研究[10, 12],并认识到随机共振现象在自然界广泛存在.虽然已有的绝热近似和线性响应理论,使得随机共振在一定程度上得到了应用,然而这些理论仅适用于小参数信号(小幅度、小频率、小噪声).为了扩展随机共振在信号检测领域的应用范围,人们分别提出了调制信号的随机共振[12]和二次采样随机共振[14, 15]用于高频信号检测,但这些方法都是针对待测信号频率已知的单一频率的高频信号检测.此外,还有人提出了多信号叠加在随机共振系统中的检测方法[17, 18],但研究的只是多个小频率信号叠加的检测方法.接收到的晚期瞬变电磁信号是大参数、多频率且各频率分量未知的强噪声背景下的弱信号[4],因此,传统的随机共振方法并不适用.因此,本文提出一种尺度变换随机共振瞬变电磁弱信号检测方法,通过引入尺度变换,消除了随机共振系统对待测目标信号的频率限制,并以共振频率的形式自适应地测出原始含噪晚期瞬变电磁信号中的目标频率,该系统能自适应地检测出全频段的周期弱信号.
2 尺度变换随机共振的晚期瞬变电磁弱信号检测方法 2.1 随机共振原理随机共振系统一般以非线性朗之万方程作为研究的理论模型,在含有噪声和周期激励情况下,考虑双稳势中Brownian质点的过阻尼运动[9]:
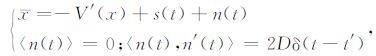
|
(1) |
式中V(x)表示映像对称平方势.
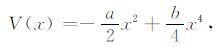
|
(2) |
式(1)可写为
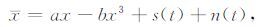
|
(3) |
其中,s(t)为目标信号,n(t)是均值为0、强度为D的高斯白噪声,x为系统输出,a和b为非线性系统结构参数,当s(t)=Acos(wt+Φ)时,输入外力为高斯噪声驱动的余弦信号,调整参数a和b,该余弦信号可在双阱之间跃迁,实现共振. 为信号频率,Φ 为信号相位角,A为信号幅度,A和D的单位均为任意单位.在没有信号和噪声输入时,方程(3)描述了一个有两个对称势阱的非线性系统,其底部位于x1,2=±$\sqrt{a/b}$位置,而中央势垒高度为ΔV =0.25a2/b.
2.2 尺度变换原理
对信号进行尺度变换,即令时域信号ns(t)的频域为NS(jw),则ns(mt)的频域为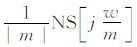
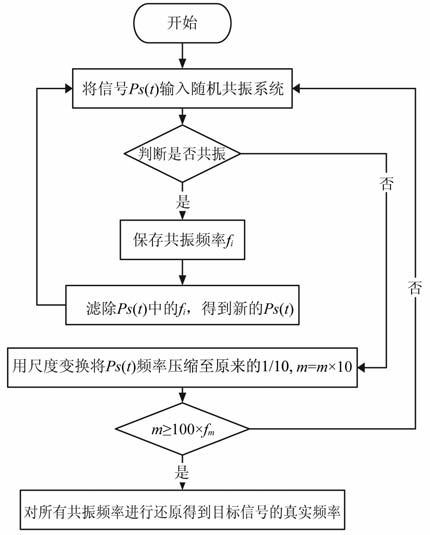
尺度变换随机共振瞬变电磁弱信号检测算法的流程图如图 1所示,具体步骤如下:
|
图 1 算法流程图 Fig. 1 The flow chart |
步骤1:将含噪晚期瞬变电磁信号Ps(t)输入随机共振系统;
步骤2:调整参数a和b[19],判断系统是否共振,若发生共振,则保存引起共振的频率fi;否则,跳转到步骤4;
判断系统是否共振的方法:首先,将噪声n(t)输入随机共振系统,对输出信号进行功率谱估计,得到噪声平均功率谱强度Pn;然后,将信号Ps(t)输入共振系统,对输出信号进行功率谱估计,当输出信号的功率谱中检测到有满足功率谱强度Pfi>300×Pn的频率fi,即发生了共振,共振频率为fi.
步骤3:在Ps(t)中,滤除步骤2中检测到的所有共振频率fi,得到新的Ps(t),跳转到步骤1;
步骤4:令m为记录压缩倍数的标记,初值为1,m=m×N,N为正整数,一般选择N=10.如果m小于目标信号最高频率的10~100 倍,用尺度变换将信号Ps(t)频域压缩至原来的$\frac{1}{m}$,得到新的Ps(t),之后跳转到步骤1;如果m大于或等于目标信号最高频率的10~100倍,跳转到步骤5;
针对具体的应用领域,可以估计待测的目标信号的频率范围,为了保证全部提取出目标信号,将估计的待测目标信号的最高频率扩大10~100 倍,作为m的上限值.
步骤5:对各共振频率fi进行还原,即各共振频率fi分别乘以获得该共振频率时的m值,得到目标信号的真实频率.
3 尺度变换随机共振的瞬变电磁弱信号检测应用实例尺度变换的随机共振瞬变电磁弱信号检测方法在某地质实地勘测中使用情况:瞬变电磁探测接收信号为Ps(t),Ps(t)= P(t)+n(t),s(t)为目标信号,P(t)= ΣAicos(wit)为多个不同频率信号的叠加,其中:Ai为目标信号幅度,其大小对系统影响很小,不作考虑,wi为目标信号频率,其范围是1~100000Hz.n(t)是强度D≈48.5 的高斯白噪声,由于用瞬变电磁法探测接收的晚期信号是强噪声背景下的弱信号,相对噪声来说目标信号能量很小,所以噪声强度用接收的含噪信号的平均强度近似,本例含噪信号平均强度为48.5.所用随机共振系统参数为a=0.1,b=1.
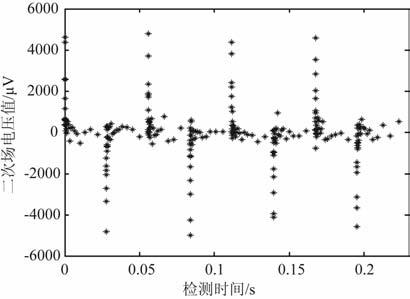
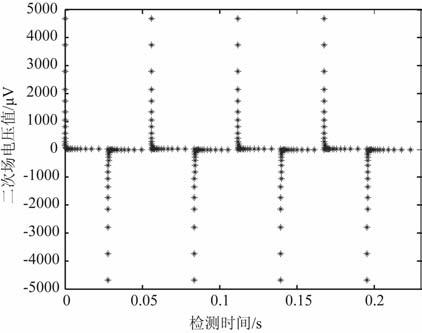
图 2为接收机在测点号为100处采集到的原始含噪瞬变电磁信号图(为了便于观察,图中仅显示4个周期的采集信号);
|
图 2 接收机采集到的原始含噪瞬变电磁信号 Fig. 2 The original signal mixed noise collected by TEM receiver |
按照尺度变换算法,m从1递增到100时,依次输入随机共振系统如图 3所示.

|
图 3 无频率分量共振(a)m=1;(b)m=10(c);m=100. Fig. 3 No frequency resonance |
当m=1,10,100,由于此时晚期瞬变电磁信号含的频率不符合随机共振系统绝热条件,故均未发生共振,亦即原始信号没有含小频率分量.
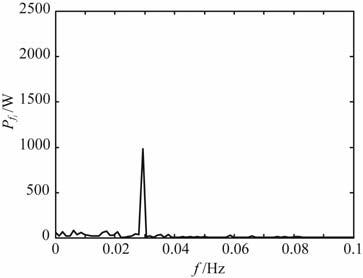
当m=1000时,信号输入随机共振系统,如图 4所示,0.03275Hz频率发生共振.
|
图 4 0.03275 Hz频率分量共振 Fig. 4 0.03275 Hz resonance |
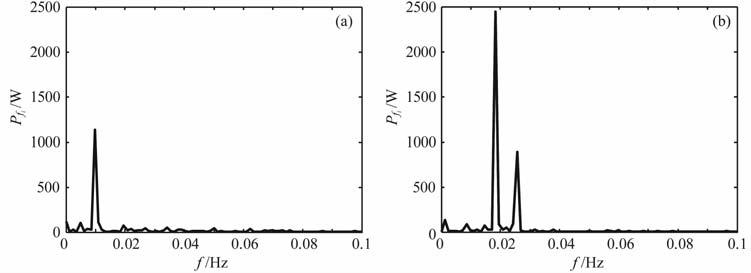
滤除32.72Hz频率成分其余信号再压缩至原来的1/10(即:m=10000)时,剩余信号输入随机共振系统,如图 5所示,3个频率分量发生共振.
|
图 5 m=10000时,三个频率分量发生共振(a)0.00999Hz频率分量共振;(b)0.0166Hz、0.0233Hz频率分量共振. Fig. 5 m=10000,3 frequnceies resonance |
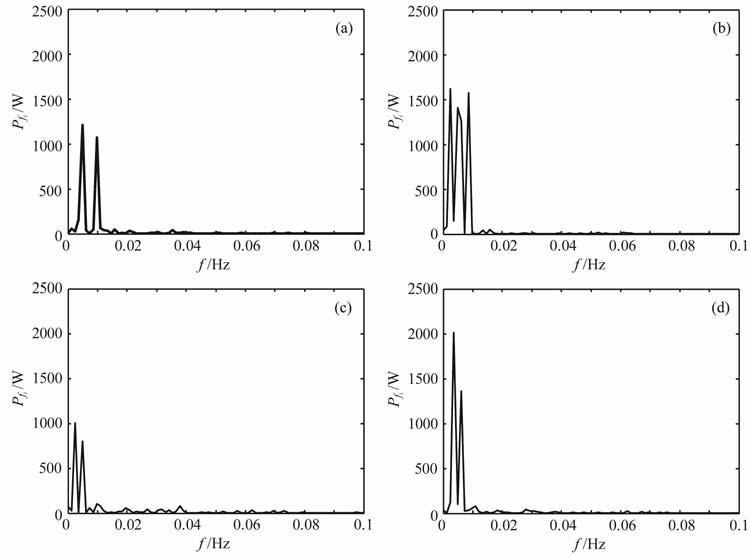
再滤去99.9,166,233 Hz的频率成分,继续压缩至原来的1/10(即:m=100000),剩余信号输入随机共振系统,如图 6所示,9个频率分量发生共振.
|
图 6 m=100000时,9个频率分量发生共振(a)0.00767Hz、0.00967Hz频率分量共振;(b)0.00300Hz、0.00500Hz、0.00833Hz频率分量共振;(c)0.00366Hz、0.00699Hz频率分量共振;(d)0.00434Hz、0.00567Hz频率分量共振. Fig. 6 m=100000,9 frequnceies resonance |
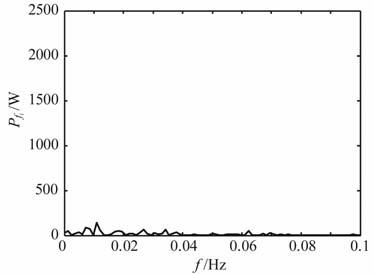
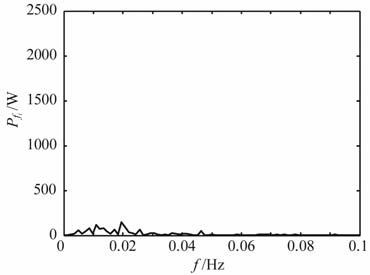
滤去300,366,434,500,567,632,699,767,833,901,967Hz频率,继续压缩至原来的1/10(即:m=1000000),如图 7 所示,无共振频率发生;继续压缩1/10(即:m=10000000)如图 8所示,仍旧没有共振频率发生.
|
图 7 无频率分量发生共振 Fig. 7 No frequency resonance |
|
图 8 无频率分量发生共振 Fig. 8 No frequency resonance |
|
|
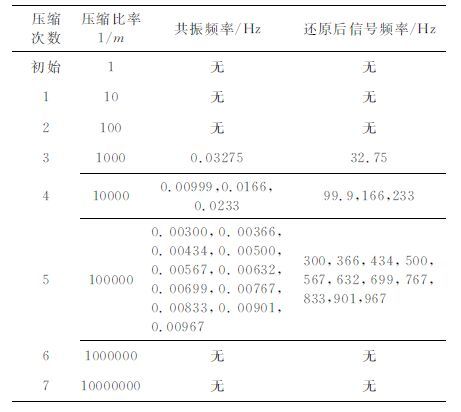
表 1 尺度变换随机共振的瞬变电磁弱信号检测过程 Table 1 The process of scale trans for mationfor detecting TEM weak signal of SR |
表中列出了已提取到的全部目标信号频率,所有频率的叠加即得到原始信号.各个频率分量叠加再变换到时域可得图 9所示信号.
|
图 9 尺度变换随机共振提取目标信号 Fig. 9 Scale transformation for detecting TEM signal of SR |
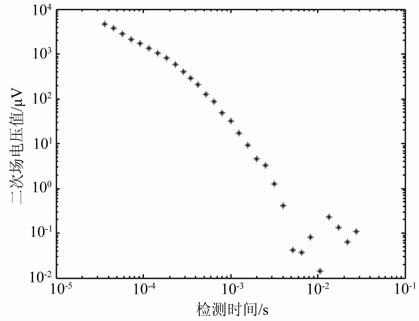
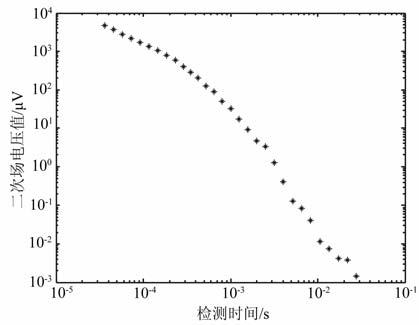
图 10为对接收机在测点100处采集到的50个周期原始含噪瞬变电磁信号,采用三点平均法进行叠加得到的效果图(为了便于观察,图中以双对数坐标进行显示);图 11为采样本文方法提取目标信号,取前14个周期的信号进行叠加绘制的双对数坐标图.
|
图 10 三点平均法在50个周期的信号叠加得到的双对数坐标图 Fig. 10 The double logarithmic plot of three-point averagein 50 cycles of signal superposition |
|
图 11 取14半个周期的信号绘制的双对数坐标图 Fig. 11 The double logarithmic plot of 14 hal--cycle signal |
从图 10可以看出,采用传统方法提取目标信号时,晚期信号已经不是平滑衰减,信号杂乱,无法提取出深层末端晚期微弱信号;从图 11 可以看出,尺度变换的随机共振方法在提取深层目标信号时,弱晚期信号仍满足平滑衰减,波形信号为有用信号,因此有更好的探测深度.
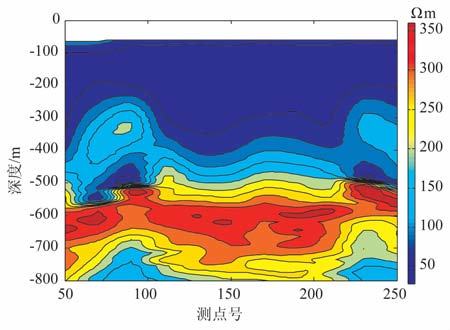
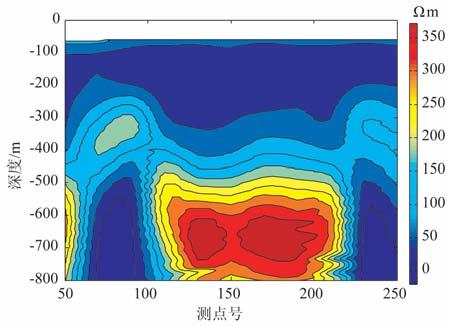
图 12 和图 13 为应用美联公司生产的TVLF-1000瞬变电磁仪在广西某煤矿用大定源方式进行的实地测量,1000m×1000m 矩形发射框,双极性梯形脉冲供电,脉宽27.9 ms, 关断时间为731μs, 供电电流为28A.工区靠近城市,电磁干扰较大,在整个工区布置了10条测线,这里是其中一条测线的处理结果(L3线),测线上12 个测点分别用原始方法和尺度变换随机共振方法提取的目标信号进行反演后绘制剖面对比,其中,图 12 为采用三点平均和50个周期的信号叠加提取目标信号的方法得到的剖面图,图 13为采用尺度变换随机共振方法提取目标信号的方法得到的剖面图.所测地质实际地质形貌为,测点80~240所在位置地下100~200m之间有水仓,测点50~100和230~250所在位置地下500~800m 之间为含水砾岩层.
|
图 12 三点平均法提取目标信号绘制的剖面图 Fig. 12 The protile was made by target signal extractedby three-point average method |
|
图 13 尺度变换随机共振取目标信号绘制的剖面图 Fig. 13 The protile wasmade by scale trans for mationfor detecting target signal of stochastic resonance |
从图 12中可以看出,在浅层反演中,测深100~300m 深,测点50 到200 处有低阻体异常,因此浅层信号反演效果较好,基本与实际地质对应.但对测点号50到100,230到250处地下深500~800m 的低阻体无任何显示,证明此时该算法由于人文电磁干扰无法得到深层微弱信号,因此无法反演该处的地质信息.
从图 13中可以看出该测线上测点80至240所在位置地下100~200m 之间有低阻异常,测点50~100和230~250所在位置地下500~800m 之间有低阻异常.剖面结果说明采用本文介绍的方法检测出的二次场值能较为准确地反映实际地质构造,为精确地质反演提供了理论保证和技术支持.
4 结论瞬变电磁仪的晚期信号表征一般非常微弱,这对信号特征的提取提出了更高的要求.传统的微弱信号检测在抑制噪声的同时,被检测信号也受到了抑制或损失,对于这种极限情况的微弱信号(-50dB),基本上无法提取出末端目标信号.随机共振存在着噪声能量向信号能量转移的机制,但仅在低频或已知信号为高频频率的情况下有高强度的信号输出.本文利用尺度变换改进随机共振系统,可使高频未知信号经过连续的尺度变换后,再通过非线性双稳系统发生共振,依次提取出共振频率后反变换即可得到原始信号的所有频率,再叠加即可得到原始的晚期瞬变电磁信号.所提出的尺度变换的随机共振方法,有效地解决了传统晚期瞬变电磁信号降噪方法对特征信号的保留能力不足、数据采集量大、处理速度慢的缺陷,实现了在较宽频率范围内从强噪声中检测瞬变电磁微弱信号,能使晚期的瞬变电磁信号末端特征突出、明显,使探测深度加大,探测精度提高,且效果稳定.
| [1] | 于景邨, 刘志新, 刘树才, 等. 深部采场突水构造矿井瞬变电磁法探查理论及应用. 煤炭学报 , 2007, 32(8): 818–821. Yu J C, Liu Z X, Liu S C, et al. Theoretical analysis of mine transient electromagnetic method and its application in detecting water burst structures in deep coal stope. Journal of China Coal Society (in Chinese) , 2007, 32(8): 818-821. |
| [2] | 王华军. 时间域瞬变电磁法全区视电阻率的平移算法. 地球物理学报 , 2008, 51(6): 1936–1942. Wang H J. Time domain transient electromagnetism all time apparent receptivity translation algorithm. Chinese J. Geophys. (in Chinese) , 2008, 51(6): 1936-1942. |
| [3] | 薛国强, 李貅. 瞬变电磁隧道超前预报成像技术. 地球物理学报 , 2008, 51(3): 894–900. Xue G Q, Li X. The technology of TEM tunnel prediction imaging. Chinese J. Geophys. (in Chinese) , 2008, 51(3): 894-900. |
| [4] | 牛之琏. 时间域电磁法原理. 长沙: 中南大学出版社, 2007 : 96 -106. Niu Z L. Principles of Time Domain Electromagnetic Method (in Chinese). Changsha: Central South University Press, 2007 : 96 -106. |
| [5] | 郭文波, 李貅, 薛国强, 等. 瞬变电磁快速成像解释系统研究. 地球物理学报 , 2005, 48(6): 1400–1405. Guo W B, Li X, Xue G Q, et al. A study of the interpretation system for TEM tomography. Chinese J. Geophys. (in Chinese) , 2005, 48(6): 1400-1405. |
| [6] | 闫述, 陈明生. 瞬变电磁场资料的联合时-频分析解释. 地球物理学报 , 2005, 48(1): 203–208. Yan S, Chen M S. Interpretation of transient electromagnetic field data using joint time-frequency analysis. Chinese J. Geophys. (in Chinese) , 2005, 48(1): 203-208. |
| [7] | Lars Nielsen, Niels O J, Peter Gelting. Mapping of the freshwater lens in a coastal aquifer on the Keta Barrier (Ghana) by transient electromagnetic soundings. Journal of Applied Geophysics , 2007, 62(1): 1-15. DOI:10.1016/j.jappgeo.2006.07.002 |
| [8] | Flores C, Peralta-Ortega S A. Induced polarization with in-loop transient electromagnetic soundings: A case study of mineral discrimination at El Arco porphyry copper, Mexico. Journal of Applied Geophysics , 2009, 68(3): 423-436. DOI:10.1016/j.jappgeo.2009.03.009 |
| [9] | Zubia I, Ostolaza X, Susperregui A, et al. Complete wind farm electromagnetic transient modeling for grid integration studies. Energy Conversion and Management , 2009, 50(3): 600-610. DOI:10.1016/j.enconman.2008.10.024 |
| [10] | Kim S K, Jeon J H, Cho C H, et al. Modeling and simulation of a grid-connected PV generation system for electromagnetic transient analysis. Solar Energy , 2009, 83(5): 664-678. DOI:10.1016/j.solener.2008.10.020 |
| [11] | Hobara Y, Walker S N, Dunlop M, et al. Mode identification of terrestrial ULF waves observed by Cluster: A case study. Planetary and Space Science , 2007, 55(15): 2257-2260. DOI:10.1016/j.pss.2007.05.020 |
| [12] | Chen H, Varshney P K, Michels J H. Noise enhanced parameter estimation. IEEE Transactions on Signal Processing , 2008, 56(10): 5074-5081. DOI:10.1109/TSP.2008.928508 |
| [13] | Benzi R, Srutera A, Vulpiani A. The mechanism of stochastic resonance. J Phys A , 1981, 14(11): 453-457. DOI:10.1088/0305-4470/14/11/006 |
| [14] | Hartmann F, Hartmann D, Kowalzik P, et al. Stochastic resonance in a nonsocial Y-branch switch. Applied Physics Letters , 2010, 96(17): 7210-7216. |
| [15] | Sowers R B. Averaging of stochastic flows: Twist maps and escape from resonance. Stochastic Processes and their Applications , 2009, 119(10): 3549-3582. DOI:10.1016/j.spa.2009.04.004 |
| [16] | Aihara T, Kitajo K, Nozaki D, et al. Internal noise determines external stochastic resonance in visual perception. Vision Research , 2008, 48(14): 1569-1573. DOI:10.1016/j.visres.2008.04.022 |
| [17] | Mirko L, Massimiliano I, Fronzoni L, et al. The rate matching effect: A hidden property of a periodic stochastic resonance. Physics Letters A , 2008, 372(15): 2608-2913. DOI:10.1016/j.physleta.2007.11.070 |
| [18] | 郭立敏, 徐伟, 阮春蕾, 等. 二值噪声驱动下二阶线性系统的随机共振. 物理学报 , 2008, 57(12): 7483–7486. Guo L M, Xu W, Ruan C L, et al. Stochastic resonance for dichotomous noise in a second derivative linear system. Acta Physica Sinica (in Chinese) , 2008, 57(12): 7483-7486. |
| [19] | 陈敏, 胡茑庆, 秦国军, 等. 参数调节随机共振在机械系统早期故障检测中的应用. 机械工程学报 , 2009, 45(4): 131–135. Chen M Hu N Q, Qin G J, et al. Application of parameter-tuning stochastic resonance for detecting early mechanical faults. Journal of Mechanical Engineering (in Chinese) , 2009, 45(4): 131-135. DOI:10.3901/JME.2009.04.131 |
 2011, Vol. 54
2011, Vol. 54