2. 中国国土资源航空物探遥感中心对地观测技术工程实验室,北京 100083
2. Laboratory of Earth Observation Technology, China Aero Geophysical Survey and Remote Sensing Center for Land and Resources, Beijing 100083, China
作为最早应用的地球物理方法,重磁勘探具有快速、经济、能大面积探测等特点.航空磁测和航空重力测量则继承了其传统优势,具有更加快速、覆盖广阔、适宜海陆联测等突出优点,因而得到广泛应用.我国航空地球物理勘探始于1953 年,经过50余年的发展,航空物探测量从理论方法、仪器研发、数据采集与处理等已形成具有中国特色的完整的技术体系,具备了从海洋到高原全区域覆盖的作业能力[1].无论是磁场还是重力场在研究地质目标体的横向不均匀,特别是地质目标体边缘位置时,具有独特优势;对于地质构造的演化形迹,无论出露于地表还是隐伏于地下,多数情况能在航空重力和航磁图件中有所反映.近年来,国内外发展了一系列基于重磁位场梯度及其高阶导数进行位场增强与边缘识别的方法技术,相关研究发展也十分迅速[2].但在航空重力和航空磁测实际资料解释中,这类技术方法尚无法完全应用,特别是地形切割剧烈的地区.有时受飞行条件的限制,航测中相邻测线间飞行高度可能相差很大,航空物探资料上表现为沿测线方向的条带干扰---即测线间的水平差异;此外,仪器的零点漂移、日变改正等也能引起水平差异.通过切割线飞行测量虽能够控制一定的低频干扰,但中高山区测线与切割线交点的高度差有时很大,切割线调平效果并不理想,微调平处理[3]也无法完全消除此类现象.正因如此,目前航磁解释中通常仅应用化极、向上延拓和垂向导数计算等处理方法.由于测线水平差异等问题,有时甚至无法计算垂向导数.目前,基于梯度及其高阶导数的位场增强与边缘识别等解释方法还较少用于航空重磁资料解释.
针对重磁位场梯度及其高阶导数进行位场增强与边缘识别这类技术方法难以实际应用的突出问题,我们根据重磁场梯度满足希尔伯特变换的性质,提出了位场直接解析信号的概念.在阐述重磁场直接希尔伯特变换含义的基础上,给出了基于直接解析信号概念对位场数据进行增强的处理方法,用以解决噪声干扰和测线水平差异等问题,这对于航空磁测和航空重力资料处理和解释具有实际意义.
2 位场希尔伯特变换Nabighian[4, 5] 通过引入解析信号(AnalyticSignal)的概念,提出二维情况下重磁场水平梯度和垂向梯度满足希尔伯特变换关系,构成解析信号,其解析信号模---解析信号包络与磁化方向无关.1984年Nabighian[6]将解析信号理论扩展至三维位场,提出重磁场水平两个方向上的梯度与垂向梯度间转换的希尔伯特变换关系.1992年Roest等[7]提出三维解析信号,认为三维解析信号的幅度---总梯度模(TotalGradient)不受磁化方向影响,能够反映场源位置;Qin[8]也提出了类似观点,声称磁化方向不影响总梯度模的形态.Agarwal[9] 和管志宁[10~12]等则分别就总梯度模不受磁化方向影响等结论提出了质疑,长期以来关于对总梯度模的认识一直存在偏差,直至Haney等[13]和Li[14]撰文,解析信号理论渐趋清晰.
实信号f的解析信号AS被定义为
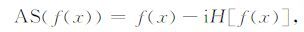
|
(1) |
其中i2=-1,H[]表示希尔伯特变换.根据Nabighian等的推导,位场解析信号为
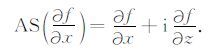
|
(2) |
Nabighian[4, 5]借鉴了解析信号[15]的概念,根据定义上述解析信号实际上是重磁场梯度的解析信号,而非重磁场的解析信号.其后,Nabighian将位场的希尔伯特变换推广至二维,Roest按照式(2)的形式,定义了三维解析信号:
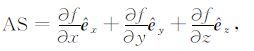
|
(3) |
其中êx,êy,êz分别是x,y,z方向的单位矢量.同样,Roest根据二维希尔伯特变换给出三维解析信号的定义也应是重磁场梯度的解析信号,而非重磁场的直接解析信号.事实上,几乎所有的位场研究都在借用解析信号概念,实际使用的则是重力场或磁场梯度的解析信号,并没有真正使用希尔伯特变换计算重磁场的解析信号.希尔伯特变换不同于其他位场转换,不改变信号的幅度,仅改变信号的相位,是一种绝对稳定的变换.Nabighian扩展二维希尔伯特变换时,一个重要的应用就在于通过希尔伯特变换将空间域中换算的水平梯度转换为垂向梯度,这种垂向梯度计算方法极具优势[16].但目前多数位场增强与边缘识别中采用的均是重磁场梯度及其高阶导数计算方法,利用的是梯度解析信号的幅度或相位,由于梯度计算本身的不稳定,造成难以实际应用.通过上述分析,我们定义位场f直接的解析信号:
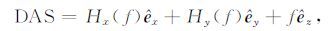
|
(4) |
其中Hx与Hy分别代表二维希尔伯特变换在x和y方向上的分量;这与式(3)梯度数据的解析信号相类似,能够用于位场增强与边缘识别等方法.但却不同于现有基于梯度数据的解析信号解释方法,我们称其为位场的直接解析信号(Direct Analytic Signal)或位场直接希尔伯特变换方法(Direct Hilbert Transform Method).
二维希尔伯特变换可以在频率中直接计算,其傅里叶域变换因子为[6, 16]
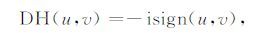
|
(5) |
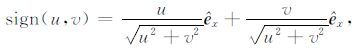
|
(6) |
其中,i2 =-1,u、v分别是x和y方向上的波数.式(4)中解析信号的分量可以表示为
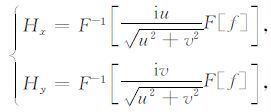
|
(7) |
其中F[],F-1[]分别表示傅里叶变换及其逆变换.
对于重力异常gz,其解析信号为
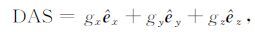
|
(8) |
用以表征万有引力异常矢量.而对于航空磁测中测量的磁场总强度,其TMI 异常(Total Magnetic Intensity, 总场磁异常)的解析信号为
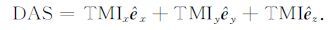
|
(9) |
根据已有对解析信号的认识,TMI异常的解析信号仍受磁化方向影响,这点不同于二维情况,二维TMI异常的解析信号模与磁化方向完全无关;但化极后TMI的解析信号则具有实际物理含义,表征化极后的磁异常矢量.
3 位场增强技术根据前面提出的位场直接解析信号,可知重磁测量参量gz或TMI化极异常的直接解析信号与异常矢量是等效的,可以借助已有的矢量解释方法对其进行解释.由于gz或TMI的直接解析信号与目前实际使用的梯度解析信号均满足希尔伯特变换关系,因而用于梯度进行位场增强与边缘识别的方法均适用于直接解析信号.下面将介绍基于二维希尔伯特变换改进的重磁位场增强方法.
3.1 解析信号模Roest等定义的解析信号[7],其重要应用就是计算总梯度模,前面阐述了直接解析信号的物理意义,说明用解析信号模替代总梯度模具有实际意义.直接解析信号模的定义为
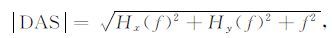
|
(10) |
其中f是可测量的位场gz或TMI,只不过化极后TMI的解析信号模更具物理意义.
3.2 水平分量模水平梯度模在位场资料处理中被广泛应用,如马宗晋等[17]采用水平梯度模对布格重力异常中反映的中国大地构造信息进行判读和解释.我们依据直接解析信号来定义解析信号的水平分量模:
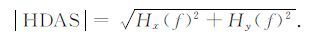
|
(11) |
解析信号的水平分量模表征重力异常或化极异常水平分量的幅度,通过判别水平分量大小达到地质边界识别的效果.对于通常的TMI异常,根据已有对水平梯度模的认识,解析信号的水平分量模在一定程度上仍可以反映地质边界.
3.3 改进Tilt angle解析信号的应用不仅限于模量---总梯度模,其相位也具有表征边界的能力.Miller和Singh 应用解析信号相位提出了Tilt angle[18],根据直接解析信号,我们提出改进Tilt angle:
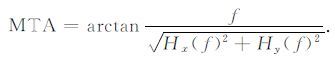
|
(12) |
Tilt angle本身具有一定的物理意义,例如Thurston和Smith提出的磁源成像SPI(TM)方法中就使用了Tilt angle[19],这一方面研究及应用发展很快;但目前改进的Tilt angle还仅能作为解析信号相位对位场进行增强,其物理意义仍有待深入研究.
3.4 改进Tilt angleWijns等利用Roest等定义的解析信号,提出了Thet amap或Theta angle[20].我们则根据直接解析信号来改进Thet amap:
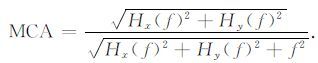
|
(13) |
与Tilt angle相比,Thet amap在理论上可能并不具备优势;Li指出Thet amap 中由于缺少垂向梯度,尽管与Tilt angle一定程度上是等价的,但因水平梯度模无负号的原因会损失部分位场信息[21],该论断仍适用于改进Thet amap.
根据解析信号原理并结合已有位场梯度参量增强和解释方法,我们分别从解析信号的幅度和相位两个方面提出基于直接解析信号的位场增强方法,初步提出了直接解析信号模和水平分量模、改进Tilt angle与改进Thet amap四种处理方法.目前,借助位场梯度或解析信号进行位场增强的这类方法发展很快,国内也开展了相关的应用[22~24],Cooper[25]最近又提出了相类似的方法;但无论这类技术如何发展,只要位场计算中采用了三个方向上的梯度分量,就可以利用直接解析信号的三个分量替代,二者具有等价关系:
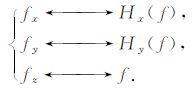
|
(14) |
上述等价关系是根据解析信号的定义及其分量间满足二维希尔伯特变换关系类比得到的,并且重力异常和磁力化极异常的直接解析信号具有实际地球物理含义.应用上述关系进行位场解释的优势在于希尔伯特变换不会放大位场数据中的噪声干扰,能够用于实际飞行条件下获取的航空重磁资料,不会因为测线水平等干扰而无法成图.理论模型和实际资料处理的对比中这一优势十分显著.
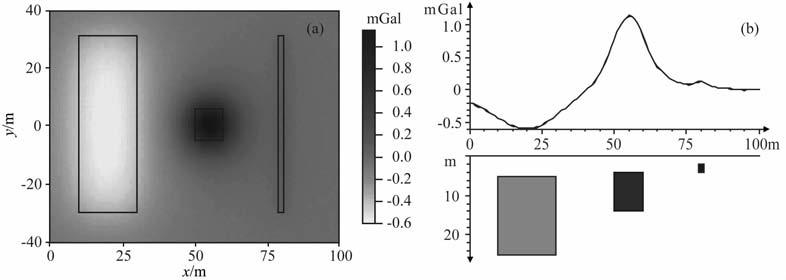
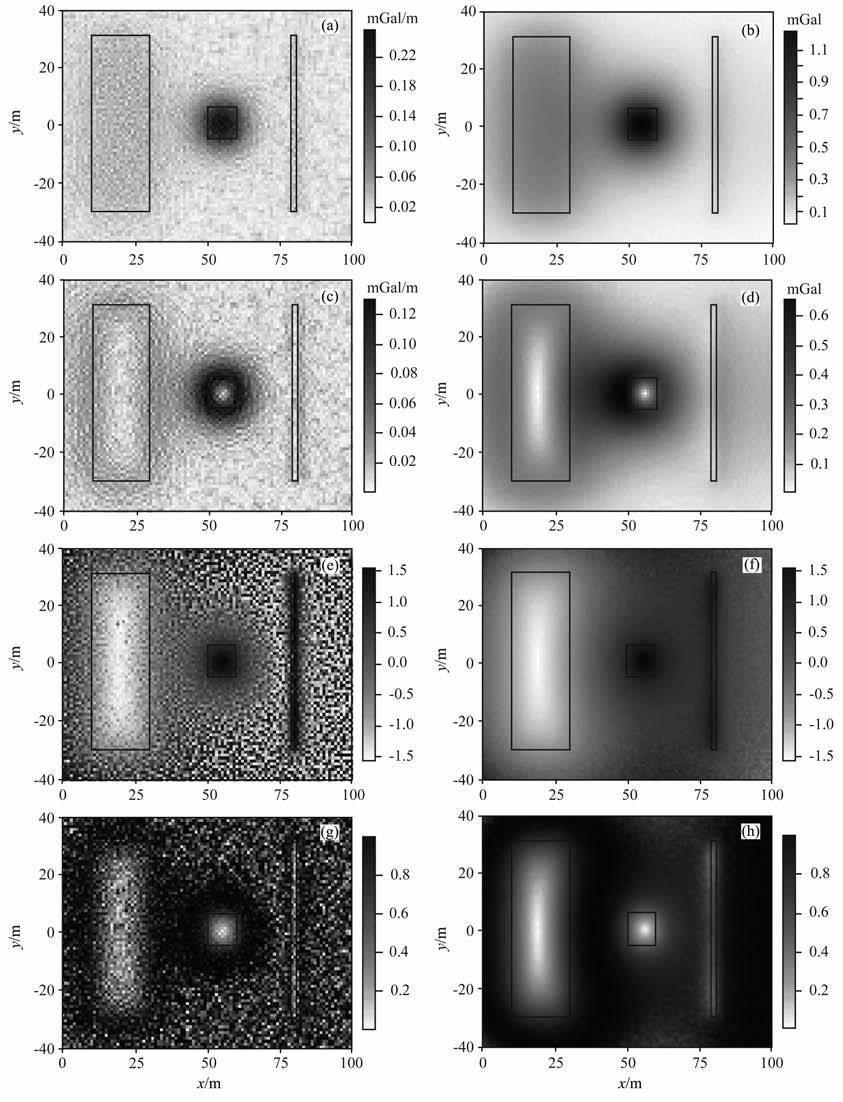
4 模型计算与对比为了检验基于希尔伯特变换的位场解释方法,我们采用了含有噪声的组合重力模型对位场增强效果进行检验.图 1给出了加入高斯白噪声的重力异常以及过异常中心的剖面图,场源的边界用黑色线框标注,场源埋深情况如图 1b所示.图 1中加入标准差为0.005mGal的高斯白噪声,噪声的最大幅度不超过0.018mGal;由于噪声干扰很小,小于0.003mGal的噪声占75%以上,图 1a几乎看不出任何噪声干扰,图 1b剖面图也显示出加入噪声后的异常曲线与理论模型曲线基本完全重合.我们对图 1a给出的网格数据(网格间距1m×1 m)分别进行基于梯度计算的位场增强和基于希尔伯特变换的位场增强,图 2给出了对比结果.图 2a、图 2c、图 2e、图 2g分别为图 1a 数据对应的总梯度模、水平梯度模、Tilt angle和Thet amap, 图 2b、图 2d、图 2f、图 2h则是与之对应的直接解析信号模、水平分量模、改进Tilt angle和改进Thet amap.可以看出,处理数据中虽然仅含有微弱的噪声,转换后总梯度模和水平梯度模的噪声水平就明显增大,Tilt angle和Thet amap将噪声放大到几乎湮灭地质信号的程度,而基于位场直接解析信号参量的图件,其噪声放大水平则并不显著;解析信号模(图 2b)和水平分量模(图 2d)的噪声水平与原始数据相当,基本不受干扰;改进的Tilt angle及Thet amap 对噪声则略有放大,但对比Tilt angle和Thet amap其抗噪声干扰能力仍十分显著.由于希尔伯特变换的频率域因子幅度均不大于1,不会像梯度算子那样对噪声干扰放大,尽管较梯度运算给出的边界略平缓,但与采用梯度及高阶导数增强位场的方法相比,实际应用中的限制大为减少,适用范围更广.
|
图 1 重力异常模型 (a)为加入高斯白噪声的重力异常,黑色线框表示模型边界;(b)组合模型垂直剖面. Fig. 1 Synthetic example (a) Noise-corrupted gravity anomalies, there are three bodies in the model, and their outlines are superimposed on the data; (b) The verticai profile view of models. |
|
图 2 基于梯度解析信号的位场增强与直接解析信号位场增强 (a)总梯度模;(b)解析信号模;(c)水平梯度模;(d)水平分量模;(e)Tilt angle;(f)改进Tilt angle;(g)Thet amap;(h)改进Thet amap. Fig. 2 Edge enhancement of potential field data by analytic signal and direct analytic signal (a) Analytic signal of the data; (b) Direct analytic signal of the data; (c) Total horizontal derivative; (c) Horizontal amplitudeof direct analytic signal;(e) Tilt angle; (f) Improved Tilt angle; (g) Theta map; (h) Improved Theta map. |
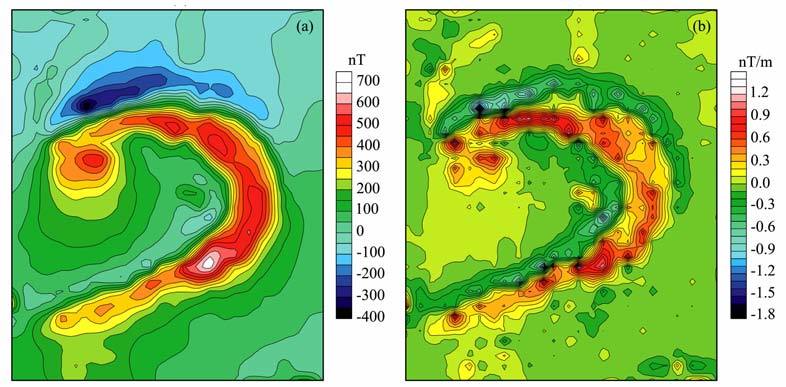
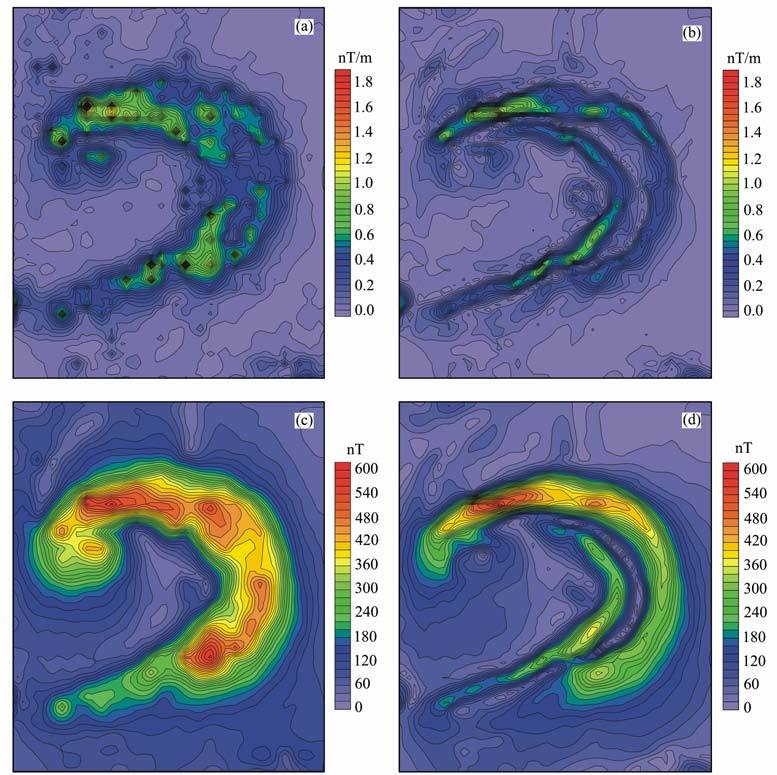
为了对比实际资料处理效果,我们选取了内蒙古布敦花地区某航磁异常资料进行处理,该异常曾使用多种方法进行反演处理[10, 26~28],地下岩体的赋存状态已知,便于分析对比.图 3a给出了异常的等值线图,可以看出异常呈马蹄形展布,主体正异常北侧伴生有负异常.图 3a等值线图并没有显示出明显的测线水平,但由于资料系数字化而来具有一定的串珠状特征,这一点在图 3b转换后的垂向梯度尤为明显.我们先就总梯度模、水平梯度模与直接解析信号的模及水平分量模进行对比;图 4a和图 4b分别为该异常的总梯度模和水平梯度模,图 4c和图 4d分别为图 3a直接解析信号的总模量及水平分量模.由于转换后的垂向梯度(图 3b)表现出一定的串珠状特征,计算的总梯度模(图 4a)也会有所反映,水平梯度模(图 4b)略有改善;值得注意的是,无论是总梯度模还是水平梯度模,其异常幅度差异变化很大,更易受到浅部异常及噪声的干扰.相对而言,直接解析信号模(图 4c)及直接解析信号水平分量模(图 4d)表现的异常同场源具有较好的对应关系,其异常幅度与原航磁异常(图 3a)相当且使用相同的物理量纲,其中图 4c的直接解析信号模类似于航磁化极图,部分消除了斜磁化影响,异常幅度大体反映了场源的相对磁性强度;图 4c表现的这一特点对航磁异常解释十分有利.
|
图 3 某航磁异常(a)及转换的垂向梯度(b) Fig. 3 Digital aeromagnetic data (a) and its vertical gradient (b) |
|
图 4 总梯度模(a)、水平梯度模(b)以及直接解析信号模(c)和水平分量模(d) Fig. 4 Total gradient map (a) ,horizontal gradient map (b) ,amplitude ofdirect analytical signal (c) and its horizontal amplitude (d) |
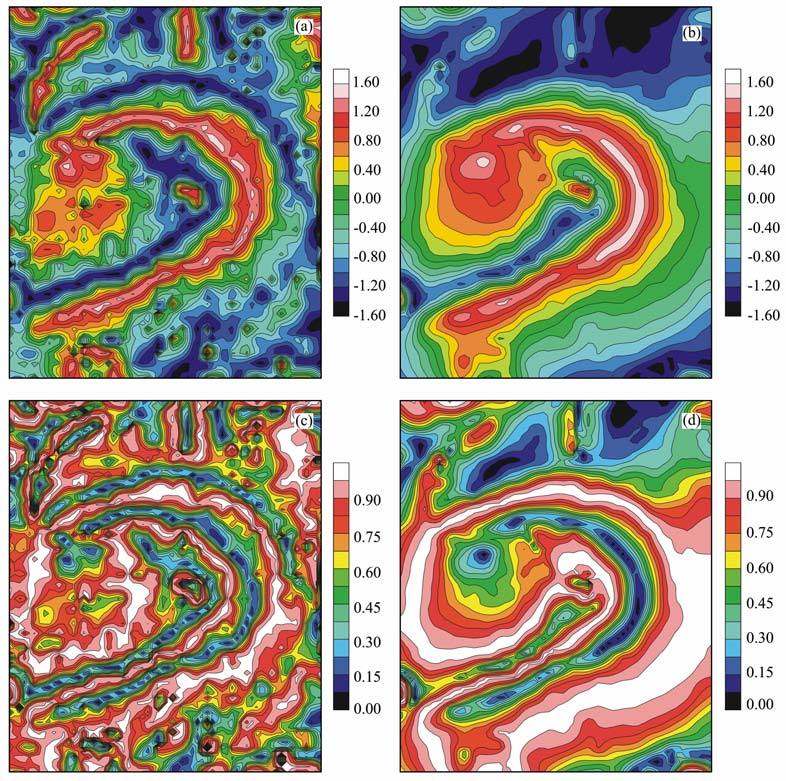
我们对改进的Tilt angle和Thet amap也进行了对比,图 5a和图 5b分别为Tilt angle及其改进,图 5c和图 5d分别为Thet amap及其改进.Tilt angle和Thet amap及其改进的Tilt angle和Thet amap表示的均为矢量相位信息,不同于矢量模量信息,Tilt angle及其改进与Thet amap及其改进分别具有相同的物理量纲,表达异常的形式完全类似,异常图像接近,具体异常的细节也较一致.但不难发现,改进的Tilt angle和Thet amap具有更强的抗噪声干扰能力,受浅部异常及噪声干扰影响相对较少,对场源整体的分辨和刻画能力较强.由于二维希尔伯特变换---直接解析信号解释方法均是在频率域中进行的,资料处理与传统位场转换方法无异,只是频率域算子不同,完全可以处理区域性航空重磁资料,限于篇幅本文不再对大数据量网格和含假值网格资料的处理效果进行展示.
|
图 5 Tilt angle(a)及其改进Tilt angle(b)与Thet amap(c)及其改进Thet amap(d) Fig. 5 Tilt angle (a) and the improved one (b),and Theta map (c) and the improved map(d) |
在分析解析信号概念的基础上,指出重磁场解析信号实际上是重磁场梯度的解析信号,通过二维希尔伯特变换提出重磁场直接解析信号概念,阐述了重力异常及化极异常的直接希尔伯特变换---直接解析信号的含义.针对传统基于解析信号进行位场增强与边缘识别难以应用于实际资料这一突出问题,给出了基于直接解析信号对位场数据进行增强的处理方法,用以解决噪声干扰和测线水平差异等问题.理论模型和实际资料表明重磁场二维希尔伯特变换---直接解析信号解释方法一定程度上能解决噪声干扰问题,其相应的解释图件对分辨和刻画场源具有较好的辅助效果,能够用于区域性航空重力和航磁资料处理和解释,是一种可以实用的位场增强与边缘识别方法.
| [1] | 熊盛青. 我国航空重磁勘探技术现状与发展趋势. 地球物理学进展 , 2009, 24(1): 113–117. Xiong S Q. The present situation and development of airborne gravity and magnetic survey techniques in China. Progress in Geophysics (in Chinese) , 2009, 24(1): 113-117. |
| [2] | 王万银, 邱之云, 杨永, 等. 位场边缘识别方法研究进展. 地球物理学进展 , 2010, 25(1): 196–210. Wang W Y, Qiu Z Y, Yang Y, et al. Some advances in the edge recognition of the potential field. Progress in Geophysics (in Chinese) , 2010, 25(1): 196-210. |
| [3] | Minty B R S. Simple micro-levelling for aeromagnetic data. Explor. Geophys , 1991, 22(4): 591-592. |
| [4] | Nabighian M N. The analytic signal of two-dimensional magnetic bodies with polygonal cross-section: Its properties and use for automated anomaly interpretation. Geophysics , 1972, 37(3): 507-517. DOI:10.1190/1.1440276 |
| [5] | Nabighian M N. Additional comments on the analytic signal of two-dimensional magnetic bodies with polygonal cross-section. Geophysics , 1974, 39(1): 85-92. DOI:10.1190/1.1440416 |
| [6] | Nabighian M N. Toward a three-dimensional automatic interpretation of potential field data via generalized Hilbert transforms: Fundamental relations. Geophysics , 1984, 49(6): 780-786. DOI:10.1190/1.1441706 |
| [7] | Roest W R, Verhoef J, Pilkington M. Magnetic interpretation using the 3-D analytic signal. Geophysics , 1992, 57(1): 116-125. DOI:10.1190/1.1443174 |
| [8] | Qin S. An analytic signal approach to the interpretation of total field magnetic anomalies. Geophys. Prospect , 1994, 42(6): 665-675. |
| [9] | Agarwal B N P, Shaw R K. Comment on 'An analytic signal approach to the interpretation of total field magnetic anomalies' by Shuang Qin. Geophys. Prospect , 1996, 44(5): 911-914. |
| [10] | 管志宁, 姚长利. 倾斜板体磁异常总梯度模反演方法. 地球科学——中国地质大学学报 , 1997, 22(1): 81–85. Guan Z N, Yao C L. Inversion of the total gradient modulus of magnetic anomaly due to dipping dike. Earth Sci.-J. China Univ. Geosci. (in Chinese) , 1997, 22(1): 81-85. |
| [11] | Huang L P, Guan Z N, Yao C L. Comment on: 'An analytic signal approach to the interpretation of total field magnetic anomalies' by Shuang Qin. Geophys. Prospect , 1997, 45(5): 879-881. |
| [12] | Huang L P, Guan Z N. Discussion on: "Magnetic interpretation using the 3-D analytic signal". Geophysics , 1998, 63(2): 667-670. DOI:10.1190/1.1444366 |
| [13] | Haney M, Johnston C, Li Y G, et al. Envelopes of 2D and 3D magnetic data and their relationship to the analytic signal: Preliminary results. In: 73rd Ann. Internat. Mtg. Soc. Expl. Geophys., Expanded Abstracts. 2003. 596~599 |
| [14] | Li X. Understanding 3D analytic signal amplitude. Geophysics , 2006, 71(2): L13-L16. DOI:10.1190/1.2184367 |
| [15] | Bracewell R N. The Fourier Transform and Its Applications, Second Edition. New York: McGraw-Hill, 1986 . |
| [16] | Moon W M, Ushah A, Singh V, et al. Application of 2-D Hilbert transform in geophysical imaging with potential field data. IEEE Trans. Geosci. Remote Sensing , 1988, 26(5): 502-510. |
| [17] | 马宗晋, 高祥林, 宋正范. 中国布格重力异常水平梯度图的判读和构造解释. 地球物理学报 , 2006, 49(1): 106–114. Ma Z J, Gao X L, Song Z F. Analysis and tectonic interpretation to the horizontal-gradient map calculated from Bouguer gravity data in the China mainland. Chinese J. Geophys. (in Chinese) , 2006, 49(1): 106-114. |
| [18] | Miller H G, Singh V. Potential field tilt—a new concept for location of potential field sources. J. Appl. Geophys , 1994, 32(2-3): 213-217. |
| [19] | Thurston J B, Smith R S. Automatic conversion of magnetic data to depth, dip, and susceptibility contrast using the SPI (TM) method. Geophysics , 1997, 62(3): 807-813. DOI:10.1190/1.1444190 |
| [20] | Wijns C, Perez C, Kowalczyk P. Theta map: Edge detection in magnetic data. Geophysics , 2005, 70(4): L39-L43. DOI:10.1190/1.1988184 |
| [21] | Li X. On "Theta map: Edge detection in magnetic data". Geophysics , 2006, 71(3): X11. DOI:10.1190/1.2194525 |
| [22] | 王想, 李桐林. Tilt梯度及其水平导数提取重磁源边界位置. 地球物理学进展 , 2004, 19(3): 625–630. Wang X, Li T L. Locating the boundaries of magnetic or gravity sources with Tdr and Tdr -Thdr methods. Progress in Geophysics (in Chinese) , 2004, 19(3): 625-630. |
| [23] | 刘金兰, 李庆春, 赵斌. 位场场源边界识别新技术及其在山西古构造带与断裂探测中的应用研究. 工程地质学报 , 2007, 15(4): 569–574. Liu J L, Li Q C, Zhao B. New detection techniques of geologic boundaries using potential-field data and its application in the Shanxi paleo-structure zone and faults. Journal of Engineering Geology (in Chinese) , 2007, 15(4): 569-574. |
| [24] | 戴明刚, 曲寿利. 位场梯度模法及其在碳酸盐岩地区断裂识别中的应用. 地球物理学进展 , 2009, 24(3): 951–958. Dai M G, Qu S L. Determination of faults using gradient modules of potential field anomalies and its application to carbonate rock area of South China. Progress in Geophysics (in Chinese) , 2009, 24(3): 951-958. |
| [25] | Cooper G R J. Balancing images of potential-field data. Geophysics , 2009, 74(3): L17-L20. DOI:10.1190/1.3096615 |
| [26] | 管志宁, 侯俊胜, 黄临平, 等. 重磁异常反演的拟BP神经网络方法及其应用. 地球物理学报 , 1998, 41(2): 242–251. Guan Z N, Hou J S, Huang L P, et al. Inversion of gravity and magnetic anomalies using pseduo-BP neural network method and its application. Chinese J. Geophys. (Acta Geophysica Sinica) (in Chinese) , 1998, 41(2): 242-251. |
| [27] | 田黔宁, 吴文鹂, 管志宁. 任意形状重磁异常三度体人机联作反演. 物探化探计算技术 , 2001, 23(2): 125–129. Tian Q N, Wu W L, Guan Z N. Interaction inversion for 3D gravity and magnetic anomalous bodies with arbitrary shaped. Computing Techniques for Geophysical and Geochemical Exploration (in Chinese) , 2001, 23(2): 125-129. |
| [28] | 姚长利, 郑元满, 张聿文. 重磁异常三维物性反演随机子域法方法技术. 地球物理学报 , 2007, 50(5): 1576–1583. Yao C L, Zheng Y M, Zhang Y W. 3-D gravity and magnetic inversion for physical properties using stochastic subspaces. Chinese J. Geophys. (in Chinese) , 2007, 50(5): 1576-1583. |
 2011, Vol. 54
2011, Vol. 54

