2. 中国石化胜利油田分公司勘探项目管理部,东营 257000;
3. 北京吉星吉达科技有限公司,北京 100029
2. SINOPEC Shengli Oilfield Company, Exploration Project Management, Dongying 257000, China;
3. Beijing Geostar Science and Technology Co. Ltd, Beijing 100029, China
随着地震勘探技术的不断发展,油气地震勘探的重点正转向起伏地表条件和复杂地质条件的区域,如山地、滩海和沼泽地区等,这对地震勘探工作及资料处理提出了新的挑战.传统地震成像方法在复杂地表、复杂构造地区主要存在两方面的问题:一是地表起伏大,表层速度结构十分复杂;二是地下构造复杂,如褶皱强烈、断层发育、构造陡峻、地层产状变化大等.这种双复杂结构使得传统地震成像方法在这类地区难以准确成像.
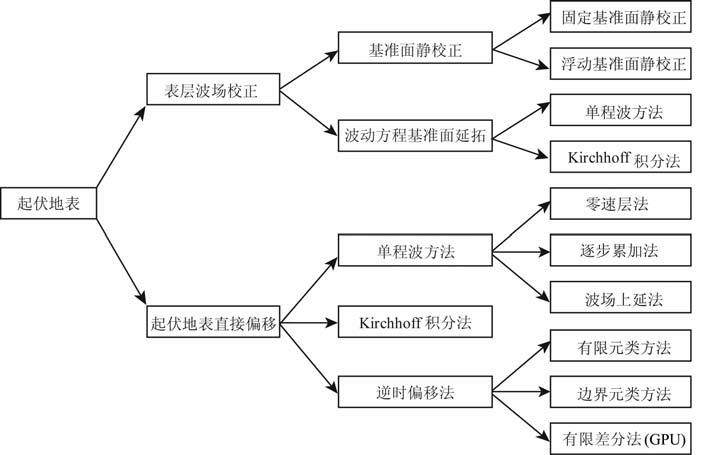
图 1 给出了起伏地表地震资料处理的不同方案,起伏地表地区地震资料成像主要采用两种方法:一种是先进行表层波场校正,再偏移成像,该法在实际生产中占主导地位;另一种是直接从起伏地表进行深度域的偏移成像.表层波场校正一直是实际地震资料处理中一项关键处理技术,通常采用高程基准面静校正将地震数据校正到固定基准面或者浮动基准面上的办法解决地形起伏的影响.在地形平缓的地区,近地表速度比地下速度慢很多,且射线路径出射角较小,采用上述校正方法比较合适,但在复杂地表和复杂地下构造的区域,简单的校正可能会扭曲波场,降低地震成像的质量,此时常规处理不能产生正确的成像.波动方程基准面延拓方法为表层波场校正提供了一种更精确的技术手段.只要能够得到比较准确的近地表速度模型,以“波动方程基准面延拓"替换常规“时移静校正",对提高山前带复杂构造成像精度非常重要.Berryhill[1]首先提出波动方程基准面校正的概念,随后,他又将这个思路扩展到叠前[2, 3].基于这个思路,Yilmaz和Lucas[4],Faye等[5],Ellis和kitchenside[6],Schneider等[7],Bevc[8],YangKai等[9, 10]先后就波动方程基准面校正并结合层替换做了许多有益的尝试,使很多实际问题在某种程度上得到解决.
|
图 1 起伏地表地震数据处理方法 Fig. 1 The processing method of seismic data from rugged topography |
直接从起伏地表进行深度域偏移成像的方法,将野外静校正隐含地包括在其中,这种校正不但包含了走时的纵向分量,同时还包含了走时的横向分量,因此,基于起伏地表的叠前深度偏移可以同时解决上述提到的复杂地表和复杂地下构造这种地质上的双重复杂性问题.
接下来的问题是选择何种偏移算法进行起伏地表的直接偏移.Kirchhoff积分法简便、高效,适应任意观测方式,且易于对局部目标成像.Wiggins[11]证明了Kirchhoff偏移在起伏地表条件下的适应性.射线追踪法主要考虑地震波传播的运动学特征,可以灵活地处理起伏的地表条件,所得的地震波的传播时间比较准确,但Kirchhoff积分法是一种高频近似,不能对复杂波场中的焦散、干涉现象进行很好的处理,在强横向非均匀介质中成像精度不高,计算结果很难保持地震波的动力学特征,而且面对复杂的地质构造会出现盲区.与Kirchhoff偏移法相比,起伏地表单程波波动方程叠前深度偏移法对复杂地区构造成像精度高,且能处理多波至问题,对陡倾界面、断层和断面的刻画更清晰.为了把单程波波动方程偏移推广应用于起伏观测面地区,Reshef[12]基于波场可以叠加的思路提出了“逐步累加"波场外推的思想,可以从任意非水平面进行波场延拓的偏移成像.Beasley等[13]提出了零速层概念,并用于克服复杂地形的影响.这项技术要求在偏移前进行时移静校正,且只适合由绕射项与折射项组成的偏移算子.为了克服上述局限性,何英等[14]提出了一种以波场上延取代零速层时移静校正的波动方程叠前深度偏移方法.本质上,它是波动方程“基准面延拓+ 叠前深度偏移"两步法,只是不需要将炮点向上延拓到水平基准面而已.近年来,随着单程波波动方程数值解法的不断改进,涌现出许多类似的从起伏地表直接正演和偏移的算法.如Geiger等[15],Zhu 等[16],Margrave等[17],MiYanpeng等[18],Shragge等[19],Al-Saleh[20],Xiong等[21],王成祥等[22],程玖兵等[23],田文辉等[24],陈爱萍等[25],杨海生[26].然而,单程波方法同样是一种近似方法,成像角度限制在90°以内,直接求解双程波波动方程的逆时偏移方法突破了成像倾角的限制,是最精确的成像方法.因此,在复杂地表及复杂地下构造这种双重复杂性的地区应该开展起伏地表直接逆时偏移工作.Raiaskaran等[27]利用初至层析成像估算近地表速度,采用相干反演、聚焦分析和反射层析等手段建立深层速度模型,应用双程波有限差分逆时偏移方法实现起伏地表的偏移成像.徐义[28]采用格子法实现起伏地表逆时偏移.
对于起伏地表双程波波动方程的求解,有限差分(FD)方法计算效率高、使用方便,在模拟复杂介质中地震波传播时应用最为广泛,但该方法的一个缺陷就是处理起伏地表比较困难.自由边界处的网格点需要特殊处理,例如,董良国等[29]通过对不同地形起伏情况下自由边界的具体分析,将整个二维空间离散点划分为24类,对每一类自由边界处的网格点选择了合理的表现方式,实现了起伏地表自由边界条件的数值化.然而,这种处理方式意味着大量的逻辑判断,这对GPU 加速是非常不利的.本文采用一种简化的边界处理方式,避免了自由边界网格点细致的分类,从而避免了大量的逻辑判断,利用GPU 实现这种处理方式所需要的额外开销可以忽略不计,数值试验表明了这种处理方式的有效性.
和传统的集群相比,GPU具有计算核心多、硬件成本低、省电、省空间等优点,在石油天然气行业,国际上Hess、CGGVeritas、Chevron、Headwave、Acceleware、Seismiccity等公司和组织都在致力于这方面的研究.中国科学院地质与地球物理研究所刘洪研究员与吉星吉达公司共同合作开发的非对称走时叠前时间偏移GPU 算法[30, 31]已经在胜利、大庆等油田投入生产,效果良好.GPU 已经逐渐成为下一代高性能计算的首选工具.在逆时偏移偏移方面,MicikeviciusP[32]给出了利用GPU 实现高阶有限差分的算法;刘红伟等[33, 34]以及DarrenFoltinek等[35]在利用GPU 实现逆时偏移方面做了有益的尝试.本文的一项主要工作就是围绕利用GPU 加速从起伏地表直接进行逆时偏移展开.
本文首先介绍了单程波起伏地表直接进行偏移的实现方法,在此基础上给出了起伏地表直接逆时偏移的实现方法,边界处理方式,以及利用GPU 加速的实现流程.之后对SEG 起伏地表模型做了测试,通过与单程波方法比较,阐明了逆时偏移方法在起伏地表地区成像方面的优势.
2 起伏地表单程波叠前深度偏移常规偏移方法的基本假设是以水平基准面为边界条件.目前起伏地表单程波深度偏移算法主要采用文献[12]中以色列学者Reshef提出的逐步-累加波场外推的概念,即在采用深度外推时进行基准面校正和偏移.具体做法是将波场从一个水平基准面向下延拓,并在每一个深度步长上将所截得的地形面上的波场值加到延拓的波场中(公式1),这样就可以对起伏地形上的记录进行叠前或叠后偏移.
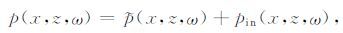
|
(1) |
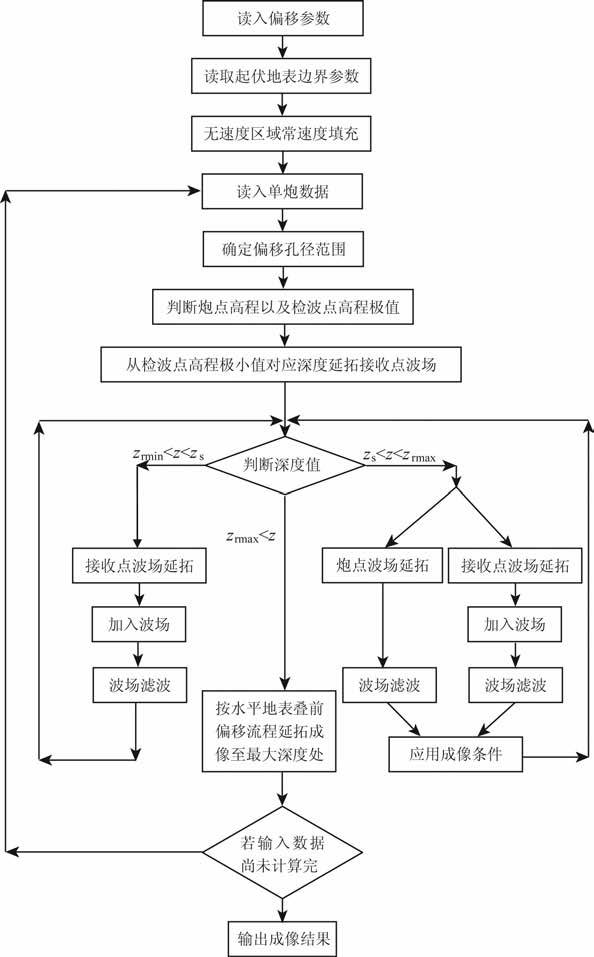
式中,p(x,z,ω)代表深度z上总的波场值,$\tilde{p}$(x,z,ω)代表上一深度的延拓波场值,pin(x,z,ω)代表深度z上所截得的地形面上的波场值.图 2 给出了具体实现起伏地表单程波叠前深度偏移的流程图.首先找到起伏地形的最高点和最低点,将这两点所在水平面之间的部分无速度区域使用常速度填充,该速度应接近地表速度.波场延拓从检波点最大高程对应的深度处开始,在延拓深度小于炮点高程对应的深度值时,只将接收点波场按照公式(1)的方式延拓,这时没有炮点波场,所以不能成像;当延拓深度大于炮点坐标对应的深度且小于检波点最小高程对应的深度时,将炮点波场和检波点波场同时延拓,然后应用成像条件成像.需要注意的是,从波场开始延拓一直到延拓到检波点最小高程对应的深度时,每一次延拓完成之后要按照公式(2)的方式对波场做一次滤波,目的是将起伏地表以上的波场部分置0,这一操作是符合物理实际的.公式(2)中的滤波函数filt(x,z)在起伏地表以上为0,在起伏地表以下为1.当波场延拓到检波点最小高程对应的深度以下时,就可以按照常规的单程波偏移方法进行偏移.
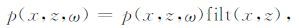
|
(2) |
|
图 2 起伏地表单程波叠前深度偏移流程图 Fig. 2 The flow chart of one-way wave pre-stack depth migration for rugged topography |
从上述起伏地表波场延拓的流程可以看出,这种延拓方法是直接从起伏地表进行的,不需要对波场做时移校正,并且这种延拓方式对波场延拓算子的选择没有限制,本文选取分裂步相移算子[36]实现起伏地表单程波叠前偏移作为起伏地表叠前逆时偏移方法的对比.另外,从单炮偏移流程可以发现,单程波偏移不能对检波点高程最大值与炮点高程之间的地层进行成像,因此,起伏地表叠前单程波偏移方法对近地表地层成像效果较差,这一点在叠前多炮偏移叠加的情况下可以得到一定程度的弥补.
3 起伏地表叠前逆时偏移三维均匀横向各项同性介质声波方程如下:
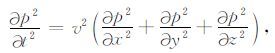
|
(3) |

|
(4) |
式中速度变量v是空间变量的函数,有限差分法逆时偏移利用公式(4)求解上述全波方程,没有成像倾角的限制,是目前最精确的成像手段.叠前逆时偏移技术是解决地震成像问题的有力工具,但逆时偏移面临计算量大、低频成像噪音以及存储量大等三大难题.关于这三个难题的详细介绍见文献[33]和[34].本文主要探讨起伏地表叠前逆时偏移及GPU 加速技术,而这一技术面临的主要难题是如何利用GPU来实现起伏地表自由边界条件.
3.1 起伏地表自由边界条件GPU实现与CPU(中央处理器)不同,GPU 在处理器微观架构上将大部分晶体管用于运算单元(Arithmetic Logical Unit),而只将极少部分用于动态存储,由于大幅度减少了缓存的空间,造成GPU 在逻辑判断、非线性寻址等复杂的逻辑运算的困难.因此,对于需要大量逻辑判断的科学运算,GPU 高速计算的优势就会大打折扣.
起伏地表自由边界条件如下,其中Ω 代表自由表面:

|
(5) |
用有限差分法实现上述边界条件的问题在于处理边界网格点时需要对网格点特殊处理,例如,文献[29]中求解二维弹性波位移方程时通过对不同地形起伏情况下自由边界的具体分析,将整个二维空间离散点划分为24类,对每一类自由边界处的网格点选择了合理的表现方式,实现了起伏地表自由边界条件的数值化.然而,这种处理方式意味着大量的逻辑判断,这是GPU 所不擅长的,势必会大大降低程序的性能.本文采用类似于上一节单程波的边界处理方式,即每延拓一步使用公式(5)中在起伏地表以上为0,在起伏地表以下为1 的滤波函数filt(x,z)对波场滤波.不同之处在于单程波的滤波函数作用于频率域波场,而逆时偏移滤波函数作用于时间域波场.这种处理方式不但满足了起伏地表边界应力为0的边界条件,而且可以避免自由边界网格点细致的分类,从而可以避免大量的逻辑判断,试验表明,利用GPU 实现这种处理方式所需要的额外开销对程序性能的影响很小,可以忽略不计:
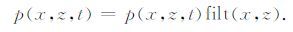
|
(6) |
起伏地表逆时偏移的主要计算部分包括沿时间正方向正传炮点波场(公式(4)),沿时间反方向反传接收点波场(公式(4)),起伏地表边界滤波(公式(6))以及成像条件.本文中选用互相关成像条件,原因是互相关成像条件容易实现,便于并行,不存在稳定性问题,并且可以处理多波至问题,不会丢失波场信息:
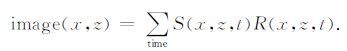
|
(7) |
公式(4),公式(6)和公式(7)表明,所有这些计算对每个空间网格点而言都是解耦的,因而可以并行实现,并且并行粒度非常小.与CPU 集群适合大粒度并行不同,GPU 计算核心多,对这种小粒度并行的问题更有优势.本文实验过程中选用的GPU型号是TeslaS1070,它由四块Tesla1060 显卡组成,每块显卡有240 个计算核心和4GB 的显存,选用的CUDA 版本是2.3.作为对比,CPU 的型号是Intel(R)XeonE5420 @ 2.50GHz, 配有24GBDDR2内存.
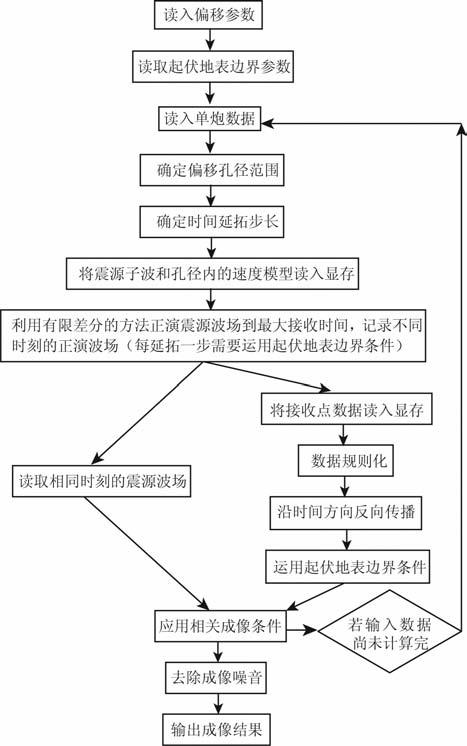
图 3是用利用GPU 实现起伏地表叠前逆时偏移流程图.与单程波偏移沿深度递推过程不同,逆时偏移沿着时间方向递推,因而可以直接将炮点或者检波点波场放置在真实网格点的位置,而不需要采用单程波偏移那样延拓一步判断然后加入新的波场的处理方式.需要强调的是,沿时间方向递推时,空间网格点依然是采用规则的网格,只需要在每延拓一步采用公式(6)的做法对波场做一次滤波即可.关于临时波场的存储以及低频成像噪音的去除方法与水平地表的逆时偏移方法一致,不再赘述.
|
图 3 用GPU 实现起伏地表逆时偏移流程图 Fig. 3 The flow chart of RTM using GPU for rugged topography |
本节中的实验数据采用的是国际上标准的SEG起伏地表模型(Amoco和BP公司设计的加拿大起伏地表逆掩断层模型)数据,其地质原型是加拿大英属哥伦比亚(British Columbia)东北部的逆掩断层构造.该数据共277炮,每炮480道接收,道间距15m, 中间激发,记录长度8s, 采样率4ms, 偏移距-3600~3600 m, 地形最大高差1527 m, 地层速度3600~6000 m/s.速度模型剖面长25km, 深10km.如图 4所示.从该图上可看到模型横向速度变化大,逆掩断层发育,且设计了几个负向构造,该模型的一些主要特征(如起伏地表形态、速度横向变化、逆掩断层和负向构造等)与我国南方山区复杂构造类似.分别使用单程波和逆时偏移对模型做了测试,结果如下:

|
图 4 SEG 起伏地表模型 Fig. 4 The SEG rugged topography model |
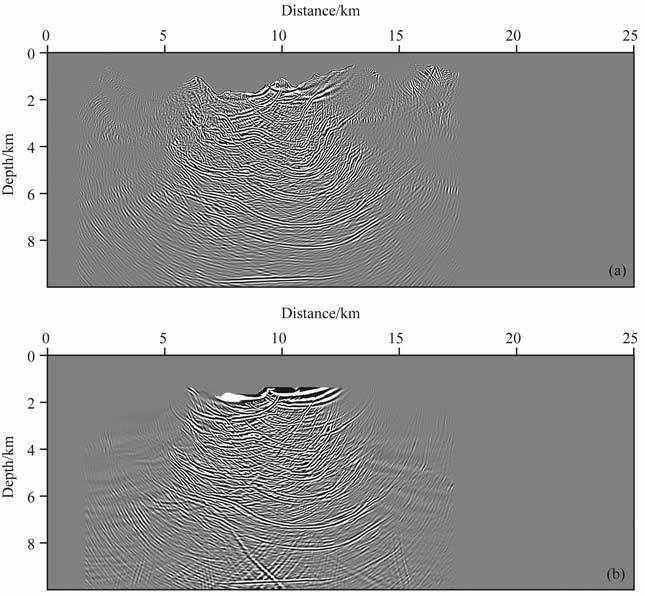
为了比较起伏地表单程波和逆时偏移结果的差异,首先对单炮数据做测试.选择模型炮点坐标为9450m 的单炮数据,偏移时两边各补300 个样点(4500m),对应偏移孔径为8100 m.偏移结果如图 5所示.图 5a是利用GPU 实现的逆时偏移的结果(去除低频成像噪音之后);图 5b是利用CPU 实现的单程波SP偏移结果.
|
图 5 单炮偏移结果 (a)逆时偏移结果;(b)单程波SP法偏移结果. Fig. 5 Migration result for one shot (a) The result of reverse time migration; (b) The result of the Split Step one-way wave method. |
(1) 从偏移结果对比,单程波对炮点高程以上的地层不能成像,这与前面的讨论是一致的.单程波偏移结果深部噪音比较严重,但是这些噪音在多炮偏移时可以相干抵消,对偏移结果影响不大.
(2) 从计算量上对比,逆时偏移沿时间方向递推步数为6605 步,单程波偏移需要偏移234 个频率,二者计算量相差大约10倍.
(3) 从计算时间上对比,基于GPU 实现的逆时偏移运算时间为15s, 而基于CPU 实现的SP 方法偏移时间为141s, 二者相差大约10倍.图 6是逆时偏移过程中炮点正传模拟的波场传播过程中6个不同时刻的波场快照,波场信息很丰富,并且可以清楚看到地震波沿近地表的传播过程.

|
图 6 逆时偏移过程中炮点正传波场不同时刻的快照 Fig. 6 The snapshots of 1^he shot wave-tield in reverse tme migration at six ditferent tme step |
图 7是277炮数据偏移的结果.首先比较偏移结果地表浅层部分,逆时偏移结果浅层地层清楚,断层连续性好.而单程波偏移结果较差,主要原因是上面分析的单程波偏移不能对炮点高程以上的地层进行成像,因而损失了部分有用信息.图 7c中的A 处与B处单程波偏移结果较差,同相轴已经完全断开,原因是这两处地层构造比较复杂,断层倾角很大,需要借助棱柱波,多次波等进行成像,而单程波对这些震相是无能为力的,逆时偏移没有角度限制,可以对这些震相精确成像,成像效果改善显著,如图 7b所示.对于图 7c中C 处的负向断层,两种偏移方法偏移结果均不理想,原因是观测系统的设计使得这部分地层的反射和透射等有用信息无法被接收到,因而也就无法成像.
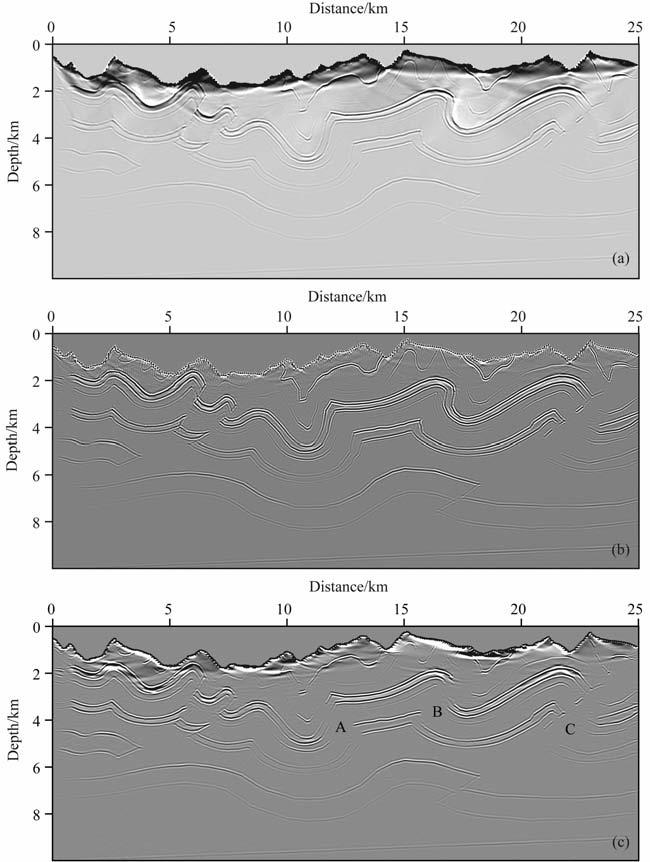
|
图 7 起伏地表偏移结果 (a)逆时偏移去噪之前的结果;(b)逆时偏移去噪之后的结果;(c)单程波SP法偏移结果. Fig. 7 Migration result for rugged topography (a) The result of reverse time migration before de-noise; (b) The result of reverse timemigration after de-noise; (c) The result of the Split Step method. |
本文详细介绍了起伏地表采集的地震数据处理的不同方案与策略.并着重介绍了起伏地表单程波偏移以及起伏地表逆时偏移的实现方法和流程.通过对理论模型的对比发现,单程波偏移无法对炮点高程以上的地层进行成像,因而对模型浅部进行成像时会损失有用信息,导致浅层成像效果较差,而逆时偏移不存在这个问题.
与单程波方法相比,逆时偏移沿时间方向递推,检波点的波场可以直接放置在相应的位置,而不需要像单程波方法那样在沿深度递推过程中延拓一步判断然后加入新的波场的处理方式.这对GPU 实现是有利的.另外,本文采用了类似于单程波滤波函数的方法在波场沿时间方向递推过程中对波场进行滤波,从而满足了起伏地表自由边界条件的要求.这种做法可以避免传统方法对边界网格点复杂的分类处理,避免大量的逻辑判断.从而为GPU 加速提供了基础,试验表明,利用GPU 实现这种处理方式所需要的额外开销对程序性能的影响很小,可以忽略不计.
本文中提出的方法已经在实际资料逆时偏移中使用,成像效果显著.
致谢对SEG 提供的起伏地表模型数据谨致谢意,感谢吉星吉达公司对本文的支持和帮助.
| [1] | Berryhill J R. Wave equation datuming. Geophysics , 1979, 44(8): 1329-1344. DOI:10.1190/1.1441010 |
| [2] | Berryhill J R. Wave equation datuming before stack (short note). Geophysics , 1984, 49(11): 2064-2067. DOI:10.1190/1.1441620 |
| [3] | Berryhill J A. Submarine canyons-Velocity replacement by wave equation datuming before stack. Geophysics , 1986, 51(8): 1572-1579. DOI:10.1190/1.1442207 |
| [4] | Yilmaz O, Lucas D. Prestack layer replacement. Geophysics , 1986, 51(7): 1355-1369. DOI:10.1190/1.1442186 |
| [5] | Faye J P, Jeannot J P. Wave-field datuming for land prestack migration. In: 57th Annual International Meeting, SEG, Expanded Abstracts. 1987, Session: S3.1 |
| [6] | Ellis N, Kitchenside P. Recursive implementation of redatuming, imaging, and layer replacement for irregular topography. In: 57th Annual International Meeting, SEG, Expanded Abstracts. 1989. 482~483 |
| [7] | Schneider W A Jr, Phillip L D, Paal E F. Wave-equation velocity replacement of the low-velocity layer for overthrust-belt data. Geophysics , 1995, 60(2): 573-579. DOI:10.1190/1.1443795 |
| [8] | Bevc D. Flooding the topography: Wave-equation datuming of land data with rugged acquisition topography. Geophysics , 1997, 62(5): 1558-1569. DOI:10.1190/1.1444258 |
| [9] | Yang K, Wang H Z, Ma Z T. Wave equation datuming from irregular surfaces using finite difference scheme. In: 69th Annual International Meeting, SEG, Expanded Abstracts. 1999. 1456~1468 |
| [10] | 杨锴, 王华忠, 程玖兵, 等. 非水平观测面有限差分法叠前波动方程基准面校正. 石油地球物理勘探 , 2002, 37(2): 62–70. Yang K, Wang H Z, Cheng J B, et al. Prestack wave equation datum correction from non-flat surface with finite-difference scheme. Oil Geophysical Prospecting (in Chinese) , 2002, 37(2): 62-70. |
| [11] | Wiggins J W. Kirchhoff integral extrapolation and migration of nonplanar data. Geophysics , 1984, 49(8): 1239-1248. DOI:10.1190/1.1441752 |
| [12] | Reshef M. Depth migration from irregular surfaces with depth extrapolation methods (short note). Geophysics , 1991, 56(1): 119-122. DOI:10.1190/1.1442947 |
| [13] | Beasley C, Lynn W. The zero-velocity layer: Migration from irregular surfaces. Geophysics , 1992, 57(11): 1435-1443. DOI:10.1190/1.1443211 |
| [14] | 何英, 王华忠, 马在田, 等. 复杂地形条件下波动方程叠前深度成像. 勘探地球物理进展 , 2002, 25(3): 13–19. He Y, Wang H Z, Ma Z T, et al. Pre-stack wave equation depth migration for irregular topography. Progress in Exploration Geophysics (in Chinese) , 2002, 25(3): 13-19. |
| [15] | Geiger H D, Bancroft J C. Equivalent offset prestack migration for rugged topography. In: Expanded Abstracts of 66th Annual International SEG Meeting. 1996. 447~450 |
| [16] | Zhu X H, Angstman B G, Sixta D P. Overthrust imaging with tomo-datuming: A case study. Geophysics , 1998, 63(1): 25-38. DOI:10.1190/1.1444319 |
| [17] | Margrave G F, Yao Z S. Downward extrapolation from topography with a laterally variable depth step. In: Expanded Abstracts of 70th Annual International SEG Meeting. 2000. 481~484 |
| [18] | Mi Y P, Margrave G F. Prestack depth imaging from topography with a Fourier method. In: Expanded Abstracts of 71st Annual International SEG Meeting. 2001. 1045~1048 |
| [19] | Shragge J C, Sava P. Wave-equation migration from topography. In: 75th Annual International Meeting. SEG, Expanded Abstracts. 2005. 1842~1845 |
| [20] | Al-Saleh S M, Margrave G F, Bancroft J C. Explicit wavefield extrapolation directly from topography. SEG Expanded Abstracts , 2006, 25: 2534. |
| [21] | Xiong X J, He Z H, Huang D J. One-way wave equation seismic prestack forward modeling with irregular surfaces. Applied Geophysics , 2006, 3(1): 13-17. DOI:10.1007/s11770-006-0002-7 |
| [22] | 王成祥, 赵波, 张关泉. 基于起伏地表的混合法叠前深度偏移. 石油地球物理勘探 , 2002, 37(3): 219–223. Wang C X, Zhao B, Zhang G Q. Rugged surface oriented hybrid pre-stack depth migration. Oil Geophysical Prospecting (in Chinese) , 2002, 37(3): 219-223. |
| [23] | 程玖兵, 马在田, 陶正喜, 等. 山前带复杂构造成像方法研究. 石油地球物理勘探 , 2006, 41(5): 525–529. Cheng J B, Ma Z T, Tao Z X, et al. Imaging study of piedmont complex structures. Oil Geophysical Prospecting (in Chinese) , 2006, 41(5): 525-529. |
| [24] | 田文辉, 李振春, 张辉, 等. 起伏地表条件下的波场上延法叠前深度偏移. 中国石油大学学报(自然科学版) , 2006, 30(5): 19–22. Tian W H, Li Z C, Zhang H, et al. Wave-field upward continuation pre-stack depth migration based on irregular topography. Journal of China University of Petroleum (Edition of Natural Science) (in Chinese) , 2006, 30(5): 19-22. |
| [25] | 陈爱萍, 邹文, 李亚林, 等. 起伏地表波动方程叠前深度偏移技术——以川东复杂地区应用为例. 石油物探 , 2008, 47(5): 470–476. Chen A P, Zou W, Li Y L, et al. Wave equation pre-stack depth migration technology in rolling surface area:application case in complex area of east Sichuan. Geophysical Prospecting for Petroleum (in Chinese) , 2008, 47(5): 470-476. |
| [26] | 杨海生. 基于起伏地表的合成炮叠前深度偏移. 石油地球物理勘探 , 2007, 42(4): 380–386. Yang H S. Relief surface-based prestack depth migration of synthetic shot records. Oil Geophysical Prospecting (in Chinese) , 2007, 42(4): 380-386. |
| [27] | Rajasekaran S, McMechan G A. Prestack processing of land data with complex topography. Geophysics , 1995, 60(6): 1875-1886. DOI:10.1190/1.1443919 |
| [28] | 徐义. 格子法在起伏地表叠前逆时深度偏移中的应用. 地球物理学进展 , 2008, 23(3): 839–845. Xu Y. Prestack reverse-time migration by the grid method. Progress in Geophysics (in Chinese) , 2008, 23(3): 839-845. |
| [29] | 董良国, 郭晓玲, 吴晓丰, 等. 起伏地表弹性波传播有限差分法数值模拟. 天然气工业 , 2007, 27(10): 38–41. Dong L G, Guo X L, Wu X F, et al. Finite difference numerical simulation for the elastic wave propagation in rugged topography. Natural Gas Industry (in Chinese) , 2007, 27(10): 38-41. |
| [30] | 李博, 刘国峰, 刘洪. 地震叠前时间偏移的一种图形处理器提速实现方法. 地球物理学报 , 2009, 52(1): 245–252. Li B, Liu G F, Liu H. Amethod of using GPU to accelerate seismic pre-stack time migration. Chinese J. Geophys. (in Chinese) , 2009, 52(1): 245-252. |
| [31] | 刘国峰, 刘洪, 李博, 等. 山地地震资料叠前时间偏移方法及其GPU实现. 地球物理学报 , 2009, 52(12): 3101–3108. Liu G F, Liu H, Li B, et al. Method of prestack time migration of seismic data of mountainous regions and its GPU implementation. Chinese J. Geophys. (in Chinese) , 2009, 52(12): 3101-3108. |
| [32] | Micikevicius P. 3D finite difference computation on GPUs using CUDA. In: Proceedings of 2nd Workshop on General Purpose Processing on Graphics Processing Units. Washington DC, 2009. 79~84 |
| [33] | 刘红伟, 李博, 刘洪, 等. 地震叠前逆时偏移高阶有限差分算法及GPU实现. 地球物理学报 , 2010, 53(7): 1725–1733. Liu H W, Li B, Liu H, et al. The algorithm of high order finite difference pre-stack reverse time migration and GPU implementation. Chinese J. Geophys. (in Chinese) , 2010, 53(7): 1725-1733. |
| [34] | 刘红伟, 邹振, 刘洪, 等. 地震叠前逆时偏移中的去噪与存储. 地球物理学报 , 2010, 53(9): 2171–2180. Liu H W, Zou Z, Liu H, et al. The problems of denoise and storage in seismic reverse time migration. Chinese J. Geophys. (in Chinese) , 2010, 53(9): 2171-2180. |
| [35] | Foltinek D, Eaton D, Mahovsky J, et al. Industrial-scale reverse time migration on GPU hardware. In: 79th Annual International Meeting. SEG Expanded Abstracts. 2009, 28: 2789~2793 |
| [36] | Stoffa P L, Fokkema J T, de Luna Freire R M, et al. Split-step Fourier migration. Geophysics , 1990, 55(4): 410-421. DOI:10.1190/1.1442850 |
| [37] | Gray S H, Marfurt K J. Migration from topography: improving the near-surface image. Canadian Journal of Exploration Geophysics , 1995, 31(1-2): 18-24. |
 2011, Vol. 54
2011, Vol. 54


