2. 中国石油塔里木油田勘探开发研究院,新疆库尔勒 841000
2. Research Institute of Exploration and Development, Petrochina Tarim Oilfield Company, Kuerle 841000, China
1968年Claerbout[1]提出,在一维介质的情况下,地下震源放炮,地表检波器接收的地震记录自相关的单边等于地表检波器的自激自收反射地震记录.Katz[2]把此原理应用到实际的逆VSP 中获得了专利.Rickett等[3]推测3-D 介质的反射响应可以通过地震噪声的自相关来得到,称之为日光成像.Schuster[4, 5]提出了地震相干的概念,将日光成像延拓到任意分布的震源以及反射层中去.地震相干是通过对存在的地震道做互相关、褶积或者反褶积产生新地震记录的一种处理方法[6].
地震相干在实际中的应用,得益于Bakulin等[7]提出的虚源理论.在假设复杂地表下面的介质要相对简单的前提下,他们利用VSP观测系统的特殊性,对地震道相关并叠加后,产生检波器放炮、检波器接收的虚源,以解决复杂地表对成像影响的问题.具体应用范围包括断裂带识别[8]、盐洞建模以及4-D VSP[9]等等.此外,Halliday[10]通过利用地震相干把面波分离出来,从而能比较好的去除面波.
地震相干在理论上的进展主要是格林函数代表理论.Wapenaar等[11, 12]对不存在内在衰减的介质提出了格林函数代表理论,随后Snieder[13]以及Wapenaar等[14]则把代表理论扩展到了存在内在衰减的介质中.
对于不存在内在衰减的介质,在远场近似的情况下,检波器处的虚拟震源产生的地震记录可以用真实震源地震记录的相关来表示:

|
(1) |
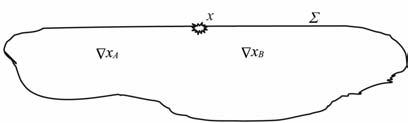
其中xA,xB是两个检波器所处位置,G(xA,x,t)和G(xB,x,t)是点源x激发,检波器xA,xB接收到的两条地震脉冲记录.格林函数G(xA,x,-t)是G(xA,x,t)的时间逆转的形式.ρ 以及c分别是在闭合面Σ 上的密度以及速度常数,* 代表褶积,公式右边是要对完全包围检波点xA,xB的Σ 面上做积分(图 1),得到的结果是公式左边G(xA,xB,t)与它的时间逆转G(xA,xB,-t)的叠加.在G(xA,xB,t)满足因果律的情况下,G(xA,xB,t)即为公式右边的结果取t>0一边的数据.即在xB处产生震源,xA处接收的格林函数可以通过xA,xB处记录的格林函数表示.
|
图 1 积分面Σ 为包围检波器xA,xB的闭合面 Fig. 1 The integration surface Σ is a closed surface surround the receivers xA,xB |
地震相干的格林函数代表理论所要求的数据都是对地层的点源脉冲响应,实际上能记录到的是地震波形数据,并不是理论上的格林函数.所以在很多情况下地震相干是直接用地震道代替格林函数来做相关的,这样必然会导致分辨率的下降.于是Vasconcelos[15]提出通过反褶积来做地震相干:
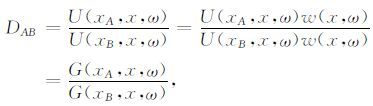
|
(2) |
其中U(xA,x,ω)是在x点作为震源,检波器xA接收的地震记录在频率域的表示,G(xA,x,ω)与w(x,ω)则分别为相应的格林函数以及震源子波在频率域的表示.对DAB积分可以得到虚源记录,具体的实施可以参看原文.这样做的好处是可以消除震源子波的影响,提高分辨率.不过其前提假设是一个地层的脉冲响应G等于直达波G0 和散射波GS的叠加,并且G0 要远大于GS.在实际中Bakulin[9]对虚源法的改进也是用类似的方法.此方法的缺点是G0要远大于GS,否则丢失的高阶项将会产生比较大的误差.
国内对地震相干的研究有常旭等[16]对地震相干偏移以及数据自参照偏移的关系讨论,文中对模拟数据使用不同偏移方法的结果进行了对比.
本文在地震相干过程中,利用地震相干的特殊性,提取出震源子波,通过特殊的子波反褶积方法,尽可能的去除地震子波对地震相干的影响,从而比较简便有效的实现地震相干成像.
2 地震相干 2.1 相干方法假设U(xA,x,t)是震源在x,检波器在xA的一道地震记录,那么它可以表示为
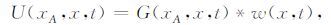
|
(3) |
其中G(xA,x,t)为相应的脉冲响应,w(x,t)为震源子波.从而可以得到以下方程:
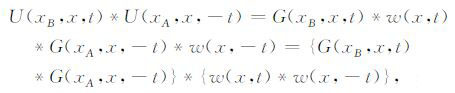
|
(4) |
定义新的子波p(x,t)= {w(x,t)*w(x,-t)},是一个零相位子波.那么有地震道的自相关等于脉冲响应的自相关与子波自相关的褶积.
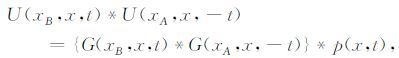
|
(5) |
设计一个滤波算子F(x,t),整形新的子波p(x,t)成脉冲δ(t).这样可以比较简便的利用地震道数据做相干成像.
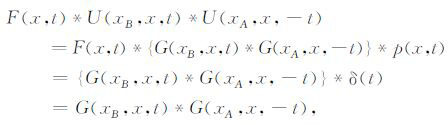
|
(6) |
所以,对于公式(1),在实际应用中做如下变换:
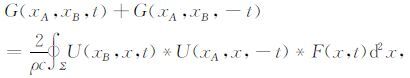
|
(7) |
其中F(x,t)是一个整形新的子波p(x,t)成脉冲δ(t)的算子.
2.2 子波提取在假设反射系数是白噪声的情况下,震源子波自相关可以用地震道自相关替代.理论上因为在反射系数是白噪声的情况下,它的自相关类似于脉冲,而子波自相关与脉冲的褶积,就是子波自相关自身.不过由于地震子波的长度是有限的,实际应用中是取地震道自相关靠近零点附近的一部分来近似子波自相关.
对于地震相干,在前面假设成立的情况下:
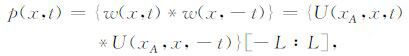
|
(8) |
其中{U(xA,x,t)*U(xA,x,-t)}[-L∶L]表示取地震道自相关靠近零点的一段,长度为2L+1.但是,在实际应用中参数L的选取比较难以把握,所以在实施时,选取不同检波器xi记录到震源x生成数据的多个自相关的一段[-L∶L],叠加来代替这一炮的震源子波自相关.这样能比较准确地估计出震源子波的自相关.即:
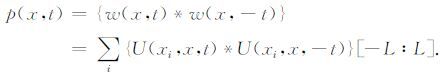
|
(9) |
求出地震子波p(x,t)后,如上节所述,一般情况下是直接利用维纳滤波设计滤波算子F(x,t)进行子波整形.即:
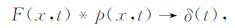
|
(10) |
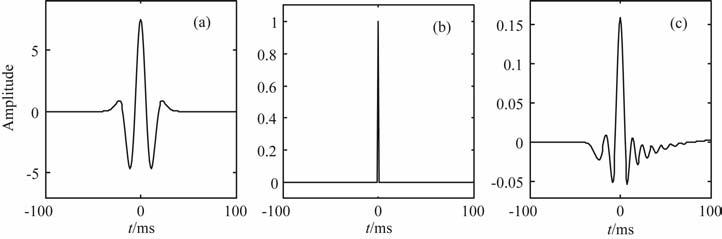
但实际整形过程中发现,对于零相位子波p(x,t),要进一步整形成脉冲是比较困难的.如图 2所示,对于一个输入信号(图 2a),设计一个期望输出(图 2b),利用最小平方滤波方法可以得到一个滤波算子F(x,t),把滤波算子和输入信号褶积,得到实际输出(图 2c).从结果上可以看到,虽然结果要比输入信号有所改善,但是和期望输出还相差很多.原因可能是因为输入的信号是一个子波的自相关,是零相位双边的,整形结果必然不是很理想.需要用其他的方法实施整形.
|
图 2 传统整形过程 Fig. 2 The conventional procedure of wavelet shaping |
p(x,t)是一个零相位子波,所以可以假设存在一个最小相位子波h(x,t),使得它的自相关等于p(x,t).最小相位子波h(x,t)的求取方法是先求出p(x,t)的振幅谱,h(x,t)的振幅谱正好是p(x,t)振幅谱的开方.求出h(x,t)的振幅谱后,可以利用Wold-Kolmogorov 公式求取一个最小相位,这样h(x,t)就能确定了.
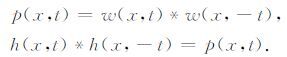
|
(11) |
这样可以设计一个滤波算子i(x,t),整形最小相位子波h(x,t)成零延迟单边脉冲.
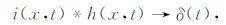
|
(12) |
滤波算子i(x,t)的自相关是一个双边算子,可以把最小相位子波h(x,t)的自相关整形成脉冲.

|
(13) |
可知,滤波算子i(x,t)的自相关即为所需要的滤波算子F(x,t).
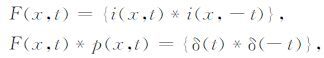
|
(14) |
图 3给出了地震子波整形过程,从求取过程可见,F(x,t)并不是使p(x,t)与脉冲在最小平方意义上最小的滤波算子.然而,从实际结果来看,这要好于最小平方滤波,尤其是在原始子波接近最小相位的情况下,子波的旁瓣压缩的比较明显.这主要是基于两点:首先最小相位子波可以比较好的整形成零延迟脉冲;其次通过这种方法整形结果的自相关和双边的零延迟脉冲是非常相近的.

|
图 3 整形过程(a)原始的震源子波;(b)此子波的自相关;(c)利用公式(11)从(b)求出的最小相位子波,它的自相关(d)与(b)对比发现非常接近;(e)利用(12)式对(c)的整形结果;(f)利用(14)式对(b)的整形结果. Fig. 3 The shaping procedure described in the article |
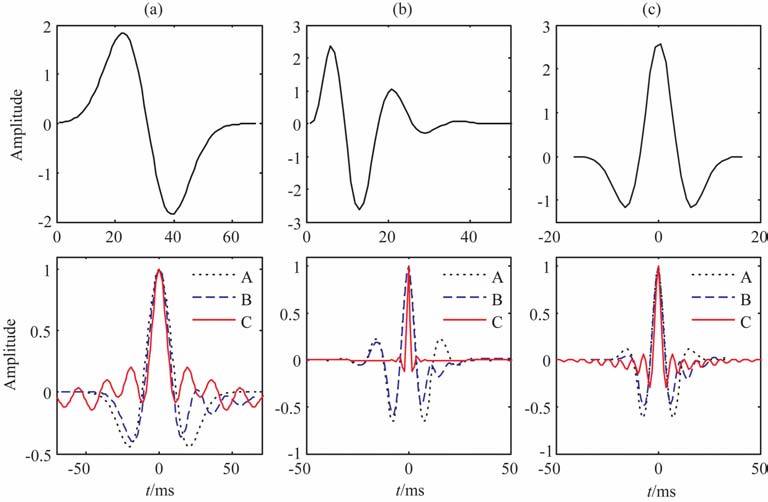
对于原始子波比较偏离最小相位的子波,这种方法整形结果稍微有些震荡,但就主瓣振幅与旁瓣振幅相比而言,要要好于最小平方滤波.图 4中为使用三种不同相位子波的自相关做最小平方滤波以及前面提出方法整形结果的对比.对于三个不同子波,本文使用的方法都要比直接整形结果要好一些,尤其是在图 4b中原始子波比较接近最小相位的时候,整形结果比较明显.
|
图 4 三个不同相位子波(a, b, c)自相关整形结果对比A,B,C依次为原始子波自相关,传统整形结果以及本文使用方法整形结果. Fig. 4 Compare the results of shaping the autocorrelation of three different phase wavelets b and c.A,B,C are in turn the autocorrelation of the wavelet, the shaping result of the conventional method and the method described in the article. |
滤波算子F(x,t)求出以后,便可开始生成虚源数据.由于公式(7)是积分形式的,在实际应用中这种观测系统是不可能达到的,需要把它离散化,用求和代替积分.对于任意检波器xA,xB,如果接收到N炮数据x1,x2,… xN有:

|
(15) |
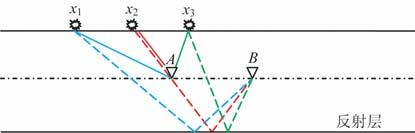
可以看到这里有对多个震源记录相关叠加的过程,但是并不是所有的源都起着同等的作用.只有那些处在固定相位点[17](如图 5所示,炮点x2 对于反射层以及检波器A,B处于固定相位点,而炮点x1,x3不处于)附近的源的作用最大,即叠加后处于其他相位点的源的效果将会抵消掉,这也是能够生成A点产生虚震源,B点接收的记录的基础.在地下介质构造未知的情况下,哪些源是处在固定相位点附近也是无法确定的,这就要求在生成虚源记录的时候尽可能选择大的孔径,使用尽可能多的震源,以保证对于不同的反射层都有对应的震源处在固定相位点附近.同时,炮点之间的距离[18]对结果的影响也是非常大的,如果炮点之间的距离太大,将会导致假频现象,结果将会非常差.Bakulin 等[9]认为复杂地表有利于虚源数据的生成.这是因为复杂地表的散射相当于额外的震源,缩小了震源之间的距离.
|
图 5 对应虚源A及检波点B不同相位点的炮点 Fig. 5 Shot position at different phase for the virtual source A and receiver B |
公式(15)中要求求和是在闭合曲面上进行的,这相当于要求震源分布包围检波器,这在现有的观测系统中是不可能达到的.VSP一般是地表震源放炮,地下检波器接收.在这种情况下,由于检波器以下震源的缺失,检波器虚源只能产生向下的能量,没有向上的能量.这对于消除检波器上面复杂介质的影响有积极的作用.
地震相干一般的实施流程如图 6所示.
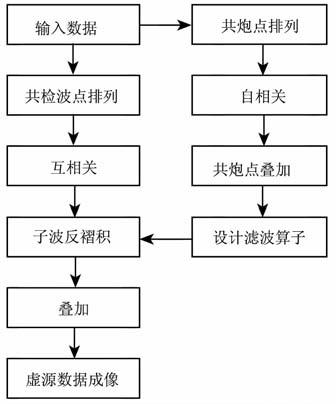
|
图 6 生成虚源数据流程图 Fig. 6 The procedure to generate virtual source data |
(1) 设计滤波算子.按照公式(9),按共炮点排列数据,得到共炮点道集.对每一道记录做自相关,得到自相关共炮点道集.对道集进行共炮点叠加,并取最终结果靠近0 点附近的一段[L∶ -L]作为每一炮的震源子波自相关.利用震源子波自相关,根据前面的方法设计出每一炮的滤波算子.
(2) 地震相干反褶积.按共检波点排列数据.选取一个检波点作为虚源,其他检波器(包括虚源本身)作为虚检波器接收数据.将选定检波器的道集与其他的共检波点道集相同炮号的道做互相关.用前面得到滤波算子,与相关道集对应炮做褶积.这样就得到了虚源检波器与其他检波器之间的互相关反褶积道集.
(3) 叠加.对前面的互相关反褶积道集进行叠加,并且取时间t>0 的一段,这就产生了一道虚源放炮,其他检波器接收的共炮点记录.
(4) 重复步骤2,3可以得到所有的虚源记录.
(5) 成像.对得到的虚源数据进行分析成像.
4 二维模型模拟图 7是一个海上模型.海底地表起伏并且速度非常混乱,可以看到几个比较明显的低速层,而比较深的地下要简单的多.这与实际地质结构也比较接近,并且复杂的地表结构经常给常规的地震勘探造成比较大的困难,而如前面所述,复杂地表在某种程度上是有利于地震相干的.模型在1800~1850 m处有一个50 m 比较薄的低速层.通过地震相干处理,可以比较清晰地识别出这个薄层.在2500~3100m 之间有一个比较明显的阶梯斜面.在3900m以及4600m 处各有一个水平的反射层.
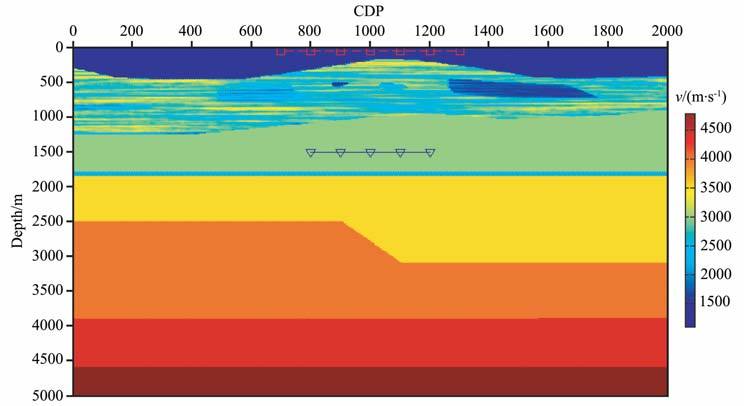
|
图 7 上覆地层复杂,地下相对简单的二维速度模型 Fig. 7 The 2-D velocity model with complex overburden and simple underground structure |
对模型应用有限差分实现正演,在海面以下50m处CDP700~1300 之间每隔3 个CDP 有一个震源,总共有200个震源.在海面以下1500m 处,CDP800~1200之间每隔4个CDP 有一个检波器,总共有100个检波器.每两个CDP之间的间隔都是8m.
查看模型在CDP1000处检波器(第50个检波器)记录到的共检波点记录(图 8),可见在复杂上覆地层情况下的记录同相轴明显变形.如果直接利用此数据进行成像分析,在静校正以及速度分析方面要花费很多时间以及精力.通过地震相干,可以得到地下任意一个检波点处作为虚源,任意一个检波点接收的记录,从而避开复杂上覆地层.
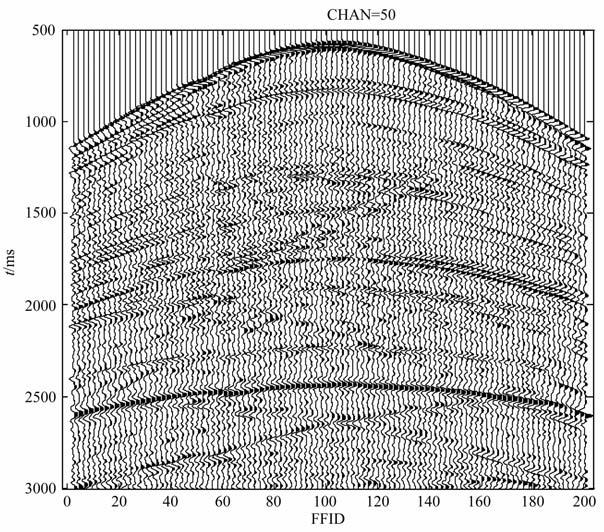
|
图 8 原始记录第50个共检波点道集 Fig. 8 The 50th common receiver record gather |
按照图 6的流程,本方法将对相关后的结果作子波反褶积,压制子波旁瓣,以提高分辨率.图 9 是第50个共检波点道集地震道自相关结果反褶积前后的对比,由于是自相关,取的数据是时间-100~2500之间的一段.观察可见反褶积后结果旁瓣较好的压制,使得道集分辨率有比较好的提高,这有益于叠加后的结果.对此道集进行叠加,将得到一道记录,即第50个检波器的自激自收记录.将第50个共检波点道集与其他所有共检波点道集对应炮记录做互相关,反褶积并叠加,可以得到第50 个检波器产生的虚源共炮点道集(如图 10所示).
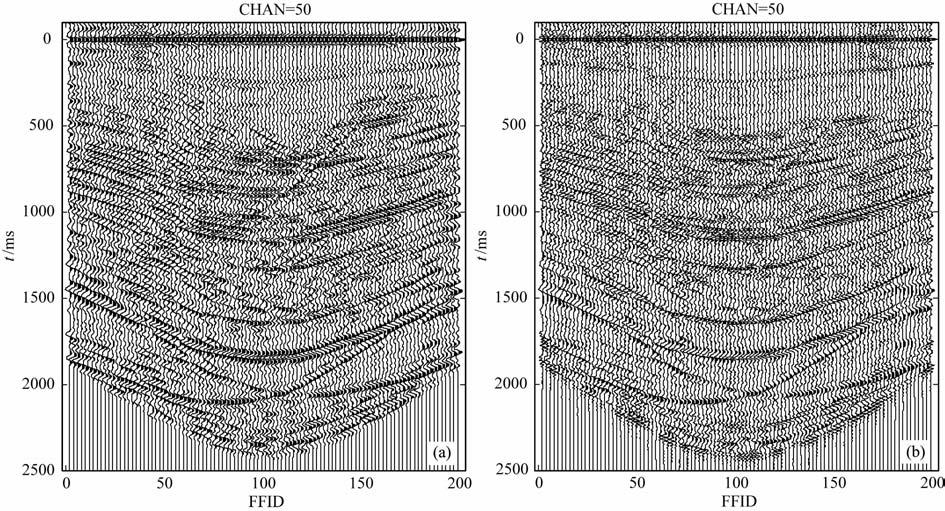
|
图 9 第50个共检波点道集的自相关(a)与自相关反褶积后结果(b) Fig. 9 The autocorrelation of the 50th common receiver gather (a) andthe deconvolution result of the autocorrelation (b) |
|
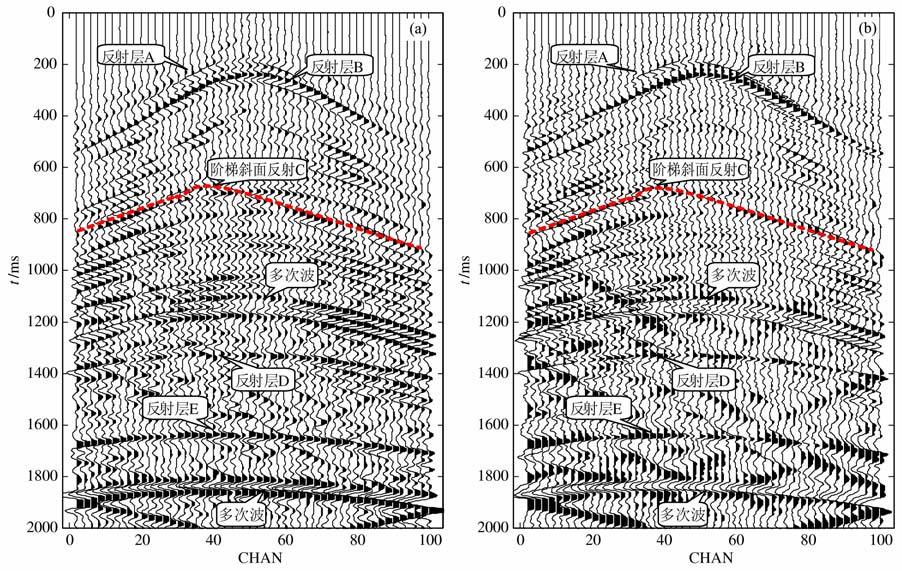
图 10 直接用地震道(a)以及用反褶积后结果(b)生成的第50个检波点的虚源共炮点道集 Fig. 10 The virtual source common shot gather of the 50th receiver generated from the seismic data without deconvolution (a) and with deconvolution (b) |
对比直接用地震道(图 10a)以及反褶积后结果(图 10b)生成的虚源共炮点道集结果可以发现,两者都能比较好地显示出地下水平反射层产生的反射同相轴,最大的区别是反褶积后结果同相轴要紧凑一些.反褶积后结果由于子波旁瓣压缩,主瓣要明显一些,能够更加清晰地识别出同相轴.在道集上也都能够显示出2500~3100 m 之间的阶梯斜面;直接用地震道生成的数据由于子波主瓣不够明显,相对难以准确地识别,而加入反褶积后结果明显.然而,同样可以看到,在1200ms以及1800ms附近有几个同相轴是多次波,由于它们和初次反射波难以分辨,所以很容易造成假象,这将是地震相干成像面临的比较重要的问题.在两个道集上都有线性噪声,产生的原因有可能是正演程序对吸收边界做的不好,以至于从模型边界都产生了不该有的反射.
如前所述方法,可以生成100炮100个检波器接收的虚源共炮点道集.在地下结构比较简单的情况下,对生成的虚源数据做速度分析将要简单得多.速度分析后使用Kirchhoff叠前深度偏移对数据进行成像,得到结果如图 11b所示.
|
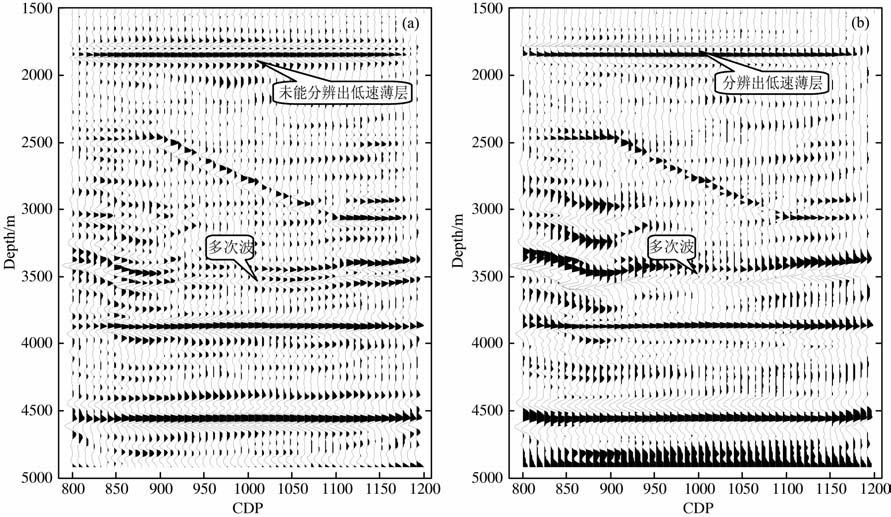
图 11 利用反褶积前(a)后(b)虚源数据进行叠前深度偏移结果对比 Fig. 11 Compare of the PSD migration result of the virtual source data before (a) and after deconvolution (b) |
由于虚源数据的震源以及检波器都处在表面以下1500m, 偏移结果深度是基于表面以下1500 m的.对比直接用地震道图 11a以及反褶积后图 11b生成虚源数据成像结果.最大的差别是反褶积后结果同相轴压缩,分辨率有所提升.最明显的标志是1800~1850m 之间的一个50m 的薄层在反褶积后结果能够非常清晰地分辨,而直接使用地震道的结果两个反射层交织在了一起.在3500 m 处的一个多次波在两个结果里都有显示,其他的反射层也都有较好的成像.
5 结论本文研究了基于地震相干避开复杂上覆地层对地震波的影响,利用VSP 数据估计地震虚源,生成了检波器放炮,检波器接收的虚源数据,直接对目的地层进行成像的方法.实验结果表明,即使在地表以及上覆地层非常复杂的情况下,只要足够多检波器能够处于复杂地表以下构造相对简单的位置,直接用地震道生成的虚源数据是有可能比较好的对目的层成像的.而在生成虚源数据过程中加入反褶积算子能够压制子波旁瓣,使得两个非常靠近的反射同相轴主瓣更少地受到其他旁瓣的影响,从而在一定程度上提高成像分辨率.
| [1] | Claerbout J F. Synthesis of a layered medium from its acoustic transmission response. Geophysics , 1968, 33(2): 264-269. DOI:10.1190/1.1439927 |
| [2] | Katz L J. Inverse vertical seismic profiling while drilling: United States Patent, Patent Number: 5,012,453, 1991 http://cn.bing.com/academic/profile?id=19297334&encoded=0&v=paper_preview&mkt=zh-cn |
| [3] | Rickett J, Claerbout J. Passive seismic imaging applied to synthetic data. Stanford Exploration Project. 1996. 87~94 |
| [4] | Schuster G T. Theory of Daylight/Interferometric Imaging: Tutorial. 63rd annual EAGE meeting, Expanded Abstracts. Salt Lake City: University of Utah, 2001, A-32 |
| [5] | Schuster G T, Yu J, Sheng J, et al. Interferometric/daylight seismic imaging. Geophys. J. Int , 2004, 157(2): 838-852. |
| [6] | Draganov D, Ghose R, Ruigrok E, et al. Seismic interferometry, intrinsic losses and Q-estimation. Geophysical Prospecting , 2010, 58(3): 361-373. DOI:10.1111/(ISSN)1365-2478 |
| [7] | Bakulin A, Calvert R. Virtual source: New method for imaging and 4D below complex overburden. 74th Annual Meeting, SEG Expanded Abstracts. 2004. 2477~2480 |
| [8] | Chavarria J A, Goertz A, Karrenbach M, et al. The use of VSP techniques for fault zone characterization: An example from the San Andreas Fault. The Leading Edge , 2007, 26(6): 770-776. DOI:10.1190/1.2748495 |
| [9] | Bakulin A, Calvert R. The virtual source method: Theory and case study. Geophysics , 2006, 71(4): SI139-SI150. DOI:10.1190/1.2216190 |
| [10] | Halliday D F, Curtis A, Robertsson J O A, et al. Interferometric surface-wave isolation and removal. Geophysics , 2007, 72(5): A69-A73. DOI:10.1190/1.2761967 |
| [11] | Wapenaar K. Retrieving the elastodynamic Green's function of an arbitrary inhomogeneous medium by cross correlation. Physical Review Letters , 2004, 93(25): 254301. DOI:10.1103/PhysRevLett.93.254301 |
| [12] | Wapenaar K, Fokkema J. Green's function representations for seismic interferometry. Geophysics , 2006, 71(4): SI33-SI46. DOI:10.1190/1.2213955 |
| [13] | Snieder R. Extracting the Green's function of attenuating heterogeneous media from uncorrelated waves. J. Acoust. Soc. Am , 2007, 121(5): 2637-2643. |
| [14] | Wapenaar K, Slob E, Snieder R. Seismic and electromagnetic controlled-source interferometry in dissipative media. Geophysical Prospecting , 2008, 56(3): 419-434. DOI:10.1111/j.1365-2478.2007.00686.x |
| [15] | Vasconcelos I, Snieder R. Interferometry by deconvolution: Part2—Theory for elastic waves and application to drill-bit seismic imaging. Geophysics , 2008, 73(3): S129-S141. DOI:10.1190/1.2904985 |
| [16] | 常旭, 刘伊克, 王辉, 等. 地震相干偏移与数据自参照偏移的关系. 地球物理学报 , 2009, 52(11): 2840–2845. Chang X, Liu Y K, Wang H, et al. Seismic interferometric migration and data-referenced-only migration. Chinese J. Geophys. (in Chinese) , 2009, 52(11): 2840-2845. |
| [17] | Schuster G T. Seismic Interferometry. Cambridge: Cambridge University Press, 2009 : 30 -60. |
| [18] | Mehta K, Snieder R, Calvert R, et al. Acquisition geometry requirements for generating virtual-source data. The Leading Edge , 2008, 27(5): 620-629. DOI:10.1190/1.2919580 |
 2011, Vol. 54
2011, Vol. 54


