2. 武汉大学地球空间环境和大地测量重点实验室, 武汉 430079
2. Key Lab. of Geospace Environment and Geodesy, Wuhan University, Wuhan 430079, China
声学研究中发现两台仪器记录到的背景噪声互相关叠加包含了介质的本征信息.Weaver & Lobkis[1~3]给出了互相关叠加的数学模型.这一发现很快被应用于地震背景噪声观测中.观测资料的处理结果证实了两台站长时间记录到的数据互相关函数的叠加包含有面波的频散信息[4~7].在一定的条件下地震尾波的互相关叠加也含有同样的信息[8~10].Sabra等[7]以及Shapiro等.[8]将这一方法运用于美国南加州地震台网,成功地提取出7.5~15s的高频面波群速度信息.Yang 等[11]尝试把这一方法用于整个欧洲大陆,用时间长度为一年的地震背景噪声资料互相关叠加,提取出10~50s周期的Rayleigh波群速度频散.这些成功的例子说明,地震背景噪声中确实包含了地球介质的本征信息.Yao 等(2006)[12]尝试着从背景噪声中提取相速度频散信息,其基本假设是互相关函数负导数的相位与介质的格林函数的相位相同.Snieder(2004)[13]假设噪声源均匀分布,利用稳相法近似证明了两台背景噪声互相关函数的负导数的相位确实与两台间介质的格林函数的相位相同.事实上,截至目前为止所有利用地震背景噪声或尾波提取面波频散信息的研究都隐含一个基本假设,那就是两台站地震背景噪声或尾波的互相关函数叠加的负导数(称之为经验格林函数)等价于两台站之间介质的格林函数,本文称之为等价格林函数假设.实际测量表明,对于群速度信息,基于什么假设都不会影响其测量结果.但对于相速度的测量却不同,因为相速度测量需要知道具体的理论相位表达形式,不同的假设将导致不同的测量结果.
目前所作的群速度测量结果在可比较的频率范围内与传统的依赖地震的方法测量的结果基本是一致的.这似乎说明等价格林函数假设是成立的.但必须注意几个事实:(1)互相关函数的叠加结果不满足格林函数的时空互易性[8, 12],说明噪声源并非均匀分布.(2)基于格林函数假设测得的相速度与传统的双台法测得的相速度有系统的偏差,而且这种偏差随周期的增大而增大[12].(3)已有的研究没有涉及群速度和相速度测量的理论误差.
本文将从弹性动力学面波激发公式出发,探讨地震背景噪声互相关函数叠加的面波理论表达形式,为相速度和群速度测量提供理论依据.
2 NCF的面波理论表达形式在区域面波的研究中,地球作平面近似,或作展平近似.为理论上探讨方便,设地球为横向均匀的水平层状模型.
设观测点x的背景场为Φ(x,t),y的背景场为Φ(y,t),两背景场的互相关函数定义为

|
(1) |
设地震背景噪声是随机震源产生的波叠加而成.观测点为x,震源为xs 激发的面波垂直分量频率域可表示为[14]
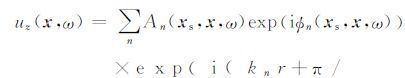
|
(2) |
其中An(xs, x,ω)为n阶振型的振幅谱,Φn(xs, x,ω)是与震源及方位角有关的相位,r为震源到接收点的水平距离,对所有振型求和.
台站x1 的背景噪声记录可以看成该区域内所有噪声源激发波的叠加.由于已经假设介质是横向均匀的,这种叠加可简单的表示为
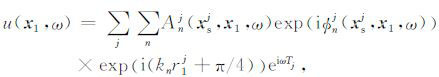
|
(3) |
角标j对所有噪声源求和,Tj为第j个震源发震时刻与参考时间的时差.
对台站x2 的噪声记录可以像(3)式那样做同样的处理.两台站的噪声记录作互相关,在频率域内得
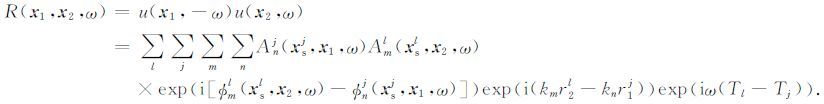
|
(4) |
设统计意义上不同震源的记录相互独立,不同模式之间相互独立.则(4)式中必须m=n,l=j.(4)式的统计平均为
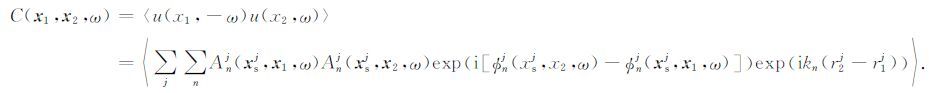
|
(5) |
按照r2j-r1j >0(定义为右行波,位相从台站1传到台站2,参考图 1)和r2j-r1j <0(定义为左行波,位相从台站2传到台站1)把(5)式分成两部分,则
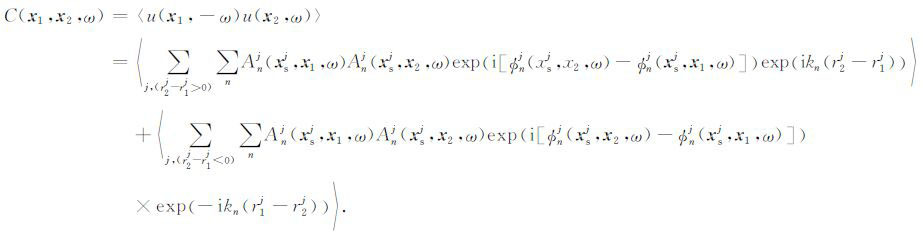
|
(6) |

|
图 1 五角星代表震源,实三角形表示台站,空心三角形表示两台站之间的距离.灰度区为有效震源区 Fig. 1 Pentacles represent sources, solid triangles represent stations and gray areas indicate e |
令右行波
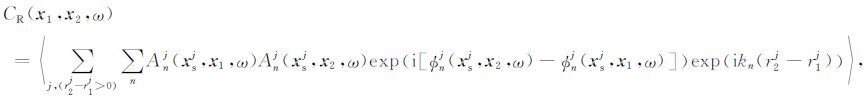
|
(7) |
左行波
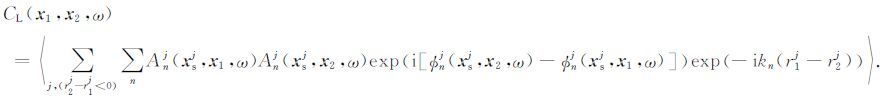
|
(8) |
把激发右行波的震源进一步分成两部分,一部分位于台站1左方的两台站连线上.考虑到面波的敏感区[15~17],这些震源应该位于图 1中两台站连线的左方灰度区(称为右行波有效震源区),在此条件下两观测点相对于震源的方位角相同,所以Φnj(xsj, x2,ω)=Φnj(xsj, x1,ω),r2j -r1j =Δ (两台站之间的距离).另一部分为剩下的震源.右行波相关函数可表为
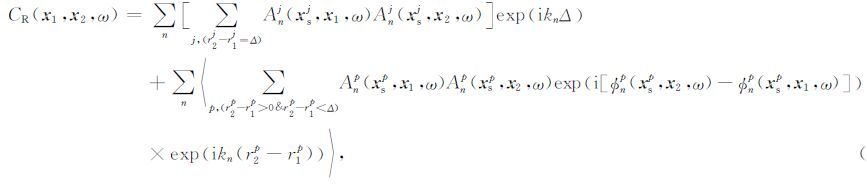
|
(9) |
其中上角标j对图 1中两台站连线的左方灰度区内的震源求和.上角标p对激发右行波的其他震源求和.对于p求和的震源满足条件r2p -r1p Δ (参考图 1).令
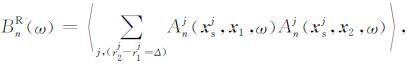
|
(10) |
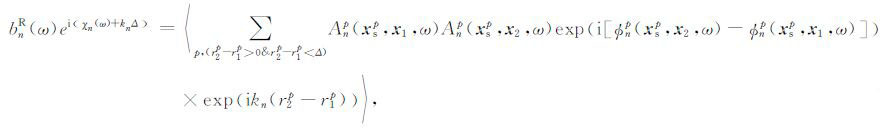
|
(11) |
将(10),(11)式代入(9)式得到
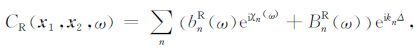
|
(12) |
令
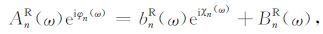
|
(13) |
带入(12)式得
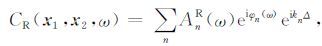
|
(14) |
对左行波作相似的处理得
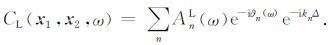
|
(15) |
表达式(14)、(15)为NCF 的面波理论表达形式.(14)与(2)式比较可知,NCF 等价于面波的激发,其中一个观测点为等价震源点,φn(ω)与n(ω)为等价震源的相位.在噪声源非均匀分布的条件下,右行波(14)式与左行波(15)式肯定是非对称的.
3 频散测量的误差实际资料测量表明,相关函数(14)、(15)式保留了两台站之间真实的面波频散信息,从中提取的群速度频散与利用地震路径提取的群速度频散相同.遵从实测资料类似的处理方法,对右行波(14)式作简化的时频分析,即对(14)式作以中心频率为ω0 的窄通滤波,为书写方便去掉振型的角标,并且只针对基阶振型,得
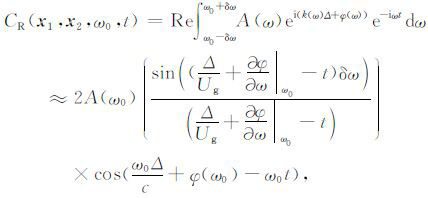
|
(16) |
上式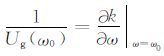
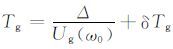
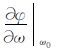
由群速度走时误差定义得
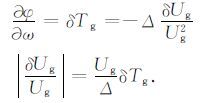
|
(17) |
假设δTg =ε(ω)T(走时误差小于一个波长),0<ε(ω)<1,T为周期,代入(17)式得
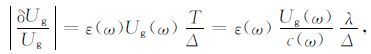
|
(18) |
其中c为相速度,λ 为波长.ε(ω)由实际测量决定.群速度的测量误差与两台站之间的距离成反比与周期成正比.
以上分析表明φn(ω)和vn(ω)是群速度和相速度测量误差的根源.出于这样的原因可把表达式(10)称为信号项,而把(11)式称为噪声项.除非已知震源分布,否则我们不可能从理论上准确的计算出φn(ω)和vn(ω)的值,它们必须由实际资料的测量来决定.
由(13)式可得
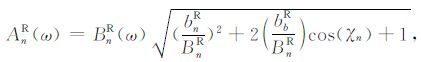
|
(19) |
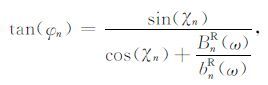
|
(20) |
当信噪比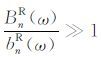
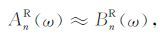
|
(21) |
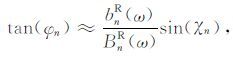
|
(22) |
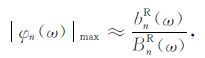
|
(23) |
φn的取值范围为
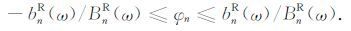
|
在大信噪比的条件下,由(23)式可以计算出相速度测量的最大相对误差.假设用基阶右行波测量相速度,根据(14)式,其谐波表达形式为
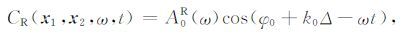
|
(24) |
令φ0 +k0Δ-ωt=0,则
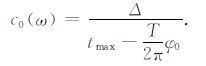
|
(25) |
其中t=tmax 为谐波波峰到时.根据(25)式可得到相速度的相对误差:
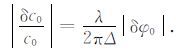
|
(26) |
在大信噪比条件下,δφ0 ~φ0,最大相对误差为
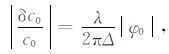
|
(27) |
由(23)式得
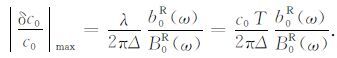
|
(28) |
相速度测量误差与周期成正比,与两台间的距离成反比,与信噪比成反比.这一结论与传统的双台法测量相速度的结论完全相同[18].
4 关于等价震源相位φn的讨论噪声项(11)式中的求和是振荡型的,理想的震源分布可能使其为零或者与信号项相比很小.但是,当波长λn >Δ 时,这些低频噪声是无论如何不能通过叠加相消的.这是因为,
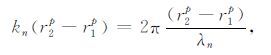
|
当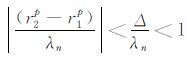
对于特殊的噪声震源分布,表达式(11)代表的噪声相也有可能表现为相长叠加.比如,噪声源分布在某一个优势方位上.遵从同样的群速度分析,噪声项(11)的波包应该在信号波包之前到达.
如果假设两台站地震背景噪声的互相关函数的负导数(经验格林函数)等价于两台站之间介质的格林函数,即iωCR(x1,x2,ω)~ G(x1,x2,ω),可推得φn(ω)=-π/4.
不同的噪声源分布,可得到不同的等价震源相位谱.理论上可以设计出0~2π之间变化的任意等价震源相位函数.在噪声源全部分布在两台站连线的有效震源区(图 1 中的灰度区)的极端条件下,φn=0,vn=0.所以,φn和vn并不是简单的常数,它们的值依赖于噪声源的分布条件.无论采取何种假设(或何种设计),都不会对群速度测量产生很大的影响.但是,不能因为群速度测量的成功就认为等价格林函数假设对于相速度的测量同样适用.虽然我们给不出φn和vn的具体表达式,但在大信噪比的条件下,我们能够估计出它们的最大可能取值.
5 三台法求相速度初讨以上研究表明,在噪声源非均匀分布的条件下,右行波(假设为因果波形)的等价震源相位φn与左行波(假设为非因果波形)的等价震源相位vn并不相等.但在群速度的测量中都是将因果波形与非因果波形简单相加后进行测量,以提高信噪比.既然φn与vn不相等,这种简单相加的正确性就缺乏理论上的保证,尤其在相速度的测量中值得商榷.以下假设右行波为高信噪比的波形,我们用其来测量基阶面波相速度.
选择三个近乎在同一大圆弧上背景噪声观测记录,依序标记为台站1,台站2,台站3.设台站1与台站2 的距离为Δ12,台站2 与台站3 的距离为Δ23,台站1与台站3的距离为Δ13.由公式(25)得到台站1与台站2的相速度走时为
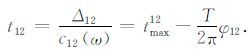
|
(29) |
其中c12(ω)为相速度,φ12 为等价震源相位,tmax12 为谐波波峰到时.同样可以得到台站2与台站3的相速度走时,以及台站1与台站3的相速度走时
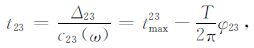
|
(30) |
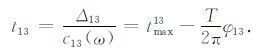
|
(31) |
由于三个台站在一条直线上,所以必须满足下列条件
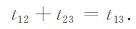
|
(32) |
将(29)~(31)式代入(32)式得到
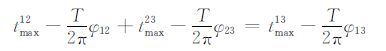
|
化简后得到
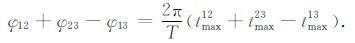
|
(33) |
在高信噪比的条件下,由(23)式可知|φij|$\ll $1,所以,在实际测量中,第一次测量相速度时可假设φij=0,得到tmaxij 的值.将tijmax 的值代入(33)式,并假设φ12 ≈φ23 ≈φ13,得到
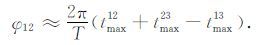
|
(34) |
将依据(34)式求得的等价相位φ12 代入(25)式,求得c12(ω)的修正值.
实际问题中有时很难满足条件(32)式,一般情况是Δ12 +Δ23>Δ13,即三个台站不是严格的在一条直线上.令Δ12 +Δ23 -Δ13 =δ,由此引起的时差约为dt≈δ/[(c12+c13)·0.5],表达式(32)式修正为

|
(35) |
公式(34)式修正为
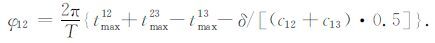
|
(36) |
将依据(36)求得的等价震源相位φ12 代入(25)式,求得c12(ω)的修正值.
公式(36)可用于实测验证等价格林函数假设的正确与否,即φn(ω)是否等于常量-π/4.Fan-ChiLin 等[19]研究了美国西部的统计结果,得出φn(ω)的均值为-π/4.实际上,所有方位上的统计平均与噪声源均匀分布的假设并无区别,得到-π/4的结论并不奇怪.这与不同方位φn(ω)的值可能不同的结论并不矛盾.理论分析表明,在利用NCF 研究区域横向非均匀时必须考虑φn(ω)的方位依赖性,以此得出更为精确的反演结果.设某一方位的统计平均为珔φn(ω),则δφ ≈φ12 -珔φn(ω),代入(26)式可估算出该方位实测相速度的统计误差.
6 结论本文从弹性动力学面波激发表达式出发,假设统计意义上不同震源的记录相互独立,不同模式之间相互独立,推导出NCF 的面波理论表达形式(21)和(22),并证明了NCF等价于面波震源激发,其中一个观测点为等价震源点.它们能够解释NCF的时空不对称性.等价震源相位φn和vn与噪声源的分布有关,在均匀分布的条件下,它们等于-π/4.大信噪比条件下φn和vn的最大可能取值为信噪比的倒数.一般情况下它们并不等于简单的常数.本文给出了三台法估算φn和vn的方法以及估算相速度测量误差的公式,据此可测量出更为精确的相速度.
| [1] | Weaver R L, Lobkis O I. Ultrasonics without a source: Thermal fluctuation correlation at MHz frequencies. Phys. Rev. Lett , 2001, 87(13): 134301. |
| [2] | Lobkis O I, Weaver R L. On the emergence of the Green's function in the correlations of a diffuse field. J. Acoust. Soc. Am , 2001, 110(6): 3011-3017. |
| [3] | Weaver R L, Lobkis O I. Diffuse fields in open systems and the emergence of the Green's function (L). J. Acoust. Soc. Am , 2004, 116(5): 2731-2734. |
| [4] | Shapiro N M, Campillo M. Emergence of broadband Rayleigh waves from correlations of the ambient seismic noise. Geophys. Res. Lett , 2004, 31: L07614. DOI:10.1029/2004GL019491 |
| [5] | Roux P, Sabra K G, Kuperman W A, et al. Ambient noise cross correlation in free space: theoretical approach. J. Acoust. Soc. Am , 2005, 117(1): 79-84. |
| [6] | Sabra K G, Gerstoft P, Roux P, et al. Extracting time-domain Greens function estimates from ambient seismic noise. Geophys. Res. Lett , 2005, 32: L03310. DOI:10.1029/2004GL021862 |
| [7] | Sabra K G, Gerstoft P, Roux P, et al. Surface wave tomography from microseisms in Southern California. Geophys. Res. Lett , 2005, 32: L14311. DOI:10.1029/2005GL023155 |
| [8] | Shapiro N M, Campillo M, Stehly L, et al. High-resolution surface-wave tomography from ambient seismic noise. Science , 2005, 307(5715): 1615-1618. DOI:10.1126/science.1108339 |
| [9] | Campillo M, Paul A. Long-Range correlations in the diffuse seismic coda. Science , 2003, 299(5606): 547-549. DOI:10.1126/science.1078551 |
| [10] | Paul A, Campillo M, Margerin L, et al. Empirical synthesis of time-asymmetrical Green functions from the correlation of coda waves. J. Geophys. Res , 2005, 110: B08302. DOI:10.1029/2004JB003521 |
| [11] | Yang Y J, Ritzwoller M H, Levshin A L, et al. Ambient noise Rayleigh wave tomography across Europe. Geophys. J. Int , 2007, 168: 259-274. |
| [12] | Yao H J, van der Hilst R D, de Hoop M V. Surface-wave array tomography in SE Tibet from ambient seismic noise and two-station analysis: I—Phase velocity maps. Geophys. J. Int , 2006, 166(2): 732-744. |
| [13] | Snieder R. Extracting the Green's function from the correlation of coda waves: a derivation based on stationary phase. Phys. Rev. E , 2004, 69(4): 046610. |
| [14] | Aki K, Richards P G. Quantitative Seismology. San Francisco: W. H. Freeman, 1980. 314 |
| [15] | Yoshizawa K, Kennett B L N. Determination of the influence zone for surface wave paths. Geophys. J. Int , 2002, 149(2): 441-454. |
| [16] | Spetzler J, Trampert J, Snieder R. The effect of scattering in surface wave tomography. Geophys. J. Int , 2002, 149(3): 755-767. |
| [17] | Zhou Y, Dahlen F A, Nolet G. Three-dimensional sensitivity kernels for surface wave observables. Geophys. J. Int , 2004, 158(1): 142-168. |
| [18] | Aki K, Richards P G. Quantitative Seismology, vol. 1. San Francisco: W. H. Freeman, 1980. 581 |
| [19] | Lin F C, Moschetti M P, Ritzwoller M H. Surface wave tomography of the western United States from ambient seismic noise: Rayleigh and Love wave phase velocity maps. Geophys. J. Int , 2008, 173(1): 281-298. |
 2011, Vol. 54
2011, Vol. 54

