2. 中国地震局地质研究所,北京 100029;
3. 中国科学技术大学地球与空间科学学院,合肥 230026;
4. 北京大学地球与空间科学学院,北京 100871
2. Institute of Geology, China Earthquake Administration, Beijing 100029, China;
3. School of Earth and Space Sciences, University of Science and Technology of China, Hefei 230026, China;
4. School of Earth and Space Sciences, Peking University, Beijing 100871, China
传统震源的研究均假设断层区(Faultzone)为各向同性介质[1~9],然而过去30多年横波分裂的理论、观测和实验均证实地球介质在不同程度上是各向异性的[10~22].Crampin 等众多的研究成果表明,在地壳和上地幔广泛存在着与应力敏感的含液体饱和裂隙或孔隙,其在整体上呈现出方位各向异性的特征[14];与此同时,传统的各向异性研究均集中于传播路径上的各向异性[23~26],而较少关注于震源区的各向异性,既然地壳和上地幔广泛存在着与应力敏感的含液体的裂隙或孔隙,那么将震源区假定为各向异性介质是合理的;此外,断层区作为应力较为集中的区域,岩石较为破碎,速度相对于断层周围的岩石要低[27],在整体上呈现各向异性的特征也是符合实际野外地质调查的;从地震发生的机理上看,地震的成核和扩展主要发生在断裂带上且与断层区的应力状态息息相关,而断层区的裂缝对应力变化较为敏感,因此如果能对震源区的各向异性参数做系统详细的研究则对于探索地震的发生无疑具有重要的意义.
一般来讲,震源的研究主要涉及点源表述、点源辐射、震源运动学和震源动力学[28, 29].就各向异性震源研究的历史来讲,其研究主要集中于各向异性点源辐射问题[26, 30~32],其假设震源区是各向同性介质,而传播介质则考虑为各向异性介质,如Ben-Menahem、姚陈以及Gajewski在20世纪90年代的研究工作[26, 30~32].但当震源区和传播介质均为各向异性时,地震波的激发和传播有何新的特征,如何通过地震数据去获取震源区各向异性参数,目前并没有获得清楚的认识,然而要弄清楚这些问题,首先就要知道描述各向异性点源的地震矩张量.
将震源区假设为各向异性介质的研究起始于2004年捷克人Vavrycuk 及其研究团队的工作,他们研究了各向异性介质下几个特殊断层面剪切位错源的地震矩张量并从数学上确认了各向异性源本身是造成非双力偶机制的一个重要原因[33~36].但是他们并没有给出任意断层取向下,剪切位错源和张裂源的解析表达式.
ATI介质(Transversely isotropic media with arbitrary orientation axis of symmetry)是具有任意空间取向的横向各向同性介质,其对称轴在空间地理坐标系下可任意取向[37~40].姚陈和蔡明刚[37]给出了任意空间取向TI介质(ATI)四阶弹性张量解析表达式,该表达式具有唯一性、完备性、简洁性和物理意义明确的特点.尽管在此之前,德国学者Spies[41]已给出类似的表达式,但不便用于矩张量的研究.在姚陈和蔡明刚[37]工作的基础上,将ATI介质弹性张量解析表达式运用到各向异性地震矩张量的研究,并给出了剪切位错源矩张量解析表达式,为后续各向异性震源反演的研究奠定了理论基础.
本文首先给出了各向异性ATI介质剪切位错源地震矩张量解析表达式,然后讨论了各向同性分量的物理意义,还用一些例子来说明各向异性对双力偶分量(DC)、各向同性分量(ISO)和补偿线性偶极子分量(CLVD)的影响;最后讨论了各向异性剪切位错源对远场P波辐射花样和震源球的影响.
2 各向异性ATI介质地震矩张量如果所观测的地震波波长远远大于震源所涉及的尺度,则该震源可以看成地震点源[28, 29],利用点源的叠加可合成有限尺度的运动源[42~44],因此地震点源是震源研究的基础,其最一般的表述是地震矩张量(本文地震矩张量均是指二阶张量,不涉及高阶矩张量).除了少数震源[45],大部分震源无论是剪切位错源(Shear faulting)、张裂源(Tensile faulting)还是体积源(Volume source)均可以用地震矩张量来表达[28, 29, 46],其并不预先假定断层是否存在,因此地震矩张量可用来表示许多类型的震源,如天然地震、火山地震、矿震、声发射源、地下核爆破源和水力压裂源等.Aki和Richards[28, 29]给出了断层震源地震矩密度张量的定义:

|
(1) |
其中:ui代表穿越断层区的位移间断分量,υj代表断层面的法向分量,cijpq代表震源区(Faultzone)的弹性常数[28, 29],即(1)式对任意各向异性介质都是成立的.
如果震源区为各向同性介质,四阶弹性张量cijpq可以表述为[28, 29]
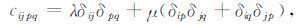
|
(2) |
将(2)式代入到(1)式,即可得到各向同性介质下地震矩张量解析表达式[28, 29]:
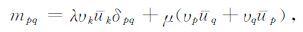
|
(3) |
如果是沿着断层面纯剪切错动,则有v·u- =0,于是
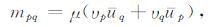
|
(4) |
式(4)代表着各向同性介质情况下剪切位错源地震矩密度张量的解析表达式.
姚陈和蔡明刚[37]给出了空间地理坐标系下,任意空间取向横向各向同性介质(ATI)弹性常数解析表达式:
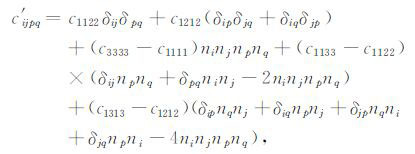
|
(5) |
其中c1122,c1212,c3333,c1111,c1133 是TI介质固有的5个独立弹性常数[36],n= (n1,n2,n3)代表ATI对称轴在空间地理坐标系下的方向余弦,其中:

|
θ和φ 分别是指ATI介质对称轴在地理坐标系下的极角和方位角.关于(5)式的详细讨论见姚陈和蔡明刚[37].将(5)式代入(1)式得到ATI介质矩密度张量表达式:
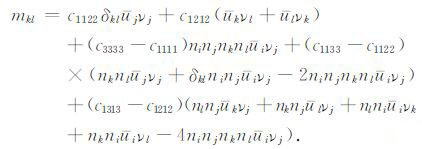
|
(6) |
大部分浅层的天然地震可看成剪切位错源,因此有ujνj=0,于是(6)式可整理为
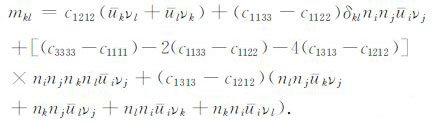
|
(7) |
为了后续研究问题的方便,对(7)式中弹性常数的组合定义为

|
(8) |
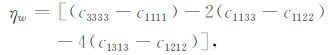
|
(9) |
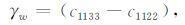
|
(10) |
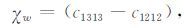
|
(11) |
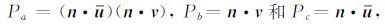
|
(12) |
从(12)式可看到,Pb代表断层面法向在ATI介质对称轴方向的投影;Pc代表断层面的滑动矢量在ATI介质对称轴方向的投影;Pa代表上述两投影的乘积.
对(7)式中相关量进行展开,并充分利用(12)式,于是有:
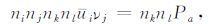
|
(13) |
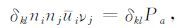
|
(14) |
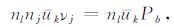
|
(15) |

|
(16) |
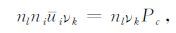
|
(17) |
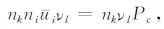
|
(18) |
最后得到ATI介质剪切位错源地震矩张量的解析表达式为
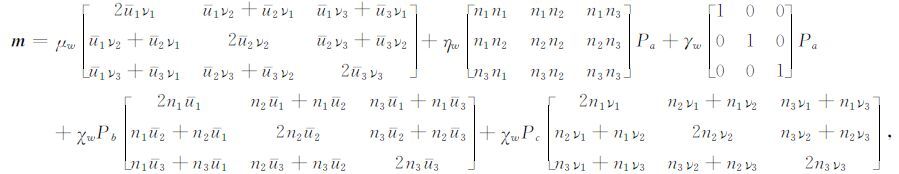
|
(19) |
(19) 式第一项代表各向异性矩张量的各向同性震源部分,其仅与断层面的位置有关;第二、三、四和五项代表震源区的各向异性对矩张量的扰动,不仅与断层面的位置有关,还与震源区各向异性对称轴取向、震源区各向异性强弱有关,而且在断层面法向矢量、断层滑动矢量和各向异性对称轴之间存在着相互耦合关系.
下面给出了一个例子.假设断层面法向矢量为ν = (0,0,1),滑动矢量u= (u1,0,0),于是ATI介质矩密度张量为
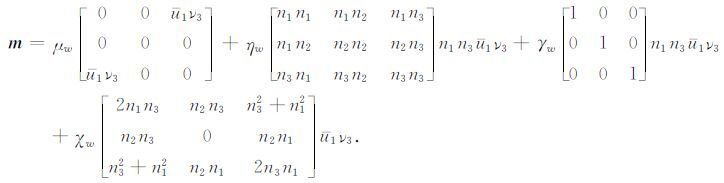
|
(20) |
假设震源区是HTI介质且n=(1,0,0),其地震矩密度张量为
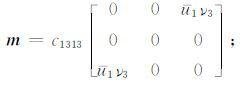
|
(21) |
假设震源区是VTI介质,n=(0,0,1),于是

|
(22) |
假设震源区是方位为φ 的HTI介质,即n= (cosφ,sinφ,0),则有
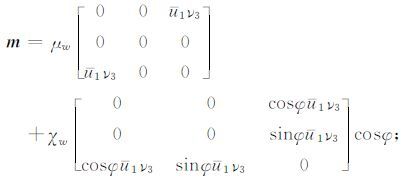
|
(23) |
当震源区是倾斜TI介质且对称轴处于空间地理坐标系下XOZ平面时,假设n= (sinθ,0,cosθ),于是
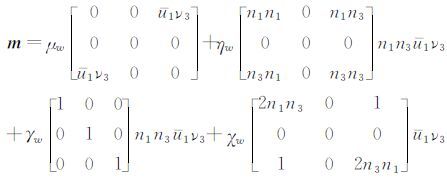
|
(24) |
由(19)式可得到矩密度张量各向同性分量(isotropiccomponent)解析表达式
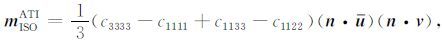
|
(25) |
(25) 式显示:矩密度张量各向同性分量mISOATI 可以表达成三项的乘积,第一项是弹性常数的组合$\frac{1}{3}$(c3333 -c1111 +c1133 -c1122);第二项是断层面上的滑动矢量在对称轴方向上的投影($\dot{n}$u),其量纲为位移;第三项是断层面法向在ATI对称轴方向上的投影($\dot{n}$v),为无量纲量.根据(20)式可知mISOATI =0时需满足
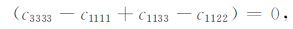
|
(26) |
即震源区为各向同性介质时(或某些特殊各向异性时),或者
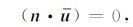
|
(27) |
即n⊥u,即ATI介质对称轴垂直于断层面.
或者
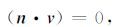
|
(28) |
即n⊥v,即ATI介质对称轴垂直于断层面法向.
即震源区为各向同性介质或者断层面处于ATI介质对称平面时,剪切位错源会造成各向同性分量为0.
当不满足(26),(27)和(28)式中任意一条时,矩密度张量各向同性分量为
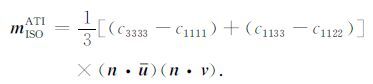
|
根据地震矩张量和密度张量之间的关系

|
(29) |
(29) 式中的ΔViso 代表由于震源区各向异性介质条件下剪切错动所造成沿着对称轴方向上的体积变化.于是
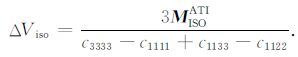
|
(30) |
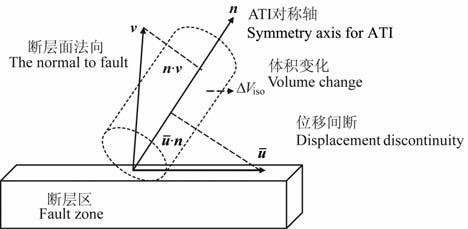
图 1给出了(29)式的物理意义.
|
图 1 ATI介质纯剪切错动产生对称轴方向上的体积变化示意图 Fig. 1 The cartoon of volume change along symmetry axis due to shear faulting in ATI earthquake source |
由(25)式可知,若知道各向同性分量、断层面和对称轴之间的关系,就可以反演出断层区的弹性常数组合c3333-c1111+c1133-c1122,若震源区的各向异性是由单组裂缝导致,则有
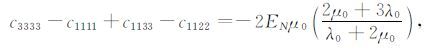
|
(31) |
其中EN为裂隙的法向弱度,其与裂隙密度、纵横比和裂隙填充物质有关;λ0 和μ0 是震源区各向同性母体岩石的拉梅常数,因此有可能通过矩张量的各向同性分量获得震源区裂隙的信息.
如果将震源区的各向异性用Thomsen参数ε,δ和γ 来表述[47],则矩密度张量之各向同性部分表示为
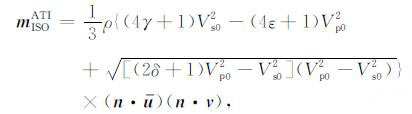
|
(32) |
其中Vp0和Vs0代表震源区各向同性背景岩石弹性常数.由(32)式可知,假设断层面和ATI介质的对称轴固定,则各向同性分量与各向异性参数ε 和γ成线性关系,且Thomsen参数ε、δ和γ 越大,各向同性分量的绝对值也越大;当ε=δ=γ =0即各向同性介质时,有c3333 -c1111 +c1133 -c1122 =0,此情形下,各向同性分量为0.
3 各向异性对DC、ISO 和CLVD 百分比含量的影响国际上,一般用DC、ISO 和CLVD 百分比含量衡量非双力偶程度.首先进行矩张量分解,就分解方法而言,可分为主坐标系下的分解和空间地理坐标系下的分解,国际上[37]一般在主坐标系下分解成双力偶部分(DC)、各向同性分量部分(ISO)和补偿线性偶极子部分(CLVD).假设反演得到了地震矩张量为M,求矩阵M的特征值和特征向量,设其特征值为M1、M2 和M3,则各向同性分量为
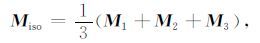
|
于是有[48]:

|
(33) |
在(33)式中右边第二项代表偏量部分(DC+CLVD),对于偏量部分(Deviatoric)有多种分解结果[46],本文只讨论关于DC 和CLVD 的分解.需要说明的是,对于(33)式中的偏量部分,有|M1|≤ |M2|≤|M3|和|M1*|≤|M2*|≤|M3*|[48],按照Knopoff和Randal的思想[49]即将CLVD 的主轴与DC 的主轴一致,于是有:
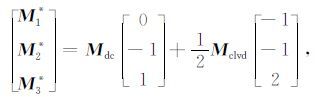
|
(34) |
其中
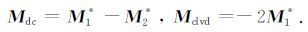
|
为了描述偏量部分偏离双力偶分量的程度,定义了一物理量εd[34, 48, 50],为了避免与上面的Thomsen参数混淆,我们用εd表示CLVD相对于DC的大小:
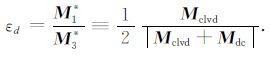
|
(35) |
当εd=0时,代表纯双力偶机制;当εd=±$\frac{1}{2}$,代表纯CLVD 机制.此外εd取正值代表CLVD 的主偶极子呈现拉张极性;负值代表CLVD 的主偶极子呈现压缩极性.
为了计算ISO、DC 和CLVD 在地震矩张量中的百分含量,有下面的定义[34]
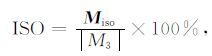
|
(36) |
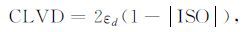
|
(37) |

|
(38) |
在(36)、(37)式和(38)式中,ISO 和CLVD 可正可负,其中ISO>0 代表体积膨胀,相反ISO<0 代表体积压缩;而CLVD 的正负由εd来控制;DC 为正.
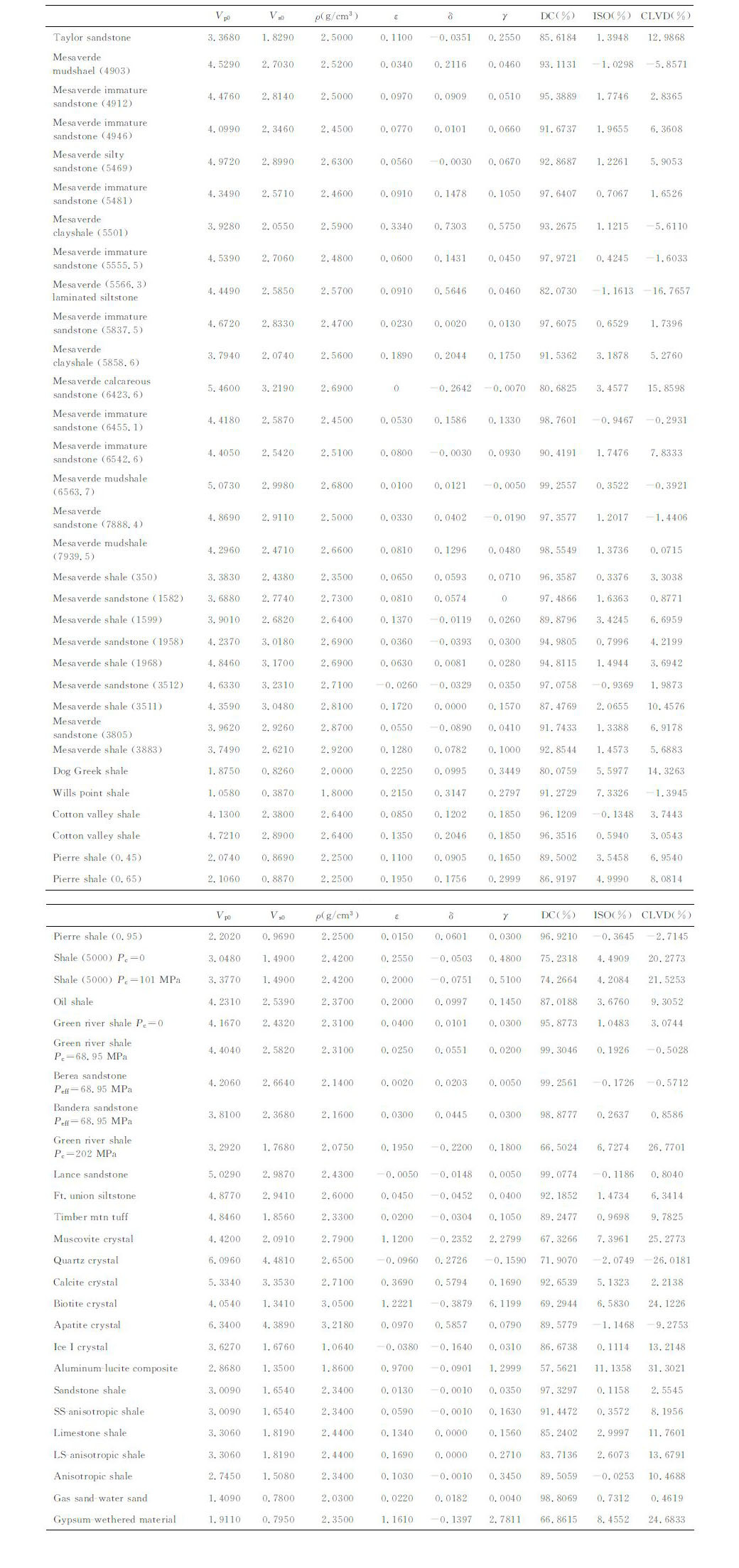
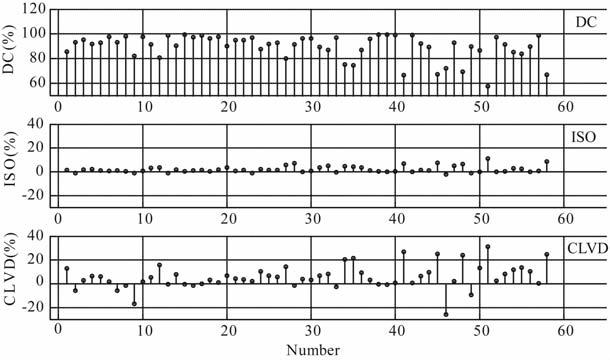
为了实际说明各向异性参数对ISO、DC 和CLVD 在地震矩张量中的百分含量之影响,本文选用发生在2008年5月12日14点28分的汶川地震主震之断层面解[51]作为数值计算的例子,其具体计算参数为:断层面走向231°、断层面倾角35°以及断层面滑动角138°;此外参考石玉涛、高原等人关于汶川地震震源区剪切波分裂的结果[52],假设汶川地震主震震源区ATI介质对称轴倾角55°,方位角为141°.至于各向异性参数,类似于Vavrycuk[35]的做法,本文选用Thomsen[47]发表的上地壳沉积盆地岩石(少量材料学中参数)弱各向异性数据(表 1).需要指出的是:尽管沉积盆地的岩石各向异性参数与天然地震震源区各向异性参数有所不同(深度、温度和压力均不同),但考虑到主要目的是粗略了解各向异性与非双力偶机制之间的关系,在没有震源区真实的各向异性数据情况下,选择Thomsen发表的各向异性数据[47]也是一种较好的选择[35].有了上述参数,根据(19)式、(36)式至(38)式就可计算DC、ISO和CLVD 百分含量(表 1).从表 1数值实验结果以及图 2之DC、ISO 和CLVD 百分含量散点图显示,DC 大部分处于80%~100%之间,ISO 绝大部分都处于10%以下,除了一个“事件",即当震源区各向异性结构是Aluminum-lucitecomposite 时(见表 1),其各向异性较强,ISO 可达到11%,此外另外一个各向异性材料Muscovitecrystal(白云母晶体),各向异性也较强,也会产生比较大的ISO 分量(7%)和CLVD 分量(25%).表明在纯剪切错动的机制下,使用Thomsen[47]发表的上地壳岩石弱各向异性数据,数值模拟得到的“汶川地震矩张量"的各向同性分量一般不会超过10% ,但实际汶川地震主震地震矩张量解的各向同性分量高达39%、CLVD分量达到了-35%,而双力偶分量只有25%(根据陈运泰院士研究组地震矩张量反演结果计算[51]),如此强的非双力偶分量的原因可能有两点:第一,汶川地震震源区各向异性较强,因此纯剪切错动可能产生较大的ISO 分量和CLVD 分量;第二,从现有反演结果上看,汶川地震主震断层为“铲状"断层面[53],在这种非平断层面上错动很有可能含有张裂机制,从我们目前的工作来看,即使很微小角度的偏离断层面错动,也会产生较大的非双力偶分量[54],因此,本模拟从一个侧面也说明汶川地震发震断层几何复杂性.
|
|
表 1 上地壳岩石和部分材料各向异性参数[47]以及DC、ISO和CLVD百分比之结果 Table 1 Anisotropic parameters for some rocks in the crust[47] and the percent result of DC,ISO,and CLVD |
|
图 2 DC、ISO 和CLVD 百分含量散点图 Fig. 2 The percent scatter diagram of DC,ISO,and CLVD |
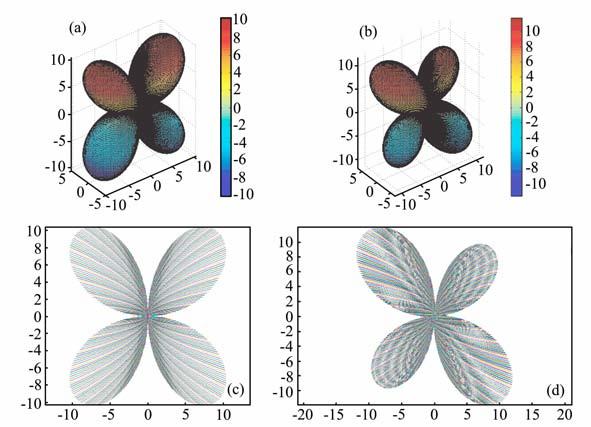
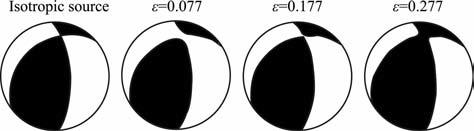
依照前面地震矩张量的解析表达,然后利用Aki和Richards[28]给出的表达式(P111,4.96)计算远场P波辐射花样.需要说明的是,这样的做法假定了传播介质是全空间各向同性而震源区是各向异性的.如图 3所示,假设震源区岩石P波速度为4.099km/s, S波速度为2.346km/s, 密度为2.45g/cm3,断层面走向0°、断层面倾角0°以及断层面滑动角0°(Aki和Richards[29],P43,Figure 3.2),图 4a和图 4c分别给出了各向同性震源下的P 波三维远场辐射图案和对应的XOY平面远场辐射图案;图 4b 和图 4d分别给出了各向异性(数据来自于Thomsen[47],ε=0.077,δ=0.01 和γ=0.066,ATI对称轴倾角55°,对称轴方位角141°)震源下的P波三维远场辐射图案和对应的XOY平面远场辐射图案.图 4 显示,各向同性剪切位错震源,远场P 波辐射花样四象限对称分布,而各向异性剪切位错震源,远场P波辐射花样并不是四象限对称分布,而这种不对称性可反映在震源球上.Aki和Richards[28, 29]给出了下半球等面积投影震源球的画法,依据此方法并结合图 4中远场P 波辐射的结果,本文模拟了各向异性剪切位错源之震源球.假设断层面方位角Φs=231°,断层面倾角δ=35°,滑动角λ=138°,此外震源区各向同性背景岩石纵波速度Vp=4.099km/s, 横波速度Vs=2.346km/s, 岩石密度ρ=2.45g/cm3,裂隙倾角55°,裂隙方位角141°,各向异性参数部分,假设Thomsen参数为δ=0.01 和γ=0.0667 保持不变,ε可变且分别取0.077,0.177 和0.277,图 5模拟了不同震源各向异性情形下的震源球.结果表明,当震源区是各向同性介质时,震源球两节线是相交的;但当震源区为各向异性时,其导致了震源球节线不相交,从而显示各向异性是非双力偶机制的重要原因.
|
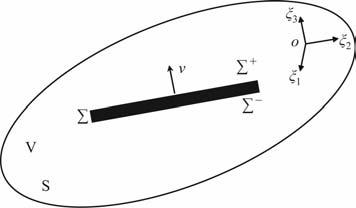
图 3 断层震源示意图 V 代表地球体,S代表地球表面,黑色长条代表断层区,Σ+ 代表断层上界面,Σ- 代表断层下界面,ν代表断层面法向,o-ξ1ξ2ξ3代表震源坐标系. Fig. 3 The cartoon of fault source A finite elastic anisotropic body, with volume V and external surface S,and internal surface 2,and black rectangle is fault zone, s the positive side of the fault and Σ一 s the oppositeside of fault.The normal to Σ is v and 0-ξ1ξ2ξ3 s epicenter coordinate syst |
|
图 4 剪切位错震源远场P波辐射花样 (a, c)是各向同性剪切位错源,(b, d)是各向异性剪切位错震源. Fig. 4 The far-iield P- wave radiation pattern from shear dislocation (a, c) Shear dislocation in isotropic media; (b, d) Shear dislocation in anisotropic media. |
|
图 5 各向异性对震源球的影响 Fig. 5 Anisotropic effect on focal sphere |
本文详细讨论了ATI介质剪切位错震源地震矩张量解析表达以及各向异性对非双力偶机制的影响.得到如下结论:
(1) 即使纯剪切错动仍然产生各向同性分量,其物理意义是沿着ATI介质对称轴方向产生体积变化.但是当断层面位于ATI介质对称平面时,纯剪切错动不会产生各向同性分量,其仍然可以看成双力偶机制.此外各向异性强弱、各向异性对称性和断层面的位置都影响着非双力偶分量,解析的各向异性地震矩张量表述显示非双力偶分量提供了探测震源区各向异性结构的信息.
(2) 以矩张量反演得到的汶川地震主震断层面解为例,通过数值模拟认识到,弱各向异性介质下的纯剪切位错震源,各向同性分量一般不会超过10%,CLVD分量可能达到30%,而DC 分量大致在80%~100%之间.
(3) 考虑震源为各向异性而传播介质为全空间各向同性时,剪切位错源P 波远场辐射花样四花瓣不再对称,震源球两节线不再相交.
总之,各向异性矩张量能提供震源区更多的信息;相比于其他探测各向异性的方法,通过各向异性矩张量方法直接提供的是震源区各向异性的信息,就监测地震而言,提取震源区各向异性信息可能有利于了解地震是如何成核、破裂和扩展的,因此研究各向异性地震矩张量具有重要的价值和应用前景.下一步进行各向异性地震矩张量的反演还需考虑一系列问题,比如如何选取正演计算所需的震源模型和全球或者区域各向异性结构模型以及在考虑各向异性情形下,如何对区域性震相和远震震相进行波形模拟.
致谢感谢匿名评审人对本文提出的建设性建议.
| [1] | Gilbert F, Dziewonski A M. An application of normal mode theory to the retrieval of structural parameters and source mechanisms from seismic spectra. Philos. Trans. R. Soc., Ser. A , 1975, 278(1280): 187-269. |
| [2] | Fitch T J, McCowan D W, Shield M W. Estimation of the seismic moment tensor from teleseismic body wave data with applications to intraplate and mantle earthquakes. J. Geophys. Res , 1980, 85(B7): 3817-3828. |
| [3] | Dziewonski A M, Chou T A, Woodhouse J H. Determination of earthquake source parameters from waveform data for studies of global and region seismicity. J. Geophys. Res , 1981, 86(B4): 2825-2852. |
| [4] | Dziewonski A M, Woodhouse J H. An experiment in the systematic study of global seismicity: centroid-moment tensor solution for 201 moderate and large earthquakes in 1981. J. Geophys. Res , 1983, 88: 3247-3271. |
| [5] | Dreger D S, Helmberger D V. Determination of source parameters at regional distances with three-component sparse network data. J. Geophys. Res , 1993, 98(B5): 8107-8125. |
| [6] | Sipkin S A. Estimation of earthquake source parameters by the inversion of waveform data: synthetic waveforms. Physics of the Earth and Planetary Interiors , 1982, 30(2-3): 242-259. DOI:10.1016/0031-9201(82)90111-X |
| [7] | Minson S, Dreger D S. Stable inversions for complete moment tensors. Geophys. J. Int , 2008, 174: 585-592. |
| [8] | Chen Y T, Xu L S, Li X, et al. Source process of the 1990 Gonghe, China, earthquake and tectonic stress field in the northeastern Qinghai-Xizang (Tibetan) plateau. Pure Appl. Geophys , 1996, 146(3-4): 697-715. |
| [9] | Kawakatsu H. Insignificant isotropic component in the moment tensor of deep earthquakes. Nature , 1991, 351(6321): 50-53. DOI:10.1038/351050a0 |
| [10] | Crampin S. A review of wave motion in anisotropic and cracked elastic-media. Wave Motion , 1981, 3(4): 343-391. DOI:10.1016/0165-2125(81)90026-3 |
| [11] | Booth D C, Crampin S. The anisotropic reflectivity technique: theory. Geophys. J. R. Astron. Soc , 1983, 72(3): 755-766. |
| [12] | Crampin S. Effects of point singularities on shear-wave propagation in sedimentary basins. Geophys. J. R. Astron. Soc , 1991, 107(3): 531-543. |
| [13] | Crampin S, Peacock S. A review of the current understanding of seismic shear-wave splitting in the Earth's crust and common fallacies in interpretation. Wave Motion , 2008, 45(6): 675-722. DOI:10.1016/j.wavemoti.2008.01.003 |
| [14] | Crampin S. The dispersion of surface wave in multilayered anisotropic media. Geophys. J. R. Astron. Soc , 1970, 21(3): 387-402. |
| [15] | Gao Y, Wu J. Compressive stress field in the crust deduced from shear-wave anisotropy: an example in capital area of China. Chinese Sci. Bull , 2008, 53(18): 2840-2848. |
| [16] | Wu J, Gao Y, Chen Y T. Shear-wave splitting in the crust beneath the southeast Capital area of North China. J. Seism , 2009, 13(2): 277-286. |
| [17] | Gao Y, Wu J, Cai J A, et al. Shear-wave splitting in the southeast of Cathaysia block, South China. J. Seism , 2009, 13(2): 267-275. |
| [18] | Gao Y, Wu J, Yi G X, et al. Crust-mantle coupling in North China: Preliminary analysis from seismic anisotropy. Chinese Sci. Bull , 2010, 55(31): 3599-3605. DOI:10.1007/s11434-010-4135-y |
| [19] | Chen Y, Badal J, Zhang Z J. Radial anisotropy in the crust and upper mantle beneath the Qinghai-Tibet Plateau and surrounding regions. Journal of Asian Earth Sciences , 2009, 36(4-5): 289-302. DOI:10.1016/j.jseaes.2009.06.011 |
| [20] | Liu K, Zhang Z J, Hu J F, et al. Frequency band-dependence of S-wave splitting in China mainland and its implications. Science in China (Series D) , 2001, 44(7): 659-665. DOI:10.1007/BF02875339 |
| [21] | Zhang Z J, Li Y K, Lu D Y, et al. Velocity and anisotropy structure of the crust in the Dabieshan orogenic belt from wide-angle seismic data. Physics of the Earth and Planetary Interiors , 2000, 122(1-2): 115-131. DOI:10.1016/S0031-9201(00)00190-4 |
| [22] | Zhang Z J, Teng J W, Badal J, et al. Construction of regional and local seismic anisotropic structures from wide-angle seismic data: crustal deformation in the southeast of China. J. Seism , 2009, 13(2): 241-252. |
| [23] | Crampin S. Effective anisotropic elastic-constants for wave propagation through cracked solids. Geophys. J. R. Astron. Soc , 1984, 76(1): 135-145. |
| [24] | Crampin S, Taylor D B. The propagation of surface waves in anisotropic media. Geophys. J. R. Astron. Soc , 1971, 25(1-3): 71-87. |
| [25] | Crampin S. A review of the effects of anisotropic layering on the propagation of seismic waves. Geophys. J. R. Astron. Soc , 1977, 49(1): 9-27. |
| [26] | Yao C, Xiong Y. Far-fields radiation pattern from an anisotropic dislocation point source. Can. J. Expl. Geophys , 1993, 29: 315-323. |
| [27] | Li Y G, Aki K, Adams D, et al. Seismic guided waves trapped in the fault zone of the Landers, California, earthquake of 1992. J. Geophys. Res , 1994, 99(B6): 11705-11722. |
| [28] | Aki K, Richards P G. Quantitative Seismology: Theory and Methods. San Francisco: Freeman, 1980 . |
| [29] | Aki K, Richards P G. Quantitative Seismology. California: University Science Books, 2002 . |
| [30] | Ben-Menahem A, Sena A G. The elastodynamic Green's tensor in an anisotropic half-space. Geophys. J. Int , 1990, 102(2): 421-444. |
| [31] | Ben-Menahem A, Sena A G. Green's tensor and radiation pattern of point sources in general anisotropic inhomogeneous elastic media. Geophys. J. Int , 1991, 107(2): 297-308. |
| [32] | Gajewski D. Radiation from point sources in general anisotropic media. Geophys. J. Int , 1993, 113(2): 299-317. |
| [33] | Vavrycuk V. Inversion for anisotropy from non-double-couple components of moment tensors. J. Geophys. Res , 2004, 109(B7): B07306. DOI:10.1029/2003JB002926 |
| [34] | Vavrycuk V. Focal mechanisms in anisotropic media. Geophys. J. Int , 2005, 161: 334-346. DOI:10.1111/j.1365-246X.2005.02585 |
| [35] | Vavrycuk V. Focal mechanisms produced by shear faulting in weakly transversely isotropic crustal rocks. Geophysics , 2006, 71(5): D145-D151. DOI:10.1190/1.2236378 |
| [36] | Vavrycuk V, Bohnhoff M, Jechumtálová Z, et al. Non-double-couple mechanisms of microearthquakes induced during the 2000 injection experiment at the KTB site, Germany: A result of tensile faulting or anisotropy of a rock?. Tectonophysics , 2008, 456(1-2): 74-93. DOI:10.1016/j.tecto.2007.08.019 |
| [37] | 姚陈, 蔡明刚. 任意空间取向TI弹性张量解析表述. 地球物理学报 , 2009, 52(9): 2345–2348. Yao C, Cai M G. Analytical expression of TI elastic tensor with arbitrary orientation. Chinese J. Geophys. (in Chinese) , 2009, 52(9): 2345-2348. |
| [38] | 郝重涛, 姚陈. 任意空间取向TI介质中体波速度特征. 地球物理学报 , 2007, 50(2): 546–555. Hao C T, Yao C. Analysis of body_wave velocity characteristic for TI medium with arbitrary spatial orientation. Chinese J. Geophys. (in Chinese) , 2007, 50(2): 546-555. |
| [39] | 郝重涛, 姚陈. 任意空间取向TI介质中P波四次时差系数特征. 地球物理学报 , 2008, 51(4): 1172–1179. Hao C T, Yao C. The characteristic of quartic moveout coefficient of P-wave in the TI homogeneous media with an arbitrary orientation symmetric-axis. Chinese J. Geophys. (in Chinese) , 2008, 51(4): 1172-1179. |
| [40] | 郝重涛, 姚陈. ATI介质中四次时差系数解析近似. 地球物理学报 , 2009, 52(8): 2074–2083. Hao C T, Yao C. Analytic approximation of quartic moveout coefficient in the TI media with an arbitrary spatial orientation. Chinese J. Geophys. (in Chinese) , 2009, 52(8): 2074-2083. |
| [41] | Spies M. Elastic waves in homogeneous and layered transversely isotropic media: Plane wave and Gaussian wave packets. A general approach. J. Acoust. Soc. Am , 1994, 95(4): 1748-1760. |
| [42] | Olson A H, Apsel R J. Finite faults and inverse theory with application to the 1979 Imperial Valley earthquake. Bull. Seismol. Soc. Am , 1982, 72(6A): 1969-2001. |
| [43] | 姚振兴, 郑天愉. 计算综合地震图的广义反射、透射系数矩阵和离散波数方法(二)——对不同深度点源的算法. 地球物理学报 , 1984, 27(4): 338–348. Yao Z X, Zheng T Y. A generalized reflection-transmission coefficient matrix and discrete wavenumber method for synthetic seismograms (II)-for multiple sources at different depths. Chinese J. Geophys. (Acta Geophysica Sinica) (in Chinese) , 1984, 27(4): 338-348. |
| [44] | 盖增喜, 陈晓非. 利用点源叠加合成有限尺度运动源的理论地震图. 北京大学学报(自然科学版) , 2008, 44(3): 407–412. Ge Z X, Chen X F. Point source stacking method to compute synthetic seismogram of finite moving planar source. Acta Scientianrum Naturalium Universitatis Pekinensis (in Chinese) , 2008, 44(3): 407-412. |
| [45] | Kanamori H, Given J W. Use of long-period surface waves for rapid determination of earthquake-source parameters. Physics of the Earth and Planetary Interiors , 1981, 27(1): 8-31. DOI:10.1016/0031-9201(81)90083-2 |
| [46] | 陈运泰, 吴忠良, 王培德, 等. 数字地震学. 北京: 地震出版社, 2000 . Chen Y T, Wu Z L, Wang P D, et al. Digital Seismology (in Chinese). Beijing: Seismological Press, 2000 . |
| [47] | Thomsen L. Weak elastic anisotropy. Geophysics , 1986, 51(10): 1954-1966. DOI:10.1190/1.1442051 |
| [48] | Julian B R, Miller A D, Foulger G R. Non-double-couple earthquakes 1. Theory. Reviews of Geophysics , 1998, 36(4): 525-549. |
| [49] | Knopoff L, Randall M J. The compensated linear vector dipole: A possible mechanism for deep earthquakes. J. Geophys. Res , 1970, 75(26): 4957-4963. |
| [50] | Sipkin S A. Rapid determination of global moment-tensor solution. Geophys. Res. Lett , 1994, 21(16): 1667-1670. |
| [51] | 陈运泰, 许力生, 张 勇等. 2008年5月12日汶川特大地震震源特性分析报告(http://www.csi.ac.cn/sichuan). 2008 |
| [52] | 石玉涛, 高原, 赵翠萍, 等. 汶川地震余震序列的地震各向异性. 地球物理学报 , 2009, 52(2): 398–407. Shi Y T, Gao Y, Zhao C P, et al. A study of seismic anisotropy of Wenchuan earthquake sequence. Chinese J. Geophys. (in Chinese) , 2009, 52(2): 398-407. |
| [53] | 王卫民, 赵连锋, 李娟, 等. 四川汶川8.0级地震震源过程. 地球物理学报 , 2008, 51(5): 1403–1410. Wang W M, Zhao L F, Li J, et al. Rupture process of the Ms8.0 Wenchuan earthquake of Sichuan, China. Chinese J. Geophys. (in Chinese) , 2008, 51(5): 1403-1410. |
| [54] | 蔡晓刚. 各向异性ATI介质地震矩张量理论研究. 北京: 北京大学地球物理系, 2009. Cai X G. The theoretical studies on seismic moment tensor in anisotropic ATI media (in Chinese). Beijing: the Department of Geophysics, Peking University, 2009 |
 2011, Vol. 54
2011, Vol. 54