2. 中国科学院研究生院,北京 100049
2. Graduate University, Chinese Academy of Sciences, Beijing 100049, China
重力波是传播在稳定层结大气中的一种振荡运动,是空气元受重力和各向同性热压力共同作用的结果.它的频率介于惯性频率和浮力频率之间,空间尺度处在行星尺度的运动和小尺度湍流之间[1].从狭义上定义[2],内重力波是载波介质的线性扰动,一旦产生,将沿着其射线自由传播,但非线性效应和背景可以改变其属性,使得重力波在传播过程中的特性发生变化.
大气重力波在全球的气象学、气候学、化学以及平流层和中间层的动力学中扮演着重要角色[3].重力波是全球中高层大气中最重要的动力学过程之一,来自低层大气重力波的饱和破碎形成的对中层大气的加热强度甚至会达到太阳紫外辐射的数百倍[1],而且重力波能量和动量从波源向空间的输送,对大气结构和层间耦合也有明显影响.近年来,全球大气模式成为研究大气运动的重要方法,由于重力波的尺度较小,受到计算网格的限制,在全球模式中不可能包含重力波运动,而重力波对全球大气运动又是不可忽略的,因此在全球大气模式中必须使用重力波参数化的方法来描述重力波对全球大气的影响,而从各种观测数据中得到正确描述重力波的全球分布的模型,成为构建全球大气模式的前提条件.
由于VHF雷达、MF 雷达、激光雷达等地面观测设备在世界各地相继建立[3],以及气象火箭的广泛应用[4],重力波的观测结果越来越多.然而,从这些地面台站得到的重力波特征并不能全面描述全球重力波的分布,利用卫星观测数据获取重力波信息成为了解全球重力波分布及其变化的重要手段.Fetzer和Gille[5]、Wu和Waters[6]最早使用卫星数据研究了重力波的全球分布,提出了具有较低固有频率和较长水平波长的波动导致赤道区较强重力波活动[7, 8],并分析了背景风场的影响.近年来,人们分别利用GPS/MET 的掩星数据[9]、CHAMP 的GPS掩星数据[10, 11]、Aura卫星的MLS(微波临边发生器)数据[12]、以及COSMIC GPS 掩星数据[13]分别研究了某些年份平流层重力波的全球分布特征.Krebsbach 和Preusse[14]利用SABER 多年的数据,初步研究了重力波的年、半年变化及准两年震荡(QBO).这些结果表明重力波的分布不仅随高度会发生显著变化,也会随纬度、经度和地形发生变化.例如,在冬季,重力波势能在热带和中纬度地区有较大值,而在春秋分期间,重力波只在热带区域有较强活动;从全球重力波的分布来看,两个半球的大陆地区的重力波势能都比海洋地区的重力波势能要大.虽然从这些结果可以初步认识到重力波能够由山脉的气流、对流、地形、快速斜压气流等激发产生,但是它们的具体贡献还不清楚.特别地,这些结论还不够系统,大多数工作中仅使用了较短时间的卫星数据,还不能完整地描述重力波的整体变化特征,不利于构建可靠的重力波模型.
本文利用2002年1月到2009年12月TIMED卫星上SABER 温度剖面8 年的数据,提取了可以反映重力波活动的垂直尺度在2 至10km 的中尺度温度扰动,通过分析扰动值分布特征随季节、纬度、经度和高度的变化,分析了中层大气重力波的整体分布,特别讨论了地形因素对重力波分布的影响.
2 数据与方法根据重力波能量的理论[9],设E0 是单位质量的总的重力波能量,Ek、Ep 分别为单位质量的动能和势能,则有下列关系:

|
(1) |
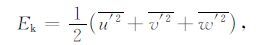
|
(2) |
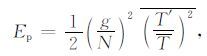
|
(3) |
其中u′、v′是风速的扰动量,分别平行和垂直于波的传播方向,w′是垂直风速.T和T′分别为温度的平均和扰动成分,g是重力加速度,N是Brunt-Vaisälä频率.根据重力波的线性理论[15],当大气重力波的频率ω 小于浮力频率N、大于惯性频率f的条件下,即f2$\ll $ω2$\ll $N2,动能和势能之比为常数.因此,温度扰动的方差就可以基本反映重力波的变化情况.
SABER 是搭载在TIMED 卫星上的一个10通道宽带辐射计,该设备在沿轨道飞行过程中采用临边探测方案获取从对流层上部直到大约130km 高度的大气辐射,在此基础上生成包括各种大气参量(温度、气压和密度等)的廓线[16].根据来自各验证报告[17, 18]的结果,在10~100km 高度范围SABER温度测量有相当高的准确性,误差平均为2~3 K.Schroeder等[19]比较了ECMWF(欧洲中期天气预报中心,European Center for Medium Weather Forecasts)综合预报系统和SABER 卫星实测数据,二者吻合得很好,例如,在南美洲的南端以及冬季极涡边缘都有明显的山脉波.与GPS 掩星观测数据比较,虽然SABER 提供的温度高度分辨率略低,但观测温度可以达到更高的高度.
对于SABER 得到的每个大气温度剖面T(z),可以看作是由背景温度剖面T(z)和扰动T′(z)组成的.假如对某个纬度带或者一个特殊观测点周边区域的所有有效数据做平均,来定义一个月平均的T(z)剖面,再将平均剖面从单个剖面中减去后得到T′(z),该扰动值有可能失真[9].因此,我们对每个剖面使用在10km 截断的高通滤波方法,得到波长在2~10km 的扰动值T′(z),从
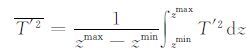
|
(4) |
就可得到温度扰动方差T′2.对各个剖面进行上述处理,然后对某个纬度范围或者某个区域的所有有效数据做平均可得到温度扰动方差月平均的剖面.
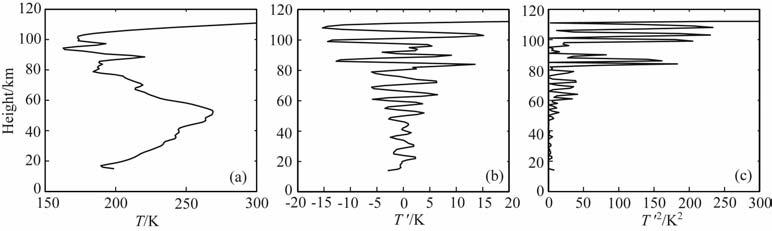
图 1a是2009年第1天在Lat=1.56°S,Lon=53.85°W 温度T(z)随高度的剖面.按照上述方法,进行滤波处理后,提取得到T′(z),如图 1b所示.图 1c是进一步计算得到的方差值随高度的分布,可以反映该时刻重力波随高度的变化情况.
|
图 1 2009年第1天某地区(Lat=1.56°S,Lon=53.85°W)的温度剖面及处理后的结果 Fig. 1 The temperature profile and corresponding results at (Lat=1.56°S,Lon=53.85°W) on the 1st day in 2009 |
Allen和Vincent[20]曾发现在低平流层(17~24km),重力波活动存在年变化,即在低纬地区的雨季(12~2月)和南半球中纬的冬季(6~8月)出现最大值.图 2 是以北京地区为例,给出了2002~2009年不同季节的扰动平均值(取对数)随高度的分布.从图中也可以看到冬季、夏季扰动明显强于春、秋季节;而冬季和夏季相比,在70km 以下的高度夏季弱于冬季,在70km 以上夏季变得比冬季要强.这一结果,与以前的相关研究结论相似[21, 22].重力波在其他位置的季节变化与北京上空非常类似,都有冬季和夏季显著增强的特征.因此,在下面的讨论中,主要考虑1月(冬季)和7月(夏季)的情况.

|
图 2 北京地区不同季节温度扰动的平均值 Fig. 2 Mean temperature perturbations of Beijingin different seasons |
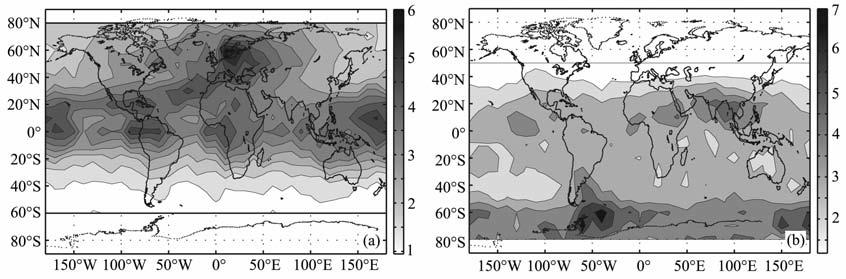
图 3是2009年1月和7月平流层全球重力波在37km 高度的分布图.由图 3a可见,重力波在25°N到25°S的低纬度扰动最大,这与热带对流有关.以北半球为例从图 3a中可以发现在中高纬度地区,较低平流层的重力波扰动在冬季半球比较大,这与冬季半球较强的行星波扰动对大气背景的改变有关[23, 24],大气背景的改变有利于重力波的垂直传播.尽管测量仪器和采样率不同,但是本文得到的多年平均分布特征与Wu等[6]使用2005年Aura卫星观测分析的结果一致.
|
图 3 37km 高度2009年(a)1月和(b)7月全球重力波分布图 Fig. 3 Global distribution of gravity waves in January (a), July (b) 2009 at 37 km |
比较图 3a和图 3b发现,在两半球的中高纬地区,7月的40°S~70°S的扰动值大于1月的40°N~70°N 的值.相反,南半球1 月的值小于北半球7 月的值.可见,平流层重力波的纬度分布不仅决定于季节,还依赖于不同的半球.
在下面的讨论中,我们将把8年数据按照月份进行平均,这样做的目的是为了得到重力波随季节的整体变化特征,暂时忽略重力波的逐年变化或更长周期的变化.图 4 为温度方差7 月份平均值在20km、40km 高度的赤道区分布图.由图中的比较可以看到,赤道峰值随着高度的增长而向北移动,可能是因为季节对流出现在热带区的夏季面.在更高的高度,亚热带峰值继续向北移动,类似于亚热带核随高度的增长而向北移动[12].

|
图 4 7月不同高度的重力波赤道区分布 (a)20km 高度;(b)40km 高度. Fig. 4 Global distribution of gravity waves in July at different altitudes (a)20 km; (b)40 km. |
另外,图 5为温度方差7月份平均值在南半球高纬度区分布图,南半球的扰动较大值位于高纬极区涡流的边缘,向北逐渐减弱.

|
图 5 7月份重力波在高纬区分布图 Fig. 5 Distribution of gravity waves in July at high latitudes |
Alexander等[3]认为重力波的纬度分布主要由行进重力波同背景风场的相互作用决定,同时也受到大气稳定性的影响.
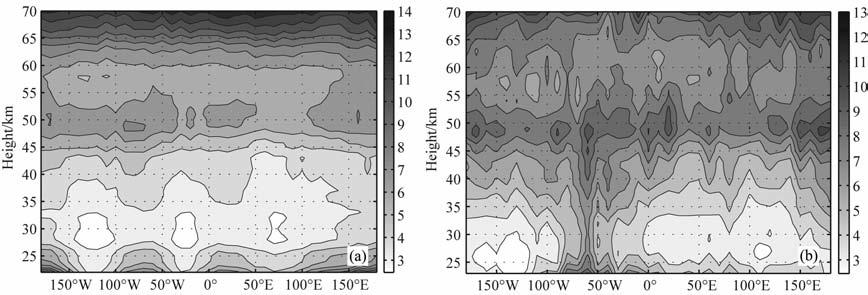
3.3 重力波随经度的变化图 6为温度方差1 月赤道区、7 月南半球高纬区平均值在不同高度的分布图.由图 6a可见,在冬季平流层极低处重力波扰动较大,而且其分布沿纬度圈方向有明显的变化.而对于更高的高度,这种随经度的变化而变化的分布趋势不太明显.对于向上传播的重力波,行星波结构在不同的区域起到了滤波的作用,从而也导致了重力波的经向调制.因此,Tsuda和Nishida[9]认为不同经度的重力波差异,可能是受行星波调制的作用.尽管重力波的时间、空间尺度都比行星波小,但是大尺度的行星波可看作背景的一部分,即纬度圈的平均风场和行星波的风场之和作为背景场,从而对重力波的经向活动性进行调制.另一方面,这种经度分布的差异,也体现了重力波波源的不均匀性,将在下面3.5节进一步讨论.
|
图 6 (a)1月份赤道区和(b)7月份高纬区经度-高度分布图 Fig. 6 Height-longitude cross-section of the gravity waves in January atequatorial region (a) and high latitudes (b) respectively |
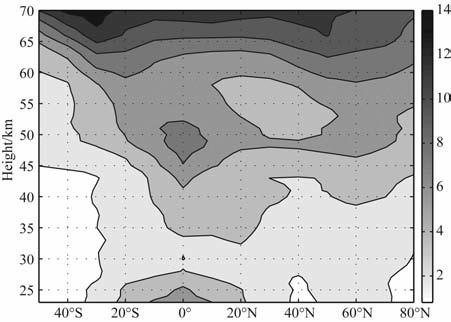
图 7是把2002~2009年1月平均扰动值沿着纬度圈做平均,得到温度方差的纬度-高度分布图.可见,重力波在15~45km 高度范围内是随纬度显著变化的.尽管20~40km 高度范围内扰动较大值集中于赤道附近,但是随着高度的上升较大值逐渐地分布在中纬地区.而且重力波扰动强度在低纬度随高度增长而变化的分布趋势为:在平流层下部随高度增长逐渐增大,但是在25~30km 处呈现下降趋势;超过33km 后直到42km 以下扰动大小基本不变,而后又随着高度的增长而增长.在陈泽宇和吕达仁[25]的传播性行星波的研究中也发现了这一特殊现象.
|
图 7 1月重力波全球纬度-高度分布图 Fig. 7 Height-latitude cross-section ofthe global gravity waves in January |
为了估计地形的影响,图 8 分析了温度方差1月份平均值在26~30km 高度赤道区和中纬区的分布.由图 8a可见,极大值集中分布于赤道两侧,并伴随着显著的随经度的变化,与前面的结果吻合.图中几个极大值的区域分别为南美洲、非洲和太平洋,这一特征可能与具体地形相关.
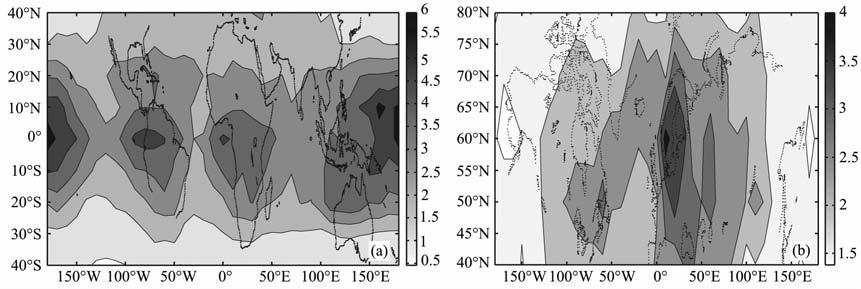
|
图 8 1月份26~30km(a)赤道区和(b)中纬区重力波分布图 Fig. 8 Global distribution of gravity waves in January at 26~30kmat equatorial region (a) and middle latitudes (b) |
在30°N~60°N 的纬度范围区域,如图 8b,扰动随着经度的改变而变化,发现跨大陆地区(亚欧大陆、北美)的大小要超过太平洋地区,即体现了重力波分布的陆海差异.而且进一步分析发现,较强扰动分布与地形密切相关,对应于美国东海岸、斯堪地内亚半岛和阿尔卑斯山脉(与AuraMLS[12]有相似的特征).以上较强的扰动归因于由地表风与地形的相互作用引起的山脉背风波动的作用.但是,重力波可以从源头传播很远的水平距离,地形对其分布的影响可能不会直接反映到平流层重力波的模式上.而且,重力波和背景风的作用以及风场的稳定性都会影响重力波垂直传播的特性,因此重力波模式在很大程度上会发生改变.
图 9分析了温度方差1月份平均值在50~55km高度赤道区和中纬区的分布.与图 8a比较,可以看到随着高度的增长赤道区扰动较大值分布向南半球移动.在图 9b中,扰动随着经度的改变以及陆海差异都不明显.因此,在这个高度,重力波分布与地形没有密切的关系.这说明重力波向上传播过程中受风场等因素的影响,分布特征发生了改变,重力波强弱与地形相吻合的特征逐渐消失.这也再次证明仅在较低高度的重力波分布与地形有密切关系.
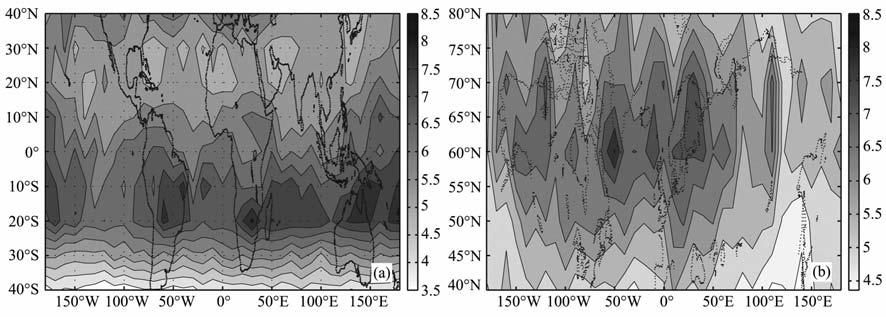
|
图 9 1月份50~55km(a)赤道区和(b)中纬区重力波分布图 Fig. 9 Global distribution of gravity waves in January at 50~55kmat equatorial region (a) and middle latitudes (b) |
使用8年TIMED 卫星上SABER 观测的温度剖面,我们得到了温度方差随季节平均变化的图像,结果表明,重力波在冬季和夏季明显较强.以重力波分布图扰动较为明显的1月(冬季)和7月(夏季)作为研究的重点,得到中层大气重力波的分布特征:
(1) 在25°N 到25°S的低纬度温度扰动最大;在中高纬度地区,扰动值在冬季半球比较大.而且,两半球的中高纬地区的比较,说明平流层重力波的纬度分布不仅决定于季节,还依赖于不同的半球.另外,在7月份赤道变化峰值随着高度增长向北移动,类似于亚热带核的移动趋势.南半球的扰动较大值位于高纬极区涡流的边缘,向北逐渐减弱.
(2) 对不同高度的重力波全球分布研究看到,在冬季较低的平流层,重力波扰动较大,而且有明显的沿纬度圈方向变化.而对于更高的高度,这种差异逐渐减弱.
(3) 由1月(冬季)重力波的纬度-高度图可见,重力波在15~45km 高度范围内是随纬度的变化而变化的.尽管20~40km 高度较大值集中于赤道附近,但是随着高度的上升较大值逐渐地分布在中纬地区.而且,重力波扰动强度随高度变化,在25~30km处呈现下降趋势,而超过42km 后又逐渐递增.
(4) 在1月(冬季)扰动分布中,赤道区极大值的区域分别为南美洲、非洲和太平洋,与具体地形相关.随着高度增加,波与地形相关性减弱.在30°N~60°N 的纬度范围区域,跨大陆地区(亚欧大陆、北美)的变化值要超过太平洋地区.这些陆海差异,归因于由地表风与地形的相互作用引起的山脉背风波动的作用.
对于重力波的全球分布特征与各种影响因素之间的关系,以及它的长期分布特征如QBO(准两年震荡)等,仍然需要进一步的研究.
| [1] | 易帆. 中高层大气重力波的研究——辨明近地空间环境扰动的关键过程. 中国科学基金 , 1997(3): 195–200. Yi F. Gravity waves in the middle and upper atmospheres. Bulletin of National Natural Science Foundation of China (in Chinese) , 1997(3): 195-200. |
| [2] | Olbers D J. Model of the oceanic internal wave field. Rev. Geophys , 1983, 21(7): 1567-1606. DOI:10.1029/RG021i007p01567 |
| [3] | Fritts D C, Alexander M J. Gravity wave dynamics and effects in the middle atmosphere. Rev. Geophys , 2003, 41(1): 1003. DOI:10.1029/2001RG000106 |
| [4] | Hirota I, Niki T. A statistical study of inertia-gravity wave in the middle atmosphere. J. Meteorol. Soc. Jpn , 1985, 63: 1055-1066. |
| [5] | Fetzer E J, Gille J C. Gravity wave variances in LIMS temperatures. Part I: variability and comparison with background winds. J. Atmos. Sci , 1994, 51(17): 2461-2483. DOI:10.1175/1520-0469(1994)051<2461:GWVILT>2.0.CO;2 |
| [6] | Wu D L, Waters J W. Satellite observations of atmospheric variances: A possible indication of gravity waves. Geophys. Res. Lett , 1996, 23(24): 3631-3634. DOI:10.1029/96GL02907 |
| [7] | Eckermann S D. On the observed morphology of gravity wave and equatorial-wave variance in the stratosphere. J. Atmos. Terr. Phys , 1995, 57(2): 105-134. DOI:10.1016/0021-9169(93)E0027-7 |
| [8] | Alexander M J, Tsuda T, Vincent R A. Latitudinal variations observed in gravity waves with short vertical wavelengths. J. Atmos. Sci , 2002, 59: 1394-1404. DOI:10.1175/1520-0469(2002)059<1394:LVOIGW>2.0.CO;2 |
| [9] | Tsuda T, Nishida M, Rocken C, et al. A global morphology of gravity wave activity in the stratosphere revealed by the GPS occultation data (GPS/MET). J. Geophys. Res , 2000, 105(D6): 7257-7274. DOI:10.1029/1999JD901005 |
| [10] | de la Torre A, Schmidt T, Wickert J. A global analysis of wave potential energy in the lower stratosphere derived from 5 years of GPS radio occultation data with CHAMP. Geophys. Res. Lett , 2006, 33: L24809. DOI:10.1029/2006GL027696 |
| [11] | Ratnam M V, Tetzlaff G, Jacobi C. Global and seasonal variations of stratospheric gravity wave activity deduced from the CHAMP/GPS satellite. J. Atmos. Sci , 2004, 61: 1610-1620. DOI:10.1175/1520-0469(2004)061<1610:GASVOS>2.0.CO;2 |
| [12] | Wu D L, Eckermann S D. Global gravity wave variances from Aura MLS: Characteristics and interpretation. J. Atmos. Sci , 2008, 65(12): 3695-3718. DOI:10.1175/2008JAS2489.1 |
| [13] | Xiao C Y, Hu X. Analysis on the global morphology of stratospheric gravity wave activity deduced from the COSMIC GPS occultation profiles. GPS Solut , 2010, 14(1): 65-74. DOI:10.1007/s10291-009-0146-z |
| [14] | Krebsbach M, Preusse P. Spectral analysis of gravity wave activity in SABER temperature data. Geophys. Res. Lett , 2007, 34: L0381. DOI:10.1029/2006GL028040 |
| [15] | van Zandt T E. A model for gravity wave spectra observed by Doppler sounding systems. Radio Sci , 1985, 20(6): 1323-1330. DOI:10.1029/RS020i006p01323 |
| [16] | 陈泽宇, 吕达仁. DE3潮汐的全球结构. 科学通报 , 2008, 53(23): 2940–2946. Chen Z Y, Lü D R. Global structure of DE3 tides. Chinese Science Bulletin (in Chinese) , 2008, 53(23): 2940-2946. |
| [17] | Siskind D E, Coy L, Espy P. Observations of stratospheric warmings and mesospheric coolings by the TIMED SABER instrument. Geophys. Res. Lett , 2005, 32(9): L09804. DOI:10.1029/2005GL022399 |
| [18] | Palo S E, Forbes J M, Zhang X, et al. Planetary wave coupling from the stratosphere to the thermosphere during the 2002 Southern Hemisphere pre-stratwarm period. Geophys. Res. Lett , 2005, 32: L23809. DOI:10.1029/2005GL024298 |
| [19] | Schroeder S, Preusse P, Ern M, et al. Gravity waves resolved in ECMWF and measured by SABER. Geophys. Res. Lett , 2009, 36: L10805. DOI:10.1029/2008GL037054 |
| [20] | Allen S J, Vincent R A. Gravity wave activity in the lower atmosphere: Seasonal and latitudinal variations. J. Geophys. Res , 1995, 100(D1): 1327-1350. DOI:10.1029/94JD02688 |
| [21] | 卞建春, 陈洪滨, 吕达仁. 用垂直高分辨率探空资料分析北京上空下平流层重力波的统计特性. 中国科学D辑(地球科学) , 2004, 34(8): 748–756. Bian J C, Chen H B, Lü D R. A statistical study of gravity waves from high vertical resolution sounding data at Beijing. Science in China Series D (Earth Sciences) (in Chinese) , 2004, 34(8): 748-756. |
| [22] | Rauthe M, Gerding M, Lübken F J. Seasonal changes in gravity wave activity measured by lidars at mid-latitudes. Atoms. Chem. Phys , 2008, 8: 6775-6787. DOI:10.5194/acp-8-6775-2008 |
| [23] | Fritts D C, Alexander M J. Gravity wave dynamics and effects in the middle atmosphere. Rev. Geophys , 2003, 41(1): 3-1. |
| [24] | 穆祥明, 马瑞平. 1980年中层大气温度波空间特征的初步分析. 空间科学学报 , 1997, 17(1): 76–84. Mu X M, Ma R P. Some features of planetary waves in the middle atmosphere in 1980. Chinese Journal of Space Science (in Chinese) , 1997, 17(1): 76-84. |
| [25] | 陈泽宇, 吕达仁. 利用卫星数据考察平流层传播性行星波活动特征. 地球科学进展 , 2009, 24(3): 320–330. Chen Z Y, Lü D R. Characteristics of the stratospheric travelling planetary waves revealed by using satellite data. Advances in Earth Science (in Chinese) , 2009, 24(3): 320-330. |
 2011, Vol. 54
2011, Vol. 54

