地球物理学报  2011, Vol. 54 Issue (6): 1672-1678   PDF    
引用本文
余先川, 代莎, 胡丹, 等. 基于Lasso函数的分层混合模糊-神经网络及其在遥感影像分类中的应用. 地球物理学报, 2011, 54(6): 1672-1678, doi: 10.3969/j.issn.0001-5733.2011.06.027.  
YU X C, DAI S, HU D, et al. HHFNN based on Lasso Function and its application in remote sensing image classification. Chinese J. Geophys. (in Chinese), 2011, 54(6): 1672-1678, doi: 10.3969/j.issn.0001-5733.2011.06.027.  
基于Lasso函数的分层混合模糊-神经网络及其在遥感影像分类中的应用
余先川1, 代莎1, 胡丹1, 江启煜2     
1. 北京师范大学信息科学与技术学院, 北京 100875;
2. 福建省闽东南地质大队, 泉州 362021
收稿日期 2010-05-24, 2011-05-30 收修定稿
基金项目: 国家高技术研究发展计划(863)(2007AA12Z156), 教育部新世纪优秀人才支持计划(NCET-06-0131), 国家自然科学基金(41072245), 北京市自然科学基金项目(4102029)资助.
摘要: 本文提出一种新的分层混合模糊-神经网络(HHFNN)算法.在模糊系统中使用Takagi-Sugeno模型和三角波隶属函数.同时, 为降低离散输入变量中可能存在的强交互作用, 采用了系数收缩机制中的Lasso函数.最后, 以福建的漳平洛阳-安溪潘田地区LANDSAT ETM+遥感影像数据地物分类为例, 应用本文的改进算法与其他神经网络算法进行分析比较, 得到了较高的分类精度, 验证了采用基于Lasso函数的T-S型分层混合模糊-神经网络的可行性和有效性, 可作为一种新的遥感影像地物分类方法.
关键词: Takagi-Sugeno模型      分层混合模糊-神经网络      Lasso函数      训练算法      遥感影像分类     
HHFNN based on Lasso Function and its application in remote sensing image classification
YU Xian-Chuan1, DAI Sha1, HU Dan1, JIANG Qi-Yu2     
1. College of Information Science and Technology, Beijing Normal University, Beijing 100875, China;
2. Southeast Fujian Geologic Party, Quanzhou 362021, China
Abstract: In this paper, a new algorithm for hierarchical hybrid fuzzy-neural network model is proposed. Takagi-Sugeno model and triangular membership function are adopted in fuzzy system, and lasso function of coefficient contraction method is used to reduce the strong interaction among discrete input variables. In the end, an experimental test on surface features classification by using LANDSAT ETM+ remote sensing image data of Zhangping Luoyang-Anxi Pantian in Fujian Province is conducted. Compared with other neural networks, the classification with the proposed approach is the most accurate, which proves its feasibility and validity, and can be used as a new surface features classification method on remote sensing image.
Key words: Takagi-Sugeno model      Hierarchical hybrid fuzzy-neural networks      Lasso function      Training algorithm      Remote sensing image classification     
1 引言

现代遥感技术的快速发展与新型传感器的不断涌现，使得利用遥感数据对地进行观测进入了一个新的多元的时代.从不同平台上获取的不同空间分辨率､不同时间分辨率以及不同光谱分辨率的遥感影像，形成了多级金字塔式的影像数据源.

如此大量的多种形式遥感影像，迫切需要能得到更广泛的利用.然而这些数据经常是高维的且同时含有离散和连续变量.在系统建模中，为了避免信息的流失，必须使用某种方法将两种变量统一到同一种类型，而不是简单地把一种类型当作另一种类型直接处理.常用的处理方法有两种:一是将连续变量离散化，如王飞等[1]通过遗传算法找到全局最优离散策略，张化光等[2]提出基于模糊粗糙集和断点简约化离散化方法等；二是将离散变量连续化，如车燕等[3]通过分段线性插值构造出与原离散变量具有相同期望和方差的连续变量，Wang等[4]提出分层混合模糊-神经网络(HHFNN)模型，用模糊子系统先将离散变量连续化，再将模糊子系统的中间输出与连续变量一起输入到神经网络进行处理，后来Feng等[5]又对此模型进行了改进，提出基于Gaussian隶属函数的分层混合模糊-神经网络模型.

然而，遥感影像数据的变量通常也不是相互独立的，在多个变量间可能会存在强交互作用，常用的去相关方法如主成分分析(PCA)[6]通过正交变换得到一组两两正交的向量，但丢弃了低方差向量，且主成分分析还未见文献说明适用于处理离散变量.对于自变量的多重共线性，主要通过变量筛选来解决.即在大量的因变量中确定一个较小的变量子集，使得每个变量和目标变量有较强的关系.典型的做法包括Stepwise.FSLR，子集选择等.

由于变量选择的过程是离散的，即变量要么保留在模型中，要么排除在模型以外，数据中很小的变化会导致模型的变量很不相同.其固有的不连续性导致模型不稳定，当变量个数很多时，由于需要搜索所有的子集，对于P个自变量来讲，全部可能的子集数目就有2P-1个之多.一般来说，当P个数大于30就没有办法进行计算了.岭回归是一个可以连续收缩系数的过程，因此更稳定，但是它不能设定每个系数为0，因此模型解释性会大打折扣.

1996年Tibshirani[7]提出了基于调整机制的模型Lasso.其主要优点在于同时可以进行连续的选择变量和模型参数估计.基于调整机制的模型在实践中发现明显比未使用调整机制的模型预测精度要高，而且还保持了其良好的解释性能.

本文使用了分层混合模糊-神经网络模型，在模糊子系统部分选用T-S模型，隶属度函数采用三角波隶属函数，在模糊推理规则部分选用Lasso函数，并根据这种模糊推理规则，使用梯度下降法给出了新的训练算法，训练的参数除了隶属度函数的中心和神经网络的权重值及偏置值以外，增加了Lasso函数的限制系数.最后用福建漳平洛阳-安溪潘田地区遥感影像数据进行分类实验，实验结果显示，与BP算法[8]､WangDi提出的HHFNN算法和FengShuang改进的HHFNN算法相比，基于Lasso函数的T-S型分层混合模糊-神经网络算法在分类精度上更有优势.

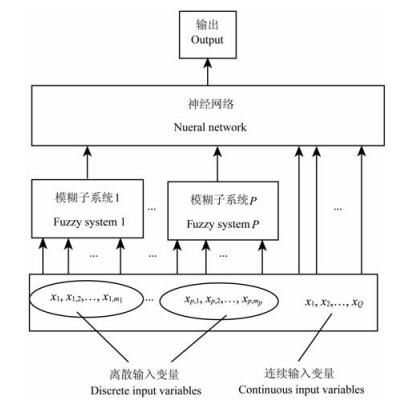
2 分层混合模糊-神经网络模型

分层混合模糊-神经网络模型由一个模糊系统和一个神经网络系统复合而成，其拓扑结构如图 1所示.

图 1 分层混合模糊神经网络的结构 Fig. 1 Structure of hierarchical hybrid fuzzy-neural networks

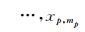
网络模型中一共有P个模糊子系统，第个模糊子系统的输入变量为:共mp个.在分层混合模糊神经网络模型中，模糊系统用于处理离散变量，并将其转换为连续变量，神经网络系统同时处理原始连续变量和由模糊系统生成的连续变量，很好地解决了离散和连续变量并存的问题.

3 基于Lasso函数的T-S型分层混合模糊-神经网络模型 3.1 模糊子系统部分

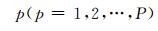
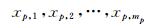
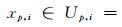
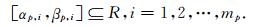
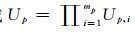
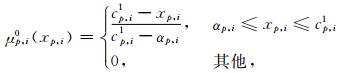
假设网络模型中一共有P个模糊子系统，第个模糊子系统的输入变量为:于是该模糊子系统的输入论域输出论域记为在每个输入变量xp, i的论域Up, i上进行等距模糊划分，设划分数为Np, i，从而每个论域Up, i上有Np, i+1个模糊集，其隶属度函数采用三角波函数.

设依次表示各三角波函数的中心，于是第p个模糊子系统的第i个输入xp, i的隶属度可由下列式子计算:

(1)

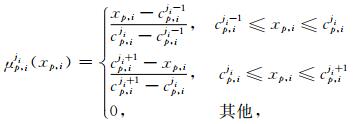
(2)

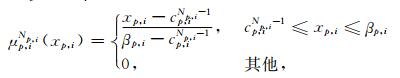
(3)

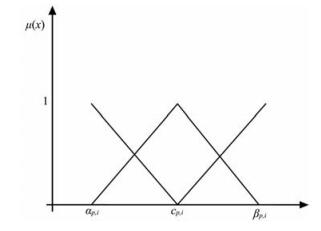
本文取Np, i=2，则xp, i论域的模糊集划分如图 2所示.

图 2 xp, i论域的模糊模糊集划分(Np, i=2) Fig. 2 Fuzzy set partition ofxp, i(Np, i=2)

对于第P个模糊子系统，采用Takagi-Sugeno模型来实现模糊推理过程.该模型的主要特点是:模糊规则的后件部分采用的是输入变量的函数(一般使用线性函数)，而在Mamdani模型中模糊规则后件采用的是普通的模糊集.研究发现，Takagi-Sugeno型模糊系统能够充分利用输入变量的特征，使用的模糊规则数通常少于Mamdani型模糊系统，同时具有较为简单的模糊化过程，因此它也被广泛地用于复杂或非线性系统的建模[9-11].

推理规则表示为如下形式:

在Takagi-Sugeno模型中，推理后件中的函数f(·)选择系数收缩方法中的Lasso函数[12].

Lasso (The Least Absolute Shrinkage and Selection Operator, Tibshirani (1996))方法是一种收缩估计.它通过构造一个L1罚函数得到一个较为精炼的模型，区别于岭回归使用的k罚，使得它收缩一些系数，同时设定另一些系数为0.因此保留了子集收缩和岭回归的优点.它和岭回归一样，也是一种处理具有复共线性数据的有偏估计.

Lasso方法采用如下函数形式:

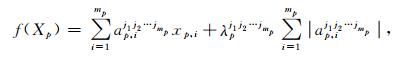
(4)

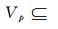
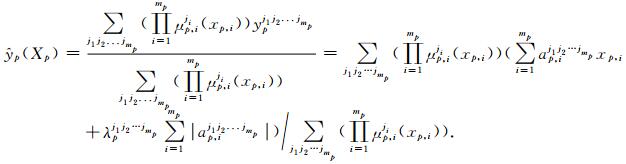
其中是输入变量xp, i的系数，是模型中约束系数，模糊子系统的输出为

(5)

3.2 神经网络部分

在上层的神经网络中，采用三层前向网络，输入层神经元个数为(P+Q)个(P表示模糊子系统的个数，Q表示输入中连续变量的个数)，中间隐层神经元个数为H，输出层只有一个神经元.输入层到隐层的权重矩阵分为两部分，其中连接模糊子系统输出与隐层神经元的权重用矩阵Wp=(Wjp)H×P表示，连接连续输入变量与隐层神经元的权重用矩阵WQ=(Wjp)H×P表示，隐层神经元偏置值向量记为b=(bj)1×H，隐层到输出层权重记为向量g=(gj)1×H，其偏置值记为d，网络输出记为o.隐层神经元的传递函数采用Sigmoid函数f1(x)=1/(1+e-x)，输出层神经元采用线性传递函f2(x)=x，则输出可写为[13~16]

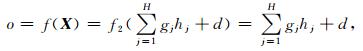
(6)

其中，X=(X1，X2，…，XP，XQ)为整个网络的输入向量，hj为隐层中第j个神经元的输出，则其计算公式为

(7)

故输出可写为

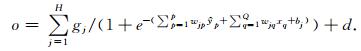
(8)

4 训练算法

在上层神经网络的训练中使用梯度下降法.目标误差函数使用

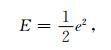
(9)

其中e=t-o，t是实际目标输出值，那么

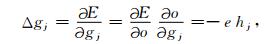
(9)

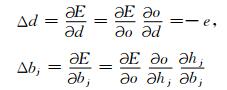
(9)

(9)

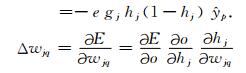
(9)

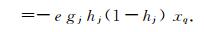
(9)

于是由(10)~(14)式得到上层神经网络的各个参数的更新公式:

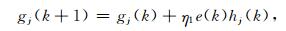
(15)

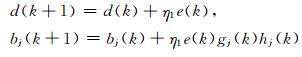
(16)

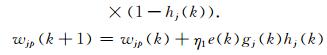
(17)

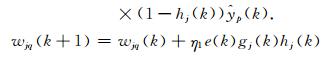
(18)

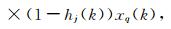
(19)

其中j=1，2，…，H，p=1，2，…，P，q=1，2，…，Q，η1是学习速度.

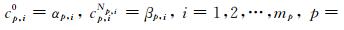
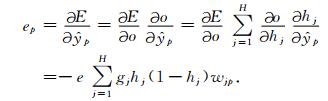
模糊系统的参数更新.对于第p(p=1，2，…，P)个模糊子系统，我们要在迭代中调整的参数为首先算从上层神经网络反向传递到第p个模糊子系统的误差为

(20)

于是采用如下方法更新隶属函数中心参数:

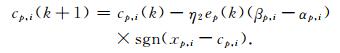
(21)

对于Lasso函数，由于

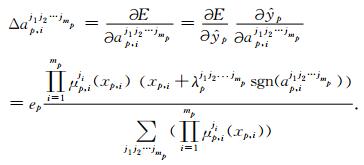
(22)

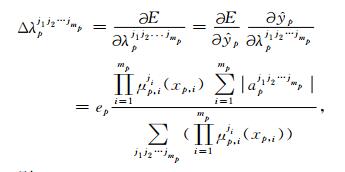
(23)

则

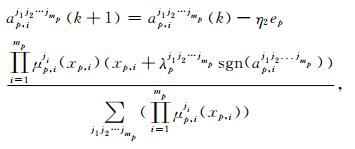
(24)

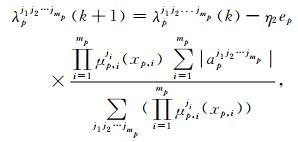
(25)

其中i=1，2，…，mp，p=1，2，…，P，η2是学习速度.

完整的训练算法如下:

步骤1 (i)把输入变量分为连续和离散变量两部分，然后将离散变量分为P组，将第p组离散变量作为第p个模糊子系统的输入.如果问题中的几个离散变量之间存在明显的关系，那么就可以把相互之间有联系的离散变量分为一组，否则采取随机的方法将离散变量进行分组.为了避免模糊系统中出现的“维数灾难"问题和实现比较好的学习效果，每个模糊子系统的输入的离散变量个数不要超过4个.

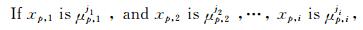
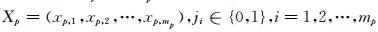
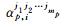
(ii)对训练数据进行归一化处理.设训练数据组为(X，T)，其中输入数据对应输出数据n为训练样本数，m为输入变量个数，用以下公式将他们归一到[0，1]，并记为(X，T)，(iii)确定离散输入变量xp, i的论域U并在论域上取两个模糊集，每个模糊集的隶属函数由(1)~(3)定义.

步骤2 网络参数初始化，用(-1，1)上的随机数初始化上层神经网络的各个权重WP，WQ，c和各层偏置值b，d；下层模糊子系统中参数初始值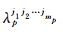P设定目标训练误差限ε和最大训练回合数K.

步骤3 开始训练网络.训练回合数k=1，样本编号r=1，将训练集中的第一个学习样本输入到网络中.

步骤4 在第k个训练回合中，对于第r个学习样本(Xr，Tr)(Xr=(xrj)r×m))，计算网络输出or，误差er=tr-or，根据(15)~(19)､(21)和(24)~(25)更新网络参数Wjp，Wjq，cj，bj，d和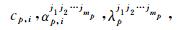

步骤5 若r＜n，则r=r+1并转步骤4.

步骤6 计算第k个训练回合中网络的均方误差值若MSE＜ε或者k达到最大训练回合数K，则训练结束，否则k=k+1并转步骤4.

5 实验结果与分析

实验数据选用福建漳平洛阳-安溪潘田地区LANDSATETM+影像(图 3)，时相为2000年5月11日.实验目的是为了测试网络的分类精度以及前述算法对遥感影像地物分类的有效性，检验网络的泛化能力.

图 3 福建漳平洛阳-安溪潘田地区遥感影像 Fig. 3 color image of Zhangping and Anxi, Fujian Province

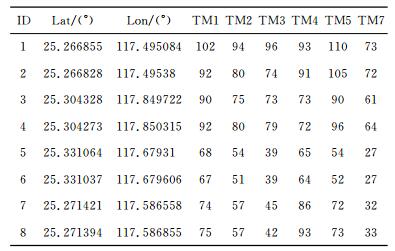
在实验中用到其中TM1､TM2､TM3､TM4､TM5､TM7共6个波段，空间分辨率均为30 m.图像质量良好，无云影，较清楚地反映了该地区土地覆盖情况.通过对实际情况的目视判读，本处将影像中的地物分为裸露地区､植被､河流和阴影四类[17].实验中以一个像素点为一个样本，使用ENVI4.6在影像上截取样本集数据，共获取681样本，其中供网络学习的训练样本481个，同时为了检查网络的泛化能力，每个类别准备了50个测试样本，共200个测试样本.图 4为样本集图像，表 1为部分样本集数据，数据包含了样本点的经纬度和6个波段的像素值.

表 1 部分样本集数据 Table 1 Part of sample data
图 4 样本集数据 Fig. 4 Data of sample

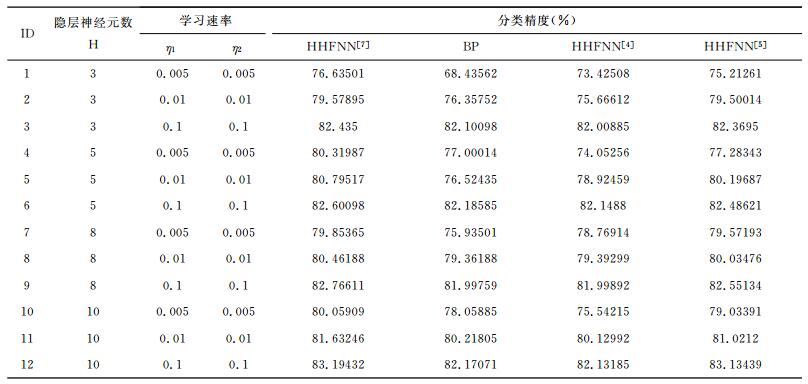
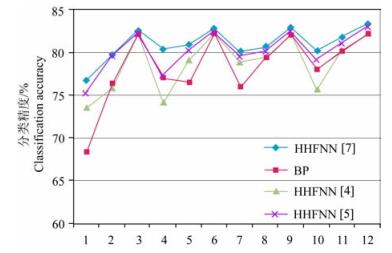
选取影像数据的6个波段像素值，作为网络的6个输入变量.由于遥感数据属性有限，实验采取随机选取其中的4个波段数据当作离散变量，剩余的2个波段当作连续变量.因此，本文采取2个模糊子系统分别处理2组离散变量(随机分组)，即P=2，连续变量个数Q=2.分别在不同的隐层神经元数和学习速率下，比较基于Lasso函数的HHFNN算法､BP算法､Wang等提出的HHFNN算法和Feng等提出的HHFNN算法的分类精度(结果见表 2和图 5).

表 2 各神经网络算法的分类精度 Table 2 Classification accuracy of neural network algorithms
图 5 各神经网络分类精度对比 Fig. 5 Comparison of the classification accuracy of neural network

从表 2和图 5中可以看到，分类精度方面，在相同隐层神经元个数和训练回合数的条件下，本文提出的算法所得到的分类精度都要高于BP算法､Wang等提出的HHFNN算法和Feng等改进的基于Mamdani模型的HHFNN算法的分类精度.这是因为在模糊子系统中，Lasso函数能有效地去除变量间的交互性，使输入到神经网络系统的变量变得连续且独立，从而提高了整个系统的精度.实验证明，基于Lasso函数的T-S型分层混合模糊-神经网络适用于遥感影像数据分类识别.

6 结论

在遥感影像处理中，为解决变量间存在强交互作用的问题，本文改进了Wang等提出的分层混合-模糊神经网络模型，模糊子系统选用了T-S模型､隶属度函数使用三角波隶属函数，在模糊推理规则部分使用了系数收缩机制中的Lasso函数.使用梯度下降法详细推导了各个参数的迭代规则，并给出了完整的训练算法.最后用福建漳平洛阳-安溪潘田地区遥感影像数据进行了分类实验，实验结果显示，在训练回合数､隐层神经元个数和学习速度相同的情况下，得到的分类精度要优于BP算法､Wang等提出的HHFNN算法和Feng等改进的基于Mamdani模型的HHFNN算法.

本文还可以在很多方面继续深入研究:文中在训练过程中采用梯度下降法调整参数，实际上可以使用其他方法，如最小二乘法；还可以探讨主成分分析是否适用于处理离散变量，以便进一步提高模型的精度.

致谢

国土资源部航遥中心的晋佩东研究员､北师大贺辉博士对本文的研究工作也做出了贡献，北师大空间多源信息融合与分析校级重点实验室提供了优越的研究环境，在此致以衷心的感谢.感谢评审专家为本文提出诚挚宝贵的意见.

参考文献
[1] 王飞, 刘大有, 薛万欣. 基于遗传算法的Bayesian网中连续变量离散化的研究. 计算机学报, 2002, 8(25): 794–800. Wang F, Liu D Y, Xue W X. Discretizaing continuous variables of bayesian networks based on genetic algorithms. Chinese Journal of Computers (in Chinese) (in Chinese), 2002, 8(25): 794-800.
[2] 张化光, 徐悦, 张秋野. 基于模糊粗糙集的系统连续变量离散化方法. 东北大学学报, 2008, 1(29): 1–4. Zhang H G, Xu Y, Zhang Q Y. On the discretization algorithm based on fuzzy rough set for continuous system variables. Journal of Northeastern University (in Chinese) (in Chinese), 2008, 1(29): 1-4.
[3] 车燕, 任开隆, 王信峰. 离散型随机变量连续化处理方法. 北京联合大学学报, 2001, 15(3): 65–68. Che Y, Ren K L, Wang X F. The method of how to continue the disperse stochastic variable. Journal of Beijing Union University (in Chinese) (in Chinese), 2001, 15(3): 65-68.
[4] Wang D, Zeng X J, John A K. Hierarchical hybrid fuzzy-neural networks for approximation with mixed input variables. Neurocomputing, 2007(70): 3019-3033.
[5] Feng S, Li H X, Hu D. A new training algorithm for HHFNN based on Gaussian membership function for approximation. Neurocomputing, 2009(72): 1631-1638.
[6] Turk M, Pentiand A. Eigenfaces for recognition. Journal of Cognitive Neuroscience, 1991, 1(3): 71-86.
[7] Tibshirani R. Regression shrinkage and selection via the Lasso. J. Roy. Statist. Soc. Ser, 1996, 58(1): 267-288.
[8] Stoeva S, Nikov A. A fuzzy backpropagation algorithm. Fuzzy Sets Syst, 2000(112): 27-39.
[9] Zadeh L A. Fuzzy sets. Information and Control, 1965(8): 338-353.
[10] Buckley J J, Hayashi Y. Fuzzy neural networks: a survey. Fuzzy Sets Syst, 1994(66): 1-13.
[11] Takagi T, Sugeno M. Fuzzy identification of systems and its application to modeling and control. IEEE Trans.Systems Man Cybernet., 1985(15): 116-132.
[12] Trevor H, Robert T.统计学习基础:数据挖掘、推理与预测.范明等译, 北京:电子工业出版社, 2004 Trevor H, Robert T. The elements of statistical learning: data mining, inference, and prediction. Springer, 2003.
[13] 余先川, 曹婷婷, 杨春萍, 等. 基于稀疏成分分析的遥感影像分类. 地球物理学进展, 2009, 24(6): 2274–2279. Yu X C, Cao T T, Yang C P, et al. Remote sensing image classification based on sparse component analysis. Progress in Geophysics (in Chinese) (in Chinese), 2009, 24(6): 2274-2279.
[14] 余先川, 初晓凤, 曹恒智, 等. 基于拉格朗日分解算法的SAR图像混合像元分解. 地球物理学进展, 2010, 25(1): 316–323. Yu X C, Chu X F, Cao H Z, et al. Decomposition of SAR image mixed pixels based on lagrangian constrained neural network. Progress in Geophysics (in Chinese) (in Chinese), 2010, 25(1): 316-323.
[15] 唐秋华, 刘保华, 陈永奇, 等. 结合遗传算法的LVQ神经网络在声学底质分类中的应用. 地球物理学报, 2007, 50(1): 313–319. Tang Q H, Liu B H, Chen Y Q, et al. Application of LVQ neural network combined with the genetic algorithm in acoustic seafloor classification. Chinese J. Geophys.(in Chinese) (in Chinese), 2007, 50(1): 313-319.
[16] 赵海娟, 王家龙, 宗位国, 等. 用径向基函数神经网络方法预报太阳黑子数平滑月均值. 地球物理学报, 2008, 51(1): 31–35. Zhao H J, Wang J L, Zong W G, et al. Prediction of the smoothed monthly mean sunspot numbers by means of radial basis function neural networks. Chinese J. Geophys. (in Chinese) (in Chinese), 2008, 51(1): 31-35.
[17] 吴媚, 符力耘, 李维新. 高分辨率非线性储层物性参数反演方法和应用. 地球物理学报, 2008, 51(2): 546–557. Wu M, Fu L Y, Li W X. A high-resolution nonlinear inversion method of reservoir parameters and its application to oil/gas exploration. Chinese J. Geophys.(in Chinese) (in Chinese), 2008, 51(2): 546-557.