2. 中国地质大学(北京)地球物理与信息技术学院, 北京 100083
2. School of Geophysics and Information Technology, China University of Geosciences(Beijing), Beijing 100083,China
大地电磁法三维正、反演问题是国际和国内地球物理学家研究的热点和难点问题.正演是反演的基础,如何实现快速、高精度、适用性强的正演已成为反演算法能否取得成功的关键[1, 2].当前,许多地球物理工作者致力于大地电磁三维正反演问题的研究.采用的数值计算方法主要有基于积分方程的积分方程法、边界单元法和基于微分方程的有限差分法、有限元方法,随着计算机技术的发展和新的算法技术的引进,近十年大地电磁三维正反演取得了丰硕的成果[3-9].在有限差分法方面,最早Jones(1972年)[10]和Lines(1973 年)[11]提出三维有限差分法,采用高斯-塞德(Gauss-Seidel)松弛技术求解简单模型三维网格化电场的双旋度扩散方程.随后Smith(1991年)[12]和Mackie(1993 年)[13]对有限差分方法进行改进,提出了三维交错采样有限差分方法,并采用双共轭梯度稳定算法(BICGSTAB)求解离散的线性方程组.该方法克服传统有限差分法造成磁场切分量不连续的特点,正演计算变得快速、精确、适用性强.在这之后许多地球物理工作者围绕着交错采样有限差分算法展开研究,并且取得一系列成果[14-19].在国内,谭捍东等(2003年)[20]系统地论述了从磁场出发的大地电磁三维交错采样有限差分法数值模拟算法实现过程,且在2006年成功地将该算法移植到并行机上运行,从而大大提高了三维正演的计算速度[21].沈金松等(2003 年)[22]则从电场出发实现了大地电磁三维交错采样有限差分正演.在这些研究中,如何快速、准确地求解离散线性方程组成为关键,其中沈金松[22]、Mackie[13]等在求解线性方程组时提出了散度校正方法,指出根据Maxwell方程可知电场或磁场散度为零,在正演中强制校正使得每个节点的磁场(电磁)散度为零,从而提高求解结果的精确度.但他们的研究未涉及如何进行散度校正以及散度校正对正演结果、计算时间和收敛速度等的影响.
本文在对Mackie等[13]、谭捍东等[20, 21]提出的从磁场出发的大地电磁三维交错采样有限差分数值模拟算法的基础上,对Maxwell方程中磁场散度为零的方程进行分析,提出了三种磁场散度校正方法.对不采用散度校正和采用三种不同方法散度校正的四种方案的大地电磁三维正演的求解速度、迭代精度、迭代次数及其误差衰减规律进行分析,提出了一种适合大地电磁三维正演的有效、快速的散度校正方法.
2 大地电磁三维交错采用有限差分数值模拟 2.1 求解区域交错采样离散化对求解区域在直角坐标系下采用一系列平行于X、Y、Z坐标轴的三组平面进行剖分.设剖分段数分别为NX、NY、NZ,将产生NX×NY×NZ个六面体剖分单元.对其任意一个六面体剖分单元(如图 1a)定义电场分量在六面体的12条边上,磁场分量在垂直六面体的六个面中心上,称该单元为电场单元.然而对于互相相邻的八个六面体单元格中心点连成六面体,可以看出磁场分量在垂直六面体的六个面中心上,电场分量在六面体的12 条边上,与磁场单元刚好相反,称为电场单元.且电场单元和磁场单元相互交错.

|
图 1 交错网格单元 (a)磁场单元采样示意图;(b)电场单元采样示意图. Fig. 1 The cell of stragered-grid (a)The sample method of magnetic field cell;(b)The sample method of electric field cell. |
上面的这种电磁场分量的定义称为交错采样,相对于传统的电磁场定义方法的主要优势为:一方面满足电磁场双旋度方程中旋度运算的右手螺旋定律,另一方面可以避免磁场切分量由于普通有限差分方式造成的磁场切分量不连续现象.且交错采样最大特点是能自动保证电磁场分布遵守能量守恒定律,在求得电(或磁)场的分布后,可以方便地求得磁(或电)场的分布.
2.2 Maxwell 方程及其离散化由大地电磁法理论可知,在准静态条件下频率域内的Maxwell方程组积分形式为:

|
(1) |
对于方程组(1)的第一式:等式左边为环路积分,右边为曲面积分.根据图 1a所示,采用有限差分进行离散化可得:
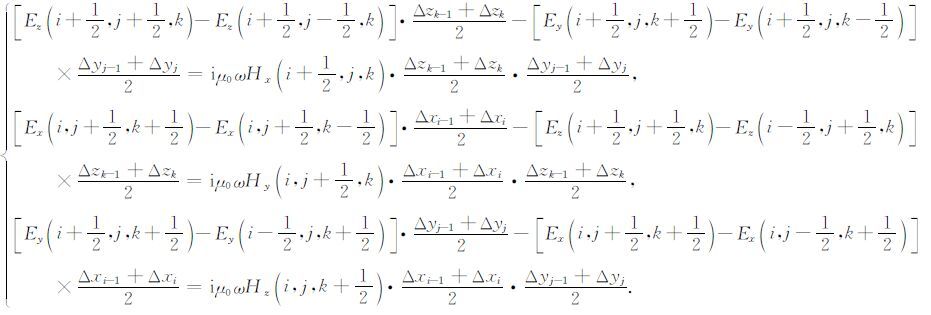
|
(2) |
同理,根据图 1a和方程组(1)中第二式可得另外一组离散的方程组为:

|
(3) |
其中σx,σy,σz分别为X,Y,Z方向的电导率.它们的表达式分别为:

|
(4) |
根据方程组(2)中第2式和方程组(3)中的第1、3式,消去电场分量可以得到一组关于磁场Hy的离散方程组为:

|
(5) |
其中式中的各项系数为:
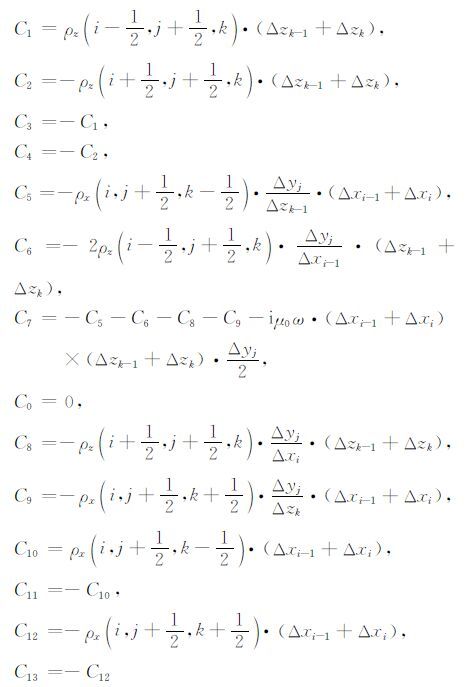
|
在求解区域内部的每一个Hy分量都可以产生一个线性方程式,共有(NX-1)×NY×(NZ-1)个方程,与待求分量个数相同.与此相同,可以推导出关于Hx,Hz分量的等式,这样就能合成关于求解磁场三分量的线性方程组,总数为(NX-1)×NY×(NZ-1)+ NX×(NY-1)×(NZ-1)+ (NX-1)×(NY-1)×NZ.
2.3 边界条件和线性方程组求解采用第一类边界条件,对求解区域外的上层增加若干空气层,空气中的顶边界设置大地电磁场源值.对于地下底边界,将边界以下区域看成由均匀半空间或层状介质组成,根据波阻抗Zxy和Zyx与磁场的关系可推出边界条件的表达式(详细见参考文献[20]).四个侧面磁场值可以采用二维MT 在不同模式下正演计算求得.
在方程组求解方面,采用当今地球物理正演中常用的预处理双共轭梯度稳定算法求解该大型、对称、稀疏、复离散线性方程组,且预处理方法为不完全LU 分解.该求解方法具有良好的稳定性和收敛性[23].
假设线性方程组为Ax=b,对系数矩阵A进行不完全LU 分解:
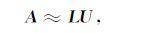
|
(6) |
其中L为下三角矩阵,U为上三角矩阵.
对系数矩阵分解完成后,线性方程组可改写为:

|
(7) |
其中M=LU.假设A′=M-1A,b′=M-1b,可以将以上线性方程组进一步改写为:

|
(8) |
令ri表示残差向量,pi表示搜寻方向,ri*为任意给定向量.取初值:

|
(9) |
不完全LU 分解双共轭梯度稳定算法求解线性方程组的迭代形式为:
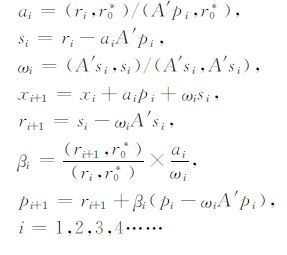
|
(10) |
通过对Maxwell方程组第一式和第二式采用有限差分和交错采样的方式进行离散得到一组关于磁场的线性方程组,然后采用不完全LU 分解预处理双共轭梯度稳定算法求解.在该三维数值模拟过程中由于计算机的截断误差、迭代求解的误差积累、模型电阻率突变、不等距剖分等因素的影响,不能保证每个求解单元内的磁场散度均为零.然而据Maxwell方程组(1)第三式可知,在每个求解单元内必须满足磁场散度为零(磁场是无源的)的条件,如果不满足上述条件会影响计算结果的准确性和精度.因此在电磁三维正演求解过程中采用磁场散度校正的方法对迭代求得的磁场值进行修正.本文从磁场散度为零等式出发,提出了三种磁场散度校正方法,分别为直接磁场散度校正(DDCM)、磁场散度残差复校正(RPCM)、磁场散度残差实校正(RRCM).
3.1 直接磁场散度校正(DDCM)首先考虑到Maxwell方程组微分形式关于磁场是无源的等式,即
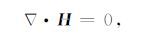
|
(11) |
将(11)式改写成笛卡尔直角坐标系三分量的形式为:
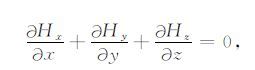
|
(12) |
采用有限差分对上式进行离散.
对网格单元中任意一点(i,j,k)按照图 2 进行离散得:
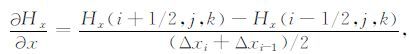
|
(13) |
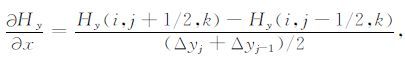
|
(14) |
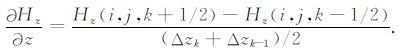
|
(15) |

|
图 2 直接磁场散度校正示意图 Fig. 2 The sketch of direct divergence correction of magnetic field |
将(13-15)式代入(12)式可以得到:
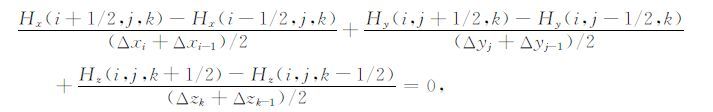
|
(16) |
对上式进行变形,可以得到关于磁场三个方向的校正公式:
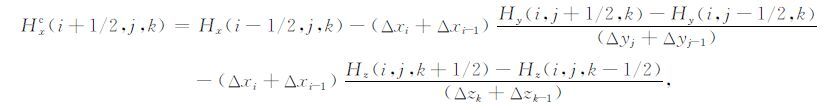
|
(17) |
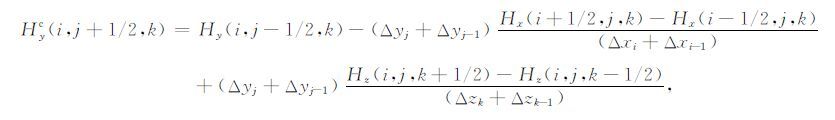
|
(18) |
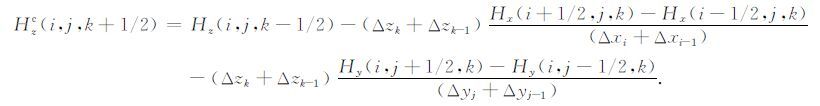
|
(19) |
前述的直接磁场散度校正方法(DDCM)由于不对称的存在,可能会造成线性方程组求解的不稳定.因此拟考虑构建一个对称的磁场散度校正方法.从(16)式可以看出每个磁场单元内磁场散度都应为零.但在实际的方程求解中,每个磁场单元都会有散度残差存在.据此,定义磁场的散度残差为:
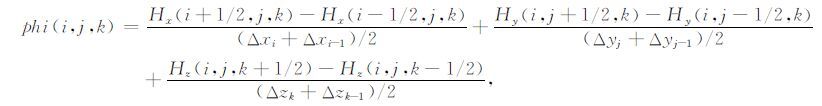
|
(20) |
选取一个磁场残差单元格,由任意一个节点和周围六个节点组成.考虑到磁场有三个分量,要对磁场进行校正必须定义三个方向的残差,采用有限体积的思想定义三个方向的残差分别为:
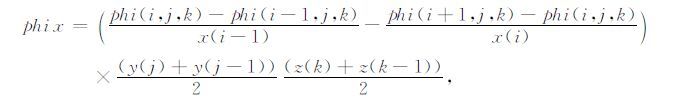
|
(21) |
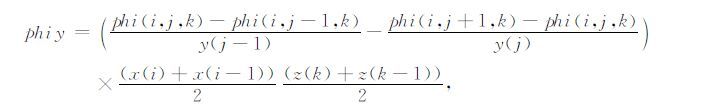
|
(22) |
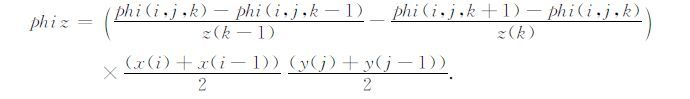
|
(23) |
在实际计算过程中不能保证一个单元内的残差为零,但可保证每个单元内三个方向的磁场散度残差之和为零.即:
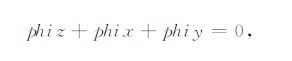
|
(24) |
将(21-23)式代入上式可得:
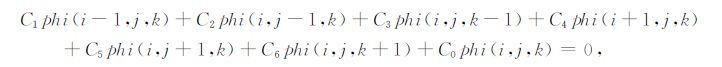
|
(25) |
其中:
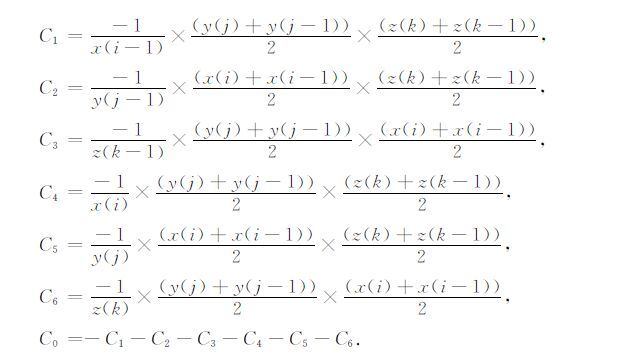
|
采用预处理共轭梯度算法求解上式,可以得到每个单元格的残差,然后利用磁场修正公式进行修正.磁场修正公式为:
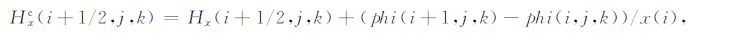
|
(26) |
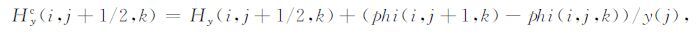
|
(27) |
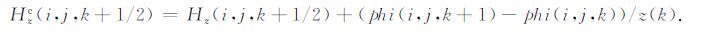
|
(28) |
在方程(25)中,其系数C0,C1,C2,C3,C4,C5,C6 都为实数.根据复数运算法则,可以将上述方程分解成两个实部和虚部的实数方程组进行求解.这样就能够减少一半的计算量,加快求解速度.其实部和虚部方程分别为:
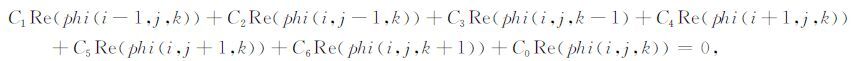
|
(29) |
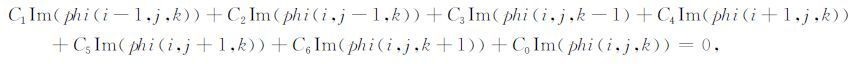
|
(30) |
式(29)和式(30)中的系数和式(25)中的相同,Re表示复数的实部,Im 表示复数的虚部.
同样,可以采用实数的预处理共轭梯度算法求解式(29)和(30),得到实部残差和虚部残差,然后对磁场进行修正.其修正公式为:
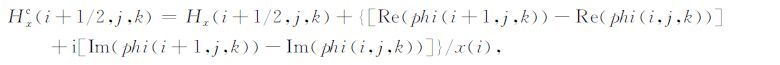
|
(31) |
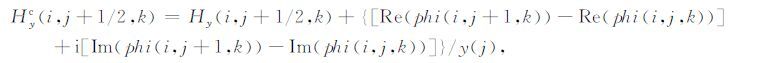
|
(32) |
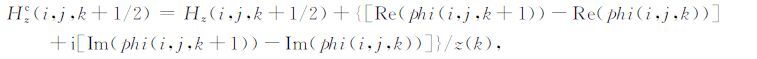
|
(33) |
为了验证四种散度校正方法(NDCM、DDCM、DPCM、DRCM)的可行性及计算效率、适用性、优劣性,本文设计了三个典型地电模型(垂直接触带、低阻异常模型和标准模型),从计算正演计算的速度、迭代次数、误差衰减曲线、计算时间、计算结果等方面进行分析.
本文所有算法均在Microsoft Visual Studio 2008开发平台上采用Inter visual fortran 11.1 编写.程序运行环境为Pentium D 3.0GHz处理器、4G内存、64位XP系统计算机.
4.1 垂直接触带模型垂直接触带模型如图 3a所示,地下均匀半空间中左半空间的电阻率为10Ωm、右半空间电阻率为1000Ωm.d′Erceville和Kunetz[24]讨论了垂直接触带模型TM 模式的解析计算公式,并给出了图 3a所示模型在频率为1Hz的解析解[20].为便于比较,本文采用三种散度校正(NDCM、RPCM、RRCM)方法和不做散度校正(NDCM)的四种求解方案正演该模型在频率为1Hz下的模拟解.

|
图 3 垂直接触带模型解析解和三维数值解的对比 (a)模型示意图;(b)TM 模式视电阻率曲线;(c)TM 模式相位曲线. Fig. 3 Comparision of analytic calculation and 3D modeling of abutting quarter spaces model (a)Geometry of abutting quarter spaces model;(b)Apparentre sistivity of TM model;(c)Phase curve of TM model. |
图 3b和3c是频率为1 Hz时垂直接触带模型的解析解和NDCM、RPCM、RRCM 求解方案的三维数值解对比结果(DDCM 求解方案发散).由图可见,NDCM、RPCM、RRCM 三种方案的三维模拟结果与数值解的结果都比较吻合.但是RPCM、RRCM 的模拟结果是一样的,相对于NDCM 拟合效果更好,尤其在接触带附近区域显示更明显.这是由于在垂直接触带附近由于电阻率值的突变,使得在每个求解剖分单元上的磁场散度不为零.而采用RPCM、RRCM 磁场散度校正后能够有效地校正模拟的三维磁场值,使得求解结果更加准确.
4.2 低阻异常模型为了分析NDCM、RPCM、RRCM、NDCM 四种求解方案在三维大地电磁正演模拟中的计算效率,设计了一个典型低阻异常模型.低阻异常模型中低阻异常体为500m×500m×500m 的正方体、电阻率为20 Ωm,顶部埋深为500 m;围岩电阻率为200Ωm.将求解区域剖分成38×38×25格单元格,采用指数延拓增加10层空气层,频率为10Hz.
图 4 为采用三种不同散度校正方法(DDCM,RPCM,RRCM)和不进行散度校正求解(NDCM)方案迭代误差变化曲线.从图 4 中可以看出采用NDCM 方案时,误差衰减缓慢,且不能达到高精度,最大精度只能达到1×10-4.NDCM求解方案不收敛,分析主要是由于散度校正公式破坏了迭代求解的对称性,从而使方程求解发散.RPCM 和RRCM方案误差衰减曲线几乎一样,是由于两种校正方法原理一样,主要体现在速度上的差别.表 1为采用不同散度校正方法进行正演的计算时间和迭代次数,从中可以明显的看出RRCM 方案比RPCM 方案节省13.84s,大约为求解总时间的1/4.

|
图 4 不同方案正演的误差变化 Fig. 4 Error variation with scheme |
|
|
表 1 不同正演方案的计算时间和迭代次数 Table 1 Calculating time and iterations with different modeling scheme |
从以上分析可以看出,在不破坏方程求解的对称性的情况下,采用散度校正是非常必要的.散度校正一方面可以提高计算速度和精度,另一方面可以增强计算结果的准确性,这种优势在电导率突变区域尤其明显.在散度校正中,RRCM 方案相对于RPCM 方案计算速度更快,但两者的求解精度和计算结果是一样的.因此在今后的三维大地电磁正演中应采用RRCM 的散度校正方法.
为了说明RRCM 方案的适用性和稳定性,设计了6×6×4、18×18×10、38×38×25、58×58×37四种不同剖分数的三维大地电磁正演计算实例,使用的模型与上面相同.图 5为不同剖分数下RRCM散度校正正演计算时的误差衰减曲线,从图中可以看出无论剖分数如何计算误差都能快速衰减,而且曲线大致平行,说明该方案的计算是稳定的.表 2为不同剖分数的计算时间和迭代次数,表中显示随着剖分数的增加,迭代次数逐渐增加,计算时间也逐渐增加.这是由于求解元素的增加造成的.从上分析可知,RRCM 的散度校正求解方案能够稳定、快速、有效地进行三维大地电磁正演模拟.

|
图 5 不同剖分数的RRCM 散度校正正演计算误差衰减曲线 Fig. 5 The error decay curve of RRCM scheme |
|
|
表 2 不同剖分数的RRCM散度校正正演计算时间和迭代次数 Table 2 Calculating time and iterations with the RRCM with different dissection |
为了进一步说明RRCM 求解方案的稳定性和适用性,以及了解三维MT 响应的视电阻率特性,本文模拟一个复杂国际标准地电模型[21].该模型在围岩电阻率为100Ωm 的介质中含有三个异常体.异常体ρ1 为40km×5km×15km 的六面体,顶部埋深为5km,其电阻率大小为10Ωm;异常体ρ2 为15km ×25 km ×5 km 的六面体,顶部埋深为20km,电阻率大小为1Ωm;异常体ρ3 为15km×25km×30km的六面体,顶部埋深为20km,电阻率大小为10000Ωm(见表 3).图 6 为三个异常体的YZ剖面图和XY平面图,显示各个异常体的三维尺寸和空间分布.该模型的剖分数为50×48×42,采用RRCM 求解方案分别计算在0,1-10000s内21个周期(0.1,0.18,0.32,0.56,1,1.8,3.2s,…,5600s,10000s)的MT 响应.

|
图 6 国际标准模型示意图 (a)从YZ面看;(b)从XY面看. Fig. 6 Sketch of international standard model (a)YZplan view;(b)XYplan view |
|
|
表 3 异常体三个方向的延伸与电阻率值 Table 3 The extend in there direction and resistivity of anomaly body |
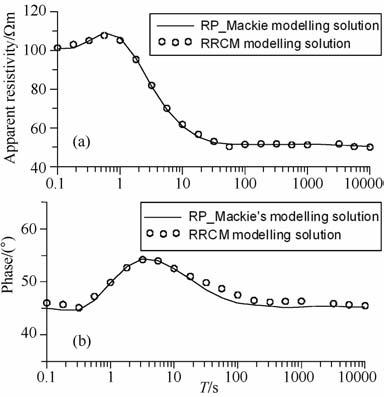
图 7 为异常体ρ1 中心点处的大地电磁测深的视电阻率和相位响应曲线.由图可见,不论是视电阻率曲线还是相位响应,RRCM求解方案的计算结果与RL_Mackcie[25]提供的结果吻合良好;进一步说明,RRCM 求解方案能够适合求解复杂的地电模型.另外,图 8为国际标准模型在1、10、100、1000s周期时视电阻率等值线图.由图可见周期为1s时没有明显视电阻率异常区,这是由于该周期的探测深度还未达到ρ1 的位置.周期为10s时可以看出一个明显长方体低阻异常区,对应着异常体ρ1.周期为100s时由于受异常体ρ2 和ρ3 影响视电阻率呈现不对称分布,可以看出低阻异常体ρ2 对视电阻率的影响明显大于高阻异常体.周期为1000s时在Y轴正向有一个延长的低阻异常体,对应着异常体ρ2 位置,但并无与高阻异常体对应的高阻异常区,同时在X轴方向两次形成一个假高阻异常区.图 9 为国际标准模型的视电阻率三维空间分布,从图中可以看出低阻异常体随着周期的逐渐增大,中心处的低阻异常区逐渐夸大;并且假的高阻异常也在逐渐变大.
|
图 7 ρ1 中心点的视电阻率(a)和相位(b)响应 Fig. 7 The response of apparent resistivity and phase in center of ρ1 |

|
图 8 国际标准模型的1,10,100,1000s周期的视电阻率等值线图 Fig. 8 Chorogram of apparent resistivity of international standard model at 1,10,100,1000s |

|
图 9 国际标准模型的电磁视电阻率响应3D 分布 Fig. 9 The response of apparent resistivity of international standard model in 3D |
由以上分析可知,大地电磁对低阻异常体的响应明显大于高阻异常体,且低阻体更容易产生假异常区.
5 结 论本文系统地讨论了大地电磁三维交错网格有限差分正演中的散度校正算法,详细推导了直接磁场散度校正(DDCM)、磁场散度残差复数校正(RPCM)、磁场散度残差实数校正(RRCM)等三种磁场散度校正方法.通过对垂直接触带模型的模拟结果与解析解对比表明,DDCM 求解方案发散,RPCM、RRCM求解方案在电阻率突变区域的拟合效果好于NDCM;从而说明合适的散度校正能够提高计算结果的精确度.对低阻地电模型的模拟结果表明,RRCM 在计算精度、迭代次数以及计算时间上均具有优势,具有收敛速度快、计算时间短、算法稳定等特点.最后采用RRCM 求解方案对国际标准模型进行模拟,结果表明RRCM 的计算结果与R L_Mackcie提供的数据非常吻合.得出主要结论如下:
(1) 在大地电磁三维交错网格有限差分正演中,在不破坏迭代求解的收敛性下进行散度校正是必要的和有效的.
(2) 在所有求解方案中,磁场散度残差实数校正(RRCM)能够稳定、快速、有效地实现三维大地电磁模拟,且该散度校正方法也能够推广到其他正演方法中.
(3) 在数值方法中,将复数方程转化为实数方程求解能够加快计算速度,数值模拟时应尽量在实数域中进行求解.
| [1] | Borner R. Numerical modelling in geo-electromagnetics: advances and challenges. Surv Geophys, 2009, 31(2): 225-245. |
| [2] | Avdeev D B. Three-dimensional electromagnetic modelling and inversion from theory to application. Surveys in Geophysics, 2005, 26(4): 767-799. |
| [3] | Osella A, dela Vega M, Lascano E. 3D electrical imaging of an archaeological site using electrical and electromagnetic methods. Geophysics, 2005, 70(4): 101-107. DOI:10.1190/1.1993727 |
| [4] | Tseng H, Lee K H, Becker A. 3D interpretation of electromagnetic data using a modified extended Born approximation. Geophysics, 2003, 68(1): 127-137. DOI:10.1190/1.1543200 |
| [5] | 张继锋, 汤井田, 喻言, 等. 基于电场矢量波动方程的三维可控源电磁法有限单元法数值模拟. 地球物理学报, 2009, 52(12): 3132–3141. Zhang J F, Tang J T, Yu Y, et al. Three dimensional controlled source electromagnetic numerical simulation based on electric field vector wave equation using finite element method. Chinese J. Geophys (in Chinese), 2009, 52(12): 3132-3141. |
| [6] | 张辉, 李桐林, 董瑞霞. 体积分方程法模拟电偶源三维电磁响应. 地球物理学进展, 2006, 21(2): 386–391. Zhang H, Li T L, Dong R X. Modeling 3-D electromagnetic responses of electric dipole using volume integral equation method. Progress in Geophysics (in Chinese) (in Chinese), 2006, 21(2): 386-391. |
| [7] | Hoversten M G, Newman G A, Geier N, et al. 3D modeling of a deepwater EM exploration survey. Geophysics, 2006, 71(5): 239-248. DOI:10.1190/1.2240113 |
| [8] | Streich R. 3D finite-difference frequency-domain modeling of controlled-source electromagnetic data: Direct solution and optimization for high accuracy. Geophysics, 2009, 74(5): 95-105. DOI:10.1190/1.3196241 |
| [9] | Avdeev D, Knizhnik S. 3D integral equation modeling with a linear dependence on dimensions. Geophysics, 2009, 74(5): 89-94. |
| [10] | Jones F W, Pascoe L J. The perturbation of alternating geomagnetic fields by three-dimensional conductivity inhomogeneities. Geophysical Journal of the Royal Astronomical Society, 1972, 27(5): 479-485. DOI:10.1111/j.1365-246X.1972.tb06103.x |
| [11] | Lines L R, Jones F W. The perturbation of alternating geomagnetic fields by an island near a coastline: reply. Canadian Journal of Earth Sciences, 1973, 10(11): 1703-1704. DOI:10.1139/e73-166 |
| [12] | Smith R S, Edwards R N, Buselli G. An automatic technique for presentation of coincident-loop, impulse-response, transient, electromagnetic data. Geophysics, 1994, 59(10): 1542-1550. DOI:10.1190/1.1443543 |
| [13] | Mackie R L, Madden T R, Wannamaker P E. Three-dimensional magnetotelluric modeling using difference equations——Theory and comparisons to integral equation solutions. Geophysics, 1993, 58(2): 215-226. DOI:10.1190/1.1443407 |
| [14] | De Groot-Hedlin C. Finite-difference modeling of magnetotelluric fields: Error estimates for uniform and nonuniform grids. Geophysics, 2006, 71(3): 97-105. DOI:10.1190/1.2195991 |
| [15] | Bergmann T, Robertsson J O A, Holliger K. Finite-difference modeling of electromagnetic wave propagation in dispersive and attenuating media. Geophysics, 1998, 63(3): 856-867. DOI:10.1190/1.1444396 |
| [16] | Zhang J, Mackie R L, Madden T R. 3-D resistivity forward modeling and inversion using conjugate gradients. Geophysics, 1995, 60(5): 1313-1325. DOI:10.1190/1.1443868 |
| [17] | Smith R S, Edwards R N, Buselli G. An automatic technique for presentation of coincident-loop, impulse-response, transient, electromagnetic data. Geophysics, 1994, 59(10): 1542-1550. DOI:10.1190/1.1443543 |
| [18] | Mackie R L, Madden T R, Wannamaker P E. Three-dimensional magnetotelluric modeling using difference equations——Theory and comparisons to integral equation solutions. Geophysics, 1993, 58(2): 215-226. DOI:10.1190/1.1443407 |
| [19] | Wang T, Hohmann G W. A finite-difference time-domain solution for three-dimensional electromagnetic modeling. Geophysics, 1993, 58(6): 797-809. DOI:10.1190/1.1443465 |
| [20] | 谭捍东, 余钦范, BookerJ, 等. 大地电磁法三维交错采样有限差分数值模拟. 地球物理学报, 2003, 46(5): 706–711. Tan H D, Yu Q F, Booker J, et al. Magnetotelluric three-dimensional modelling using the staggered-grid finite difference method. Chinese J. Geophys (in Chinese), 2003, 46(5): 706-711. |
| [21] | Tan H D, Tong T, Lin C H. The parallel 3D magnetotelluric forward modelling algorithm. Applied Geophysics, 2006, 3(4): 197-202. DOI:10.1007/s11770-006-4001-5 |
| [22] | 沈金松. 用交错网格有限差分法计算三维频率域电磁响应. 地球物理学报, 2003, 46(2): 281–289. Shen J S. Modelling of 3-D electromagnetic responses in frequency domain by using straggered-grid finite diference method. Chinese J. Geophys (in Chinese), 2003, 46(2): 281-289. |
| [23] | Saad Y. Iterative Methods for Sparse Linear Systems. Society for Industrial and Applied Mathematics, 2002 |
| [24] | d'Erceville, Kunetz. The effect of a fault on the Earth's natural electromagnetic field. Geophysics, 1962, 27(5): 651-665. DOI:10.1190/1.1439075 |
| [25] | Mackie R L, MT 3D Inversion Workshop. Dublin Test Model 1 (DTM1) responses. http://mtnet.dias.ie/workshops/2008_Dublin/dublin_3dmodel.html, 2002 |
 2011, Vol. 54
2011, Vol. 54





