声波在大气中的传播有许多应用,譬如利用无线电声系统(RASS)对大气温度场的测量[1, 2]、利用次声在大气中的长距离传播来进行核爆炸与地震信号的监测和定位[3, 4],以及最近的利用接收火山的次声波信息来反演大气的风场[5, 6]等.声波射线追踪是研究大气中声波传播的一种重要方法.射线追踪可以用来表征大气中声波的传播路径,计算声波在传播中产生的时间延迟和相位变化.这些参量对于声波雷达的目标定位、大气次声波的监测和声源位置反演等工程实践具有重要意义.
目前大气中声波的射线追踪理论主要分为两类:一种是由在理想介质中的几何光学原理、Eikonal方程出发,导出射线微分方程[7, 8];另一种是由无耗分层大气中的大气声波方程导出声(重力)波色散关系,再由Hamilton 方程组得到射线微分方程[9, 10].但是这些工作都忽略了声波在大气中的衰减效应对于射线路径的影响.虽然对于低频率的次声波而言,由于声波衰减系数较小,在短距离的传播中可以忽略声波的衰减,但是对于一般声波或存在长距离传播的低频声波而言,声波的衰减效应常常不可忽略.在实际应用中,譬如声达探测等情况,沿射线的能量衰减也具有重要意义,所以研究有耗介质中的声波射线理论有重要的意义.杨训仁最先通过推广的Hamilton方程研究大气中声波的复射线路径,但是复射线路径计算比实空间寻迹复杂得多,计算难度较大[11].
本文首先在高频近似的条件下,忽略重力项,计入大气的黏滞、热传导以及声波弛豫效应的作用,导出大气声波的局地复频散方程.再从该复数方程出发,研究声波波幅在大气中的变化和传播路径的微分方程,将复色散方程转化为实色散方程求解,形成有耗大气中的声波射线理论.最后基于MSISE00和HWM93模型[12, 13]给出的大气背景参数剖面,对有耗大气和无耗大气中声波的射线轨迹进行了数值模拟,结果表明在远场传播情况下,大气损耗对声波射线轨迹具有明显的影响.
2 理论模型 2.1 局地频散方程在大气中,描述大气运动的动力学方程组可以表示为[9, 11, 14]
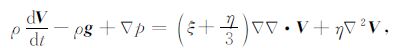
|
(1) |
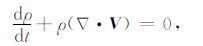
|
(2) |
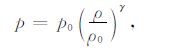
|
(3) |
其中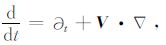
将方程中的参量表征为背景值(使用下标0 标注)和声波扰动值(使用下标1标注)之和:
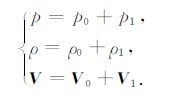
|
(4) |
并在水平分层的假设下对方程组做简化处理.由于研究的对象是无旋的寻常声波,有 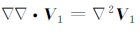
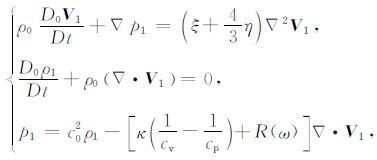
|
(5) |
式中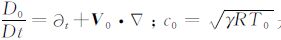
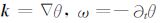
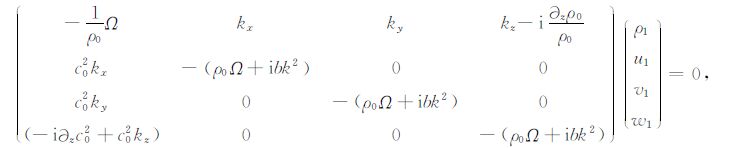
|
(6) |
(6) 式中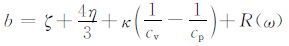
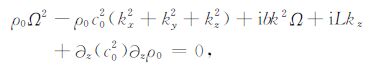
|
(7) |
这里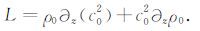
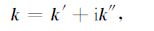
|
(8) |
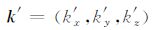
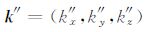
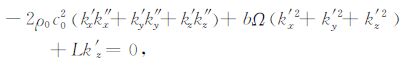
|
(9) |

|
(10) |
从(9)式即色散方程的虚部中,求解k″,以描述大气中声波沿射线方向上波幅的变化;将k″的值代入色散方程的实部(10)式,再利用Hamilton 方程组,就可以导出耗散大气中声波的射线方程组.
2.2 声波的衰减和膨胀声波在等温大气中传播时,会受到大气衰减的作用,且由于大气的密度存在不均匀性,在铅直方向上会有值为1/(2H)的幂指数形式的增长因子,H为等温大气中的标高[9].基于这种认识,可以得到在有耗的水平分层大气中,声波波矢的虚部与波动振幅空间中的衰减和竖直方向上的增长有关,设声波衰减系数为α,增长因子为β,则有
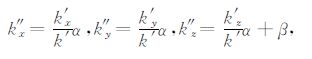
|
(11) |
即,x、y方向上的虚波数为耗散系数在该方向上的分量,z方向上的虚波数为耗散系数在该方向上的分量和增长因子的组合.
将(11)式代入色散关系的虚部方程(9)式中,会得到衰减系数和增长因子构成的方程.可以解得衰减系数和增长因子分别为
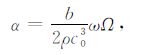
|
(12) |
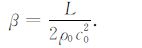
|
(13) |
(12) 式中Ω 代表大气运动对于声波衰减的影响.这表明在实际的声波传播中,风的作用会使得单位时间内的声程发生改变,继而影响声波的衰减程度.在静止大气中,Ω 变为ω,在忽略弛豫作用R(ω)的情况下,衰减系数退化成黏滞和热传导导致的经典声波衰减系数.
(13) 式表明声波在大气中传播时,在能流恒定的情况下,在竖直方向上会存在由温度梯度和密度梯度造成的声波波幅的变化,具体表现为当声波从密度大的介质到密度小的介质传播的时候,声波波幅的膨胀或者从密度小的介质到密度大的介质时波幅的压缩.在等温大气中,声波波幅的增长因子退化为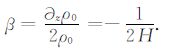
在实际计算中声波衰减的规律比较复杂,所以可以通过实际大气中总的吸声系数,来确定实际声波射线计算中的b的值.实际中,静止大气的声吸收由若干机制组成,各个机制的声波衰减具有良好的线性叠加性质:

|
(14) |
αcl 是由黏性和导热性引起的经典部分,它是温度、压强和频率的函数;αrot 是转动受激分子弛豫过程引起的转动弛豫部分,振动受激分子弛豫过程引起的振动弛豫部分.这些参数的经验表达为[14]
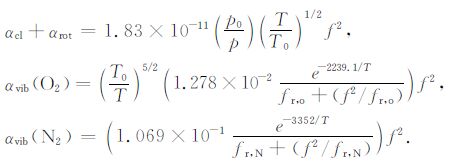
|
(15) |
此处衰减系数的单位都为Np, 其中fr, o 和fr, N 分别代表氧气分子和氮气分子的振动弛豫频率:
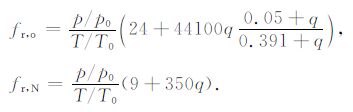
|
(16) |
q为比湿,当给定湿压e的情况下,有q=100$\frac{e}{p}$.T是绝对温度(T0 =293 K),p为大气的压强(p0 =101325N/m2).
通过经验公式(15)~(16),在已知大气背景参数的情况下,可以给出无风情况下的声波衰减参数,由此,可以将介质衰减系数b表征为
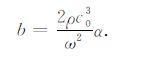
|
(17) |
由表达式(14)~(17)可知,b与水汽压、温度、压强、声波频率等因素有关.所以在实际计算中,利用(14)~(17)式可以给出参数b.通过真实大气的衰减值来修正b,射线理论可以较为完全地计入声波衰减在声波色散关系里面的贡献,从而在射线方程中更加精确地进行路径轨迹的计算.
2.3 声波的射线微分方程将复波数的虚部求解的结果(11)、(12)、(13)式代入色散关系的实部(10)式当中,则得到耗散介质中高频声波的实色散关系为
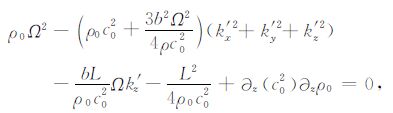
|
(18) |
此时,色散关系已经变成了一个实数方程,可以应用经典的射线方程求解方法[9, 10],通过Hamilton方程组来求解,
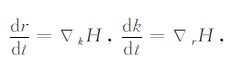
|
(19) |
将实数色散关系代入(19)式中求解,则有射线微分方程:
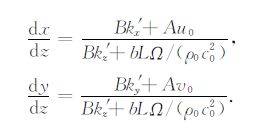
|
(20) |
对于空间中的波数,则有
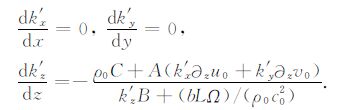
|
(21) |
式(20)和(21)中,
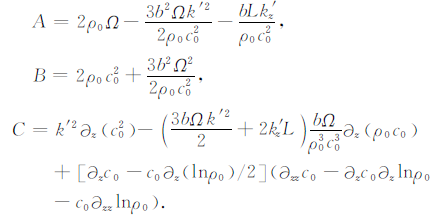
|
(22) |
在给出大气的温度场和风场剖面以及空间中的水汽分布的情况下,利用(20)~(22)式,就可以算出包含耗散贡献的声波在大气中的射线轨迹.
3 数值模拟结果与分析为了表明在有耗情况声波的衰减对声波轨迹的改变,我们在相同的背景下,将无耗和有耗两种情况下的计算结果进行对比和分析.讨论分两种情况:近场声波传播和远场声波传播.声场计算中的大气背景由MSISE00和HWM93来描述.
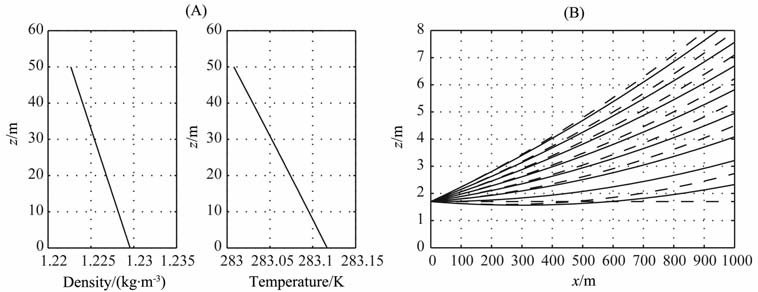
3.1 近场声波传播在无风的情况下,设定大气的背景参数为图 1A所示,此时地表的水汽压为22hPa.在该背景条件下,设声波频率为1500 Hz, 设定相同的发射角度,分别计算考虑有耗和无耗两种情况下的射线描迹结果,如图 1B所示.
|
图 1 A)大气的密度和温度剖面.(B)射线描迹,实线表示考虑耗散的射线结果, 虚线表示无耗散的射线结果,发射仰角从一0.05°〜0.3°以0.05°为步进 Fig. 1 (A) Atmospheric profiles of density and temperature. (B) The ray trace. Solid line is calculated by the lossy theory. Dash line is calculated by lossless theory.Shooting angles vary from —0. 05°〜0. 3°with a step of 0. 05° |
从图 1B中可以看出,忽略耗散计算出的声射线在水平分层的条件下,当发射角度为0°时,无法产生偏折效应,这是由于忽略耗散的射线方程在竖直方向上的波矢分量k′z=0处不解析导致的,显然,这是无耗射线理论的一个不足之处.有耗射线理论可以弥补这个不足.从(21)式可以看出,耗散项的存在使得射线微分方程在波矢分量kz′= 0 时同样解析.从图 1B上也可以看到,发射角为0°的射线和其他射线的位置关系比较合理,符合射线族变化的整体趋势.
大部分无耗射线理论计算的声波射线在传播了一定距离之后,除了发射角为0°的射线,与有耗射线相比,轨迹偏高.这说明在真实大气中,耗散作用使得声波的射线产生下移的效果.这种偏移的误差在图中可以看到,1500 Hz的声波在传播了水平距离1000 m 之后,声波轨迹与无耗射线理论计算的轨迹存在着10-1m 级的误差.这种误差相对于近场声波定位精度而言,量值较小.这表明在近场声场计算中,声波的衰减对声波的传播路径的影响较小,可以忽略.
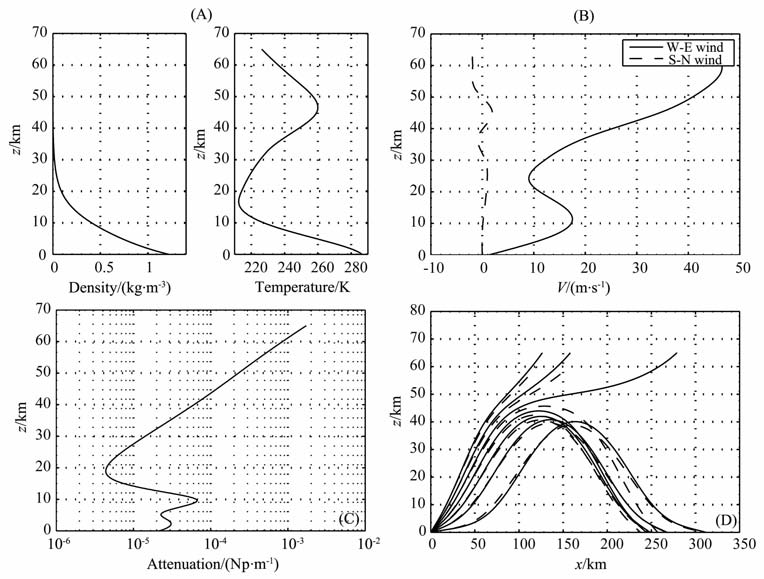
3.2 远场声波传播由于在远场传播的情况下,风场是导致声线偏折的重要因素,所以射线计算考虑风场的影响.大气背景参数给定如下:图 2A 为大气的密度和温度剖面(通过MSISE00给定),图 2B为大气的风场剖面(通过HWM93给定).选取发射声波的频率为100Hz, 地表水汽压为12hPa, 声波的发射方向为正东方向,仰角从4°~24°,以4°为步长步进.通过模拟计算,得到大气中该频率声波的耗散系数随高度的分布和大气中的射线轨迹,即图 2C 和图 2D.在图 2D中分别给出了考虑耗散(用实线表示)和忽略耗散(用虚线表示)两种情况下所计算出的声线轨迹.
|
图 2 A)大气的密度和温度剖面.(B)大气的风场剖面.(C) 100 Hz声波在大气中的衰减系数随高度的分布.(D)射线描迹,虚线为无耗散计算结果,实线为考虑耗散计算结果.发射仰角为4°〜28°,以4°为步进 Fig. 2 (A) Atmosphericprofiles of densityand temperature. (B) Atmospheric profiles of wind. (C) The profiles of absorption coefficient of 100 Hz. (D) The ray trace. Solid line is calculated by the lossy theory. Dash line is calculated by lossless theory. Shooting angles vary from4°〜28°with a step of 4° |
从图 2D 中可以看到,无论是考虑不计耗散还是考虑耗散效应,计算所得声线的类型从传播上可以分为两种类型.一种是以较低仰角发射,经过中低层大气的折射作用,最终发生全反射,又回到了地表,这种情况可以称为低仰角模式;一种是以较大的仰角发射,大气对声波的折射效应不足以使声波在中低层大气被反射,最后入射到60km 以上的中高层大气,进入电离层区域中,这种情况可以称作高仰角模式.其中,低仰角模式的声线是大气声波远距离传播的一种常见情况,常常被称为声波的“异常传播".
在无耗散情况计算的声线中,发射角度为4°~20°的射线属于低仰角模式,而在考虑耗散情况计算的声线中,属于低仰角模式的声线为发射仰角在4°~16°的射线.对于在低仰角模式和高仰角模式过渡区间的发射角,如图 2D 中发射角为20°的两条射线,可以看到,考虑耗散效应所计算的声线属于高仰角模式,忽略耗散计算的声线属于低仰角模式.从这两条射线的对比当中可以看到,声波衰减可以导致射线计算结果存在传播模式的不同.
在相同的发射角度下,对比有耗和无耗这两种情况下所计算的声波射线,可以发现声线轨迹误差较为明显.在射线轨迹的上升区域,即kz′>0时,在低层大气的对流层中,考虑耗散计算的声波射线略低于忽略耗散的射线,而在较高的平流层区域中,考虑耗散计算的射线则略高于忽略耗散的射线,这种现象在发射角较小的情况比较明显.在相同发射角度的低仰角模式下,两种声波射线轨迹的落地点处可以有101km 量级的误差.所以在远距离声波传播的精确计算中,考虑声波衰减的作用是必要的.
4 结论文章通过大气中的线性声波扰动方程组,得到了在高频近似下的,包含黏滞、热传导和弛豫等声波衰减和色散效应的局地复色散关系.通过求解该色散关系的虚部,导出声波在大气传播过程中声波波幅变化的虚波数,它可以由声波的衰减系数和增长因子来表示.特别的,文章通过真实大气中的声波衰减系数对色散关系中的耗散参量进行修正,以便更准确地描述真实大气的衰减性质及其对声波传播轨迹的贡献.对该色散关系的实部,应用Hamilton方程组来求出声波在考虑耗散情况下的射线微分方程组.当存在有大气密度和温度梯度时,射线方程将对于所有波数处处解析,声波射线计算模型有良好的计算稳定性.
在一定的大气背景下,通过对有耗和无耗这两种射线追踪理论的数值计算结果的对比,可以看到在大气中,声波的衰减对声波的射线路径会产生一定的影响.在近场声波传播中,考虑耗散效应的声射线要比忽略耗散的声射线略低,但误差不是很大;在远场的时候,这种误差会变大,特别是对于高仰角模式和低仰角模式之间的过渡区域的发射角而言,考虑耗散和不考虑耗散两种理论会计算出不同模式的声线,产生巨大的偏差.所以,在频率较低、传播距离较近的声波射线轨迹计算中,使用无耗的射线追踪理论是可行的;但是在声波传播距离较远或声波的频率较高的时候,声波衰减对于射线路径的影响较大,有必要应用考虑耗散效应的射线理论来更精确地计算声波射线.
| [1] | Matuura N, Masuda Y, Inuki H, et al. Radio acoustic measurement of temperature profile in the troposphere and stratosphere. Nature , 1986, 323: 426-428. DOI:10.1038/323426a0 |
| [2] | Masuda Y. Influence of wind and temperature on the height limit of a radio acoustic sounding system. Radio. Sci. , 1988, 23(4): 647-654. DOI:10.1029/RS023i004p00647 |
| [3] | Bedard A J, Georges T M. Atmospheric Infrasound. Phys. Today , 2000, 53(3): 32-37. DOI:10.1063/1.883019 |
| [4] | Le Pichon A. Infrasound associated with 2004-2005 large Sumatra earthquakes and tsunami. Geophys. Res. Lett. , 2005, 32: L19802. |
| [5] | Le Pichon A, Ceranna L, Garcés M, et al. On using infrasound from interacting ocean swells for global continuous measurements of winds and temperature in the stratosphere. J. Geophys. Res. , 2006, 111: D11106. DOI:10.1029/2005JD006690 |
| [6] | Le Pichon A, Blanc E, Drob D. Probing high-altitude winds using infrasound. J. Geophys. Res. , 2005, 110: D20104. DOI:10.1029/2005JD006020 |
| [7] | Virieux J, Garnier N, Blanc E, et al. Paraxial ray tracing for atmospheric wave propagation. Geophys. Res. Lett. , 2004, 31: L20106. DOI:10.1029/2004GL020514 |
| [8] | Dessa J X, Virieux J, Lambotte S. Infrasound modeling in a spherical heterogeneous atmosphere. Geophys. Res. Lett. , 2005, 32: L12808. |
| [9] | Yeh K C, Liu C H. Acoustic-gravity waves in the upper atmosphere. Rev. Geophys. Space Phys. , 1974, 12(2): 193-216. DOI:10.1029/RG012i002p00193 |
| [10] | 丁锋, 万卫星, 袁洪. 耗散大气中水平不均匀风场对内重力波传播的影响. 地球物理学报 , 2001, 44(5): 589–595. Ding F, Wan W X, Yuan H. The effect of inhomogeneous winds on internal gravity wave propagation in a dissipative atmosphere. Chinese J. Geophys. (in Chinese) (in Chinese) , 2001, 44(5): 589-595. |
| [11] | 杨训仁. 损耗大气的射线理论. 声学学报 , 1986, 11(2): 65–73. Yang X R. Ray theory for lossy atmosphere. Acta Acust. (in Chinese) , 1986, 11(2): 65-73. |
| [12] | Hedin A E. Empirical wind model for the upper, middle and lower atmosphere. J. Atmos. Terr. Phys. , 1996, 58: 1421-1447. DOI:10.1016/0021-9169(95)00122-0 |
| [13] | Hedin A E. Extension of the MSIS thermospheric model into the middle and lower atmosphere. J. Geophys. Res. , 1991, 96: 1159-1172. DOI:10.1029/90JA02125 |
| [14] | 杨训仁, 陈宇. 大气声学. 北京: 科学出版社, 2007 . Yang X R, Chen Y. Atmospheric Acoustics (in Chinese) (in Chinese). Beijing: Science Press, 2007 . |
| [15] | Jiang Z Y, Greenleaf J F. The nonlinear interaction of two plane waves in a viscous medium. J. Acoust. Soc. Am. , 1996, 99(5): 2783-2790. DOI:10.1121/1.414816 |
| [16] | Brown E H, Hall F F. Advances in Atmospheric Acoustics. Rev. Geophys. Space Phys. , 1978, 16(1): 47-110. DOI:10.1029/RG016i001p00047 |
 2011, Vol. 54
2011, Vol. 54


