随钻感应测井作为随钻测井技术的重要组成部分,由于采用的频率较低,与传统的随钻电磁波传播电阻率测井技术相比具有探测深度更深、在高阻地层中测量精度更高、不受地层介电常数影响等优点,因而具有广阔的应用前景[1].除此之外,随钻感应测井数据还可以直接与标准的电缆感应测井数据进行对比,使测量结果能更方便地融入现有的数据解释体系,从而达到更精确地评价地层和描述油藏的目的.最具代表性的随钻感应测井仪器是英国Geolink公司的TRIM[1~5],该仪器将轴向线圈系置于钻铤旁侧的V 型凹槽内,采用20kHz的低频感应频率,因而具有比常规随钻电磁波电阻率测井更深的探测深度.由于接收信号主要来自于V 型凹槽一侧地层的贡献,因而该仪器具备了方位探测能力(图 1).置于V 型凹槽内的线圈系直径比常规电缆感应测井仪器的线圈系直径要小,以便于安装.为了消除钻铤产生的误差,在V 型槽的壁上覆盖有由高电导率材料制成的电磁反射层,该反射层将槽内的发射或接收线圈系从钻铤的影响中屏蔽起来.V 型槽内线圈系与反射层之间的空间填充有高强度绝缘介质,可以使线圈系免于受井眼内泥浆的冲击与磨损.由于钻铤上V 型凹槽的存在,该仪器是偏心的、非轴对称的,对其响应和探测特性进行数值模拟具有较大困难,尤其是线圈系与电磁反射层之间强烈的相互作用使情况变得更为复杂.所有的二维或适用于轴对称性情况的数值模拟技术[6]不再适合上述模型.矢量有限元[7]和有限差分法[8]等三维数值模拟算法在模拟考虑钻铤影响的情况下传统随钻仪器在井眼中偏心或在复杂地层中的电磁响应时均将圆柱形钻铤作为理想的导体边界处理,而体积分方程[9~13]在模拟上述复杂地层模型中随钻仪器或多分量感应测井仪器的电磁响应时均忽略钻铤或金属心轴的影响.由于V 型槽的存在,TRIM 仪器的钻铤不再是圆柱形,不能将其作为圆柱形理想导体边界处理,又由于钻铤与地层的电导率对比度太大,也不能将其作为介质处理.这些因素使得上述三维电磁场数值模拟方法也不能有效使用.笔者曾开发了圆柱坐标系下径向成层介质中磁流源并矢Green函数的矢量本征函数展开式[14],研究线圈系在圆柱形钻铤外侧时的响应特性.本文中笔者将V 型槽壁上的高电导率反射层视为理想导体,除V 型槽外将钻铤的其他部分视为完纯导电劈,采用圆柱坐标系下针对完纯导电劈模型的磁流源并矢Green函数的矢量本征函数展开式[15]对随钻感应测井仪器在径向成层地层中的响应和探测特性进行数值模拟,有效地克服了传统的数值模拟方法所遇到的困难.除模拟传统感应测井仪器的响应外,本文还采用上述方法模拟了V型槽内多分量感应测井仪器的响应特性.

|
图 1 仪器模型截面图 Fig. 1 Sectional view of tool model |
设完纯导电劈的张角为φ0,则线圈系所在的V型槽的张角为2π-φ0,V 型槽的边界分别位于φ =0和φ =2π-φ0 处(图 1).采用圆柱坐标系并假设发射源随时间的变化关系为exp(-iωt),其中ω 为角频率.设在V 型槽内场点的位置坐标为R(r,φ,z),源点的位置坐标为R′(r′,φ′,z′).
2.1 完纯导电劈的M类和N类矢量本征函数在圆柱坐标系下可采用分数阶的M类和N类矢量本征函数表示完纯导电劈模型的磁流源并矢Green函数.由文献[15],M类和N类矢量本征函数的奇函数和偶函数分别定义为
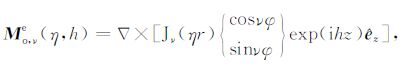
|
(1a) |
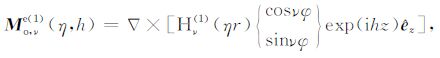
|
(1b) |
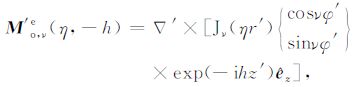
|
(1c) |
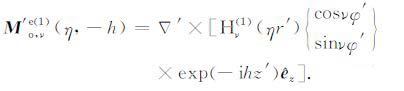
|
(1d) |

|
(2a) |
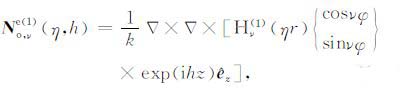
|
(2b) |
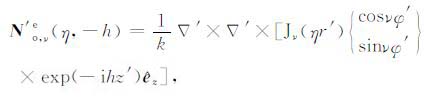
|
(2c) |
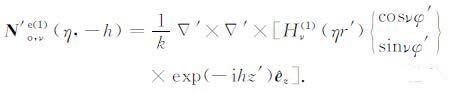
|
(2d) |
式中,k2 =ω2με,μ 为V 型槽内均匀介质的磁导率,ε为V型槽内均匀介质的复介电常数,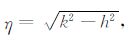
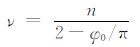
将式(1)和(2)展开可以发现,上述针对完纯导电劈模型的M类和N类矢量本征函数在边界φ =0和φ =2π-φ0 处满足下列边界条件:
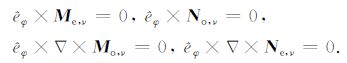
|
(3) |
由文献[15],V 型槽内均匀介质中磁流源磁型并矢Green函数GHM(R,R′)的矢量本征函数展开式为
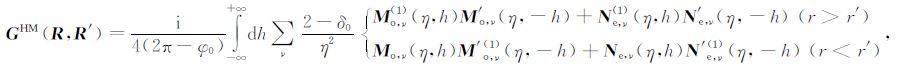
|
(4) |
式中,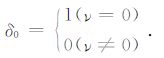
根据M类和N类矢量本征函数之间的关系,V 型槽内均匀介质中磁流源电型并矢Green函数GEM(R,R′)的矢量本征函数展开式为:
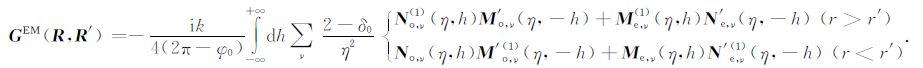
|
(5) |
编程计算时需利用式(1)和(2)将式(4)和(5)展开,从而得到并矢Green函数的所有分量.式(4)和(5)展开后的详细表达式见附录A.
2.3 V型槽内径向成层介质中的磁流源并矢Green函数
在对含井眼、侵入带、原状地层的复杂地层模型进行数值模拟时,需采用径向成层介质的磁流源并矢Green函数.设多层圆柱形径向成层介质由内向外共有m层,各层界面半径分别为r1、r2、…、rm-1,每层介质的参数分别为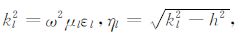
当场点位置在第1层时:
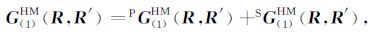
|
(6a) |
式中背景项PG(1)HM(R,R′)由式(4)取第1层的电性参数得到,散射项SG(1)HM(R,R′)可类比式(4)由下列表达式得到:
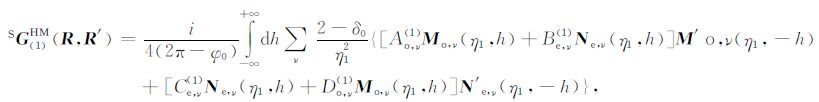
|
式中,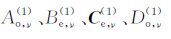
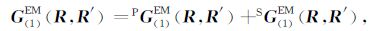
|
(6b) |
式中背景项PG(1)EM(R,R′)由式(5)取第1层的电性参数得到,散射项SG(1)EM(R,R′)可类比式(5)由下列表达式得到:
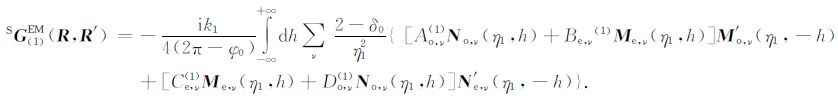
|
当场点位置在第l层(1<l< m)时,GHM 和GEM 只包含散射项:
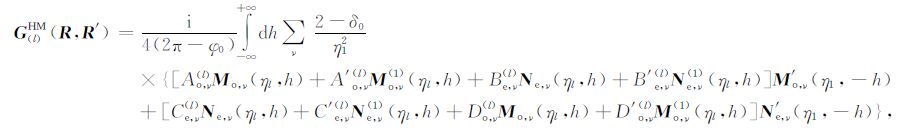
|
(6c) |
式中

|
(6d) |
当场点位置在第m层时,GHM 和GEM 只包含散射项:
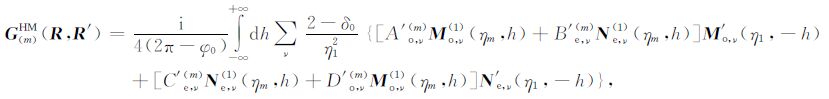
|
(6e) |
式中
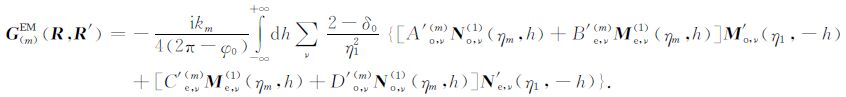
|
(6f) |
在式(6)的各表达式中,待定系数由圆柱形界面r1、r2、…rm-1 处GHM(R,R′)和GEM(R,R′)所满足的下列边界条件得到: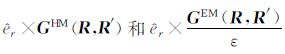
将发射源视为磁偶极子,由式(6)可得到沿任意方向放置的发射源在V 型槽内任意层介质中产生的电场强度、磁场强度和接收线圈的感应电动势[14],并进而获得地层的视电导率[16].利用式(6)除了可以模拟传统感应测井仪器的响应外,还可以模拟V 型槽内多分量感应测井仪器在径向成层地层中的响应[17, 18].
3 数值计算及讨论在模拟随钻感应测井仪器的响应时取发射频率为20kHz、发射线圈匝数为50、发射电流强度为1A、线圈系直径为1cm.线圈系可沿$\hat{e}$r、$\hat{e}$φ、$\hat{e}$z方向放置.
3.1 V 型槽张角对电磁场分布的影响计算发射线圈产生的电磁场时假设发射线圈的径向坐标为3cm、方位坐标为V 型槽张角的一半,取V 型槽内均匀分布绝缘介质的电参数为自由空间中的数值.图 2和图 3为当V 型槽的张角2π-φ0取不同的值时(张角为360°表示无钻铤存在)距发射线圈轴向距离0.5 m、与发射源相同方位角处电场强度和磁场强度不同分量的幅值随场点径向坐标r的变化关系.由图 2和图 3可以看出,当发射线圈沿$\hat{e}$z方向放置时,随着V 型槽张角的减小,电磁场的幅度逐渐增加,这是由于V 型槽壁上理想导体反射层的强烈反射作用导致信号加强造成的.该结论说明上述钻铤结构可以增加仪器轴向线圈系的径向探测深度且V 型槽的张角越小越好.另外,将V 型槽张角为180°时上述矢量本征函数展开式的计算结果与采用镜像法得到的结果进行比较,二者完全一致,说明了本文算法的正确性.当发射线圈沿$\hat{e}$r方向放置时,若无钻铤存在,则电磁场的幅度值最大,当V 型槽的张角为180°时电磁场的幅度值最小,此后随着V 型槽张角的减小电磁场的幅度逐渐增加.当发射线圈沿$\hat{e}$φ 方向放置时,在V 型槽的张角为180°时电磁场的幅度值最大,此后随着V 型槽张角的减小电磁场的幅度值也逐渐减小.上述结论亦可以采用镜像法通过进行定性分析得到.

|
图 2 V型槽张角不同时电场强度的幅值随径向坐标r的变化关系 Fig. 2 Relation between the magnitude of electric fields and radial coordinate r for different angles of the V-shaped channel |

|
图 3 V型槽张角不同时磁场强度的幅值随径向坐标r的变化关系 Fig. 3 Relation between the magnitude of magnetic fields and radial coordinate r for different angles of the V-shaped channel |
由图 3d,对同一径向坐标,由于|Hzz|随V 型槽张角的减小而增加,因此若像TRIM 那样在V 型槽内只沿轴向放置传统的随钻感应测井仪器,则V型槽的张角越小越好,可以最大限度地增加信号强度.由图 3a,当V 型槽的张角小于180°时,|Hrr|亦随V 型槽张角的减小而增加,因此若在V 型槽内放置的多分量随钻感应测井仪器只测量Hrr和Hzz两个主分量,则V 型槽的张角越小越好.但由图 3c,|Hφφ| 却随着V 型槽张角的减小而减小,因此若在V 型槽内放置的多分量随钻感应测井仪器除测量Hrr和Hzz两个主分量外还测量|Hφφ| 这个主分量,则V 型槽的张角并非越小越好,否则|Hφφ| 分量就会因为信号强度太弱而无法探测到.在此情况下需对V 型槽张角的取值进行折衷考虑,同时兼顾到Hzz、Hrr和|Hφφ| 三个主分量的强度,使它们的强度越接近越好.
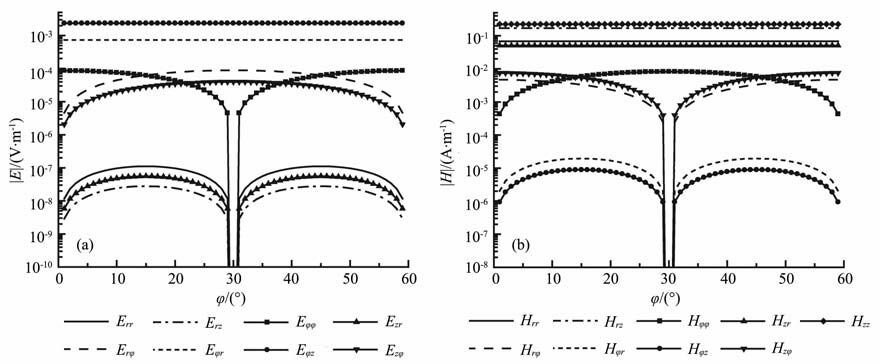
3.2 电磁场分布对方位角的依赖关系设V型槽张角为60°,多分量感应测井仪器发射线圈的径向坐标为5cm、方位角坐标为30°,仍取V 型槽内均匀分布绝缘介质的电参数为自由空间中的数值.图 4为距发射线圈轴向距离0.2m、径向坐标为0.1m处电磁场强度的各分量随场点方位角坐标φ 的变化关系.由图 4可以看出,电磁场强度的不同分量对方位角的依赖程度是不同的.除Eφr分量和Eφz分量外,电场强度的其他分量均随着方位角有明显变化,而磁场强度的Hrr、Hrz、Hzr、Hzz则并不明显依赖于方位角的变化.
|
图 4 V型槽张角为60°时电磁场强度随方位角p的变化关系 Fig. 4 Relation between the magnitude of electromagnetic fields and azimuth angle when theV-shaped channel's angle is 60° |
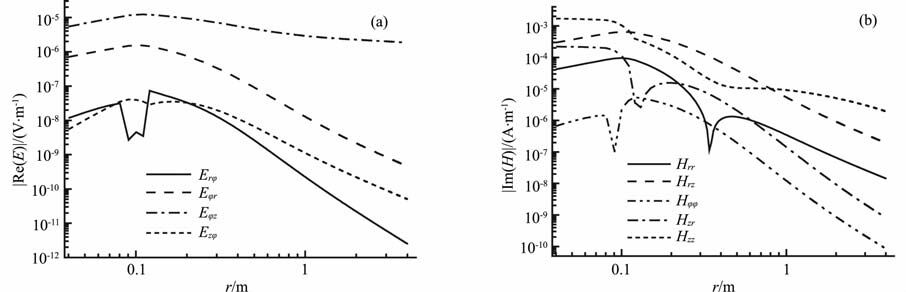
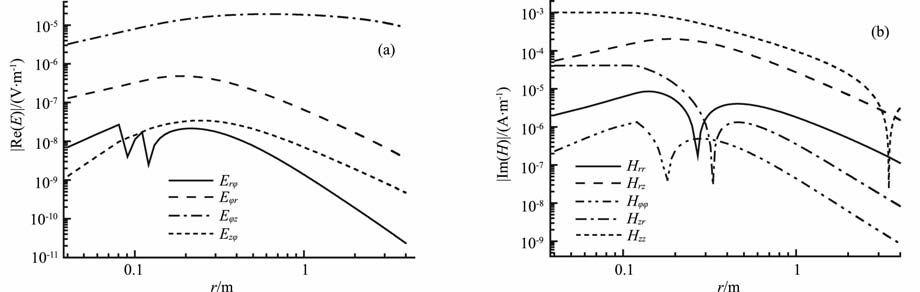
仍取V 型槽张角为60°,设发射线圈的径向坐标为3cm、方位角坐标为30°,包围线圈系的绝缘介质的半径为8.5cm、井眼半径为12cm.图 5为井眼泥浆电导率10S/m、地层电导率0.1S/m 时距发射线圈轴向距离0.2 m、与发射源相同方位角处电磁场几个分量的强度随场点径向坐标r的变化关系.图 6为井眼泥浆电导率0.1S/m、地层电导率1S/m时距发射线圈轴向距离0.2 m、与发射源相同方位角处电磁场几个分量的强度随场点径向坐标r的变化关系.根据图 4,电场强度的所有8个分量中只有4个分量在方位角坐标为30°处不为零,磁场强度的所有9个分量中有5个分量在方位角坐标为30°处不为零,故图 5和图 6 所给出的是非零分量.另外,由于电场强度的实部和磁场强度的虚部能明显反映地层信息,故图 5和图 6 给出的是电场强度的实部和磁场强度的虚部.由图 5a和图 6a可以看出,在地层界面处电场强度的法向分量Erφ 发生突变,而其他三个分量由于属于切向分量故在地层界面处仍保持连续.由于假设地层是非磁性的,故由图 5b和图 6b可以看出磁场强度的各分量在地层界面处仍保持连续.
|
图 5 井眼电导率10S/m、地层电导率0.1S/m时电磁场强度随径向坐标r的变化关系 Fig. 5 Relation between the magnitude of electromagnetic tields and radial coordinate r when the conductivities of the borehole and formation are 10 S/m and 0.1 S/m |
|
图 6 井眼电导率0. 1S/m、地层电导率1. 0S/m时电磁场强度随径向坐标r的变化关系 Fig. 6 Relation between the magnitude of electromagnetic fields and radial coordinate r when the conductivities of the borehole and formation are 0.1 S/m and 1.0 S/m |
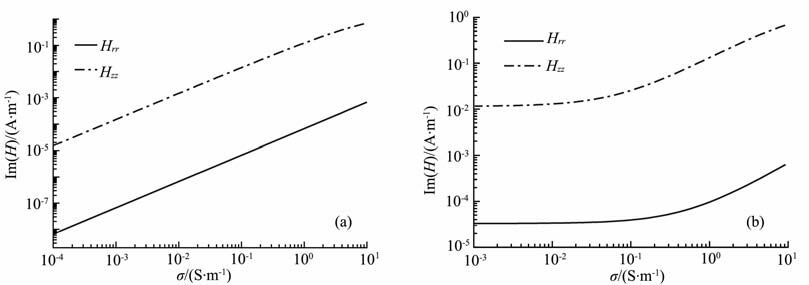
取V 型槽张角为30°,设发射线圈的径向坐标为3cm、方位角坐标为15°,包围线圈系的绝缘介质的半径仍设为8.5cm、井眼半径为12cm,并假设发射线圈的磁偶极矩为1Am2.接收线圈与发射线圈的径向坐标和方位角坐标均相同,距发射线圈的轴向距离为1m.图 7a为无井眼情况下接收线圈处磁场强度两个主分量Hrr和Hzz的虚部随均质地层电导率的变化关系,该图可以作为标准值用于对实际地层中接收信号的刻度从而获得实际地层的视电导率.对于不同的V 型槽张角,由于接收信号的强度是不同的,故用于刻度的标准值也不同.由图 7a,两个主分量Hrr和Hzz随均质地层电导率的变化规律是相同的.图 7b为井眼泥浆电导率10S/m 时接收线圈处磁场强度两个主分量的虚部随地层电导率的变化关系.由图 7b,由于低阻泥浆电导率的存在,当地层电导率值较低时接收信号偏大,视电导率增加.另由该图可知,井眼泥浆电导率对Hrr和Hzz两种不同信号的影响规律是相同的.由于V型槽的张角很小,由图 3知|Hφφ| 信号的数值太小,无法精确探测到,故图 7没有给出|Hφφ| 曲线.
|
图 7 V型槽张角为30°时磁场强度的虚部随地层电导率的变化关系 (a)无井眼;(b)有井眼. Fig. 7 Relation between the imaginary part of magnetic fields and formation conductivity when theV-shaped channel's angle is 30° (a) Without considering borehole; (b) Considering borehole. |
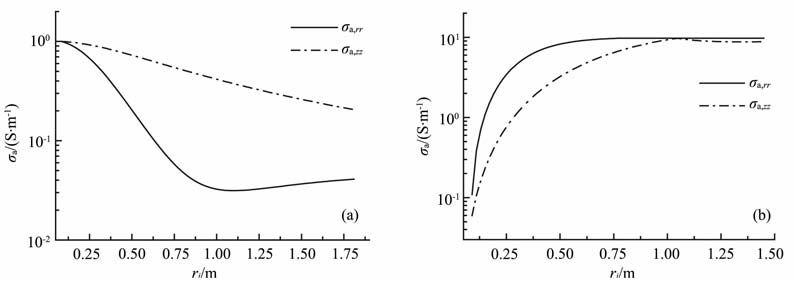
首先取V 型槽张角为30°,取发射线圈的径向坐标为3cm、方位角坐标为15°,包围线圈系的绝缘介质的半径仍设为8.5cm,忽略井眼的存在,假设发射线圈的磁偶极矩仍为1Am2.仍假设接收线圈与发射线圈的径向坐标和方位角坐标均相同且距发射线圈的轴向距离为1 m.图 8a为侵入带电导率0.05S/m、地层电导率1S/m(高阻侵入)时视电导率的两个主分量σa,rr和σa,zz随侵入半径的变化关系,图 8b为侵入带电导率10S/m、地层电导率0.05S/m(低阻侵入)时视电导率的两个主分量σa,rr和σa,zz随侵入半径的变化关系,视电导率的刻度以图 7a的数据作为标准值.由图 8,当侵入半径较小时,无论是σa,rr还是σa,zz均与地层电导率接近,接收信号主要反映地层的电导率信息.随着侵入半径的增加,侵入带电导率的影响逐渐增大,σa,rr和σa,zz逐渐趋向于侵入带的电导率.但对比σa,rr和σa,zz的变化速度可以看出,σa,rr随侵入半径的变化比σa,zz快,即σa,rr能在更小的侵入半径处达到侵入带电导率.这说明侵入带电导率对σa,rr和σa,zz的影响程度是不同的,其对σa,rr的影响大于对σa,zz的影响.工程上一般将侵入带电导率σxo 和地层电导率σt 的平均值即σa =0.5(σxo +σt)对应的侵入直径定义为径向探测深度[19],则图 8a中高阻侵入情况下σa,rr和σa,zz的径向探测深度分别为0.63m 和1.58m,图 8b中低阻侵入情况下σa,rr和σa,zz的径向探测深度分别为0.62m和1.28 m.这说明σa,rr的径向探测深度比σa,zz浅,主要反映近井眼地层的信息,而由σa,zz可以获得距离井眼较远地层的信息.
|
图 8 V型槽张角为30°时视电导率随侵人半径的变化关系 (a)髙阻侵人;(b)低阻侵人. Fig. 8 Relation between the apparent conductivity and radius of invasion when theV-shaped channel's angle is 30° (a) Iligh-resistivity invasion; (b) Low-resistivity invasion. |
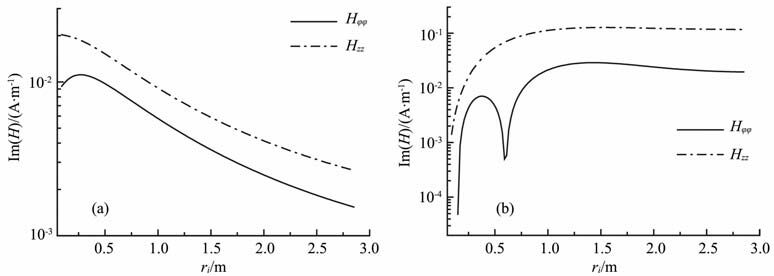
再取V 型槽张角为180°,发射线圈和接收线圈的方位角坐标均为90°,其余参数不变.图 9(a,b)分别为高阻侵入和低阻侵入情况下接收线圈处磁场强度两个主分量|Hφφ| 和Hzz的虚部随侵入半径的变化关系.由图 3知当V 型槽张角为180°时|Hφφ| 达到最大而Hrr达到最小,故图 9没有给出Hrr曲线.
|
图 9 V型槽张角为180°时磁场强度的虚部随侵人半径的变化关系 (a)髙阻侵人;(b)低阻侵人. Fig. 9 Relation between the imaginary part of magnetic fields and radius of invasion when the V-shaped channel's angle is 180° (a) Iligh-resistivity invasion; (b) Low-resistivity mvasion. |
(1) 采用圆柱坐标系下针对完纯导电劈模型的磁流源并矢Green函数的矢量本征函数展开式,可有效地计算钻铤V 型槽内传统感应测井仪器和多分量感应测井仪器在径向成层地层中的响应和探测特性,克服了传统数值模拟方法所遇到的困难.
(2) V 型槽张角的变化对电磁场不同分量的影响规律不同.若只采用传统的随钻感应测井仪器进行测量,V 型槽的张角可尽量小一些以最大限度地增加信号强度.若采用多分量随钻感应测井仪器进行测量,需对V 型槽张角的取值进行折衷考虑.由于在具有不同张角的V 型槽内接收信号的强度不同,在对地层视电导率进行刻度时需根据V型槽张角确定标准值.
(3) 电磁场不同分量对方位角的依赖程度不同.在V 型槽内除Eφr和Eφz外电场强度的其他分量均随方位角变化明显,除Hrr、Hrz、Hzr和Hzz外磁场强度的其他分量均随方位角变化明显.
(4) 侵入带电导率对不同分量接收信号的影响程度不同,因而不同分量接收信号的径向探测深度不同.
附录A:V 型槽内均匀介质中并矢Green函数各分量的表达式当r>r′ 时,式(4)的展开形式为
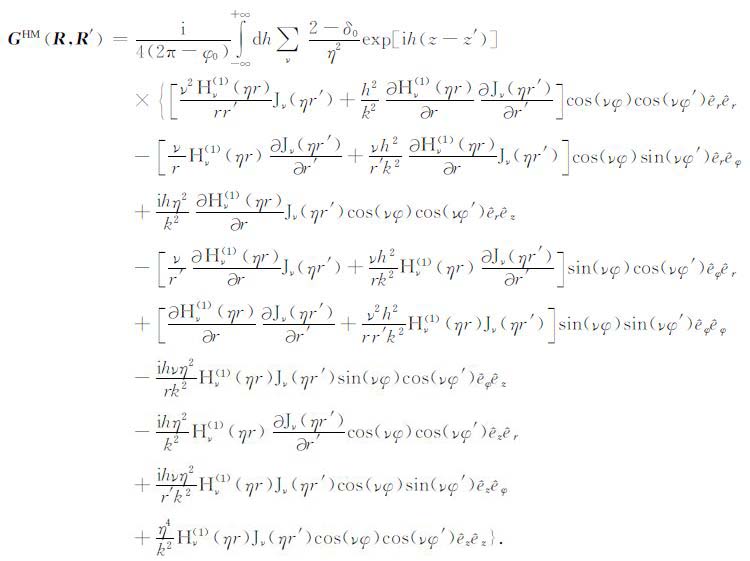
|
(A1) |
当r>r′ 时,式(5)的展开形式为
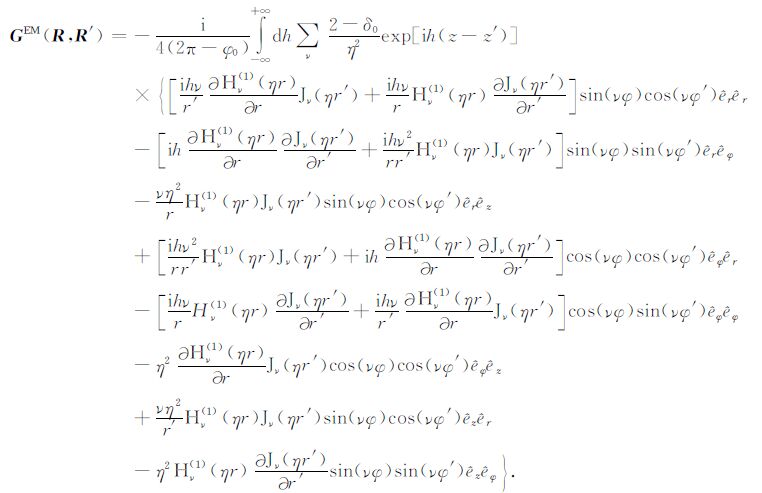
|
(A2) |
对于r<r′ 的情况,只需将式(A1)和(A2)中的H(1)ν (ηr)变为Jν(ηr)、Jν(ηr′)变为H(1)ν (ηr′)即可.
由式(A1)和(A2)可以发现,在边界φ = 0 和φ =2π-φ0 处GHM 和GEM 均满足电磁场的边界条件,即沿任意方向放置的磁流源在理想导体边界φ =0和φ =2π-φ0 处产生的电场强度的切向量($\hat{e}$r、$\hat{e}$z分量)为0而法向量($\hat{e}$φ 分量)不为0、磁场强度的切向量不为0而法向量为0.
| [1] | Allan V, Sinclair P, Prain K, et al. Design, development and field mtroduction of a unique low-frequency (20 kHz) induction resistivity logging-while-drilling tool. SPWLA 45th Annual Logging Symposium,Paper XX,June , 2004. |
| [2] | Sinclair P L. Method and apparatus for directionalmeasurement of subsurface electrical properties. U. S. Patent 6100696 , 2000, 8. |
| [3] | Murphy D P. Advances in MWD and formation evaluation for2004. Worl Oil , 2004, 225(5): 57-62. |
| [4] | 马哲, 李军, 王朝阳, 等. 随钻感应电阻率测井仪器测量原 理与应用. 测井技术 , 2004, 28(2): 155–157. Ma Z, Li J, Wang C Y, et al. Principle of tool resistivity induction MWD and its in-situ application. Well Logging Technology (in Chinese) , 2004, 28(2): 155-157. |
| [5] | 杨锦舟, 朱军, 马哲, 等. 随钻感应测井探测特性及应用研 究. 测井技术 , 2004, 28(6): 543–546. Yang J Z, Zhu J, Ma Z, et al. On investigation characteristics and application of LWD induction logging tool. Well Logging Technology (in Chinese) , 2004, 28(6): 543-546. |
| [6] | 张旭, 魏宝君, 刘坤, 等. 利用积分方程的加速迭代算法 计算随钻电磁波电阻率测量仪器的响应. 地球物理学报 , 2009, 52(9): 2394–2401. Zhang X, Wei B J, Liu K, et al. Computing electromagnetic wave resistivity MWD tool's response using accelerated iteration algorithm for integral equations. Chinese J.Geophys (in Chinese) , 2009, 52(9): 2394-2401. |
| [7] | 孙向阳, 聂在平, 赵延文, 等. 用矢量有限元方法模拟随钻测 井仪在倾斜各向异性地层中的电磁响应. 地球物理学报 , 2008, 51(5): 1600–1607. Sun X Y, Nie Z P, Zhao Y W, et al. The electromagnetic modeling of logging-while-drilling tool in tilted anisotropic formations using vector finite element method. Chinese J. Geophys (in Chinese) , 2008, 51(5): 1600-1607. |
| [8] | 沈金松. 用有限差分法计算各向异性介质中多分量感应测井的响应. 地球物理学进展 , 2004, 19(1): 101–107. Shen J S. Modeling of the multi-component induction log in anisotropic medium by using finite difference method. Progressin Geophysic (in Chinese) , 2004, 19(1): 101-107. |
| [9] | Millard X, Liu Q H. Smulation of near-surface detection of objects m layered media by the BCGS-FFT method. IEEE Trans. Geosci RemoLe Sensing , 2004, 42(2): 327-334. DOI:10.1109/TGRS.2003.817799 |
| [10] | Wei B J, Simsek E, Liu Q H. Improved diagonal tensor approximation (DTA) and hybrid DTA/BCGS-FFT method for accurate simulation of 3D inhomogeneous objects in layered media. Waves in Random and Complex Media , 2007, 17(1): 55-66. DOI:10.1080/17455030600924949 |
| [11] | 魏宝君, LIUQ H. 水平层状介质中基于DTA的三维电磁 波逆散射快速模拟算法. 地球物理学报 , 2007, 50(5): 1595–1605. Wei B J, LIU Q H. Fast algorithm for simulating 3-D electromagnetic inverse scattering in horizontally stratified medium via DTA. Chinese J. Geophys (in Chinese) , 2007, 50(5): 1595-1605. |
| [12] | Gao G, Torres-Verdin C, Fang S. Fast 3D modeling of borehole nduction data n dipping and anisotropic formations using a novel approximation technique. SPWLA 44th Annual Logging Symposium , 2003, paper VV. |
| [13] | 陈桂波, 汪宏年, 姚敬金, 等. 用积分方程法模拟各向异性地层 中三维电性异常体的电磁响应. 地球物理学报 , 2009, 52(8): 2174–2181. Chen G B, Wang I N, Yao JJ, et al. Modeling of electromagnetic response of 3-D electrical anomalous body n a layered anisotropic earth using ntegral equations. Chinese J. Gephys (in Chinese) , 2009, 52(8): 2174-2181. |
| [14] | 魏宝君. 一种新型随钻电阻率测井仪器的响应和刻度. 地球 物理学报 , 2007, 50(2): 632–641. Wei B J. Response and calibration of a new logging-while-driling resistivity tool. Chinese J. Geophys (in Chinese) , 2007, 50(2): 632-641. |
| [15] | 戴振铎, 鲁述. 电磁理论中的并矢格林函数. 武汉: 武汉大学出版社, 1996 . Dai Z D, Lu S. Dyadic Green's Functions n Electromagnetic Theory (in Chinese). Wu han: Wu han University Press, 1996 . |
| [16] | 张庚骥. 电法测井(上册). 北京: 石油工业出版社, 1984 . Zhang G J. Electrical Logging Method (First part) (in Chinese). Beijing: Petroleum Industry Press, 1984 . |
| [17] | 汪宏年, 陶宏根, 姚敬金, 等. 用模式匹配算法研究层状各 向异性倾斜地层中多分量感应测井响应. 地球物理学报 , 2008, 51(5): 1591–1599. Wang H N, Tao H G, Yao J J, et al. Study on the response of a multicomponent induction logging tool in deviated and layered anisotropic formations by using numerical mode matching method. Chinese J. Geophys (in Chinese) , 2008, 51(5): 1591-1599. |
| [18] | 魏宝君, 王甜甜, 王颖. 用磁流源并矢Gren函数的递推 矩阵方法计算层状各向异性地层中多分量感应测井响应. 地球物理学报 , 2009, 52(11): 2920–2928. Wei B J, Wang T T, Wang Y. Computing the response ofmulti-component induction logging in layered anisotropic formation by the recursive matrix method for magnetic-current-source dyadic Greenfs function. Chinese J. Geophys (in Chinese) , 2009, 52(11): 2920-2928. |
| [19] | BITTAR M S, IU G. Fixed-Depth of Investigation Log for Multi-Spacing Multi-Frequency LWD Resistivity Tools. U.S. Patent 0059514A1 , 2004, 3. |
 2011, Vol. 54
2011, Vol. 54

