2. 吉林大学地球科学学院,长春 130061
2. College of Earth and Science, Jinlin University, Changchun 130061, China
提高地震勘探资料信噪比是应用地震勘探资料探查油气资源的关键任务之一,而提高信噪比的一个突出环节是压制地震勘探资料中的随机噪声.随着勘探目标地表条件复杂性的增加,如山地、林带、沙漠等,所获得的叠前道集信噪比较低,甚至无法分辨有效信息而作为不合格品,这对去噪提出了更高的要求[1~4].近年来,国内外学者就随机噪声压制做了大量的研究并取得了一定的进展,如支持向量回归,小波变换域随机噪声的衰减,多项式拟合,时空双曲滤波,曲波变换等技术[5~10],上述处理技术原理不同,适应条件不同,但对强随机噪声处理效果均不理想.针对地震记录中的强随机噪声,李月等[11]提出了一种基于混沌振子检测强随机噪声下同相轴算法,该方法利用水平动校正技术可以将反射同相轴转换为伪周期波列,基于非线性振子系统对周期信号敏感而对噪声免疫的特性,检测出极低信噪比地震资料中的同相轴信息,这种方法需要补充提取同相轴的后续处理.
时频峰值滤波(time-frequencypeakfiltering,TFPF)是一种压制非平稳确定性限带信号中高斯白噪声的有效方法,已成功应用于脑电信号增强、跳频信号检测等领域,对强随机噪声表现出很好的压制能力[12].在地震勘探信号处理领域,金雷等[13, 14]采用TFPF方法压制合成地震勘探记录中的随机噪声,信噪比可低至-9dB.林红波等[15, 16]提出时频峰值滤波的时窗长度随时间变化能够在压制噪声的同时更好地保护有效信号.李月等[17]系统地分析了TFPF的时窗长度和窗型对压制随机噪声的影响,并给出了TFPF 时窗长度的选取规则.前期研究表明,时频峰值滤波表现出对叠前、叠后道集中强随机噪声的高效压制能力,且具有较少的滤波约束条件,是一种不需要设计滤波区间的“盲"滤波方法,对低信噪比信号具有较强的适应性.但是,由于地震信号幅度差异较大,且为了防止波形畸变不能对信号的均衡处理,应用TFPF 处理实际勘探资料时在频率调制编码过程中会产生信息丢失现象和尺度变换误差,影响滤波的精度及后续处理.为了更好地将TFPF 应用到地震信号去噪领域,需要进一步改进和完善时频峰值滤波.
2 时频峰值滤波 2.1 时频峰值滤波原理[12]
含噪信号s(t)由非平稳确定性限带信号x(t)和加性高斯白噪声v(t)构成,时频峰值滤波[11, 12]通过信号调制编码和时频平面峰值滤波两个步骤压制随机噪声.频率调制编码将含噪声信号s(t)变为解析信号${z_s}(t) = {e^{j2\pi \mu \int_0^l {s(\lambda )d\lambda } }}$ 的瞬时频率,通过求取解析信号zs(t)的Wigner-Ville分布的峰值频率,估计信号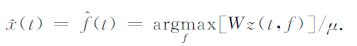
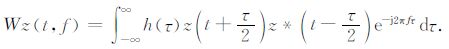
|
(1) |
在窗函数h(τ)内的瞬时频率近似线性,局部线性化的关键因素是时窗长度.在实际应用时,地震信号的频率和噪声强度随时间变化,需要根据信号和噪声的特点选取不同的时窗长度.
2.2 实现时频峰值滤波的误差分析在实际应用时,时频峰值滤波误差主要产生于时频峰值滤波离散化和WVD 的计算上,离散的TFPF在计算WVD时对核函数zs(n+m)zs*(n-m)计算N点的离散傅里叶变换[18, 19]:
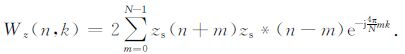
|
(2) |
根据TFPF原理,瞬时频率为Wz(n,k)在时频平面上峰值对应的离散频率kp.将频率kp 转化为模拟频率$\hat{f}$(kp):
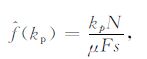
|
(3) |
其中Fs为折叠归一化瞬时频率,N为离散傅里叶变换长度.则频率分辨率为Fs/N.
TFPF的输出是时频平面峰值频率kp 对应的模拟频率$\hat{f}$(kp),与连续信号$\hat{f}$(t)之间存在量化误差,其大小等于瞬时频率的频率分辨率,与傅里叶变换的点数N有关.为了验证TFPF误差与计算傅里叶点数N的关系,取频率25 Hz的正弦信号(图 1a左侧)加入功率为0.3W 的高斯白噪声(图 1a中间)观察N=2i(i=3,4,…,11)的滤波结果(图 1b~d).

|
图 1 谐波信号TFPF离散误差与傅里叶变换点数关系 (a)从左到右分别是谐波信号,含噪谐波信号和不同N值TFPF结果的MSE;(b)〜(d):不同N值TFPF滤波结果. Fig. 1 The relation of discrete error to the number of Fourier Transform (a) Sine signal,noisy sine signal andEMS of filtered sine signal,(b)〜(d) :The filtered sine signal with AS varying from 8 to 2048 |
当N<32 时信号不连续,无法恢复信号;N=64,N=128时,波形基本得到恢复,在波峰、谷处有不平滑现象;N>256后滤波信号基本连续.计算傅里叶变换点数取N不同值时TFPF 输出与真实信号间的均方误差MSE(图 1a右侧),可见N越大,量化误差越小,大于一定值时基本稳定.考虑到运算量随N的增加呈指数规律增加,所以不能无限制的增加N,在实际应用中应权衡计算精度和速度的关系选择合适的N.
N确定之后,还要考虑地震信号幅度剧烈变化和TFPF的尺度变换引起的误差,尺度变换将信号的幅度线性变换到瞬时频率的范围内,即将信号的最大值转换为瞬时频率的最大值(归一化频率,0.5),将信号的最小值转换为瞬时频率的最小值(0).在地震勘探过程中,考虑子波在地下传播的特性及幅度、频率衰减,在一道地震记录中初至波幅度很强,然后随到时增加幅度急剧下降,如图 2a所示,一道记录信号幅值变化范围很大.TFPF 将较大范围数值缩放至瞬时频率范围内时,深层反射的微弱信号变化幅度则更加微小,若直达波幅度与微弱反射波幅度之比超过瞬时频率估计的量级,微小变化无法反映,滤波后的信号波形呈阶梯状波,这将损失许多有效信息.考虑到上述引起误差因素,在处理实际地震记录时应采用分段时频峰值滤波(S-TFPF),即将一道地震记录分作若干段,使得每一段的幅度处于同一数量级,以减小信号幅度剧变带来的误差.

|
图 2 地震信号分段 (a)分段的地震信号;(b)信号的短时能量. Fig. 2 Segmenting seismic signal (a) Segmented seismic signal;(b) Short energy of the seismic signal. |
将一道地震信号分成能量均衡的若干段进行时频峰值滤波处理,即分段时频峰值滤波.该方法将一道长为Ns个采样点的地震信号s(n),n=1,2,…,Ns分成长为L的若干段,第m段信号sm(n)表示为

|
(4) |
其中M为正整数,表示分段数.当L×M大于数据长度Ns时,令第M段信号为剩余数据,sM(n)=s(n),L(M-1)+1≤n≤Ns.则一道信号可以表示为
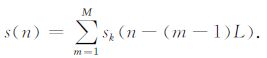
|
(5) |
为了保证一段内的数据能量均衡,使得能量强的初至波不影响能量较弱的信号,从信号初至时刻ti开始分段,数据段长度L通常取初至波持续的时间长度,即信号初至时刻ti到初至波结束时刻te的时间长度,如图 2a所示.
利用地震信号短时能量的剧烈变化确定初至波开始、结束时间及分段长度L.短时能量是语音信号分段的常用方法,定义为
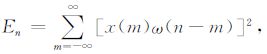
|
(6) |
式中ω(n)为窗函数.图 2b是图 2a中归一化地震信号的短时能量En,它描绘了地震信号能量的变化规律,短时能量突然增加和减少的时刻分别与地震初至波开始和结束的时刻吻合.选取一道参考信号估计初至波能量的范围,设定能量上、下限阈值TH1和TH2,选择En≥TH1 的时刻为初至波开始时刻ti,第一次En≤ TH2 的时刻为初至波结束时刻te,从而确定分段长度L,如图 2b所示,由短时能量确定的初至波开始时刻t′i与结束时刻t′e、ti和te非常接近.
分段时频峰值滤波分别对每一段信号sm(n)进行处理,得到每一段的滤波结果:
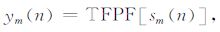
|
(7) |
式中TFPF[·]表示时频峰值滤波操作符.对所有段滤波结果移位求和得到原地震信号滤波的结果
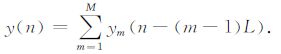
|
(8) |
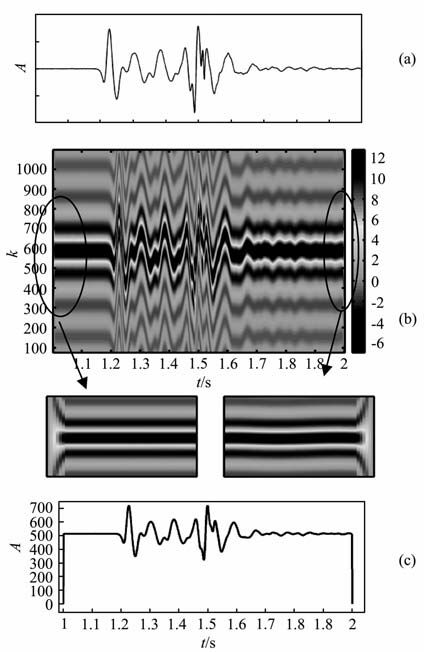
由于采用PWVD 实现时频峰值滤波,在计算数据两端(当前采样点n到数据两端的点数小于窗长)的PWVD 时,由于能够利用的采样点数小于TFPF时窗长度,导致解析信号的PWVD 两端产生端点突变现象,造成时频峰值滤波的结果在两端偏离真实信号.取某道地震记录的1~2s的数据为例(见图 3a),频率调制编码后解析信号的PWVD(图 3b),其能量峰值对应的频率与时域信号波形一致,但是在两端的能量比较平均,没有在解析信号的瞬时频率处聚集(见图 3b放大部分).对解析信号的PWVD 按频率取最大值之后的瞬时频率估计(图 3c)与原信号相比波形一致,在信号两端存在突变.由于各个时刻的瞬时频率估计之间没有影响,所以两端的突变不影响中间的滤波结果.
|
图 3 时频峰值滤波端点畸变 (a)一段地震信号;(b)该段信号的解析信号的PWVD;(c)PWVD的峰值频率. Fig. 3 Endpoint distortion of TFPF (a)A segment of seismic signal;(b)PWVD of analysis signal; (c)The frequency according to peak of PWVD. |
为了避免端点失真,对每段数据两端进行边缘拓展,拓展长度为时频峰值滤波窗长的一半,幅度为端点采样点幅度,即
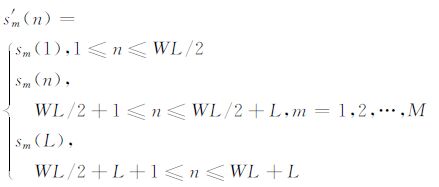
|
(9) |
其中WL为时频峰值滤波时窗长度.对拓展后的数据进行时频峰值滤波处理,滤波结果y′m(n)=TFPF[s′m(n)],然后舍去滤波结果的拓展边缘以抑制端点畸变效应,得到每段的滤波结果:
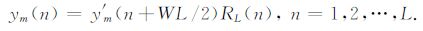
|
(10) |
分段时频峰值滤波处理实际地震资料时,每个数据段信号和噪声的特征不同,因此分段时频峰值滤波的时窗长度应随之改变.
前期研究表明,时窗长度选择与信号的曲率,采样率和噪声强度有关[17]:在相同窗长条件下,曲率越大,引起的均方误差越大;信号采样率越大,窗长越小;噪声方差越大,则窗长越大.地震反射信号在地下传播时受到地下介质的吸收,其频率和幅度衰减具有一定的规律,分段时频峰值滤波各数据段时窗长度应随按此规律变化,对噪声集中的段选择大的窗长提高信号压制效果,对于信号集中部分选择适当的小窗长以减小对有效信号的损失.故分段时频峰值滤波时窗长度分布规律如下:(1)一道地震信号幅度随时间增加而降低,信噪比降低,频率随时间的增加而衰减,时窗长度随时间增加而加大;(2)在空间分布上,随着炮检距的增加,信号的幅度和频率衰减;时窗长度随炮检距的增加而加大.
在实现时频峰值滤波技术时,时窗长度的选择在按上述规律分布的基础上根据各段信号的特征做适度调整.时频峰值滤波的窗长是以当前采样点n为中心[n-WL/2,n+WL/2]范围内的采样点数,一个窗长内信号的非线性通过波形曲率来衡量,在相同时窗条件下,曲率越大,引起均方误差越大[15].TFPF 对地震子波信号波形的影响主要产生于信号的波峰和波谷等曲率较大处,而在波峰和波谷之间的信号滤波后结果基本与原子波吻合.
以主频为10、30 Hz和50 HzRicker子波为例,在一个视周期(波谷之间的时间长度)T=1/fd内,采样数NT=Fs/fd,当采样频率Fs=1000Hz,在波谷之间的采样点数NT为100,33和20个采样点,峰值和波谷间的近似宽度Np=0.25*NT,上述信号的波峰宽度分别是25、9、5个采样点,如图 4所示.在波峰处,10 Hz子波的波峰形状比较平坦,30Hz子波峰内大约5个点,且非线性强,50 Hz子波波峰内约有3个采样点,其波形尖锐.若时窗宽度在波峰处小于波峰宽度,信号幅度压缩到很小的值,瞬时频率可以近似线性;反之,时窗长度大于波峰宽度,时窗内瞬时频率非线性增加,使得滤波信号与真实信号出现偏差.

|
图 4 波峰采样点数 Fig. 4 Number of samples in WL of fd |
综合上述实验结果,考虑到滤波均方误差最大的情况和实际应用中的需要,分段TFPF 各段时窗长度不应大于波峰的采样点数.波峰和波谷处时窗长度WL按如下方法近似选取
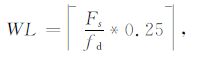
|
(11) |
$\left\lceil \centerdot \right\rceil $表示向上取整操作,当WL为偶数时,WL加1使其变为奇数.
4 算例分析为了验证分段时频峰值滤波的有效性,通过构建仿真模型和实际算例研究分段时频峰值滤波的滤波效果.
4.1 模型仿真利用Ricker子波构建40道地震信号模型,包含4个同相轴,如图 5a所示.Ricker子波的表达式为
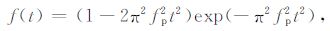
|
(12) |
其中,t表示时间,单位s;fp 表示谱峰频率,单位是Hz;且有fd ≈1.3fp.构建模型的参数如表 1所示.
|
|
表 1 合成地震记录四同相轴参数 Table 1 The parameters of four events in synthetic data |
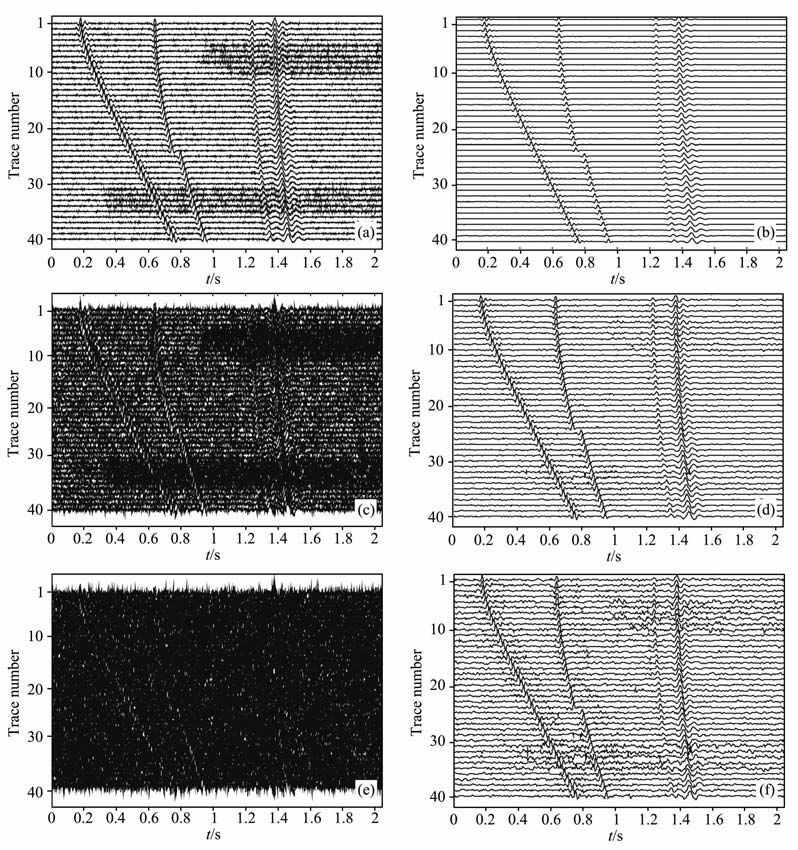
在模型中分别加入噪声强度逐渐增强且随时间变化的高斯白噪声,构建不同信噪比模型数据(如表 2所示),含噪人工合成记录如图 5(a、c、e).由于信号的幅度变化不大,信号频率特征和信噪比随着时间的推移而变化,采用分段时频峰值滤波处理时,主要是依据各道记录信号和噪声分布的区域分段,信号所在段根据信号主频选择相应的时窗长度,以保证每个同相轴所在区域的时窗长度随信号特征变化而不同,噪声所在的段取较长的窗长以有效压制随机噪声.时窗长度是时变的,而各道信号和噪声分布各不相同,因此时窗在空间上也是变化的,如表 3所示.采用时变、空变时窗的分段时频峰值滤波的结果分别显示于图 5(b、d、f).
|
|
表 2 分段时频峰值滤波前后信噪比 Table 2 The SNR of segmenting TFPF |
|
图 5 含噪声合成记录分段变窗长TFPF滤波结果 (a)含噪记录SN只= 10. 7;(b)含噪记录(a)S_TFPF滤波结果;(c)含噪记录SNR=-3.1;(d)含噪记录(c)滤波结果;(e)含噪记录SNR= - 9.2;(f)含噪记录(c)滤波结果. Fig. 5 The filtered results of noisy synthetic data by S-TFPF (a) Noisy synthetic data SNR=10. 7;(b) The filtered results of (a) ; (c) Noisy data SNR=-3. 1; (d) The filtered results of (c) ; (e) Noisy data SNR= -9.2,(f) The filtered results of (e). |
|
|
表 3 分段时频峰值滤波时窗参数 Table 3 The window length parameter of segmenting TFPF |
分析图 5(b、d、f) 可以看出:滤波后勘探记录中强随机噪声被有效压制,在噪声较弱时压制得最好,随着噪声强度的增加,压制随机噪声效果有所下降,但仍能较好地恢复有效同相轴,勘探记录信噪比显著提高(如表 2).由于分段时频峰值滤波不同道的不同时段采用的时窗长度不同,在噪声段采用窗长15,在信号段分别采用窗长7、9和11以适应不同频率特征的反射子波,从而在压制噪声的同时更好地保护有效信号特征.采用窗长为15的S-TFPF 在噪声区间内随机噪声被压制得最好;在时窗长度为7的轴1区域内有效信号得到较好的恢复,而强随机噪声虽然得到压制,但残留也相对较多(图 5f).
4.2 实际算例以某地区共炮点地震勘探记录为例(如图 6 左侧所示)分析分段时频峰值滤波压制噪声和保留信号特征的能力.所选取的地震记录初至信号强度很强,随走时增加记录中信号幅度急剧下降,其信号幅度大约为该道最大幅度的1/100.分别对地震记录直接采用时频峰值滤波(图 6中间)和分段时频峰值滤波处理(每隔0.6s为一段,图 6右侧),与滤波前相比两种方法处理后图像中背景噪声减弱,尤其在矩形框区域,两种方法对强噪声压制效果明显,且有微弱同相轴显露出来.分段时频峰值滤波背景噪声压制得更干净,在压制随机噪声的同时更好地保留了波形特征,椭圆区域的同相轴保持完好.在虚线矩形框区域,TFPF结果出现不连续的阶梯状畸变,这主要是由于信号幅值差异过大引起幅度缩放时微小信号丢失,而分段时频峰值滤波结果波形连续.为了更好地说明这个问题,我们取其中一道记录放大比较(图 7),滤波后的波形与原波形一致,但从图 7b放大区域可见TFPF 滤波后信号存在阶梯状的量化误差,信号幅度不连续,而分段时频峰值滤波结果(图 7c)波形连续,消除了阶梯状畸变.

|
图 6 分段时频峰值滤波结果比较 左侧滤波前信号,中间为TFPF结果,右侧为分段时频峰值波结果. Fig. 6 The comparision whti TFPF and Segmenting TFPF(S-TFPF) Left part:a trace of seismic data; middle part: the Iliteded signal by TFPF and right part : the filtered signal |

|
图 7 分度时频峰值滤波结果比较 (a)滤波前信号;(b) TFPF结果;(C)分段时频峰值波结果. Fig. 7 The comparision with TFPF and Segmenting TFPF(S-TFPF) (a) A trace of seismic data; (b) The Iliteded signal by TFPF; (c) The filtered signal by S-TFPF. |
分段时频峰值滤波处理地震记录结果表明,分段时频峰值滤波技术对于低信噪比地震资料中随机噪声压制效果明显,采用时变、空变时窗参数滤波在波形上没有明显的畸变,能够显著改善勘探记录的信噪比.共炮点勘探记录(图 6)矩形框区域内的随机噪声较强,经分段时频峰值滤波处理后噪声得到抑制,且与噪声较弱段的随机噪声压制效果基本一致;从有效信号上看,滤波后的记录中同相轴没有畸变和衰减现象.在椭圆区域内,由于随机噪声被有效抑制,同相轴的连续性得到改善,能更有效地识别同相轴.
综上所述,分段时频峰值滤波方法采用短时能量对地震信号分段,可以使每一段信号幅度均衡,分段时频峰值滤波方法有效改善了一般时频峰值滤波结果中的阶梯状误差;对每段信号端点拓展,有效地去除各段端点失真.并结合实际地震资料信号的频率、噪声强度变化规律,根据各段信号子波的非线性特征调整各段信号的时窗长度;对于噪声强度较大的段,适当选择较大的时窗长度以压制地震勘探随机噪声,对于信号段选择与子波匹配的窗长,能够在有效压制随机噪声的同时良好地恢复有效地震信号.与一般时频峰值滤波相比,分段时频峰值滤波解决了TFPF处理实际资料时的实际问题,为地震勘探信号处理提供更精确的随机噪声压制方法.关于信号段和噪声段的判别方法有待进一步研究.
| [1] | Zang Z J, Klemperer S L. West-east variation in crustal thickness in northern Lhasa block central Tibet, from deep seismic sounding data. Journal of Geophysical Research , 2005, 110: B0943. |
| [2] | Zhang Z J, Wang G J, Harris J M. Multi-component wavefield simulation in viscous extensively dilatancy anisotropic media. Phys. Earth Planet Inter. , 1999, 114: 25-28. DOI:10.1016/S0031-9201(99)00043-6 |
| [3] | 樊德华, 段云卿, 张婉, 等. 三维地震勘探抽油机噪声特征分析. 石油地球物理勘探 , 2008, 43(6): 662–667. Fan D H, Duan Y Q, Zhang W, et al. Analysis on noise feature of pumping unit in 3-D seismic exploration. Oil Geophysical Prospecting (in Chinese) , 2008, 43(6): 662-667. |
| [4] | 勾丽敏, 蔡希玲, 刘学伟, 等. 噪声对叠前深度偏移层速度精度的影响分析. 石油地球物理勘探 , 2007, 42(2): 156–162. Gou L M, Cai X L, Liu X W, et al. Influence analysis of noise on precision of prestack depth migration interval velocity. Oil Geophysical Prospecting (in Chinese) , 2007, 42(2): 156-162. |
| [5] | Deng X Y, Yang D H, Peng J M, et al. Noise reduction and drift removal using least-squares support vector regression with the implicit bias term. Geophysics , 2010, 75(6): 119-127. |
| [6] | 高静怀, 毛剑, 满蔚仕, 等. 叠前地震资料噪声衰减的小波域方法研究. 地球物理学报 , 2006, 49(4): 1155–1163. Gao J H, Mao J, Man W S, et al. On the denoisingmethod of prestack seismic data inwavelet domain. Chinese J. Geophys. (in Chinese) , 2006, 49(4): 1155-1163. |
| [7] | 张军华, 吕宁, 田连玉, 等. 地震资料去噪方法技术综合评述. 地球物理学进展 , 2006, 21(2): 546–553. Zhang J H, Lu N, Tian L Y, et al. An overviews of the methods and techniques for seismic data noise attenuation. Progress in Geophysics (in Chinese) , 2006, 21(2): 546-553. |
| [8] | 李月, 杨宝俊, 林红波, 等. 地震勘探时空域双曲滤波因子的特点与提高信噪比的能力. 地球物理学报 , 2008, 51(5): 1557–1566. Li Y, Yang B J, Lin H B, et al. Characteristics of hyperbolic time-distance relation filter in seismic prospecting and its ability increasing signal-to0noise ratio. Chinese J. Geophys. (in Chinese) , 2008, 51(5): 1557-1566. |
| [9] | Ramesh Neelamani, Anatoly I. Baumstein and Dominique G. Gillard. Coherent and random noise attenuation using the curvelet transform. The Leading Edge , 2008, 27(2): 240-248. DOI:10.1190/1.2840373 |
| [10] | 陈雨红, 杨长春, 曹齐放, 等. 几种时频分析方法比较. 地球物理学进展 , 2006, 21(4): 1180–1185. Chen Y H, Yang C C, Cao Q F, et al. The comparison of some time-frequency analysis methods. Progress in Geophysics (in Chinese) , 2006, 21(4): 1180-1185. |
| [11] | 李月, 杨宝俊, 赵雪平, 等. 检测地震勘探微弱同相轴的混沌振子算法. 地球物理学报 , 2005, 48(6): 1428–1433. Li Y, Yang B J, Zhao X P, et al. An algorithm of chaotic vibrator to detect weak events in seismic prospecting records. Chinese J. Geophys. ( in Chinese) (in Chinese) , 2005, 48(6): 1428-1433. |
| [12] | Boashash B, Mesbah M. Signal enhancement by time- frequency peak Filtering. IEEE Trans. Signal Processing , 2004, 52(4): 929-937. DOI:10.1109/TSP.2004.823510 |
| [13] | 金雷, 李月, 杨宝俊. 用时频峰值滤波方法消减地震勘探资料中随机噪声的初步研究. 地球物理学进展 , 2005, 20(3): 724–728. Jin L, Li Y, Yang B J. Reduction of random noise for seismic data by time-frequency peak filtering. Progress in Geophysics (in Chinese) , 2005, 20(3): 724-728. |
| [14] | 林红波, 李月, 潘伟. 时频峰值滤波信号增强方法在实际地震资料处理中的应用. 吉林大学学报(地球科学版) , 2007, 37(5): 1038–1041. Lin H B, Li Y, Pan W. Application of signal enhancement method based on time-frequency peak filtering to seismic data processing. Journal of Jilin University (Earth Science Edition) (in Chinese) , 2007, 37(5): 1038-1041. |
| [15] | Lin Hongbo, Li Yue, Yang Baojun. Recovery of Seismic Events by Time-Frequency Peak Filtering. IEEE ICIP 2007 : v-441-v-444. |
| [16] | 林红波, 李月, 叶文海, 等. 时频峰值滤波去噪技术及其应用. 地球物理学进展 , 2008, 23(6): 1953–1957. Lin H B, Li Y, Ye W H, et al. Denoising technique based on time-frequency peak filtering and its application. Progress in Geophysics (in Chinese) , 2008, 23(6): 1953-1957. |
| [17] | 李月, 林红波, 杨宝俊, 等. 强随机噪声条件下时窗类型局部线性化对TFPF技术的影响. 地球物理学报 , 2009, 52(7): 1899–1906. Li Y, Lin H B, Yang B J, et al. The influence of limited linearization of time window on TFPF under the strong noise background. Chinese J. Geophys. (in Chinese) , 2009, 52(7): 1899-1906. |
| [18] | Nelson D J, Smith D C. Adaptive interference removal based on concentration of the STFT. Digital Signal Processing , 2006, 16(5): 597-606. DOI:10.1016/j.dsp.2005.03.004 |
| [19] | Cohen L. Time Frequency Analysis. Englewood Cliffs:Prentice Hall , 1995. |
 2011, Vol. 54
2011, Vol. 54



