一直以来研究横向非均匀介质的波场外推是反射地震勘探学的重点[1],这包括速度反演、叠前偏移、陡倾角偏移等,通常采用的方法为频率波数域法、Kirchhoff积分法、有限差分法、有限元法等[2].
而在众多的偏移方法当中,成熟的有限差分波动方程偏移技术则以其高效、低噪、适应能力强等优点而备受关注[3~8].为了保留有限差分偏移技术的上述优点,同时解决传统有限差分偏移方法的倾角限制,国内外学者做了大量的研究,马在田[9]采用阶数分裂的方法,将高阶方程分解为二、三阶近似式来解决倾角限制;Stolt[10]则在15°偏移方程的基础上,用傅里叶变换继续沿深度方向求导,略去波场沿深度的三阶偏导得45°偏移方程;王尚旭等[11]、底青云等[12]采用有限单元法,避免了近似差分方程带来的误差,解决各向异性介质中倾角反射偏移问题;李广场[13]用线性坐标变换的方法,对标量波动方程进行一系列精确变换,得到了均匀介质下的探地雷达(GPR)波场外推差分方程,实现了均匀介质条件下的GPR 全倾角偏移.本文在前人研究的基础上,对均匀介质中的线性变换差分偏移算法进行改进,推导了横向非均匀介质中的线性变换差分偏移方程,并编制了相应的GPR 偏移程序[14, 15],结合输入的初始速度矩阵值,来提高复杂非均匀变速介质中GPR 剖面的偏移精度.
2 均匀介质中的线性变换差分偏移算法 2.1 线性变换概念对二维弹性模型,探地雷达高频电磁波近似服从双程标量波动方程:
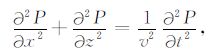
|
(1) |
式中P为雷达波场值,v为雷达波速.
类比于15°偏移方程中的浮动坐标变换,设存在另一种变换,使方程(1)写成如下普遍形式:
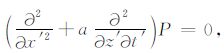
|
(2) |
系数a由波速决定,令线性变换:
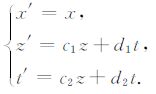
|
(3) |
在均匀介质中,c1,c2,d1,d2 为常数,变换(3)式的物理意义是通过将原坐标系下的时空参量进行线性组合来代替新坐标系下的时空参量,最终改变波场的延拓方向,将其代入到方程(1)中,即:
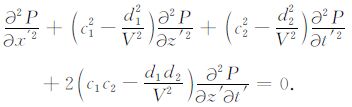
|
(4) |
令(4)式与(3)式相等即求得特殊变换:
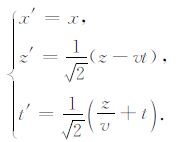
|
(5) |
代入原标量波动方程,得到同15°偏移方程形式相同的精确方程:
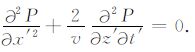
|
(6) |
方程(6)未作任何近似,它是在均匀介质条件下标量波动方程的精确变换,该方程也是均匀介质线性变换波动方程的定义表达式,应用该式进行波场外推没有任何倾角限制.
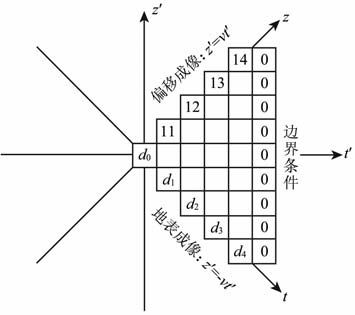
2.2 线性变换的差分格式常规偏移算法以P(x,z= 0,t)为雷达地表数据,P(x,z,t=0)为偏移后的雷达剖面,上行波边界条件为P(x,z,t) (t+z/v)>Tmax =0,而在线性变换后的新坐标系(x′,z′,t′)中,P(x′ =x,z′ =-vt/$\sqrt{2}$,t′ =t/$\sqrt{2}$)则为雷达地表数据,P(x′ =x,z′ =z/$\sqrt{2}$,t′ =z/(v$\sqrt{2}$))为偏移剖面,P(x′,z′,t>T/$\sqrt{2}$)=0为边界条件,在(z′,t′)平面上,线性变换差分格式如图 1所示,其中x′ 轴垂直于(z′,t′)平面,即雷达波场向量沿x′ 轴分布.
|
图 1 线性变换差分偏移示意图 Fig. 1 Sketch map of the linear transformation of the finite difference migration method |
在新的坐标系(x′,z′,t′)下,差分网格如图 1所示,地表数据可从平面z′ =-vt′ 上得到,根据ERM 成像原理,在(z′,t′)平面中,在边界条件约束下,波场延拓可向上或向左进行,将平面-vt′ 上的数据从t轴向z轴外推,通过循环求解三对角矩阵所对应的线性方程组,最终求得平面vt′ 上的数据并输出,考虑到方程求解的数值稳定性,采用隐式Crank-Nicolson差分格式,方程(6)的有限差分格式为

|
(7) |
其中,a=VΔt′Δz′/(8Δx′2),I是以(0,1,0)为主对角元素的三对角矩阵,T是以(-1,2,-1)为主对角元素的三对角矩阵,可加进x′ 写成单元格形式:
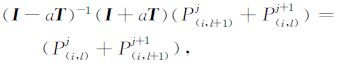
|
(8) |
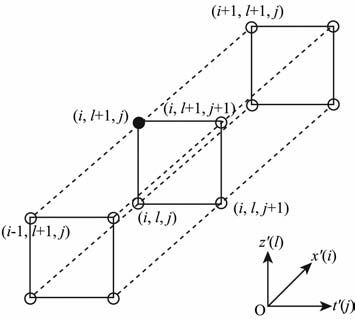
左侧第一项P(i,l+1)j为网格j时间、l+1深度处沿x′分布的雷达波场矢量值,该项可隐式地由方程右边三个已知向量的元素Pj(i,l),Pj+1(i,l),Pj+1(i,l+1)给出,由方程(8)知,与15°有限差分的五点差分格式不同,经线性变换的差分格式为四点差分格式,如图 2、图 3所示.

|
图 2 (x,z,t)中的五点差分格式 Fig. 2 Five-point difference format in(x,z,t) |
|
图 3 (x′,z′,t′)中的四点差分格式 Fig. 3 Four-point difference format in (x′,z′,t′) |
对方程(8)进一步改写为:
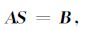
|
(9) |
未知量S的分量Si= (P(i,l+1)j,l)),已知量B的分量Bi= (P(i,l)j+P(i,l+1)j+1),系数矩阵
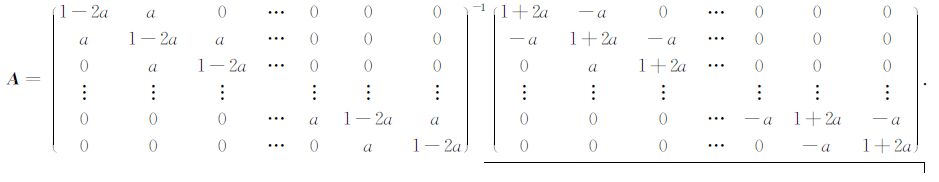
|
在Matlab程序进行迭代初始,即置l=0,j=T时,P(i,0)T-1可由地表数据得知,P(i,0)T,PT(i,1)为零,设置j为外循环,l为内循环,在每一时间层j和深度层l上时,循环求解该大型三对角线性方程组时调用M文件中定义的快速追赶法[16~18]函数.
3 非均匀介质中线性变换差分偏移算法在非均匀介质情况下,引入速度参数V(x,z),即雷达波速为横纵向坐标的函数,将其代入到二维标量波动方程中:
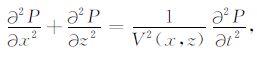
|
(10) |
定义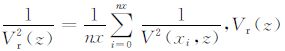
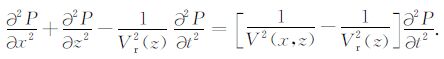
|
(11) |
与传统有限差分偏移算法相类似,用时间的概念来代表深度,定义

|
(12) |
类似地,再进行线性变换:
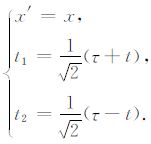
|
(13) |
线性变换(13)式同样是通过对(x,τ,t)坐标系中时空参数进行线性组合来改变雷达波场的延拓方向,代入方程(12)则变为:
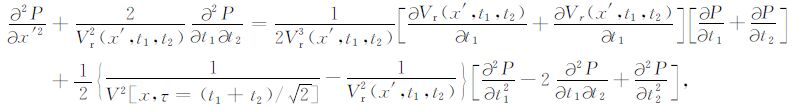
|
(14) |
其中Vr(x′,t1,t2)=Vr[x′,τ= (t1+t2)/$\sqrt{2}$],这样在新的坐标系(x′,t1,t2)中,方程(14)为非均匀介质中线性变换差分偏移表达式,文章研究了右端第一项对最终的雷达偏移剖面带来的影响,暂且将其称为混合因子项,该混合因子项在处理横向非均匀介质问题时具有重要作用.当利用方程(14)进行波场外推时,正是由于该混合因子项的存在,当外推至横向非均匀的速度突变处时,会产生强烈的反射.故对复杂GPR 剖面进行偏移处理时,我们可根据偏移的主要目的,灵活地选择是否加入混合因子项.如,当我们对模型中横向介质速度变化平缓的主要反射体感兴趣时,考虑到输入速度值为标量,同时要减弱精细异常体因强烈反射引起的干扰,通常选择省略该混合因子项;相应地,如需对复杂介质中的多次反射质点准确归位时,由于横向介质速度变化剧烈,并考虑到输入速度值为矢量矩阵,可加入混合因子项,它能对横向速度突变处的多次反射质点归位更准确,获得的雷达偏移剖面分辨率更高.
4 速度估计应用改进型线性变换差分偏移程序进行波场外推时,需输入速度矩阵,在实际操作中则是根据偏移处理后图像的成像效果,对速度矩阵进行不断修正,这样逐渐逼近地下介质的真实速度参数,所以准确的初始速度参数是该偏移算法的关键.本文采用了刚性边界反射系数估计法[19, 20],通过观测地下浅层介质和铁板的反射信号,分别得到各自对应的反射波振幅,根据不同介质振幅求得雷达波速:

|
(15) |
式中As、Am 分别为浅层介质和铁板反射波振幅,c为电磁波在空气中的传播速度,可以求取雷达剖面100道数据振幅的平均值As、Am.
在实际波速估计中,将探测区域的岩芯来代替铁板,即先求取岩芯的反射系数,其步骤为:
(1) 取雷达探测区域的岩芯,在实验室测定其介电常数,并计算其传播速度V0;
(2) 由式(15)求得岩芯的反射系数:
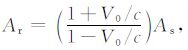
|
(16) |
(3) 取雷达测区内记录的100道波形,求取对应相位在地表的振幅值;
(4) 在测线不同位置上,应用(15)式,其中Ar代替了Am:

|
(17) |
式中Ai 为地表某位置i处的雷达波反射振幅值,Ar为步骤(2)中求得的该介质的反射系数,这样在横向不同的位置上能够得到较精确的初始速度矩阵值,将该速度矩阵输入到程序中运行即可.
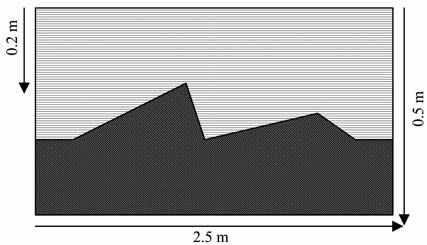
5 偏移实例 5.1 不同倾角的锲形地电模型首先验证算法在均匀介质中解决倾角限制的有效性,选择一个锲形模型,如图 4 所示.该模型为2.5m×0.5m 矩形空间,上层为粘土层,下层为湿砂层,介质的电导率σ1 =1.4×104 S/m,σ2 =0.0069S/m,介质的相对介电常数ε1=2.6,ε2=25,取天线中心频率为900 MHz,模型中设置了30°、75°、15°三种倾角的反射界面.
|
图 4 不同倾角的锲形地电模型 Fig. 4 Wedge of homogeneous geoelectric model with different angle |
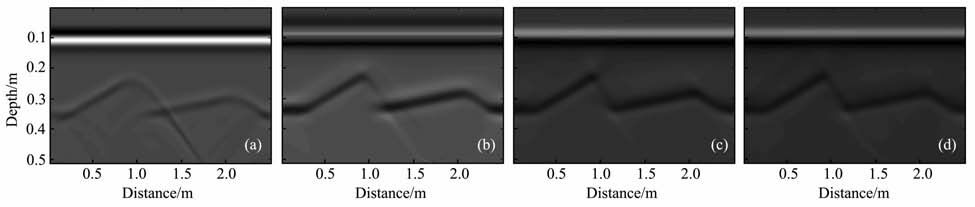
图 5a为该模型的正演模拟结果,只能看出锲形界面的波浪形态,正演结果比较模糊,尤其是陡倾角一侧,基本无法辨明其轮廓,由于绕射波的存在,在不同倾角的界面交界处产生强烈的“绕射尾巴",并一直延伸至矩形框底部,见图 5a中的波谷处.
|
图 5 不同倾角的锲形地电模型用不同偏移算法处理的结果 (a)正演模拟结果;(b) 15°有限差分偏移结果;(c) 45°有限差分偏移结果;(d)线性变换差分偏移结果. Fig. 5 The migrated GPR results of wedge with ditferent angle using different migration method (a)The forward modeling results;b)The results of finite difference migration with the 15-degree operator;c)The results of finite difference migration with the 45-degree operator ;d)The results of linear transformation of finite difference migration. |
为了对比各种算法的偏移效果,首先采用15°有限差分偏移算法对其进行处理,结果如图 5b 所示,可以看出,15°和30°倾角界面的轮廓已经基本清晰,顶点位置恢复了模型中的深度,只是75°倾角界面不能顺利归位成像,这表明15°算法对陡倾角反射界面偏移的处理能力不够.图 5c为45°偏移算法处理的结果,与前者相比,无论是成像质量、倾角归位还是绕射波收敛能力,45°算法处理的效果更理想,75°倾角界面能辨明其基本轮廓,只是在顶点处产生了绕射,总体来说45°算法在15°算法基础上有了很大的提高,图 5d为线性变换有限差分偏移算法处理的结果,各倾角的界面都得到了很好的归位,界面交界处的“绕射尾巴"已经完全收敛,75°倾角界面轮廓清晰可见,两个顶点的位置恢复了模型中的深度,对陡倾角反射界面偏移处理的整体效果比较理想.
5.2 实测雷达资料为验证改进型线性变换差分偏移算法处理横向非均匀介质的有效性,作者选取了某隧道左边墙K76+150-K76+156段初期支护雷达实测剖面,实际探测任务为检测初期支护与围岩之间是否存在空洞及松散区,为达到探测精度,采用中心频率为1000 MHz屏蔽天线,设置采样间隔为0.15ns,采集时窗为15ns,道间距为0.01m,每道扫描采样点数设为512,有效检测深度为0.8m.
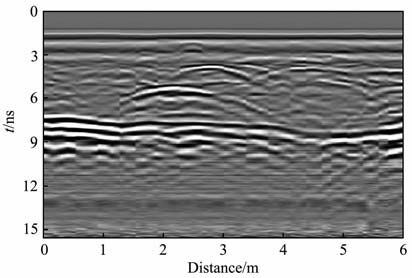
由图 6知,该段存在两处较明显的异常,其中剖面的上部为两个绕射圆弧,下部为倾斜的反射界面,这样上部的绕射圆弧可看作多次反射质点,下部的倾斜反射界面则为主体反射层.
|
图 6 隧道左边墙探地雷达检测剖面图 Fig. 6 The real GPR section of left-sidewall in tunnel |
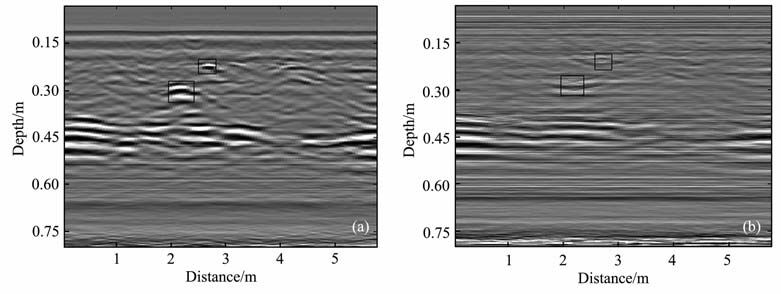
图 7a、7b为未作波速估计时利用改进型线性变换差分偏移算法处理后的剖面,比较带混合因子项和不带混合因子项的处理结果看出,改进的带混合因子项的算法在速度异常变化的质点处产生了强烈的反射波,而略去混合因子项的算法在该处则比较平滑,同时从图 7a反应的剖面可以看出倾斜的界面非连续,其间存在非密实区,可以推断为空洞区,经施工方重新回填灌浆后空洞区已经填实,上部的两绕射双曲线收敛为两质点,经证实分别为塑料排水管和距离拱底2.5m 的边墙锚杆.
|
图 7 用线性变换差分偏移算法处理后的探地雷达实测剖面结果 (a)线性变换差分偏移结果(带混合项);(b)线性变换差分偏移结果(不带混合项). Fig. 7 Migrated GPR section using the linear transformed finite difference method (a) With the mixed factor term added; (b) Without the mixed factor term added. |
基于以上处理结果,利用刚性边界系数法对输入的速度矩阵值进行估计,在隧道支洞K76+200处的开挖岩溶处取岩芯,采用美国BI-870介电常数测定仪测试该岩芯介电常数ε=7.5及电磁波速度V0=0.109 (m/ns),鉴于K76+150-K76+156段的实测雷达剖面数据中包括345 道数据,每道数据包括512个样本,取该段全部的345道波形数据,分别求取该345道波形各自在边墙上对应相位的振幅值,并求出其均值As,由式(16)求出该岩芯所代表的介质反射系数Ar,利用式(17)计算出的各道对应的速度.
将生成的速度矢量矩阵进行输入,再用改进型偏移算法对其进行处理,结果如图 8所示.
|
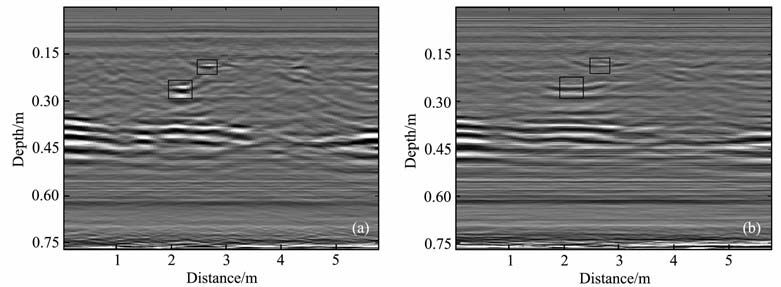
图 8 速度估计后用线性变换差分偏移算法处理后的探地雷达实测剖面结果 (a)含速度估计的算法偏移结果(带混合项);(b)含速度估计的算法偏移结果(不带混合项) Fig. 8 Migrated GPR section using the linear transformed finite difference method based on velocity estimation (a) With the mixed factor term added; (b)Without the mixed factor term added. |
由图 8a可以看出,对输入的速度矩阵进行较精确估计,用带混合因子项的算法偏移后,图像中的空洞区、排水管、边墙锚杆收敛程度更好,与未加入速度估计步骤的算法相比,后者对目标定位的准确度更高,优化了前面的偏移效果,与图 8b相比也可以明显地看出混合因子项的重要作用.
6 结 语传统线性变换有限差分偏移算法实现了均匀介质中全倾角偏移,在此基础上,讨论该算法在横向非均匀介质中的运行情况,推导出改进型线性变换差分偏移方程,解决了原算法对速度的高敏感性,并结合速度估计,提高了探地雷达剖面的偏移精度,成果如下:
(1) 针对加入了速度参数的非均匀介质下探地雷达波动方程,引入线性变换,导出加入了混合因子项的改进型线性变换GPR 逆时偏移算法,给出了算法步骤、编制了相应的Matlab偏移程序.
(2) 应用改进型线性变换GPR 逆时偏移程序分别对复杂的非均匀变速介质地电模型的正演剖面和实测剖面进行了偏移处理,解决倾角限制的同时,该算法可以根据不同的勘探目的,通过选择混合因子项的取舍,来处理介质中同时存在主体反射体和多次反射质点的地质问题,较好地解决了线性变换偏移算法的速度高敏感性问题.并把该算法同15°及45°差分算法偏移算法进行对比,验证了该偏移算法在处理不同地质问题时具有更好灵活性、更高的精确度.
(3) 提出了一种较精确的波速估计优化方法,对非均匀变速介质中线性变换差分逆时偏移速度矩阵参数进行优化,并对实测剖面进行了处理,通过与未经速度估计的偏移算法相比,表明优化后的算法在处理复杂地质模型时,提高了改进型线性变换差分偏移算法对目标体的偏移精度:当以多次反射质点为勘探目的时,优化算法对质点的偏移精度更高,而当以主要反射层为勘探重点时,优化算法对主要反射层的归位更为准确.
| [1] | Li Zhiming. Wave field extrapolation by the linearly transformed wave equation operator. Geophysics , 1986, 51(8): 1538-1551. DOI:10.1190/1.1442204 |
| [2] | 贺振华, 王才经, 李建朝. 反射地震资料偏移处理与反演方法. 重庆: 重庆大学出版社, 1989 . He Z H, Wang C J, Li J C. Reflection Seismic Data Migration Processing and Inversion Method (in Chinese). Chongqing: Chongqing University Press, 1989 . |
| [3] | 冯德山, 戴前伟, 何继善. 探地雷达的正演模拟及有限差分波动方程偏移处理. 中南大学学报(自然科学版) , 2006, 37(2): 361–365. Feng D S, Dai Q W, He J S. Forward simulation of ground penetrating radar and its finite difference method wave equation migration processing. Journal of Central South University (Science and Technology) (in Chinese) , 2006, 37(2): 361-365. |
| [4] | 刘喜武, 刘洪. 波动方程地震偏移成像方法的现状与进展. 地球物理学进展 , 2002, 17(4): 582–591. Liu X W, Liu H. Status and progress on wave equation migration methods. Progress in Geophysics (in Chinese) , 2002, 17(4): 582-591. |
| [5] | 马在田. 地震成像技术有限差分法偏移. 北京: 石油工业出版社, 1989 . Ma Z T. Finite Difference Method Migration of Seismic Image Technique (in Chinese). Beijing: Petroleum Industry Press, 1989 . |
| [6] | 王长清, 祝西里. 电磁场计算中的时域有限差分法. 北京: 北京大学出版社, 1994 . Wang C Q Zhu X L. Time Domain Finite Difference Method in Electromagnetic Field Calculation (in Chinese). Beijing: Peking University Press, 1994 . |
| [7] | 王红落, 常旭, 陈传仁. 基于波动方程有限差分算法的接收函数正演与偏移. 地球物理学报 , 2005, 48(2): 415–422. Wang H L, Chang X, Chen C R. Receiver function forward modeling and migration based on wave-equation finite difference method. Chinese J. Geophys (in Chinese) , 2005, 48(2): 415-422. |
| [8] | 王华忠, 冯波, 任浩然. 二维Offset平面波有限差分法叠前时间偏移. 石油物探 , 2009, 48(1): 11–19. Wang H Z, Feng B, Ren H R. Finite difference pre-stack time migration of 2D offset plane wave. Geophysical Prospecting for Petroleum (in Chinese) , 2009, 48(1): 11-19. |
| [9] | 马在田. 高阶方程偏移的分裂算法. 地球物理学报 , 1983, 26(4): 377–388. Ma Z T. High order equation migration of splitting algorithm. Chinese J. Geophys (in Chinese) , 1983, 26(4): 377-388. |
| [10] | Stolt R H. Migration by Fourier transforms. Geophysics , 1978, 43(1): 23-48. DOI:10.1190/1.1440826 |
| [11] | 王尚旭, 牟永光. 有限元素法全倾角波动方程偏移. 地球物理学报 , 1989, 32(3): 308–318. Wang S X, Mou G Y. Full wave equation dip migration using finite element method. Chinese J. Geophys. (in Chinese) , 1989, 32(3): 308-318. |
| [12] | 底青云, 许琨, 王妙月. 衰减雷达波有限元偏移. 地球物理学报 , 2000, 43(2): 257–263. Di Q Y, Xu K, Wang M Y. The attenuated radar wave migration with finite element method. Chinese J. Geophys (in Chinese) , 2000, 43(2): 257-263. |
| [13] | 李广场. 有限差分法探地雷达波动方程偏移.南京:河海大学土木学院, 2004 Li G C. The wave equation migration of ground penetrating radar by the method of finite difference. Nanjing: College of Civil Engineering, Hohai University, 2004 |
| [14] | Chapman S J. MATLAB Programming for Engineers(Second Edition). Beijing: Science Press, 2002 . |
| [15] | James Irving, Rosemary Knight. Numerical modeling of ground-penetrating radar in 2-D using matlab. Computers Geosciences , 2006(32): 1246-1258. |
| [16] | 刘晓, 李文强. 追赶法在求解循环和拟循环三对角方程组中的一种推广. 河南师范大学学报(自然科学版) , 2009, 37(1): 13–16. Liu X, Li W Q. An extension of chasing method for solving circular and quasi-circular tri-diagonal systems. Journal of Henan Normal University (Natural Science) (in Chinese) , 2009, 37(1): 13-16. |
| [17] | 高德荫, 徐峰, 潘乃德. 一类特殊三对角线性方程组的快速近似追赶法. 计算数学 , 1981(1): 10–17. Gao D Y, Xu F, Pan N D. A special class of tri-diagonal linear equations using fast approximation chasing method. Computational Mathematics (in Chinese) , 1981(1): 10-17. |
| [18] | 李青, 王能超. 解循环三对角线性方程组的追赶法. 小型微型计算机系统 , 2002, 23(11): 1393–1395. Li Q, Wang N C. An algorithm for solving circular tri-diagonal systems. Mini-micro Systems (in Chinese) , 2002, 23(11): 1393-1395. |
| [19] | 于景兰, 王春和. 探地雷达探测地下目标时的波速估计. 地球物理学进展 , 2003, 18(3): 477–480. Yu J L, Wang C H. Estimation of EM wave velocity in detecting underground target by GPR. Progress in Geophysics (in Chinese) , 2003, 18(3): 477-480. |
| [20] | 胡进峰, 周正欧, 罗仁泽. 一种前视探地雷达波速估计方法. 电子学报 , 2007, 35(6): 1113–1117. Hu J F, Zhou Z O, Luo R Z. Research on forward-looking ground penetrating radar velocity estimation. Acta Electronica Sinica (in Chinese) , 2007, 35(6): 1113-1117. |
 2011, Vol. 54
2011, Vol. 54

