2. 中国石油大学中国石油天然气集团公司物探重点实验室,北京 102249;
3. 中海石油(中国)有限公司天津分公司勘探开发研究院,天津 300452;
4. 中国石油化工集团公司胜利油田分公司物探研究院,东营 257022
2. CNPC Key Laboratory of Geophysical Exploration, China University of petroleum(Beijing), Beijing 102249, China;
3. CNOOC Ltd-TianJin Bohai Oilfield E&P Research Institute, Tianjin 300452, China;
4. Geophysical Research Institute of Shengli Oilfield Branch CO., SINOPEC, Dongying 257022, China
偏移速度分析是在分析道集上进行的,道集的提取是偏移速度分析的关键问题,没有假象的速度分析道集是偏移速度分析的良好基础.共成像点道集的传统提取方法在多路径情况下不满足发射率条件[1~3],因而存在假象.由于角度域共成像点道集(ADCIGs)在多路径情况下不会产生假象,因而受到地球物理界的广泛关注.Prucha等[4]首先提出利用双平方根方程偏移的方法得到偏移距射线参数域共成像点道集(PhCIG).Xie等[5]通过小波束分解波场的方法得到角度域共成像点道集.Sava等[6, 7]提出了通过Fourier域径向道变换计算角度域共成像点道集,实现了在偏移后提取角度域共成像点道集的方法,大大减少了角度域共成像点道集的计算时间.陈生昌等[8]利用波场外推的单平方根算子和波场的窗口Fourier框架展开与重构,提出一种构建局部角度域共成像道集方法.Sava和Fomel[9]提出了抽取转换横波伪角度域共成像点道集的方法.Rosales等[10, 11]采用波动方程方法对转换波角度域共成像点道集的提取展开了研究,其不足之处在于需要事先求得地层的倾角,而倾角的计算误差势必会影响转换波角度域共成像点道集的提取精度.
在对角度域共成像点道集研究的同时,基于角度域共成像点道集的偏移速度分析方法也在逐步发展.Biondi和Symes[12]分析了在当前速度误差下的角度域共成像点道集的运动学性质,并推导了角度域共成像点道集的剩余时差方程.Biondi和Tisserant[13]将这一研究扩展到3D 情况.Sava和Biondi[14, 15]基于角度域共成像点道集道集拉平原则和最大聚焦原则,利用波场延拓方法进行了波动方程偏移速度分析,该方法应用线性波动方程算子将成像扰动与偏移速度扰动联系起来进行速度的更新.Xia等[16]在共角度域成像的框架下将构造倾角与剩余偏移速度分析结合在深度-偏移距射线参数域建立了剩余偏移速度分析方程.刘守伟等[17]提出了利用时空移动成像条件抽取纵波时移角度域共成像点道集的方法,并在此道集上对纵波速度进行了更新.Zhang等[18]建立了在角度域进行剩余曲率速度分析的方法.
当前角度域共成像点道集偏移速度分析方法大都是针对纵波开展的研究,对于转换波偏移速度分析,尤其是弹性波偏移速度分析方法的研究鲜有报道.考虑到基于波动方程的角度域共成像点道集的提取方法精度固然很高,但计算效率比较低,不适合用于偏移速度分析.本文基于Du和Hou[19]提出的弹性Kirchhoff偏移方法,提取纵波和转换横波局部偏移距域共成像点道集,在Fourier域转化为纵波和转换横波角度域共成像点道集.利用导出的弹性波角度域共成像点道集剩余时差公式,依据本文提出的纵波和转换横波成像深度一致性准则和角度域共成像点道集拉平准则,对纵波和横波的偏移速度进行更新.在此基础上,建立了弹性波偏移速度分析方法流程.
2 基于共炮点道集偏移的角度域共成像点道集提取方法基于波动方程的弹性波成像方法精度高,但比较耗时,且需要较大内存.在弹性波成像过程中还会产生一种固有假象,即纵波反射同相轴会以横波速度在错误的深度位置成像;转换横波同相轴也会以纵波速度在错误的深度位置成像,这种假象会给偏移速度分析带来困难.
Du和Hou[19]提出了一种利用矢量外推标量成像的弹性波Kirchhoff偏移方法,该方法在成像过程中较好地保持了波场的弹性性质,能够消除弹性波成像过程中的固有假象,且计算效率比较高.他们给出的弹性波Kirchhoff偏移公式如下:
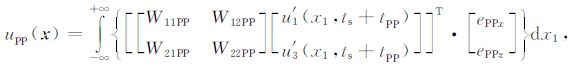
|
(1) |
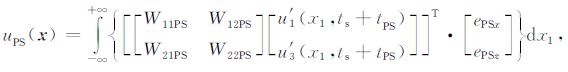
|
(2) |
其中,
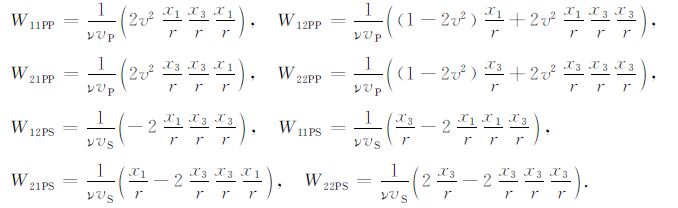
|
ui(x1,t)(i=1,3)表示i方向的位移,i=1表示水平方向,i=3表示垂直方向;u′i(x1,t)(i=1,3)表示i方向的位移对时间的一阶偏导数;r为成像点与记录点之间的距离;ν=vS/vP 为横波与纵波的速度比;x1 代表水平方向,x3 代表垂直方向;x为成像点位置,ePP =ePPxi+ePPzk为成像点处PP波的极化方向的单位矢量,ePS =ePSxi+ePSzk为成像点处PS波的极化方向的单位矢量,ts 为炮点到成像点的走时,tPP 为纵波接收点到成像点的走时,tPS 为横波接收点到成像点的走时.
基于弹性波Kirchhoff叠前深度偏移方法,本文提出了如下的弹性波角度域共成像点道集提取方法.
2.1 PP波角度域共成像点道集提取对弹性波Kirchhoff偏移方法引入空移成像条件可以得到PP 波(纵波入射、纵波反射)局部偏移距域共成像点道集,再通过公式(3)就可以在Fourier域将局部偏移距域共成像点道集转化为角度域共成像点道集[7].
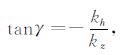
|
(3) |
其中,kh和kz分别代表水平偏移距和深度方向的波数,γ 为入射角.
PP波角度域共成像点道集提取流程如下:
(1) 对单炮多分量地震数据依据弹性波Kirchhoff偏移方法进行多分量Kirchhoff偏移,成像时引入空移成像条件进行成像,获得单炮偏移提取的PP波局部偏移距域共成像点道集R(si,m,h).
(2) 对所有炮进行步骤(1)的处理,并将相同成像点处单炮提取的局部偏移距域共成像点道集按对应偏移距进行叠加,从而得到由全部记录贡献得到的局部偏移距域共成像点道集R(m,h).
(3) 将局部偏移距域共成像点道集进行二维傅里叶变换得R(km,kh).
(4) 将傅里叶域的局部偏移距域共成像点道集按角度等间隔进行插值映射得R(km,γ).
(5) 将R(km,γ)沿km方向进行一维反傅里叶变换得R(m,γ).
2.2 PS波角度域共成像点道集提取由于PS 转换横波(纵波入射、横波反射)传播路径的非对称性,PS波的角度域共成像点道集的提取过程相对PP 波要复杂一些.首先通过弹性波Kirchhoff偏移方法进行多分量Kirchhoff偏移,成像时引入空移成像条件进行成像,得到PS 转换波局部偏移距域共成像点道集.通过公式(4)将局部偏移距域共成像点道集转化为以半孔径角θ 为函数的PS转换波角度域共成像点道集(PS-ADCIGs)[9]:
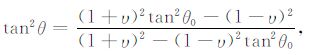
|
(4) |
其中,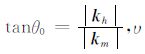
事实上,上述PS-ADCIGs也可以通过公式(5)将其转换为以纵波入射角Φ 为函数的角度域共成像点道集,即P-ADCIGs[10]:
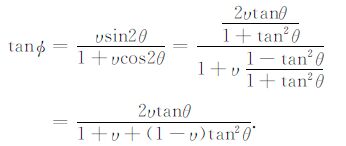
|
(5) |
也可以通过公式(6)将其转换为以反射横波的反射角σ 为函数的角度域共成像点道集,即S-ADCIGs[10]:
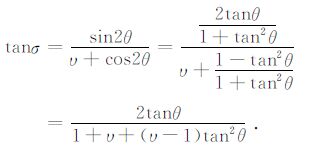
|
(6) |
考虑到目前多采用炸药震源激发三分量接收的多波多分量地震勘探方法,本文选取了以纵波入射角为参数进行转换波角度域共成像点道集(P-ADCIGs)的提取,下文不涉及S-ADCIGs.
PS波角度域共成像点道集提取的流程如下:
(1) 对单炮多分量地震数据依据弹性波Kirchhoff偏移方法进行多分量Kirchhoff偏移,成像时引入空移成像条件进行成像,获得单炮偏移提取的PS波局部偏移距域共成像点道集R(si,m,h).
(2) 对所有炮进行步骤(1)的处理,并将相同成像点处单炮提取的局部偏移距域共成像点道集按对应偏移距进行叠加,从而得到由全部记录贡献得到的PS波局部偏移距域共成像点道集R(m,h).
(3) 将PS 波局部偏移距域共成像点道集进行二维傅里叶变换得R(km,kh).
(4) 应用公式(4)将傅里叶域的PS波局部偏移距域共成像点道集按角度等间隔进行插值映射得R(km,θ).
(5) 将R(km,θ)沿km方向进行一维反傅里叶变换得R(m,θ).
(6) 应用式(5)将R(m,θ)转化为R(m,Φ).
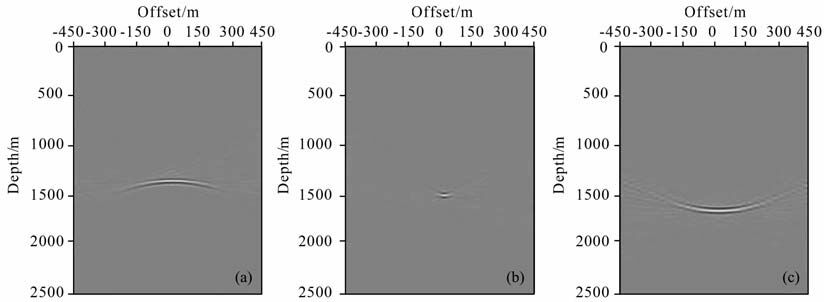
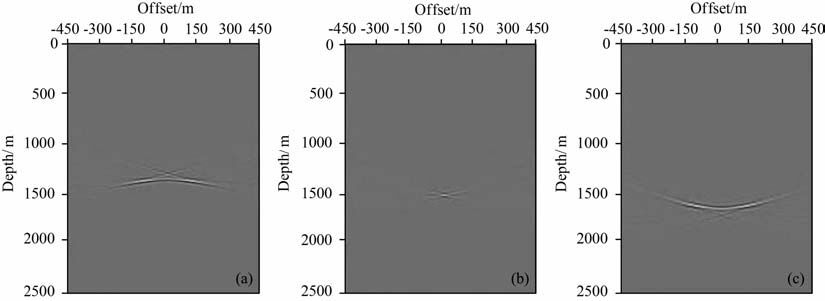
2.3 弹性波角度域共成像点道集提取方法数值实验针对单一水平反射层模型进行试算,图 1为提取的纵波局部偏移距域共成像点道集,图 2 是提取的转换波局部偏移距域共成像点道集.图 1(a,b,c)分别为偏移纵波速度与模型纵波速度的比值等于0.9,1.0,1.1的情况;图 2(a,b,c)分别为偏移横波速度与模型横波速度的比值等于0.9,1.0,1.1的情况.由图 1和图 2 可以看出,当偏移速度正确的时候,无论是纵波还是转换波能量都聚焦到零偏移距附近;当偏移速度过小时,偏移距域同相轴上凸;当偏移速度过大时,偏移距域同相轴下凹.
|
图 1 纵波偏移距域共成像点道集 (a)0.9; (b) 1; (c) 1.1. Fig. 1 P-wave SODCIGs with different ratios of the P-wave migration velocity to the P-wave model velocity |
|
图 2 转换波偏移距域共成像点道集 (a)0.9; (b) 1; (c) 1.1. Fig. 2 PS-wave SODCIGs with different ratios of the shear wave migration velocity to shear wave model velocity (a) 0.9 ; (b) 1 ; (c) 1.1 |
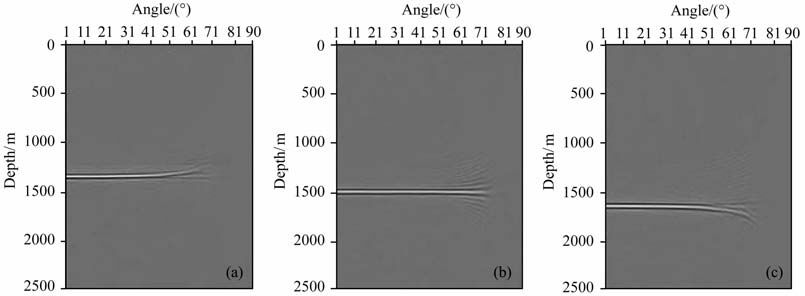
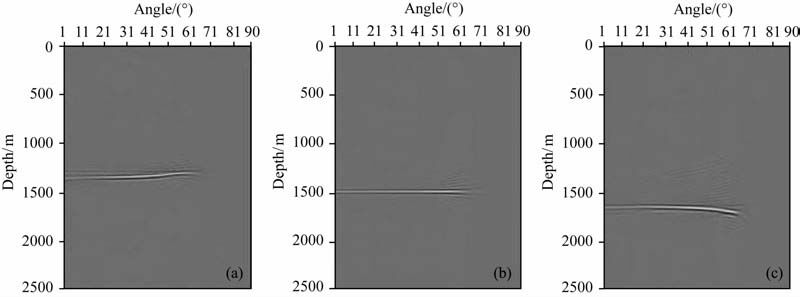
图 3、4分别是图 1、2通过径向道变换得到的角度域共成像点道集.与常规的炮域共成像点道集一致,当偏移速度过小时(如图 3a和图 4a),角度域共成像点道集同相轴表现为上翘;当偏移速度过大时(如图 3c和图 4c),角度域共成像点道集同相轴表现为下弯;当偏移速度等于介质真实速度时(如图 3b和图 4b),角度域共成像点道集同相轴表现为水平.这些性质在反射角比较大的时候更加明显.
|
图 3 纵波角度域共成像点道集 (a) 0.9;(b) 1;(c) 1 1 Fig. 3 P-wave ADCIGs with different ratios of the migration velocity to the model velocity |
|
图 4 转换波角度域共成像点道集 (a)0.9; (b) 1; (c) 1.1. Fig. 4 PS-wave P-ADCIGs with different ratios of the migration velocity to the model velocity |
基于声波理论提取角度域共成像点道集进行偏移速度分析,一般采用角度域共成像点道集是否拉平原则作为判断速度是否准确的准则.然而,基于多分量弹性波Kirchhoff偏移提取的角度域共成像点道集进行偏移速度分析时得到了两个剖面:纵波偏移剖面和转换横波偏移剖面;偏移速度分析道集也得到了两个成像道集:纵波角度域共成像点道集和转换横波角度域共成像点道集.由于二者都是对地下同一地质体地质结构的反映,因此,从理论上来说,在深度域二者应完全一致.为此,本文相应地扩展了角度域共成像点道集是否拉平的判别准则,提出了如下的偏移速度分析准则:
(1) 角度域共成像点道集拉平准则;
(2) 反射纵波和转换横波成像深度一致性原则(即同一反射层所产生的反射纵波和转换横波的成像深度相同).
3.2 速度更新方程速度判别准则只能定性地判断偏移速度是否准确,当偏移速度不准确时还需要对当前偏移速度进行更新.更新速度场需要依据纵波及转换横波共成像点道集速度更新方程进行,即成像深度与速度误差和角度的关系方程.经推导PP 波的速度更新方程(详见附录A)为
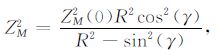
|
(7) |
其中,R为纵波真实速度与偏移速度的比值,通过扫描R值来更新纵波速度.
PS转换横波的速度更新方程(详见附录B)为
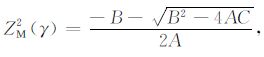
|
(8) |
其中,
R为横波真实速度与偏移速度的比值,通过扫描R值来更新横波速度.
3.3 纵波偏移速度分析流程①由纵波叠加速度场通过Dix公式计算得到纵波层速度场,并在整个工区内进行插值和平滑,获得偏移网格点上的速度作为初始纵波偏移速度场.
② 用当前建立的偏移速度场依据弹性波Kirchhoff偏移方法对多分量地震数据进行单炮弹性波Kirchhoff偏移.在偏移过程中,采用空移成像条件对反射纵波进行成像.
③对所有炮重复步骤②,并将各炮获得的同一共成像点道集叠加在一起,获得反射纵波局部偏移距域共成像点道集.
④对反射纵波局部偏移距域共成像点道集应用Fourier域径向道变换,将反射纵波局部偏移距域共成像点道集转化为反射纵波角度域共成像点道集.
⑤由浅层到深层逐层进行纵波偏移速度分析和速度更新.当前分析层角度域共成像点道集没有拉平时,用公式(7)计算纵波速度更新量,获得新的纵波偏移速度场,并做适当的平滑处理.
⑥重复步骤②~⑤直到当前层的反射纵波角度域共成像点道集拉平为止.
⑦重复步骤②~⑥直到所有速度分析层都分析完为止,并输出最终纵波层速度场.
3.4 横波偏移速度分析流程由PP 波偏移速度分析建立纵波偏移速度场后,就可以利用纵波速度场和初始横波速度场进行横波偏移速度分析.
①由转换横波叠加速度分析建立的转换横波均方根速度通过Dix 公式计算得到转换横波层速度场,并在整个工区内进行插值和平滑.进而通过前述分析得到的纵波速度场和转换横波速度场,根据公式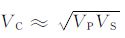
②用当前建立的横波偏移速度场和已经分析获得的纵波偏移速度场对多分量地震数据进行单炮弹性波Kirchhoff偏移.在偏移过程中,采用空移成像条件对转换横波进行成像.
③对所有炮重复步骤②,并将各炮获得的同一共成像点道集叠加在一起,获得PS 转换横波局部偏移距域共成像点道集.
④对PS转换横波局部偏移距域共成像点道集应进行角度分解,将PS 转换横波局部偏移距域共成像点道集转化为PS 转换横波角度域共成像点道集.
⑤由浅层到深层逐层进行横波偏移速度分析和速度更新,当前分析层PS 转换横波角度域共成像点道集没有拉平时,用公式(8)计算横波速度更新量,获得新的横波偏移速度场,并做适当的平滑处理.
⑥重复步骤②~⑤直到当前层的PS转换横波角度域共成像点道集拉平为止.
⑦重复步骤②~⑥直到所有速度分析层都分析完为止,并输出最终横波偏移速度场.
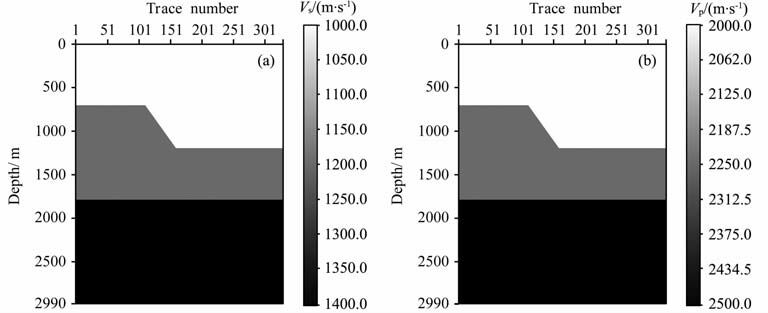
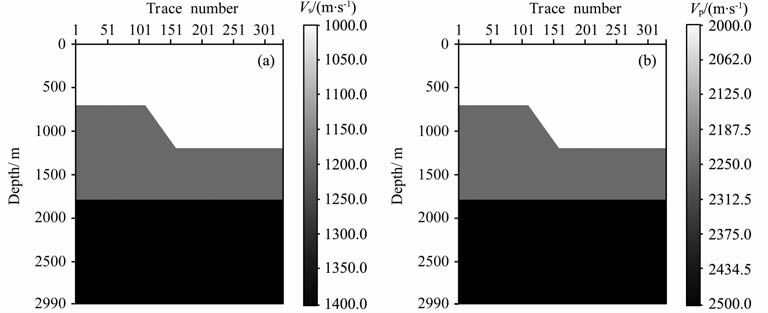
4 模型测试为了验证本文方法的有效性,选用断层模型进行测试.图 5中偏移速度分析的具体过程采用层剥离的方式,由上至下逐层进行偏移速度分析.每隔20个道号选取速度分析的一个控制点,下面以地面道号132处(对应于地下倾斜断面处)的角度域共成像点道集为例,说明偏移速度分析的过程.首先利用叠加速度分析得到初始速度场,图 6 表示了利用本文方法进行速度更新的过程和偏移成像剖面.(a)、(b)是利用初始速度场得到的转换波角度域共成像点道集和纵波角度域共成像点道集,可以看出,无论是纵波还是转换波的角道集上,同相轴都是向上弯曲的,说明速度偏小.分别利用转换波和纵波速度更新公式进行校正,(c)、(d)、(e)是利用多次更新后的速度场得到的转换波角度域共成像点道集、纵波角度域共成像点道集、转换波和纵波叠合在一起的弹性波角度域共成像点道集.图中可以看出,两层对应的同相轴都是拉平的,两种波型成像深度一致,表明所获得的纵横波偏移速度场已正确.(f)、(g)是最终得到的横波偏移速度场和纵波偏移速度场.(h)、(i)是转换波偏移叠加剖面和纵波偏移叠加剖面,两个偏移剖面都已准确成像.
|
图 5 5模型速度场 (a)横波;(b)纵波. Fig. 5 Velocity field (a) Shear wave; (b) P-wave. |
|
图 6 弹性波偏移速度分析 (a)转换波初始角道集;(b)纵波初始角道集;(c)更新后的转换波角道集;(d)更新后的纵波角道集;(e)更新后的 弹性波角道集;(f)横波偏移速度场;(g)纵波偏移速度场;(h)转换波偏移叠加剖面;(i)纵波偏移叠加剖面. Fig. 6 Elastic wave migration velocity analysis (a) Initial angle domain common image gathers of converted wave; (b) Initial angle domain common image gathers of P-wave; (c) Updated PS-wave P-ADCIGs; (d) Updated P-wave ADCIGs; (e) Updated elastic wave ADCIGs; (f) Shear wave final migration velocity; (g) P-wave final migration velocity; (h) PS-wave migration section; (i) P-wave migration section. |
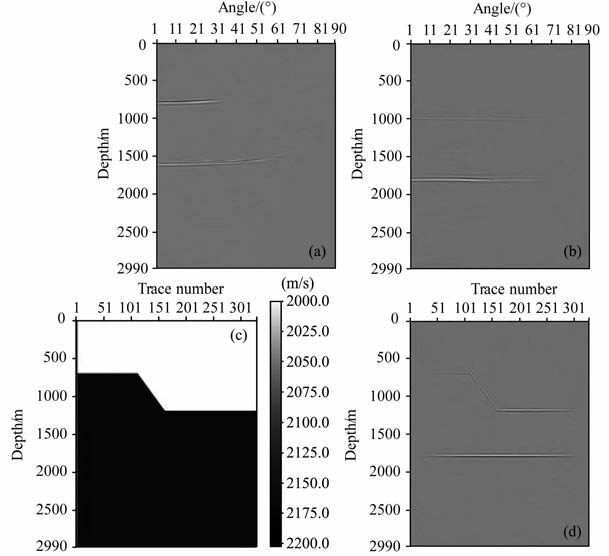
图 7利用声波偏移方法进行偏移速度分析只提供了纵波角道集,对于该断层模型同样获得了高质量的角道集和偏移速度.但从声波角道集图 7b可以看出,由于缺少弹性波成像深度一致性原则的约束,第一层(断层处)的同相轴能量低于图 6d,说明利用空移成像条件下的弹性波偏移方法可以得到能量更聚焦的角道集.另外,从偏移叠加剖面可以看出,在声波偏移剖面图 7d上,地面道号110~160之间(对应于地下倾斜断面)的能量低于图 6i,说明由于弹性波成像深度一致性原则的约束,弹性波偏移方法能得到更加清晰的偏移叠加剖面.当速度误差较大的时候,会有更多的不确定性.当处理复杂模型和实际资料时,利用弹性波成像深度一致性原则可以更好地约束速度更新过程.
|
图 7 声波方法速度更新 (a)初始角道集;(b)更新后的角道集;(c)偏移速度场;(d)偏移剖面. Fig. 7 Acoustic wave migration velocity analysis (a) Initial angle domain common image gathers; (b) Updated ADCIGs; (c) Migration velocity field; (d) Migration section. |
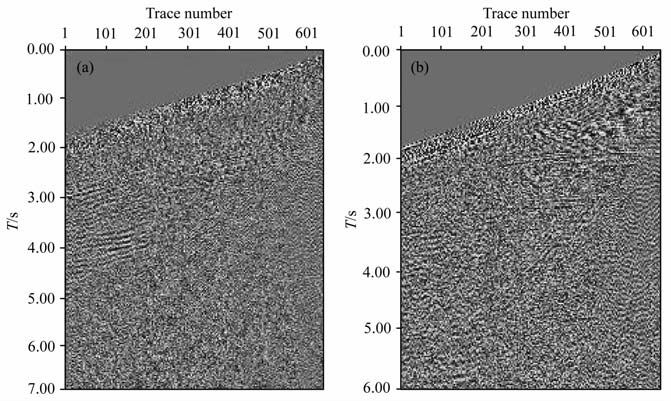
图 8为K71地区野外数据单炮记录水平分量和垂直分量.其观测系统参数如下:道间距5m、最小炮检距5m、最大炮检距3200 m、采样率2ms、X分量采样点数3501、Z分量采样点数3001.
|
图 8 野外单炮记录 (a)X分量;(b)Z分量. Fig. 8 Single shot-gathers of real data (a) Horizontal component; (b) Vertical component. |
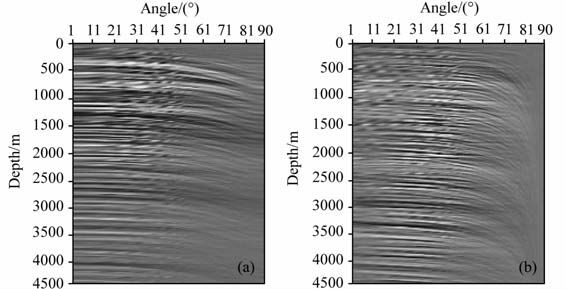
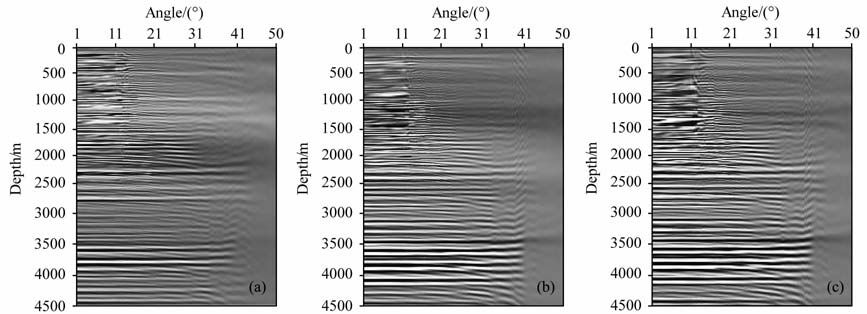
图 9为横波初始速度场(a)和纵波初始速度场(b).图 10为利用初始速度场得到的转换波初始角度域共成像点道集(a)和纵波初始角度域共成像点道集(b).图中可以看出,同相轴向下弯曲,说明速度偏大.采用层剥离的方式,由上至下逐层进行速度更新,图 11 为经过三次迭代后获得的地表位置为6000m 处的转换波角度域共成像点道集(a)和纵波角度域共成像点道集(b)以及两个道集叠加在一起的弹性波角度域共成像点道集(c).由图 11 中可以看出,无论是转换波角度域共成像点道集还是纵波角度域共成像点道集的同相轴都已拉平.在弹性波角度域共成像点道集上,转换波角度域共成像点道集和纵波角度域共成像点道集的对应同相轴重合,满足了弹性波成像深度一致性准则,表明纵波偏移速度场与横波偏移速度场都已合理地重建.

|
图 9 初始速度场 (a)横波;(b)纵波. Fig. 9 Initial velocity fields (a) Shear wave; (b) P-wave. |
|
图 10 初始角道集 (a)转换波;(b)纵波. Fig. 10 Initial angle domain common image gathers (a) Converted wave; (b) P-wave. |
|
图 11 角度域共成像点道集 (a)转换波;(b)纵波;(c)弹性波. Fig. 11 ADCIGs (a) PS-wave P-ADCIGs; (b) P-wave ADCIGs; (c) P- and PS converted waves joint ADCIGs |
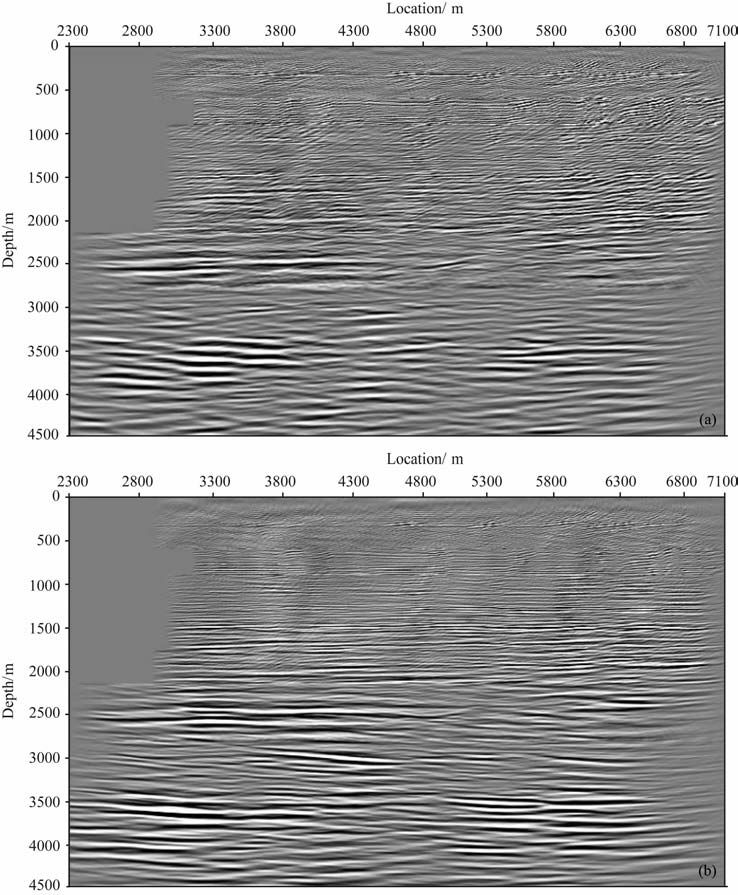
图 12为最终分析获得的横波偏移速度场(a)和纵波偏移速度场(b).图 13为转换波偏移叠加剖面(a)和纵波偏移叠加剖面(b).从两个偏移叠加剖面对比来看,两个剖面波组对应关系比较好,构造位置清晰.

|
图 12 偏移速度场 (a)横波;(b)纵波. Fig. 12 Final migration velocity fields (a) Shear wave; (b) P-wave. |
|
图 13 弹性波弹性偏移成像结果 (a)转换波;(b)纵波. Fig. 13 Elastic Kirchhoff migration sections (a) PS-wave; (b) P-wave. |
本文基于弹性Kirchhoff偏移,对多分量地震数据先进行基于空移成像条件的单炮弹性波Kirchhoff偏移,再对各炮结果进行叠加得到弹性波局部偏移距共成像点道集.在成像点附近局部范围内可以认为满足常速假设,从而可以通过角度分解的方法将弹性波局部偏移距域共成像点道集转化为弹性波角度域共成像点道集.在弹性波角度域共成像点道集的提取过程中,每一道的提取都用到了所有炮和所有偏移距的地震记录的信息,其成像过程满足成像方程,因而能够适应复杂构造情况下多路径情况.通过应用角度域共成像点道集拉平准则和反射纵波和转换横波成像深度一致性原则联合约束偏移速度的准确性.当道集存在剩余时差时,应用纵波角度域共成像点道集速度更新方程和转换波角度域共成像点道集速度更新方程进行纵波和横波速度更新.反射纵波和转换横波成像深度一致性准则可以更加严格地约束纵波与转换横波的角度域共成像点道集,相互制约,可以提高速度分析的精度.实际资料处理表明该方法是行之有效的.
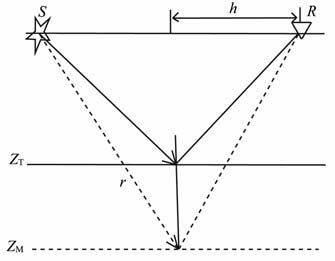
附录A 纵波角度域速度更新方程如图 A1,假设偏移成像点与真实反射点位置在横向上的偏差可以忽略不计.设半偏移距为h,介质真实速度为VT,偏移速度为VM ,偏移深度为ZM ,反射层真实深度为ZT,反射角为γ,偏移距为零时对应的深度为ZM(0).
|
图 A1 反射纵波传播路径示意图 Fig. A1 Sketch map of PP-wave propagation path and imaging path |
偏移时的双程走时为:
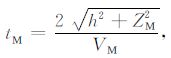
|
(A1) |
同相轴真实的双程走时为:
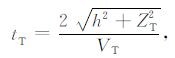
|
(A2) |
根据走时相等原理,可得:

|
(A3) |
令VT/VM =R,考虑到h=ZMtan(γ),可得:
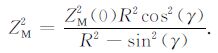
|
(A4) |
通过扫描R值更新纵波速度.
附录B 转换波角度域速度更新方程如图 B1所示,设纵波半偏移距为hp,转换横波半偏移距为hs,介质纵波速度为Vp,横波偏移速度为VSM ,横波真实速度为VST,偏移深度为ZM ,反射层真实深度为ZT,纵波入射角为Φ,横波反射角为σ.
|
图 B1 转换波传播路径示意图 Fig. B1 Sketch of PS-wave propagation path and imaging path |
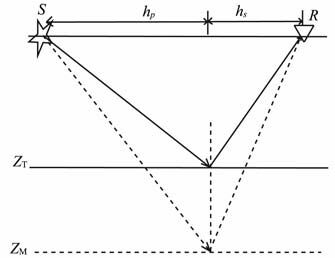
由图B1可得,
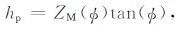
|
(B1) |
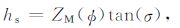
|
(B2) |
偏移时的双程走时为
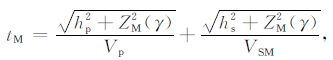
|
(B3) |
同相轴真实的双程走时为
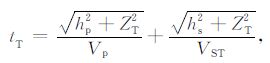
|
(B4) |
根据走时相等原理,可得:
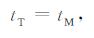
|
(B5) |
令

|
则
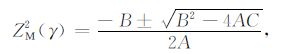
|
(B6) |
如果A为负,考虑到C为正,则
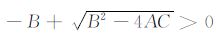
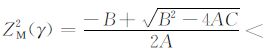
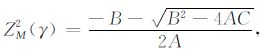
|
(B7) |
通过扫描R值更新横波速度.由Snell定律得,

|
这样在已知VSM 和Vp 的情况下就可以计算式(B7)所描述的曲线.
事实上,要使A满足A<0,经推证只需满足如下条件:
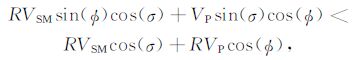
|
(B8) |
在0~90°的角度域道集中自然满足sin(Φ)<1,因此RVSMsin(Φ)cos(σ)一定小于RVSMcos(σ).当偏移速度大于真实速度时,则R>1;在0~90°的角度域道集中也自然满足sin(σ)< 1,因而可得VPsin(σ)cos(Φ)<RVPcos(Φ).因此,只要偏移速度大于真实速度,(B8)一定满足.
当偏移速度小于真实速度时,在角度不是很大或速度误差不是很大的情况下,则能够满足sin(θ)<R,因此(B8)式也是满足的.
实际情况下,(B8)式并非完全满足,此时A为非负数.当出现A为非负的情况,利用速度分析过程的交互性,根据道集的性质(上翘或下弯),给定小的速度扰动,以达到速度更新的目的.
| [1] | ten Kroode A P E, Smit D J, Verdel A R. A microlocal analysis of migration. Wave Motion , 1998, 28(2): 149-172. DOI:10.1016/S0165-2125(98)00004-3 |
| [2] | Nolan C J, Symes W W. Imaging and coherency in complex structure. 66th Ann. Internat Mtg., Soc. Expl. Geophys. Expanded Abstracts , 1996: 359-363. |
| [3] | Nolan C J, Symes W W. Global solution of a linearized inverse problem for the wave equation. Communications in Partial Differential Equations , 1997, 22(5&6): 919-952. |
| [4] | Prucha M B, Biondi B, Symes W W. Angle-domain common image gathers by wave-equation migration.69th Ann. Internat Mtg., Soc. Expl. Geophys. Expanded Abstracts , 1999: 824-827. |
| [5] | Xie X, Wu R. Extracting angle domain information from migrated wavefield. 72nd Ann. Internat Mtg., Soc. Expl. Geophys. Expanded Abstracts , 2002: 1360-1363. |
| [6] | Sava P, Fomel S, Biondi B. Amplitude-preserved common image gathers by wave-equation migration. 71th Ann. Internat Mtg., Soc. Expl. Geophys. Expanded Abstracts , 2001: 296-299. |
| [7] | Sava P, Fomel S. Angle-domain common-image gathers by wavefield continuation methods. Geophysics , 2003, 68(3): 1065-1074. DOI:10.1190/1.1581078 |
| [8] | 陈生昌, 马在田, 吴如山. 波动方程角度域共成像点道集. 地球科学-中国地质大学学报 , 2007, 32(4): 569–574. Chen S C, Ma Z T, Wu R S. Angle domain common image gather for wave equation. Diqiu Kexue-Zhongguo Dizhi Daxue Xuebao/Earth Science-Journal of China University of Geosciences (in Chinese) , 2007, 32(4): 569-574. |
| [9] | Sava P, Fomel S. Wave-equation common-angle gathers for converted waves. 75th Ann. Internat Mtg., Soc. Expl. Geophys. Expanded Abstracts , 2005: 947-950. |
| [10] | Rosales D A, Fomel S, Biondi B L, et al. Wave-equation angle-domain common-image gathers for converted waves. Geophysics , 2008, 73(1): S17-S26. DOI:10.1190/1.2821193 |
| [11] | Rosales D A, Biondi B L. Converted-waves angle-domain common-image gathers. 75th Ann. Internat Mtg., Soc. Expl. Geophys. Expanded Abstracts , 2005: 959-962. |
| [12] | Biondi B L, Symes W W. Angle-domain common-image gathers for migration velocity analysis by wavefield-continuation imaging. Geophysics , 2004, 69(5): 1283-1298. DOI:10.1190/1.1801945 |
| [13] | Biondi B L, Tisserant T. 3-D angle-domain common-image gathers for migration velocity analysis. Geophysical Prospecting , 2004, 52(6): 575-591. DOI:10.1111/gpr.2004.52.issue-6 |
| [14] | Sava P, Biondi B L. Wave-equation migration velocity analysis-I: Theory. Geophysical Prospecting , 2004, 52(6): 593-606. DOI:10.1111/gpr.2004.52.issue-6 |
| [15] | Sava P, Biondi B. Wave-equation migration velocity analysis-II: Subsalt imaging examples. Geophysical Prospecting , 2004, 52(6): 607-623. DOI:10.1111/gpr.2004.52.issue-6 |
| [16] | Xia F, Ren Y, Jin S. Residual migration-velocity analysis using common angle image gathers. 76th Ann. Internat Mtg., Soc. Expl. Geophys. Expanded Abstracts , 2006: 2455-2459. |
| [17] | 刘守伟, 王华忠, 程玖兵, 等. 时空移动成像条件及偏移速度分析. 地球物理学报 , 2008, 51(6): 1883–1891. Liu S W, Wang H Z, Cheng J B. Space-time-shift imaging condition and migration velocity analysis. Chinese J Geophys. (in Chinese) , 2008, 51(6): 1883-1891. |
| [18] | Zhang K, Li Z C, Zeng T S, et al. Residual curvature migration velocity analysis for angle domain common imaging gathers. Applied Geophysics , 2010, 7(1): 49-56. DOI:10.1007/s11770-010-0006-1 |
| [19] | Du Q Z, Hou B. Elastic Kirchhoff migration of vecterial wave-fields. Applied Geophysics , 2008, 5(4): 284-293. DOI:10.1007/s11770-008-0045-z |
 2011, Vol. 54
2011, Vol. 54

