2. 中国地震局地壳应力研究所,北京 100085;
3. 中国地震台网中心,北京 100045
2. Institute of Crustal Dynamics, China Earthquake Administration, Beijing 100085, China;
3. China Earthquake Network Center, Beijing 100045, China
地幔黏度存在剧烈的径向变化[1, 2]和强烈的横向变化[3].地幔横向黏度变化虽然不能对地幔对流形态起控制性作用[4~6],但会对对流状态和格局、相变动力学、地球内部热结构、板块动力学以及地球物理观测场等产生显著的影响[5~15],同时还可以在均匀边界条件下获得环型场分量[5, 16].朱涛等[17]曾对小横向黏度变化的情形进行过深入的研究,获得的地幔浅部极型场和环型场对流形态对认识和理解现今地表构造的运动状态提供了帮助.然而,由于小横向黏度变化的假设,在朱涛等[17]的求解过程中并没有实行交叉迭代,使得地幔对流的极型场和环型场的耦合只停留在理论意义上.针对这种情形,本文将地幔横向黏度变化提高到3 个量级,在求解过程中实施了交叉迭代,实现了地幔对流的极型场和环型场的相互耦合.依此获得的地幔浅部的极型场和环型场对流形态得到了显著的改善,能更合理地解释太平洋板块向西或西北、大洋洲向北或北北东、南美洲向西的运动状态以及北太平洋板块的右旋运动.同时揭示出东太平洋洋中脊与极型场对流的发散区对应更好,这为更深入地认识和理解现今地表构造运动的深部动力学过程提供了有益的帮助.
2 基本公式考虑内径为R1,外径为R2 充满了不可压缩的牛顿流体的同心球层,纯粹从球层底部加热,采用Boussinesq近似,并取流体的普朗特数无限大(Pr=ν/κ,ν为运动学黏度;κ 为热扩散系数.地球地幔的普朗特数约1024[18]),球层中流体的黏度为流体平均黏度η0 加上横向黏度变化\[\tilde \eta \],则在球坐标系(r,θ,φ)中控制变黏度流体运动的无量纲方程组见文献[4]中的式(1).将速度场u分解为极型标量场Φ 和环型标量场ψ[19],对动量方程(文献[4]中的式(1b))两边分别施加算子(r· Δ×)和(Λ· Δ×),可得到关于环型场ψ 和极型场Φ 表达式
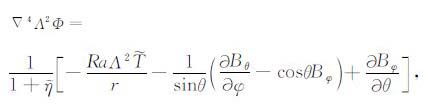
|
(1a) |
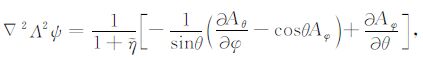
|
(1b) |
其中,
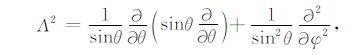
|
(1c) |
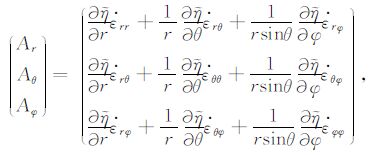
|
(1d) |
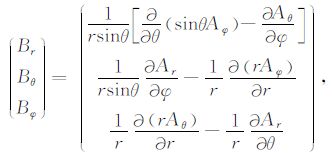
|
(1e) |
其中,${{\dot{\varepsilon }}_{ij}}$为应变率,$\tilde{T}$ 为扰动温度,Ra为瑞利数.式(1)和热传输方程(文献[4]中的式(1c))共同组成了求解大横向黏度变化下地幔对流模型的基本方程组.可以看出,式(1a)和(1b)比小横向黏度变化情况下[16]均多了一项1/(1+\[\tilde \eta \]),其他项均相同.在求解小横向黏度变化下的地幔对流模型时,忽略了式(1a)中因横向黏度变化(右端第二项)而产生的极型场成分[16],没有实施交叉迭代来求解极型和环型标量场,即极型场与环型场并没有实现真正意义上的耦合.在本文中,\[\tilde \eta \] 的变化会达到3个量级,因此在求解极型场时不能忽略式(1a)右端第二项,在求解过程中需进行交叉迭代式(1a)和(1b),从而实现极型场与环型场真正意义上的耦合.显然,这种耦合肯定会调整极型场和环型场的对流格局,使得本文的结果比小横向黏度变化下的结果[17]更接近真实情形,为更深入理解和认识横向黏度变化对地幔动力学的影响提供有益的帮助.
在此跟小横向黏度变化下的情形一样[17],研究了上边界为刚性或应力自由,下边界为应力自由等温边界的情形,其数学形式为:
上、下均为应力自由等温边界(F-F边界)
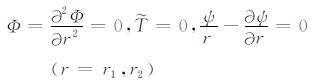
|
(2) |
上边界为刚性、下边界为应力自由等温边界(R-F边界)
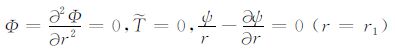
|
(3a) |
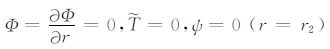
|
(3b) |
其中,r1 和r2 分别为球层内径R1、外径R2 的无量纲值.
3 横向黏度变化形式室内实验表明,地幔的黏度强烈依赖于温度、压力和应力(或应变率)[20].有效黏度可以表述为
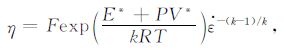
|
(4) |
其中E* ,V* 分别为激活能和体积,F为常量,R是气体常量,T为温度,k是幂率指数.在文中,采用了Zhang和Christensen[21]研究中的黏度形式,

|
(5) |
其中H(r)是与随深度变化相关的压力、平均温度、平均应变率和矿物结构等引起的径向分层黏度.δρ为密度异常.ω 是小量,是为了防止$\dot{\varepsilon }\to $0时而导致黏度变为无穷大.常量c描述在黏度随温度线性变化和黏度随温度指数变化的假设下黏度的变化.对于一次近似,c可以根据式(6)计算
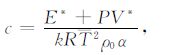
|
(6) |
其中T 为平均温度.令式(6)中的幂率指数k=1时,则获得随温度变化的黏度,此时为牛顿黏度.所以式(6)变为
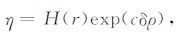
|
(7) |
在此,用地幔平均黏度η0 来替代分层黏度H(r),便可获得横向黏度变化的分布
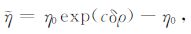
|
(8) |
显然,对于等黏度地幔,常量c=0.0,即其最小值为0.0,而其最大值据Zhang和Christensen估计可能不超过1.0 m3/kg[21].用地幔平均黏度η0 对式(8)进行无量纲化后可得
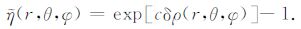
|
(9) |
本文的横向黏度变化形式与朱涛等[17]研究小横向黏度变化下的地幔对流相同.可通过式(10)由地震波速异常而获得.然后通过式(9)可获得横向黏度变化$\tilde{\eta }$,它具有三维分布形式.
假定地幔中地震波速异常对应的地幔横向不均匀结构是地幔热对流的结果,则可以将地震波速异常通过式(10)转换为地幔密度异常[22].
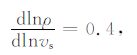
|
(10a) |
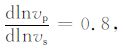
|
(10b) |
其中,ρ 为地幔密度.vs、vp 分别为地震横波和纵波速度.
4 球函数展开将极型标量场Φ、环型标量场ψ、扰动温度场珦T和横向黏度变化\[\tilde \eta \] 展成复球谐形式,分别如下
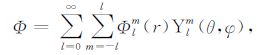
|
(11a) |
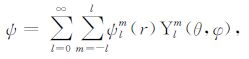
|
(11b) |
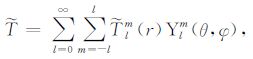
|
(11c) |
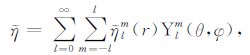
|
(11d) |
其中,Ylm(θ,φ)是正规化的l阶m级面谐函数,

|
(12) |

|
(13) |
其中,Plm(cosθ)是正规化的l阶m级的缔合勒让德函数.面谐函数的正交归一关系为
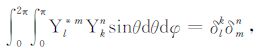
|
(14) |
其中,Yl*m是Ylm的共轭.将式(1a)和(1b)展开为球谐形式为
当t≠0时,
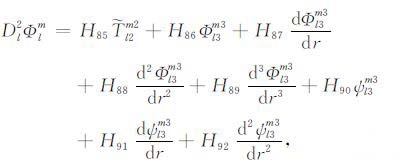
|
(15a) |
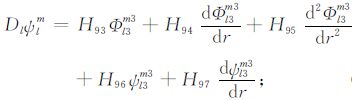
|
(15b) |
当l=0,且l1 =l2 =l3 =0时,
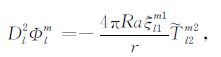
|
(16a) |
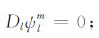
|
(16b) |
当l=0,且l1,l2,l3 不同时为零时,
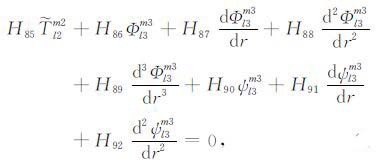
|
(17a) |
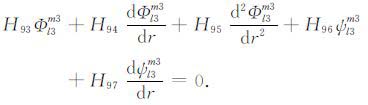
|
(17b) |
其中,
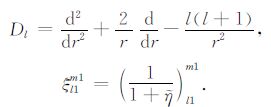
|
积分系数H1 ~ H97 的表达式见附录A.对于式(17),其系数H85 ~ H97 比附录A 中的减少一项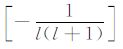
将热传输方程(文献[4]中的式(1c))展开成球谐形式为
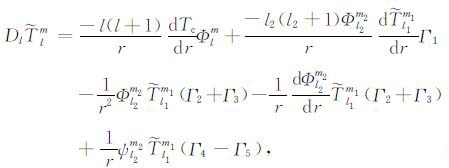
|
(18) |
其中,Tc 是无对流运动时的温度场,仅是径向r的函数,满足热传导方程Δ2Tc=0.积分系数Γi(i=1,2,3,4,5)的表达式见附录B.将边界条件(3)展开成球谐形式为
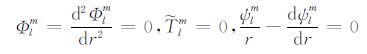
|
(19a) |
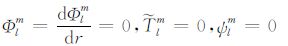
|
(19b) |
Galerkin方法是将连续问题转换为离散问题的一种方法.Zebib 等[23]、叶正仁等[24]以及朱涛和冯锐[25]将之用来求解地幔对流模型.在此,也采用Galerkin方法来进行求解.设
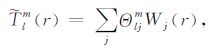
|
(20a) |
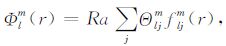
|
(20b) |
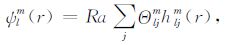
|
(20c) |
取基函数
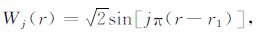
|
(21) |
则Θlmj自然满足关于温度的边界条件.将式(20)和(21)代入式(15)~(19),并利用三角函数的正交性可得
当l≠0时,
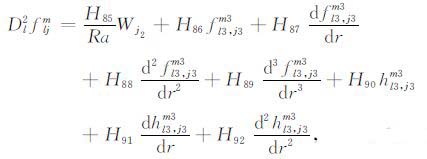
|
(22a) |
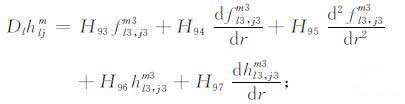
|
(22b) |
当t=0,且t1 =t2 =t3 =0时,
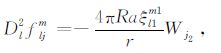
|
(23a) |
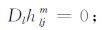
|
(23b) |
当l=0,且l1,l2,l3 不同时为零时,
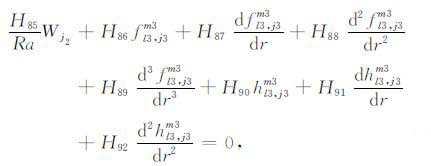
|
(24a) |
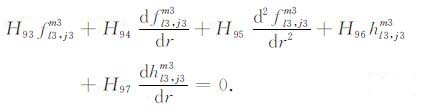
|
(24b) |
对于F-F边界条件,
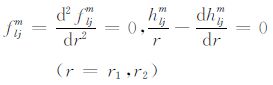
|
(25) |

|
(26a) |
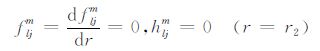
|
(26b) |
对于热传输方程式(18),
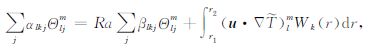
|
(27) |
其中,
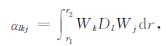
|
(28a) |
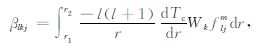
|
(28b) |
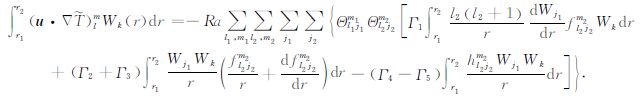
|
(28c) |
由此通过式(22)~(24)和边界条件(25)或(26)求解出fljm和hljm,然后通过式(27)求解出Θljm,最后利用式(20)求出珦Tlm、Φlm、ψlm,便可获得对流图像.
6 结果及分析为了与小横向黏度变化下的结果对比,在文中采用了与文献[17]相同的参数,即球谐展开的最大阶数取lmax= 6,同时取jmax=kmax=6.R1=3471km,R2=6271km,它们分别对应于核幔边界和岩石圈底界面的位置.瑞利数Ra=106.地球地幔的地震波速异常采用SH12WM13模型求得[25].沿经度、纬度和深度方向上采用144×72×56 的网格(相当于平面上2.5°×2.5°的网格,深度上每层厚度为50km),利用PREM 地球模型[26]以及地震波速异常和密度之间的转换关系(10)计算地幔密度异常,然后利用式(9)获得地幔内部的横向黏度变化.一般情况下,横向黏度变化的最大值出现在上地幔和下地幔中,达到了2~4个量级,而中地幔则为1~2个量级[3],因此文中在将密度异常转换为横向黏度变化时,通过选择合适的常量c,将横向黏度的变化控制在3个量级内.
由于上、下地幔密度异常最大值是不同的,因此在将密度异常转换成横向黏度变化时,需选择不同的常量c.在文中,对于上地幔,利用SH12WM13模型[24]求得的正、负密度异常绝对值的最大值均出现在约100km 深度处,分别约为83.11kg/m3 和58.63kg/m3,用式(9)可获得常量c分别约为0.083m3/kg和0.118m3/kg;而对于下地幔,正、负密度异常绝对值的最大值分别出现在约2550km和2700km 深度处,约为38.10kg/m3 和55.63kg/m3,则常量c分别约为0.181m3/kg和0.124m3/kg.图 1显示了200km、300km、400km 深度处横向黏度变化的分布图像.图 1揭示出,大陆下的横向黏度变化基本为正值,而大洋下,除了200km 深度处太平洋中部的横向黏度变化为正值外,其他区域基本为负值;在上地幔,横向黏度变化剧烈程度随深度而降低,且变化最剧烈的区域也随深度而不同:对大陆而言,200km 深度处横向黏度变化最剧烈的区域位于北美大陆下,最大横向黏度变化约309.0(无量纲值);300km 深度处出现在欧亚大陆下,最大横向黏度变化约137.5;400km 深度处则出现在欧亚、澳洲及非洲北部大陆下,最大横向黏度变化约27.1.对海洋而言,200km、300km 和400km 深度处均出现在东太平洋区域,最大横向黏度变化绝对值分别约240.7、48.6 和34.0.文中提供的不同深度的横向黏度变化(图 1)的这些特征是由地幔中密度异常的分布来决定的(见式(9)).
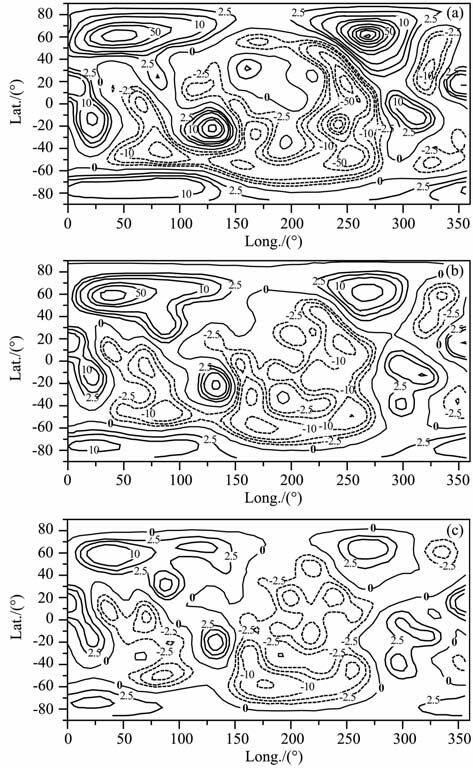
|
图 1 不同深度处无量纲横向黏度变化分布 a)200 km;(b)300 km;(c) 400 km.图中等值线值的顺序为: —250,一200,一150,一100, —50,一30,一10,一5,一2.5, 0, 2.5, 5, 10, 30, 50, 100, 150, 200, 250, 300. Fig. 1 The contours of dimensionless lateral variable viscosity at different depths The contours are arranged in the sequence of 一 250,一 200, 一150,一100,一50,一30,一10,一5,一2.5,0,2.5,5,10, 30, 50,100,150, 200, 250, 300. |
在数值离散过程中,对一阶和三阶偏微分采用向前差分格式,对二阶和四阶则采用向后差分格式.对非线性方程组采用Levenberg-Marquardt 方法[27]进行求解.两种方式验证了计算程序的可靠性[4].
6.2 极型场对流图像图 2显示了深度为200km 处R-F 和F-F 边界下的极型场对流图像与地表构造的关系.与文献[17]中的图 3对比发现,本文结果相对于小横向黏度变化下的结果具有较好的改善.主要体现在太平洋板块、大洋洲和南美洲下的对流运动方向以及东太平洋洋中脊处对流状态.本文结果明显揭示出太平洋板块向西或西北、大洋洲向北或北北东、南美洲向西的运动状态以及对流发散区与东太平洋洋中脊的良好对应.而小横向黏度变化下,两种边界下的极型场对流图像难以明显揭示出现今地表板块的运动状态(图 3).对于欧亚大陆、非洲大陆以及北美洲下的对流运动状态,没有明显的改善.
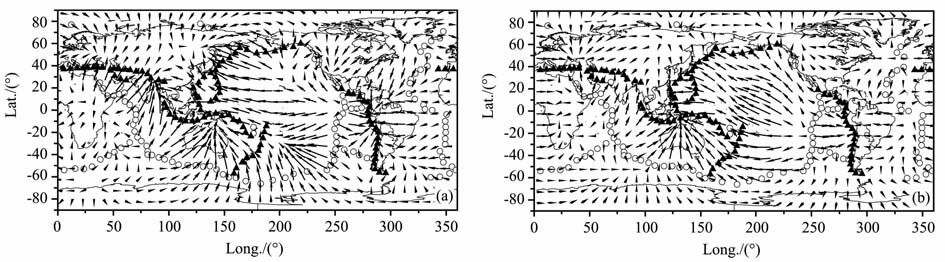
|
图 2 深度为200 km处不同边界条件的极型场对流图像和地表构造的关系 (a)R-F边界,最小速率0. 45 cm/a,最大速率19. 54 cm/a; (b)F-F边界,最小速率0.07 cm/a, 最大速率16. 42 cm/a.其中黑实三角代表汇聚带,空心圆圈代表发散带,下图同. Fig. 2 The relations between the poloidal convection patterns at 200 km depth under different boundary conditions and surface tectonics (a) R-F boundary,the ma:ndary, the minimum velocity 0. 45 cm/a, the maximum velocity 19. 54 cm/a; (b) F-F boundary, the minimum velocity 0. 07 cm/a imum velocity 16. 42 cm/a . Black triangles represent convergent zones and circles represent divergent zones. The same below. |
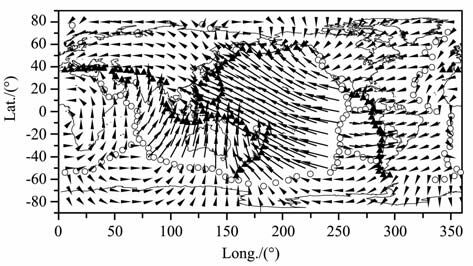
|
图 3 根据HS2-NUVEL1模型获得现今地表板块的 运动状态.最小速率0.15 cm/a,最大速率10.9 cm/a Fig. 3 The current motion states of surface plates from HS2-NUVEL1 model. The minimum velocity 0.15 cm/a, the maximum velocity 10. 9 cm/a |
图 2揭示出,对流运动在碰撞带(如喜马拉雅-阿尔卑斯碰撞带)和俯冲带(如西太平洋俯冲带)表现出汇聚流,而在洋中脊(如东太平洋、印度洋、大西洋洋中脊)则表现为发散流.对流速度较大的区域主要集中在西太平洋俯冲带和洋中脊附近.洋中脊如东太平洋和印度洋洋中脊两侧对流运动速率存在明显差异.这些结果与HS2-NUVEL1 模型获得的地表板块运动状态(图 3)比较一致.与小横向黏度下的结果一样,本文结果(图 1,特别是图 1a)也揭示出在非洲大陆的东北部下存在一个对流运动的发散中心,其北或北北东向对流速率明显较大,这或许是东非大裂谷形成的深部动力学原因.
300km 深度处R-F边界下极型场对流图像(图 4a)与200km 深度处的(图 2a)非常相似,也与地表大型构造带具有良好的对应关系.但400km 深度处R-F边界下极型场对流图像(图 4b)与200km(图 2a)和300km(图 4a)的特征存在明显的差异,主要体现在东太平洋、印度洋洋中脊处和非洲大陆下的对流发散区的消失以及印度洋板块下东北部对流运动速率的明显减小.这些现象可能表明与欧亚大陆作用的印度洋板块的主体为400km 以上的部分;产生东太平洋洋中脊和东非大裂谷的地幔热柱主要存在于400km 以浅.

|
图 4 R-F边界下不同深度的极型场对流图像 (a)300 km,最小速率 0. 13cm/a,最大速率 19. 62cm/a; (b) 400 km,最小速率 0. 36cm/a,最大速率 12. 13cm/a. Fig. 4 The relations between the poloidal convection patterns at ditferent depths under R-F boundary and surface tectonics (a) 300 km, the minimum velocity 0. 13 cm/a, the maximum velocity 19. 62 cm/a;(b) 400 km, the minimum velocity 0. 36 cm/a, the maximum velocity 12. 13 cm/a. |
从图 2和图 4看出,本文计算的极型场对流运动的最大速率已经明显大于现今板块运动的总速率(图 3),这可能是在计算中引入的约束不够的缘故.
6.3 环型场对流图像图 5显示了200km 深度处R-F 和F-F 边界条件下的环型场对流图像与地表构造的关系.与小横向黏度变化下的环型场对流图像(文献[17]中的图 5)相比,图 5主要改善之处为北太平洋下的环型场对流的旋转中心的位置更偏北以及南美洲和东太平洋边界处的旋转状态.通过与图 5 中显示的现今板块运动的径向涡度(radialvorticity)的等值线[28]进行对比,发现这种改善使得本文获得的环型场对流比小横向黏度变化下的更加合理.
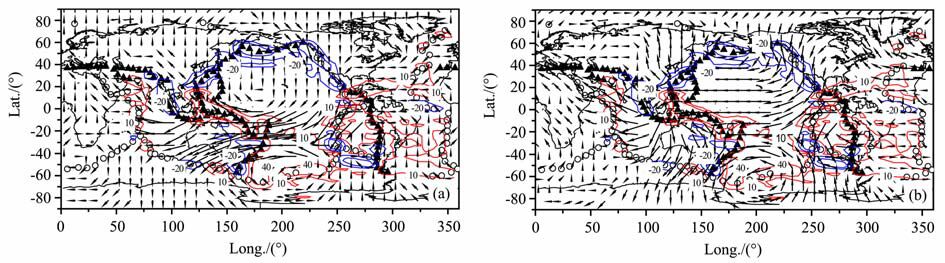
|
图 5 不同边界条件下200 km深度处环型场对流图像与地表构造的关系 (a)R-F边界,最小速率0.02 cm/a,最大速率2.09 cm/a;b)F-F边界,最小速率0. 05 cm/a,最大速率2.90 cm/a.蓝色实线代表负的 涡度等值线(即顺时针循环),红色实线代表正的涡度等值线,等值线间隔为30X10-9rad/a,每条等值线值等于标度值X10-9rad/a. Fig. 5 The relations between the toroidal convection patterns at 200 km depth under different boundary conditions and surface tectonics (a) R-F boundary, the minimum velocity 0. 02 cm/a, the maximum velocity 2. 09 cm/a; (b) F-F boundary, the minimum velocity 0. 05 cm/a,the maximum velocity 2. 90 cm/a. Blue solid lines represent the contours of negative vorticity (i. e. clockwise circulation) , red ones represent the contours of positive vorticity. The interval between two adjacent contours is 30X 10_9 rad/a. The value of each contour is equal to the scale multiplied by 10_9 rad/a. |
图 5揭示出总体上北半球处于右旋、南半球处于左旋循环对流状态,并且在赤道附近区域存在自东向西的环型场对流条带,在条带的两侧对流速率总体上存在差异:北半球对流速率相对较大且主要存在于环赤道低纬度区域,而南半球相对较小,这种差速流动或许是导致环赤道大型剪切系统[29]及影响其强震活动的深部动力学原因.
对比图 2和图 5可以看出,计算的环型场对流速率远远小于极型场对流速率,这与现今板块运动的极型场与环型场能量几乎相等的事实还存在显著差异.同时使得地幔对流总速度场与极型场速度分布特征几乎相同(图 6).
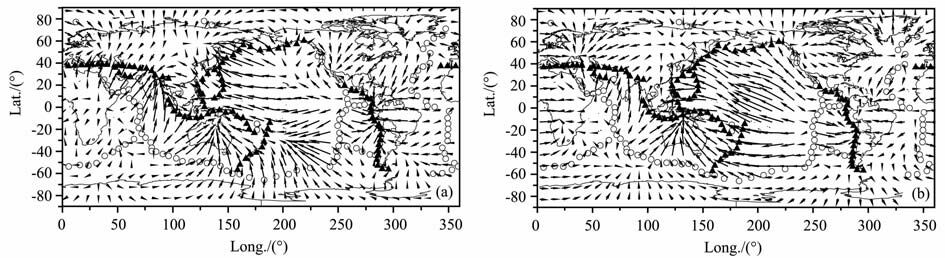
|
图 6 深度为200 km处不同边界条件的总速度场和地表构造的关系 (a)R-F边界,最小速率0. 33cm/a,最大速率19. 61cm/a; (b)F-F边界,最小速率0. 57cm/a,最大速率25. 00 cm/a. Fig. 6 The relations between the total convection patterns at 200 km depth under different boundary conditions and surface tectonics (a) R-F boundary, the minimum velocity 0. 33 cm/a» the maximum velocity 19. 61 cm/a; (b) F-F boundary, the minimum velocity 0. 57 cm/a, the maximum velocity 25. 00 cm/a. |
本文的结果相对于小横向黏度变化下的结果具有显著的改善.通过与地表板块运动进行对比分析后,发现本文的结果更加合理.这可能要归功于两个方面.首先,本文将横向黏度变化的量级显著提高,达到了3个量级.横向黏度变化大小的改变对计算结果进行了合理的调节;其次,由于横向黏度变化量级的提高,使得在求解过程须经过交叉迭代,这就使得极型场和环型场达到了真正的耦合,从而结果更趋合理.不过,计算获得的极型场对流最大速率明显大于、环型场对流最大速率明显小于现今地表板块运动的最大速率;某些区域如欧亚大陆和非洲大陆下的对流状态与现今地表板块的运动状态有较大差异.
自20世纪80年代以来,很多研究者已经对环型场的产生机制及其地球物理意义做过深入的研究.主要从两个方面入手.首先,利用运动板块激发地幔的环型对流.在这类模型中,一般要求板块内部为刚性,而边界则为变形区域(黏度比内部低得多),并且作用于板块的总应力或力矩为零.研究结果表明,能获得能量几乎相等的极、环型场和良好的地表速度场以及大地水准面异常的拟合,但是环型场能量随着深度会快速衰减,主要存在于上地幔中,而极型场却在整个层中相对稳定(除两个边界处有所衰减外)[30~33].然而,由于板块边界处应力奇点的存在导致施加于旋转板块上的力矩趋于无穷会导致模型不自恰;其次,利用地幔黏度横向变化产生环型对流.地幔黏度横向变化的引入,即使在均匀边界下,也能够自然地获得环型场分量.计算的环型场对流速率远远小于极型场对流速率[7, 16],本文的结果与此一致,但与板块运动的极型场分量和环型场分量功率几乎相等具有明显差异.由此,建立同时包含了板块自身运动和地幔黏度横向变化的对流模型可能对解释地表观测能提供更大的帮助.
附录A
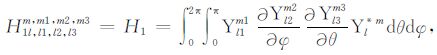
|
(A1) |
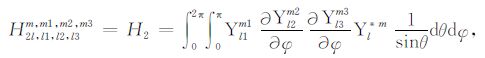
|
(A2) |
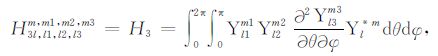
|
(A3) |
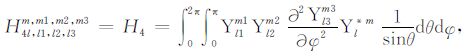
|
(A4) |
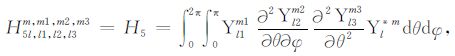
|
(A5) |
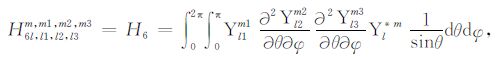
|
(A6) |
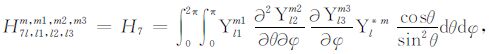
|
(A7) |
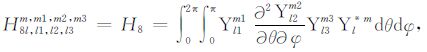
|
(A8) |
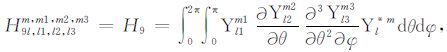
|
(A9) |

|
(A10) |
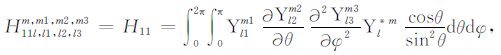
|
(A11) |
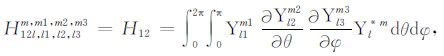
|
(A12) |
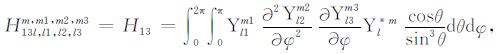
|
(A13) |
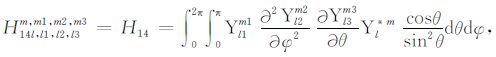
|
(A14) |
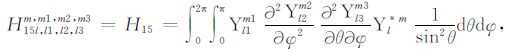
|
(A15) |
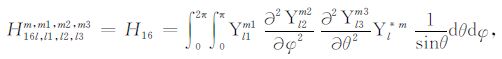
|
(A16) |

|
(A17) |
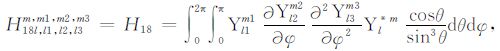
|
(A18) |
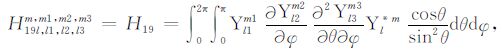
|
(A19) |
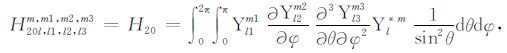
|
(A20) |
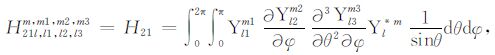
|
(A21) |
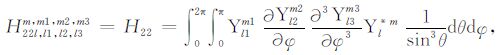
|
(A22) |
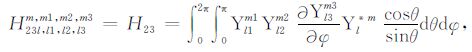
|
(A23) |
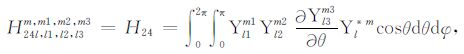
|
(A24) |
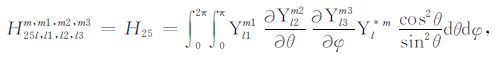
|
(A25) |
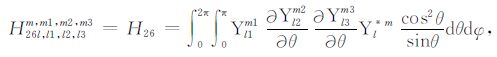
|
(A26) |
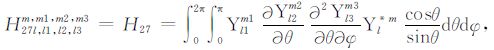
|
(A27) |
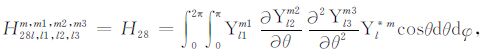
|
(A28) |
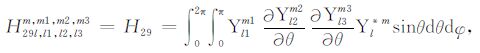
|
(A29) |
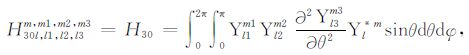
|
(A30) |
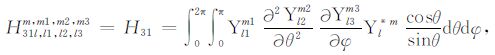
|
(A31) |
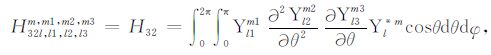
|
(A32) |
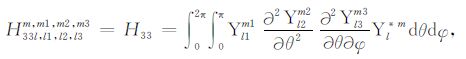
|
(A33) |
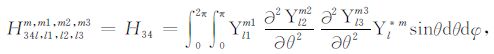
|
(A34) |
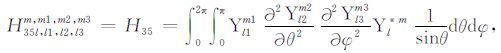
|
(A35) |
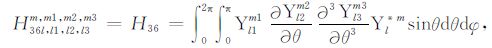
|
(A36) |
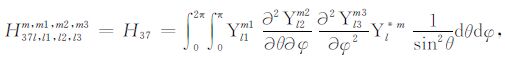
|
(A37) |
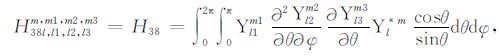
|
(A38) |
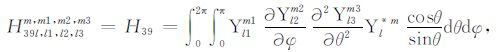
|
(A39) |

|
(A40) |
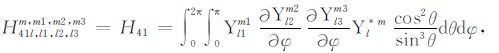
|
(A41) |
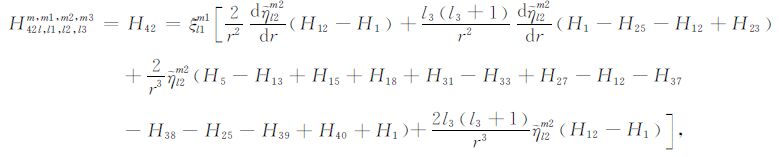
|
(A42) |
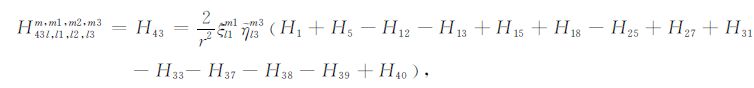
|
(A43) |
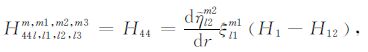
|
(A44) |
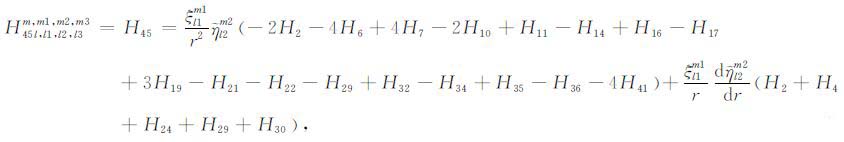
|
(A45) |
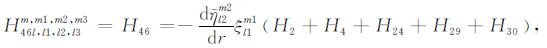
|
(A46) |
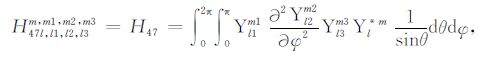
|
(A47) |
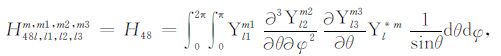
|
(A48) |

|
(A49) |
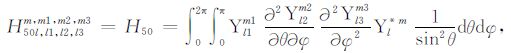
|
(A50) |
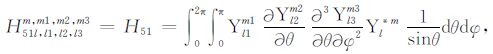
|
(A51) |
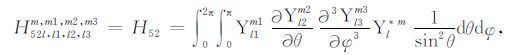
|
(A52) |
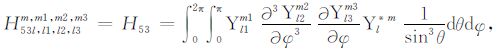
|
(A53) |
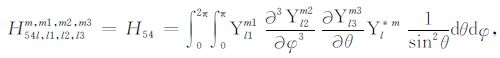
|
(A54) |
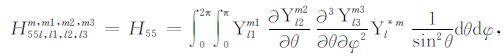
|
(A55) |
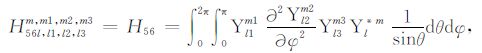
|
(A56) |
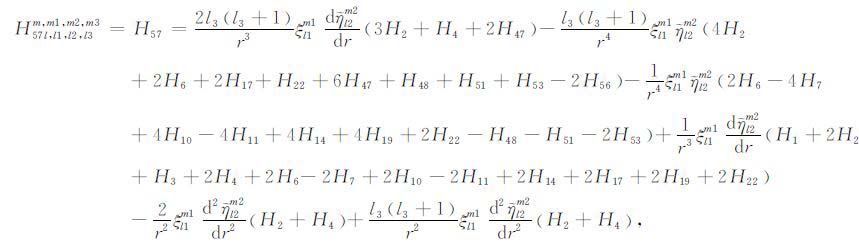
|
(A57) |
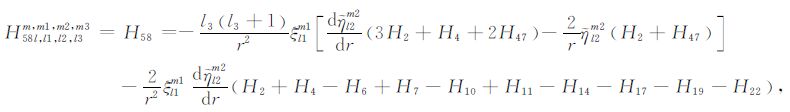
|
(A58) |
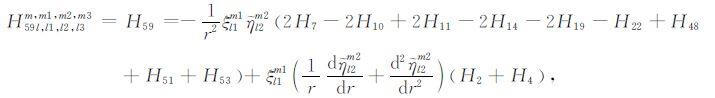
|
(A59) |
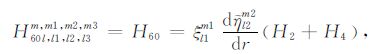
|
(A60) |
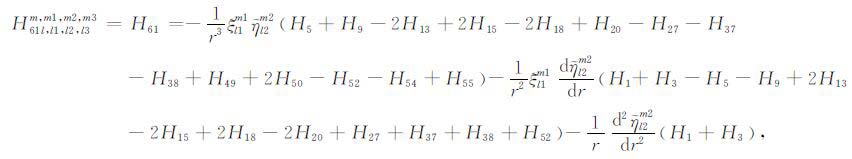
|
(A61) |
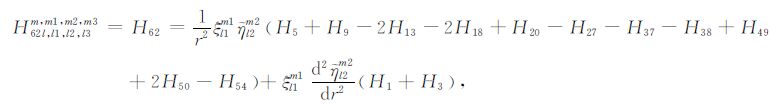
|
(A62) |
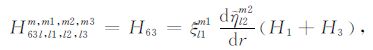
|
(A63) |
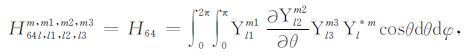
|
(A64) |
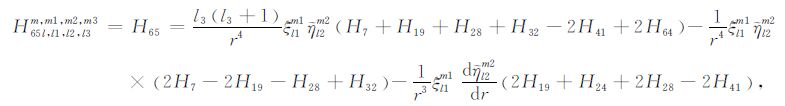
|
(A65) |
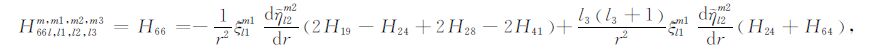
|
(A66) |
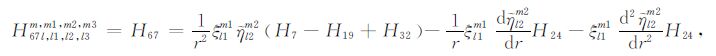
|
(A67) |
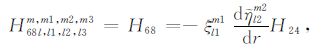
|
(A68) |
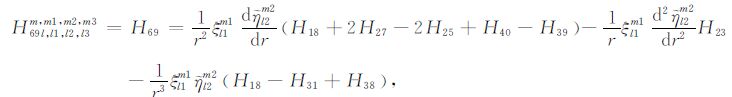
|
(A69) |
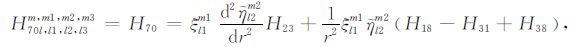
|
(A70) |
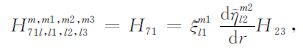
|
(A71) |
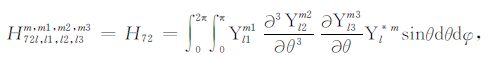
|
(A72) |
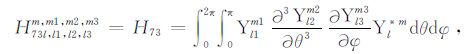
|
(A73) |
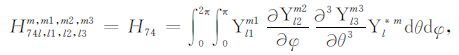
|
(A74) |
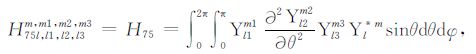
|
(A75) |
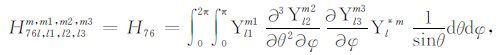
|
(A76) |
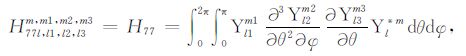
|
(A77) |
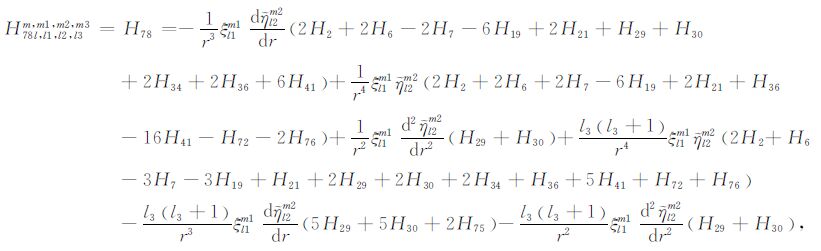
|
(A78) |

|
(A79) |
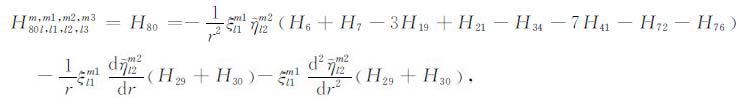
|
(A80) |
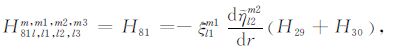
|
(A81) |
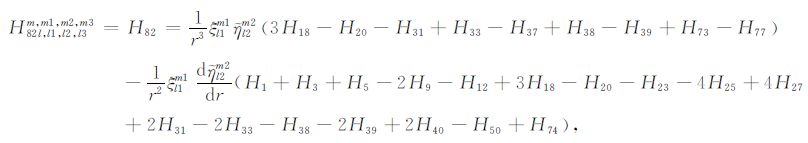
|
(A82) |
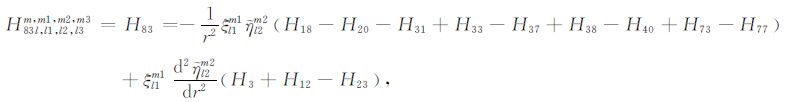
|
(A83) |
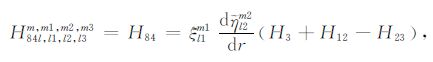
|
(A84) |
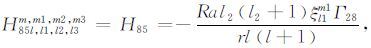
|
(A85) |

|
(A86) |

|
(A87) |
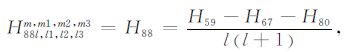
|
(A88) |
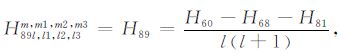
|
(A89) |
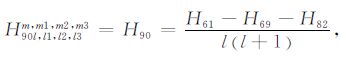
|
(A90) |
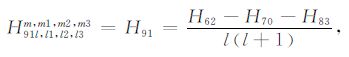
|
(A91) |
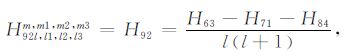
|
(A92) |
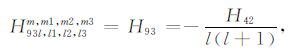
|
(A93) |
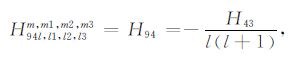
|
(A94) |
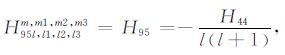
|
(A95) |
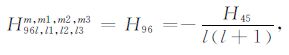
|
(A96) |
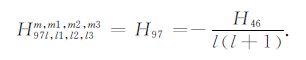
|
(A97) |
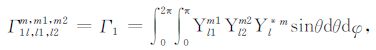
|
(B1) |
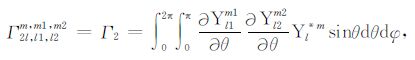
|
(B2) |
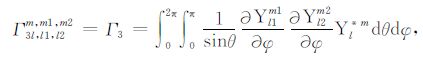
|
(B3) |
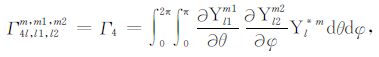
|
(B4) |
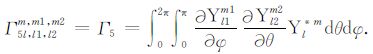
|
(B5) |
| [1] | Hager B H. Subducted slabs and the geoid: constrains on mantle rheology and flow. J. Geophys. Res. , 1984, 89: 6003-6015. DOI:10.1029/JB089iB07p06003 |
| [2] | Mitrovica J X, Peltier W R. Constrains on mantle viscosity based upon the inversion of post-glacial uplift data from the Hudson Bay region. Geophys. J. Int. , 1995, 122: 353-370. DOI:10.1111/gji.1995.122.issue-2 |
| [3] | Ranalli G. Mantle rheology: radial and lateral viscosity variations inferred from microphysical creep laws. Journal of Geodynamics , 2001, 32(4-5): 425-444. DOI:10.1016/S0264-3707(01)00042-4 |
| [4] | 朱涛, 王兰炜, 陈化然. 横向黏度变化对球层中热对流的影响. 地球物理学报 , 2010, 53(2): 350–361. Zhu T, Wang L W, Chen H R. Effects of lateral viscosity variation on thermal convection in a spherical shell. Chinese J. Geophys. (in Chinese) , 2010, 53(2): 350-361. |
| [5] | Ratcliff J T, Schubert G, Zebib A. Steady tetrahedral and cubic patterns of spherical shell convection with temperature-dependent viscosity. J. Geophys. Res. , 1996, 101(B11): 25473-25484. DOI:10.1029/96JB02097 |
| [6] | Stemmer K, Harder H, Hansen U. A new method to simulate convection with strongly temperature-and pressure-dependent viscosity in a spherical shell: Applications to the earth's mantle. Physics of the Earth and Planetary Interiors , 2006, 157: 223-249. DOI:10.1016/j.pepi.2006.04.007 |
| [7] | Christensen U, Harder H. 3 D convection with variable viscosity. Geophys. J. Int. , 1991, 104: 213-226. DOI:10.1111/gji.1991.104.issue-1 |
| [8] | Richards M A, Hager B H. Effects of lateral viscosity variations on geoid anomalies and topography. J. Geophys. Res. , 1989, 94(B8): 10299-10313. DOI:10.1029/JB094iB08p10299 |
| [9] | Zhong S, Zuber M T, Moresi L, et al. Role of temperature-dependent viscosity and surface plates in spherical shell models of mantle convection. J. Geophys. Res. , 2000, 105(B5): 11063-11082. DOI:10.1029/2000JB900003 |
| [10] | Tackley P. Effects of strongly temperature-dependent viscosity on time-dependent, three-dimensional models of mantle convection. Geophys. Res. Lett. , 1993, 20: 2187-2190. DOI:10.1029/93GL02317 |
| [11] | Bunge H, Richards M A. The origin of long scale structure in mantle convection: Effects of plate motions and viscosity stratification. Geophys. Res. Lett. , 1996, 23(21): 2987-2990. DOI:10.1029/96GL02522 |
| [12] | Yoshida M, Nakakuki T. Effects on the long-wavelength geoid anomaly of lateral viscosity variations caused by stiff subducting slabs, weak plate margins and lower mantle rheology. Physics of the Earth and Planetary Interiors , 2009, 172: 278-288. DOI:10.1016/j.pepi.2008.10.018 |
| [13] | adek O, Fleitout L. Effect of lateral viscosity variations in the coremantle boundary region on predictions of the long wavelength geoid. Stud. Geophys. Geod. , 2006, 50: 217-232. DOI:10.1007/s11200-006-0013-0 |
| [14] | Wang H, Wu P. Effects of lateral variations in lithospheric thickness and mantle viscosity on glacially induced relative sea levels and long wavelength gravity field in a spherical, self-gravitating Maxwell Earth. Earth and Planetary Science Letters , 2006, 249: 368-383. DOI:10.1016/j.epsl.2006.07.011 |
| [15] | Oliver D S, Booker J R. Planform of convection with strongly temperature-dependent viscosity. Geophysical & Astrophysical Fluid Dynamics , 1983, 27(1): 73-85. |
| [16] | 朱涛, 冯锐. 球层中的非线性自由热对流——变黏度模型. 地震学报 , 2005, 27(2): 194–204. Zhu T, Feng R. Nonlinear free thermal convection in a spherical shell: A variable viscosity model. Acta Seismologica Sinica (in Chinese) , 2005, 27(2): 194-204. |
| [17] | 朱涛, 马宗晋, 冯锐. 三维地震波速结构约束下的变黏度地幔对流及其动力学意义. 地球物理学报 , 2006, 49(5): 1347–1358. Zhu T, Ma Z J, Feng R. 3-D lateral variable viscosity mantle convection constrained by seismic wave velocity and its geodynamic implications. Chinese J. Geophys. (in Chinese) , 2006, 49(5): 1347-1358. |
| [18] | 傅容珊, 黄建华. 地球动力学. 北京: 高等教育出版社, 2006 . Fu R S, Huang J H. Geodynamics (in Chinese). Beijing: Higher Education Press, 2006 . |
| [19] | Buckus G. A class of self-sustaining dissipative spherical dynamos. Ann. Phys. , 1958, 4: 381-384. |
| [20] | Kirby S H, Kronenberg A K. Rheology of the lithosphere: selected topics. Rev. Geophys. , 1987, 25(6): 1219-1244. DOI:10.1029/RG025i006p01219 |
| [21] | Zhang S, Christensen U. Some effects of lateral viscosity variations on geoid and surface velocities induced by density anomalies in the mantle. Geophys. J. Int. , 1993, 114: 531-547. DOI:10.1111/gji.1993.114.issue-3 |
| [22] | 傅容珊, 董树谦, 黄建华, 等. 地震层析成像—地幔对流新模型的研究. 地球物理学报 , 2002, 45(Suppl): 136–142. Fu R S, Dong S Q, Huang J H, et al. A new mantle convection model constrained by seismic tomography. Chinese J. Geophys. (in Chinese) , 2002, 45(Suppl): 136-142. |
| [23] | Zebib A, Schubert G, Straus J M. Infinite Prandtl number thermal convection in a spherical shell. J. Fluid Mech. , 1980, 97(2): 257-277. DOI:10.1017/S0022112080002558 |
| [24] | 叶正仁, 滕春凯, 张新武. 地幔对流与岩石圈板块的相互耦合及影响——(I)球腔中的自由热对流. 地球物理学报 , 1995, 38(2): 174–180. Ye Z R, Teng C K, Zhang X W. Coupling between mantle circulation and lithospheric plates—(I) Thermal free convection in a spherical shell. Chinese J. Geophys. (Acta Geophysica Sinica) (in Chinese) , 1995, 38(2): 174-180. |
| [25] | 朱涛, 冯锐. 球层中高阶自由热对流格局及其变化的研究. 地震学报 , 2005, 27(1): 11–24. Zhu T, Feng R. The patterns of high-degree thermal free convection and its features in a spherical shell. Acta Seismologica Sinica (in Chinese) , 2005, 27(1): 11-24. |
| [26] | Su W J, Robert L W, Dziewonski A M. Degree 12 model of shear velocity heterogeneity in the mantle. J. Geophys. Res. , 1994, 99(B4): 6945-6980. DOI:10.1029/93JB03408 |
| [27] | Dziewonski A M, Anderson D L. Preliminary reference earth model. Physics of the Earth and Planetary Interiors , 1981, 25: 297-356. DOI:10.1016/0031-9201(81)90046-7 |
| [28] | 杨柳, 陈艳萍. 求解非线性方程组的一种新的全局收敛的Levenberg-Marquardt算法. 计算数学 , 2008, 30(4): 388–396. Yang L, Chen Y P. A new globally convergent Levenberg-Marquardt method for solving nonlinear system of equations. Mathematica Numerica Sinica (in Chinese) , 2008, 30(4): 388-396. |
| [29] | Forte A M, Peltier W R. Plate tectonics and aspherical earth structure: The importance of poloidal-toroidal coupling. J. Geophys. Res. , 1987, 92: 3645-3679. DOI:10.1029/JB092iB05p03645 |
| [30] | 马宗晋. 全球三大构造体系与板条构造. 见:全球构造与固体地球多圈层相互作用. 香山科学会议第143次学术讨论会 , 2000, 143: 14–16. Ma Z J. The earth's three great tectonic systems and plate strip tectonics.In: Coupling between Earth's Tectonics and Multisphere (in Chinese). Xiangshan Scientific Convention (in Chinese) , 2000, 143: 14-16. |
| [31] | Hager B H, O'Connell R J. Kinemetic models of large-scale mantle flow. J. Geophys. Res. , 1979, 84: 1031-1048. DOI:10.1029/JB084iB03p01031 |
| [32] | Richard Y, Vigny C. Mantle dynamics with induced plate tectonics. J. Geophys. Res. , 1989, 94: 17543-17560. DOI:10.1029/JB094iB12p17543 |
| [33] | Gable C W, O'Connell R J. Convection in three dimensions with surface plates: Generation of toroidal flow. J. Geophys. Res. , 1991, 96(B5): 8391-8450. DOI:10.1029/90JB02743 |
| [34] | 叶正仁, 朱日祥. 地幔对流与岩石圈板块的相互耦合及影 响——(II)地幔混合对流理论及其应用. 地球物理学报 , 1996, 39(1): 47–56. Ye Z R, Zhu R X. Coupling between mantle circulation and lithospheric plates—(II) mix convection and its applications. Chinese J. Geophys. (in Chinese) , 1996, 39(1): 47-56. |
 2011, Vol. 54
2011, Vol. 54


