2. 中国科学院计算地球动力学实验室,北京 100049
2. Laboratory of Computational Geodynamics, Chinese Academy of Sciences, Beijing 100049, China
GOCE(Gravity field and steady-state Ocean Circulation Explorer)卫星计划主要目标之一就是利用引力梯度观测值去解算地球引力场(或重力场).由于GOCE 中出现了一类新型的观测量,即:引力梯度,所以如何处理GOCE 数据便成了当前地球引力场研究的热点工作之一.对GOCE 数据处理的研究工作可归纳为下列几个方面:GOCE 引力梯度数据预处理方法和精度分析[1, 2];计算GOCE 卫星轨道的方法[3, 4];利用GOCE 数据来确定引力场的方法以及相应的精度分析等[5~8].
在利用GOCE 数据去解算引力场位系数的方法中较为常见的途径是“法方程方法”,其过程可归结为几个步骤[9~13]:首先是利用卫星姿态建立某已知坐标系与梯度仪坐标系(GRF)之间的转换关系;其次是利用GRF中的引力梯度观测值建立关于地球引力场位系数的观测方程组;最后是对方程组进行求解.法方程方法中的核心技术是大型方程组的解算,这显然是相当复杂的工作.
近来出现了利用引力梯度张量的不变量建立观测方程的方法[14, 15],此时得到的观测方程是扰动位在轨道上的二阶径向导数边界条件,该边界条件的形式简单,适合于利用边值问题的途径来解算引力场的位系数.但由于边值问题应用的前提是边界面应该是球面,因此需要将卫星轨道面上建立的边界条件延拓到相应的平均球面上来,这就产生了引力梯度的归算问题.
为了便于叙述引力梯度归算的重要性,现列举不变量方法的主要结论如下[14]:记v是地球引力位,V是正常引力位(是v足够好的近似,例如:V可取为EGM2008引力场模型等),T=v-V是扰动位,S表示GOCE 卫星的轨道面,通过引入引力梯度不变量后,可以在轨道S上得到

|
(1) |
这里f是与V和v在卫星轨道上梯度值相关的不变量函数(简称为不变量扰动,公式(1)的具体证明见文[14]中公式(8)和(9)).
公式(1)是利用不变量方法导出的观测方程,也可以理解成是轨道上关于扰动位的边界条件.对于如何从公式(1)去求解扰动位T,显然边值问题的途径要比针对位系数的大型方程组的解算更为有效.由于利用球谐调和分析时要求边界面是球面,所以本文的工作就是研究如何将在GOCE 卫星轨道S上的边界条件(1)延拓到轨道的平均球面上以及对延拓的精度作出客观的评价,其结论对于实际处理GOCE 数据有着直接的作用.
2 延拓方法由于GOCE 卫星的轨道是近圆周的(扁心率约为10-3),所以S的形状是接近于球面的.取Σ 是与S在某种意义下最吻合的球面,例如:可以将S上每点至地心的距离的平均值取为Σ 的半径,这样便能得到所需的球面Σ .记P是S上任意一点,而Q是Σ 上沿半径方向与P的对应点,rQP=rP-rQ(这里rP和rQ分别是P和Q到地心的距离),则利用Taylor展开定理,便有
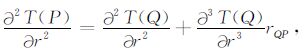
|
(2) |
这里仅保留了rQP的一次项(如果需要的话,可保留至rQP的二次或更高次项).代入公式(1)后便得
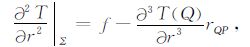
|
(3) |
公式(3)是球面Σ 上的边界条件,该公式是基于Taylor展开而导出的延拓方法.
由于扰动位T是待求的量,因此在实际计算过程必须消除公式(3)中右边显含T的项.下面介绍两种基于公式(3)的实用算法.
2.1 基于扰动位的迭代方法该算法的基本形式是:取T0 =0,以及j>1时

|
(4) |
由此便能逐步解出扰动位.
2.2 基于正常引力位的迭代方法一般而言,正常引力位V的选取原则是尽可能地逼近实际地球的引力位v.若第j次迭代时正常引力位是Vj,可以认为Vj是v足够好的近似,此时按照正常引力位Vj和v的梯度计算出不变量扰动fj,便得关于扰动位的边值问题:
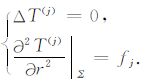
|
(5) |
求解问题(5),可得T(j) .接着继续迭代的形式是:令Vj+1 =Vj+T(j),然后重复进行即可.
需要说明的是:基于正常引力位的迭代方法的本质是将地球引力位v从S延拓到Σ 时所需计算的三阶导数值等同于正常引力位对应的三阶导数值.这样处理的理由是v为待求的量,从而其三阶导数值是未知的,所以延拓过程中必须用某个已知的值替代,自然逐步逼近的正常引力位对应的三阶导数值就成为了选择.另外,对于给出的两种迭代方法,尽管其形式不同,但原理是一致的,这是因为本质上它们都是基于Taylor展开式(3)而产生的.
在完成了将轨道面S上的引力梯度不变量扰动延拓至相应的平均球面上后,可以运用典型的球谐调和分析的方法计算出地球引力场v的位系数,从而完成利用GOCE 观测数据解算地球引力场或者重力场的工作.
3 算 例本节将采用模拟的方法研究引力梯度延拓以及恢复引力场位系数的精度.
3.1 Legendre函数及导数的计算无论是开展GOCE 数据的实际处理、还是进行模拟计算,都会涉及到Legendre函数及其导数的计算问题.事实上,引力梯度的计算与Legendre函数的二阶导数有关,而梯度的延拓则需要进行Legendre函数三阶导数(甚至四阶)的计算.本文中引用的延拓是基于公式(2)的,因此需要研究Legendre函数以及一阶、二阶和三阶导数的计算方法.
本文中对于Legendre函数的计算采用标准的向前迭代法,即:
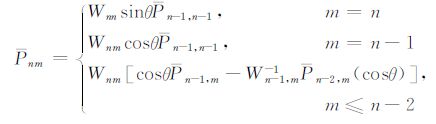
|
(6) |
这里Pnm(t)是规则化后的Legendre函数,0≤θ≤π 是余纬,记号Pnm=Pnm(cosθ),
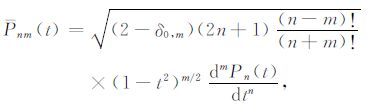
|
(7) |
以及
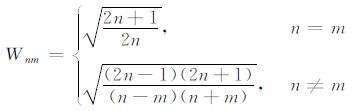
|
(8) |
而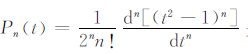
Legendre函数导数的计算将采用下列公式:
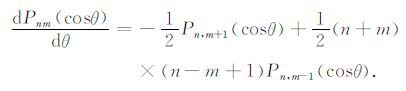
|
(9) |
这里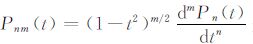
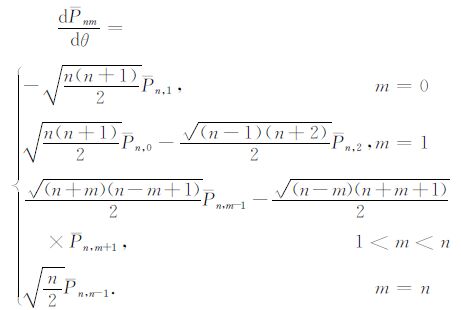
|
(10) |
公式(10)便是Legendre函数导数的计算公式,循环使用能够计算Legendre函数的高阶导数.利用公式(10)计算Legendre函数各阶导数的优点在于能有效地避免地球两极附近的奇异性,从而提高Legendre函数导数的计算精度[16].
3.2 算例与精度评估本文将对边界条件(1)进行模拟延拓计算.模拟对象取为EGM2008 引力场模型的前300 完整阶次,即:
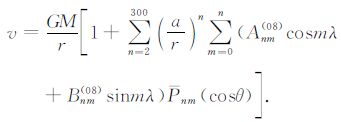
|
(11) |
这里GM是地球的万有引力质量常数,a是赤道半径,λ 是经度,而Anm(08)和Bnm(08)是EGM2008模型中给出的位系数.因为GOCE 卫星轨道的高度大约离地面250km,扁心率约为10-3,考虑到轨道的不规则的特点,所以将卫星轨道的径向摆动适当放大,即假设轨道面S是下列椭球面:
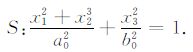
|
(12) |
这里,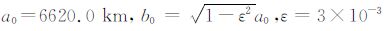
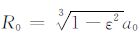
将EGM96 模型的前60 完整阶次取为正常引力位V,即:
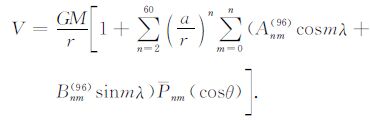
|
(13) |
同样在上述格网上计算对应于V的梯度值,于是在S上便有不变量扰动f以及边界条件(1).注意此时的边界条件(1)是在卫星轨道面S的30′×30′格网上得到的,而S不是球面,因此通常的球谐分析方法不能使用.若要使用球谐分析从条件(1)来解算扰动位,就必须将边界条件(1)归算到球面Σ 上.
为了能够反映出归算的实际精度,令T=v-V是扰动位,并在球面Σ 对应的30′×30′格网上计算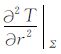
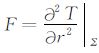
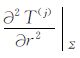
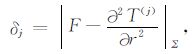
|
(14) |
则δj表示了进行j次引力梯度归算后的精度,特别j=1时
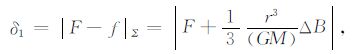
|
(15) |
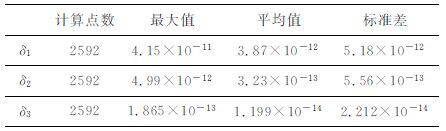
其表示的含义是引力梯度没有进行归算时产生的误差.利用S的30′×30′格网上不变量f的值,在Σ 的5°×5°格网点上分别计算了δ1,δ2 和δ3 的值,其主要统计指标列在表 1中.
|
|
表 1 归算后引力梯度误差的主要统计值(单位:m • s-2) Table 1 The main statistical values for,δ1 (Unit: m • s-2) |
从表 1 中的主要统计结果可知,依据Taylor公式给出的归算方法(3)能有效地提高轨道平均球面上的引力梯度归算值的精度,每次归算大致能提高一个量级的精度.事实上,归算过程中收敛的程度与轨道至平均球面的距离有关,即:若在轨卫星的位置与轨道平均球面相距越远,则归算收敛就越慢;反之,相距越近,则归算收敛就越快.就GOCE 卫星计划而言,根据其轨道设计的特点,预计至多进行2次归算便能达到梯度观测精度3mE 的要求(1 mE=10-12s-2).
为了深入讨论引力场位系数恢复计算的精度问题,我们分别利用已经得到的归算前后引力梯度的值对EGM2008模型前300完整阶次的位系数进行了恢复计算,即:分别就j=1,2,3的情况对边值问题(5)进行了计算,从而还原EGM2008的前300阶位系数.逐次对j=1,j=2和j=3的情况,经计算分别得到了模拟引力位v的逐步逼近解:
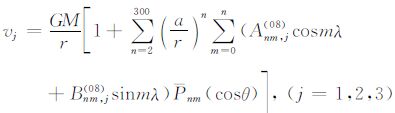
|
(16) |
图 1描述了v的Kaula系数阶方差曲线以及vj对v的位系数逼近阶方差.阶方差描述如下:若v的球谐展开式由公式(11)给出,则
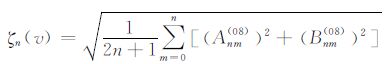
|
(17) |
是v的n阶方差,其按阶数n给出的曲线称为Kaula系数阶方差曲线(简称Kaula 曲线或阶方差);若v与vj分别由公式(11)和(16)给出,则
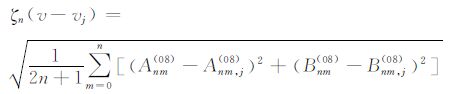
|
(18) |
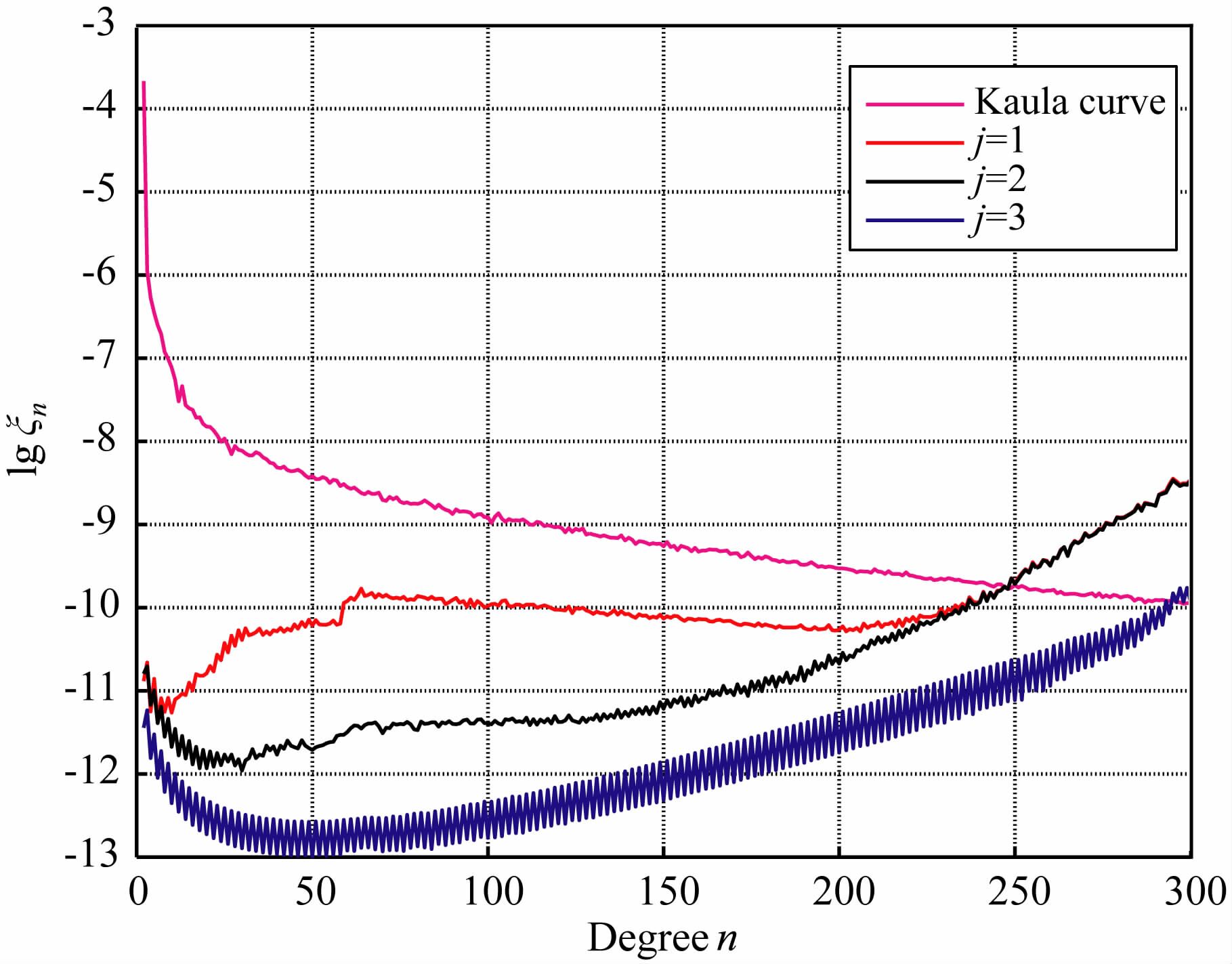
称为vj对v的n阶逼近阶方差,其图解通常简称逼近阶方差.根据公式(17)和(18)可知,Kaula曲线描述了位系数随着阶数n的变化情况,而逼近阶方差则刻画了两个调和函数位系数的近似程度.
|
图 1 恢复的引力场位系数的阶方差 Fig. 1 The degree deviation distributions for recovered coefficients |
从图 1可知,若对轨道上引力梯度不进行归算(j=1的情况),则还原位系数的阶数达到250阶;进行了一次归算后(j=2的情况),虽然位系数恢复阶数仍维持在250 阶左右,但系数的计算精度比j=1时有明显提高;二次归算后(j=3的情况)恢复位系数的阶数不仅达到了300 阶,而且系数的计算精度有进一步的提高.
不断增加归算次数对提高引力场位系数的恢复精度有一定的影响,但这并不意味着处理实际GOCE 数据时归算次数越多就能将地球重力场或者引力场求解得越精确,其原因在于实测的引力梯度数据存在着一定的误差,该误差是无法通过归算等手段消除掉的,属于GOCE 观测的固有误差.
4 结论与说明本文基于Taylor展开公式提出了将卫星轨道上引力梯度不变量扰动归算到相应平均球面上的方法,并利用EGM2008 模型对上述归算方法以及位系数恢复进行了模拟计算,结果表明,经过一次归算基本上能达到GOCE 引力梯度的观测精度(3mE).但是考虑到计算误差等原因,建议对GOCE 实际观测数据时做两次循环归算.
为了计算方便,本文将卫星轨道面取成了椭球面.尽管实际的GOCE 轨道面比椭球面要复杂,但本文计算中所取的延拓距离比GOCE 实际轨道的相应距离要大3 倍左右,因此本文结论对处理GOCE 数据是成立的.理由是延拓的精度主要取决于延拓的距离.
尽管本文没有处理实际的GOCE 数据,但进行模拟归算或计算是十分必要的.因为只有在数值模拟的情况下才能正确评估归算或计算精度,以及对建立的理论方法进行验证.从所得的结果看,本文提出的归算方法是可以用于实际GOCE 数据处理的.
| [1] | Bouman J, Koop R, Tscherning C C. Calibration of GOCE SGG data using high-low SST, terrestrial gravity data and global gravity field models. Journal of Geodesy , 2004, 78(1-2): 124-137. |
| [2] | Bouman J, Rispens S, Gruber T, et al. Preprocessing of gravity gradients at the GOCE high-level processing facility. Journal of Geodesy , 2009, 83(7): 659-678. DOI:10.1007/s00190-008-0279-9 |
| [3] | Muzi D, Allasio A. GOCE: the first core Earth explorer of ESA's Earth observation program. Acta Astronautica , 2004, 54(3): 167-175. DOI:10.1016/S0094-5765(02)00296-5 |
| [4] | Visser P, Van den IJssel J, Van Helleputte T, et al. Orbit determination for the GOCE satellite. Advances in Space Research , 2009, 43(5): 760-768. DOI:10.1016/j.asr.2008.09.016 |
| [5] | Eshagh M, Abdollahzadeh M. The Effect of Geopotential Perturbations of Goce on Its Observations—a Numerical Study. Acta Geodaetica Et Geophysica Hungarica , 2009, 44(4): 385-398. DOI:10.1556/AGeod.44.2009.4.2 |
| [6] | Bettadpur S V, Schutz B E, Lundberg J B. Spherical harmonic synthesis and least-squares computations in satellite gravity gradiometry. Bulletin Geodesique , 1992, 66(3): 261-271. DOI:10.1007/BF02033186 |
| [7] | Klees R, Koop R, Visser P, et al. Efficient gravity field recovery from GOCE gravity gradient observations. Journal of Geodesy , 2000, 74(7-8): 561-571. DOI:10.1007/s001900000118 |
| [8] | Milani A, Rossi A, Villani D. A timewise kinematic method for satellite gradiometry: GOCE simulations. Earth Moon and Planets , 2005, 97(1-2): 37-68. |
| [9] | Pail R, Plank G. Assessment of three numerical solution strategies for gravity field recovery from GOCE satellite gravity gradiometry implemented on parallel platform. Journal of Geodesy , 2002, 76: 462-474. DOI:10.1007/s00190-002-0277-2 |
| [10] | Ditmar P, Kusche J, Klees R. Computation of spherical harmonic coefficients from gravity gradiometry data to be acquired by the GOCE satellite: Regularization issues. Journal of Geodesy , 2003, 77: 465. DOI:10.1007/s00190-003-0349-y |
| [11] | Petrovskaya M S, Vershkov A N. Non-singular expressions for the gravity gradients in the local north-oriented and orbital reference frames. Journal of Geodesy , 2006, 80: 117-127. DOI:10.1007/s00190-006-0031-2 |
| [12] | 吴星, 张传定. 卫星重力梯度分量的广义轮胎调和分析. 测绘学报 , 2009, 38: 101–107. Wu X, Zhang C D. Generalized torus harmonic analysis of satellite gravity gradients component. Acta Geodaetica et Cartographica Sinica (in Chinese) , 2009, 38: 101-107. |
| [13] | Cunderlik R, Mikula K, Mojzes M. Numerical solution of the linearized fixed gravimetric boundary-value problem. Journal of Geodesy , 2008, 82(1): 15-29. DOI:10.1007/s00190-007-0154-0 |
| [14] | Yu Jinhai, Zhao Dongming. The gravitational gradient tensor's invariants and the related boundary conditions. Sci China Earth Sci (Ser-D) , 2010, 53: 781-790. DOI:10.1007/s11430-010-0014-2 |
| [15] | Baur O, Sneeuw S, Grafarend E W. Methodology and use of tensor invariants for satellite gravity gradiometry. Journal of Geodesy , 2008, 82: 279-293. DOI:10.1007/s00190-007-0178-5 |
| [16] | 于锦海, 万晓云. 计算Legendre函数导数的非奇异方法. 测绘科学技术学报 , 2010, 27(1): 1–3. Yu J H, Wan X Y. Non-Singular Formulae for Computing Derivatives of Legendre Functions. Journal of Geomatics Science and Technology (in Chinese) , 2010, 27(1): 1-3. |
 2011, Vol. 54
2011, Vol. 54