2. 桂林理工大学地球科学学院,桂林 5410042
2. College of Earth Sciences,Guilin University of Technology,Guilin 541004 , China
近年国内外都很重视对坑道超前预报方法技术的研究,陆续有新方法和新设备应用于生产实践中.目前主要应用的物探超前预报方法有TSP 法、地质雷达法、陆地声纳法、直流电阻率法、红外探测法、瑞雷波法等.这些方法都取得了较好的效果[1-3].由于探测装置自身与勘探环境的限制,坑道中电法勘探工作总是会受到坑道体本身和坑道壁旁侧的干扰,有时会严重影响成果资料的解释.针对坑道特殊观测条件下存在的局限性,阮百尧等[4]在已有研究成果基础上,提出全新直流聚焦超前探测方法,该方法在掌子面和坑道上布设屏蔽电极来约束主探测电极的电流,使其电场分布主要集中在屏蔽电流所围成的区域前方,很大程度上降低了掌子面后方坑道本身及侧壁对电流分布的影响.
早在20世纪50年代,有研究将直流电法用于煤矿井下探测[5].目前坑道中直流电法超前探测技术主要是在原三极测深基础上改进、发展而来的.从最初的单点源法发展到两点源法,再到目前的三点源法[6-9].电法超前探测技术属于“非接触式"探测,具有高效、方便、廉价的特点.目前直流电阻率超前探测技术已大量应用于井下巷道前方(含侧方)未知地质构造灾害的探测中.
利用数值方法对点源地电场进行三维模拟国内外已有许多工作[10-12],并取得了实质性进展,方法技术相对较成熟.目前国内对坑道直流聚焦超前探测方法技术的研究较少.阮百尧等[4]利用二维轴对称模型对坑道条件下环状电极布设方式的聚焦超前探测原理及效果进行了分析研究,但是只能模拟简单模型,对于复杂地质环境下聚焦装置的探测效果研究不够.强建科等[13]用有限元方法着重模拟分析了三维坑道条件下聚焦超前探测几种电极组合的空间电位分布特征,同样对于复杂环境下异常探测效果未进行分析,未涉及坑道旁侧异常体的探测问题.综合分析地面垂向测深和侧向测井装置特点,笔者设计出适用于坑道掌子面和坑道侧壁勘探的垂直聚焦超前探测方案.为了检验方案的可行性,本文采用有限元技术进行数值模拟计算,应用压缩存储技术对大型稀疏刚度矩阵进行高效存储,结合预条件的迭代方法求解大型稀疏、对称的线性方程组,大幅提高了计算效率.通过与全空间坑道掌子面电位垂直聚焦探测解析解、土槽物理模拟试验结果及数值模型计算结果对比分析,说明垂直聚焦超前探测方案能够正确探查坑道掘进面前方及坑道侧壁附近有害地质体的分布与存在.
2 坑道垂直聚焦超前探测装置学者A.N 查博罗夫斯基首先提出同性点源装置的垂向聚焦测深法,该方法包括电位观测方案(AMA′)和梯度观测方案(AMNA′),主要在地表勘探中使用.后H.Л.格里果里耶娃用梯度装置对良导球体上的视电阻率异常进行系统计算[14];20世纪60-70 年代先后有多篇同性源装置相关研究与应用的学术论文发表[15-18].我国学者在20世纪80年代和90年代初期也对地表同性点源的垂向测深方法技术进行了研究论证,并应用于实际生产中,取得较好的效果[19-21].
20世纪70年代,我国在电测井工作中引入侧向测井方案解决钻孔生产工作中的实际问题.侧向测井方案分为三侧向测井、七侧向测井、微侧向测井和微球形聚焦测井等[22].各种方案均以同性源的相斥特性及约束聚焦原理为前提,电极设计中采用监督电极、屏蔽电极和主电极的不同组合来达到强制约束电流在井中目标层位定向、定位分布的目的.
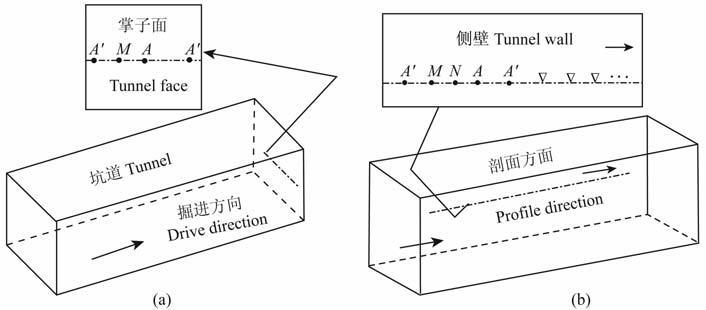
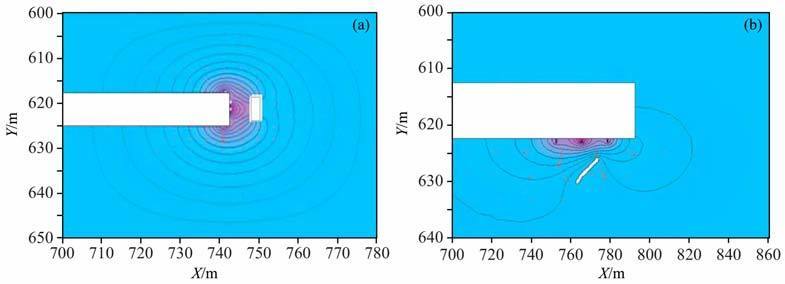
本文根据阮百尧提出的直流聚焦超前探测原理,结合前人在地表垂向测深和侧向测井工作中应用的同性电极对工作装置,设计出适用于坑道掌子面及侧壁的垂直聚焦超前探测方案.分为坑道掌子面和侧壁垂直聚焦超前探测方案(如图 1所示):(1)掌子面电位测量方案(A′MAA′装置或A′AMA′装置),由屏蔽电极、主电极和测量电极组成,通过调节屏蔽电极的屏蔽作用,约束主电极产生的电流,减少旁侧的影响,使其在介质中“定向"传播,从而实现聚焦的效果.该装置适用于布设在掌子面上探测掘进面前方的不良地质存在.也可以根据实际需要在屏蔽电极外侧对称于主电极的位置上分别布设两个稳定电极,形成A″A′MAA′A″ 装置或A″A′AMA′A″装置,以此来加强屏蔽电极对主电极发射电流的约束作用;(2)侧壁及底板梯度测量方案(A′MNAA′装置或A′AMNA′ 装置),由于沿着坑道走向进行剖面测量,相对于掌子面观测沿坑道中轴线空间较大,故设计电位梯度观测方案,全空间中坑道本身对测量结果造成的影响在一定程度上可以视作系统误差,测量电极直接采集对称于主电极两边的屏蔽电极约束作用下的主电极聚焦电场分布.本文主要讨论的是由屏蔽电极、主电极和测量电极组成的观测装置的探测效能.工作时根据需要布设好探测装置,屏蔽电极A′ 和主电极A输出的都是同性正电流,测量电极M或MN位于主电极和屏蔽电极轴线上,负极回路B置于巷道外无穷远处.通过调整屏蔽电极和主电极输出电流强度的大小,来改变屏蔽电极约束下主探测电极电流场分布.图 2a所示为掌子面前方存在一低阻体时直流垂直聚焦场的分布特征,图 2b为坑道旁侧存在一走向延长与坑道斜交低阻体时剖面探测装置垂直聚焦场的分布特征,两图中所取均为同一深度Z=110m 时电场水平分布特征.
|
图 1 坑道垂直聚焦装置(a)掌子面电位观测方案(b)侧壁剖面梯度观测方案 Fig. 1 Tunnel vertical focusing device (a) face potential detection mode and(b) profile gradient detection mode |
|
图 2 直流聚焦装置掌子面观测(a)与侧壁剖面观测(b)电场分布水平切面图 Fig. 2 Transverse plane cross-section view of potential and electric field distribution offocus arrangement on the tunnel face (a) on the tunnel wall (b) |
在坑道中进行直流聚焦探测,通常忽略地表与空气界面的影响,假设坑道环境下的电场为全空间分布.设电流为I的点电源P产生的直流场电位为u,σ为介质的电导率,σ′ 为介质的异常电导率(σ′=σ-σ0),σ0为电源点处电导率.则全空间中任一点产生的异常电位u满足如下微分方程[23]:
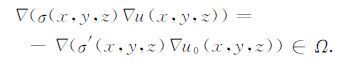
|
(1) |
数值模拟过程中,为了减少计算工作量,在满足计算需要的前提下人为给定一个无穷远边界Γ∞ ,针对本文设计的垂直聚焦超前探测装置,其边界上电场分布如下:
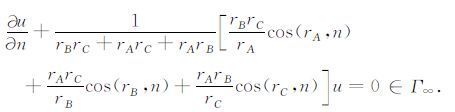
|
(2) |
其中,n为边界外法线方向,rA,rB和rC是源点到测量点的距离,cos(rA,n)是某点边界外法线方向的单位矢量n和rA夹角的余弦,cos(rB,n)和cos(rC,n)同理.
与上述边值问题等价的垂直聚焦三点源异常电位变分问题为
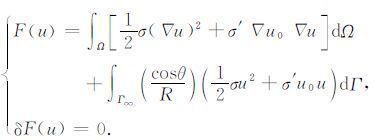
|
(3) |
(3) 式中边界相关积分项表示为
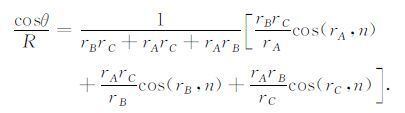
|
(4) |
为了更好地模拟复杂地质条件和不规则异常体对研究区域Ω 采用四面体单元进行剖分,每个子单元e中对四个顶点电位采用线性插值,详细说明见文献[24, 25].
用有限单元法对(3)式异常电位变分问题求解,将研究区域Ω 和边界Γ∞ 的积分分解为各子单元e和Γe上某个节点的信息,进一步扩展成全体节点组成的矩阵或列阵,最后整合叠加所有单元节点信息Fe(u)就得到该变分问题在整个区域Ω 上的积分:
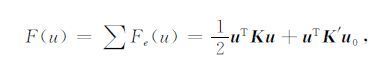
|
(5) |
令(5)式的变分为零,得线性方程组:
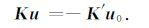
|
(6) |
方程组(6)的解即为各节点异常电位u,K和K′为系数矩阵,u0 为正常电位向量.
3.3 刚度矩阵存储及线性方程组求解经有限元方法离散后,各单元刚度矩阵集成的总刚度矩阵为大型稀疏矩阵,采用改进的行压缩存储方式MSR(Modified Sparse Row)将合成的总刚度矩阵存储到两个一维数组中.对包含大量离散地电模型单元信息的对称正定线性方程组采用矩阵分裂型SSOR(Symmetric Successive Over Relaxation)预条件的共轭梯度迭代方法进行高效求解[26].构造预条件矩阵PSSOR为
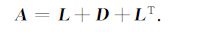
|
(7) |
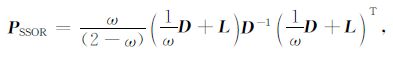
|
(8) |
其中,L为严格下三角阵,D为对角阵,ω 为松弛因子(0<ω <2).注意到当取ω =1得到SGS(Guass-Seidel)预条件矩阵的构造形式,经试算本文模拟计算中,取ω =1.6效果最佳.
本文预条件的共轭梯度法迭代过程如下[16]:
给定初值x0,计算初始残量:
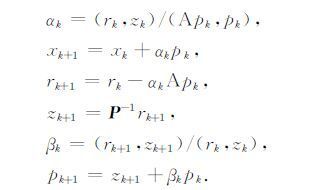
|
DO k=0,1,2,…,n,进行迭代:
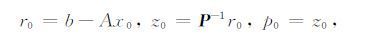
|
ENDDO.收敛条件判断:满足要求则停止,否则继续迭代.
预条件矩阵的结构直接决定收敛的效果,构造出一个有效的预条件矩阵应满足以下特征:
(1) P为对称正定矩阵;(2)P应保持与A一样的稀疏特征;(3)P的构造应具有如(8)式所示的特殊结构;(4)P-1A的特征值分布要集中.
4 聚焦装置总电位计算坑道中作业空间有限,电极均布设在掌子面和侧壁上,为了减少源点对其附近拟合场的影响,采用异常电位进行计算.异常电位计算的总电位包括点电源在均匀空间中产生的正常电位u0 和不均匀体产生的异常电位u两部分.正常电位u0 由解析公式u0 =Iρ0/ωR求出,此处ω 是某点源对研究区域Ω 张的立体角,坑道全空间取值为4π,R为观测点到源点的空间距离.对于主要操作面在掌子面上的直流聚焦超前探测装置来说,坑道空腔对于迎头前方异常响应的影响相对侧壁的影响较小[27].为了使模拟计算更符合实际,文中设计所有模型坑道空腔电阻率为108 Ωm, 将坑道影响一并带入计算.垂直聚焦超前探测装置,掌子面及侧壁上探测电极与屏蔽电极在均匀全空间中产生的正常电位为
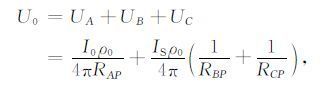
|
(9) |
RAP,RBP,RCP分别为A,B,C三个极点到空间任一节点P的距离,ρ0 为源点处电阻率,本文选取供给主电极的电流I0 与屏蔽电极的屏蔽电流IS 之比为1.A为主电极,B、C为对称排列在A的两边的屏蔽电极.
异常电位u的求解按照前述有限元数值计算步骤,通过求解稀疏线性方程组得到.
5 计算结果分析 5.1 全空间垂直聚焦场电位分布模型为均匀全空间中一掘进坑道中,采用如图1a所示掌子面垂直聚焦电位装置A′MAA′ 进行超前探测模拟.根据公式(9)计算求取掌子面前方异常电位分布的解析解.如图 3a所示,设计坑道掘进面尺寸为7 m×7 m, 主电极A位于掌子面四角对角线中心,屏蔽电极对称布设于主电极两边,屏蔽电极间距6m, 测量电极位置距离主电极1 m.全空间电阻率为ρ0=100Ωm.供电后一次求取出测量电极M前方一定距离内每隔2m 的电位分布特征,对比掌子面上探测电极前方坑道空腔存在条件下电位分布的数值解和解析解,验证本程序计算的正确性.从电位对比分析曲线图 3b可以看出,除了第一个点存在较大的误差外(相对误差约为13%左右),其余各点数值解与解析解吻合较好,误差满足计算所需精度要求.分析认为造成第一个点误差较大的原因是解析解为全空间均匀场介质计算得出,数值模拟时考虑了坑道的影响,所以在模型计算结果离坑道最近的第一个点受坑道腔体影响,其值与无坑道条件下的解析解误差较大.
|
图 3 有限元模拟精度分析 (a)均匀全空间坑道模型水平切片;(b)数值解与解析解结果比较. Fig. 3 Accuracy analysis of finite element simulation (a) slices oftunnel model in ■,(b) The comparison of numerical and analytical solution. |
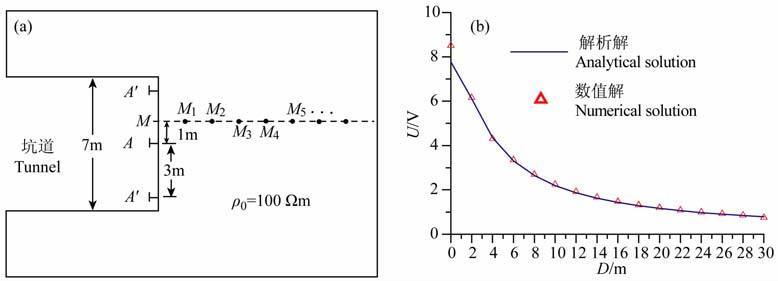
土槽物理模拟以粘土作为传导介质,土槽长150cm, 宽120cm, 高80cm.采用半空间镜像法模拟研究全空间坑道掌子面聚焦探测效果.如图 4a所示,设计模型坑道宽度B=14cm, 半高H=7cm.异常体用铜板模拟,铜板边长R分别为15cm 和10cm, 厚度S=0.4cm.经测量铜板电阻率为0.01Ωm, 粘土平均电阻率为60Ωm.以相同的参数设置,采用垂直聚焦电位测量装置对土槽试验模型进行数值模拟,测量结果如图 4b所示.图中D表示掘进面到异常的距离,纵坐标为归一化的测量值与背景值的比值.
|
图 4 (a)土槽物理模拟装置及(b)数值模拟与物理模拟结果对比 Fig. 4 Clay physical model device (a) and compare of numerical modeling and soilbox testing result (b) |
由于土槽中模型介质为人工条件下预置,与理论要求的均一介质存在差距,为了使曲线更好比较,图 4b中数值模拟与土槽实验的结果采用归一化的电位曲线表示,结果显示有限元数值模拟结果基本与土槽实际情况吻合.尽管曲线尾支下降段出现局部不重合现象,但并不影响两条曲线在总体形态和趋势上的一致性.同等参数设置下的土槽物理模拟实验与数值模型计算的结果对比,说明本文讨论的坑道垂直聚焦超前探测方案可行,模拟计算结果可靠,能够有效反映出掘进前方一定探测范围内异常体的存在.
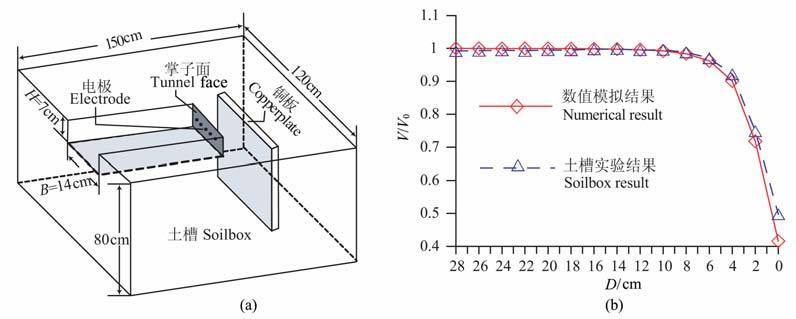
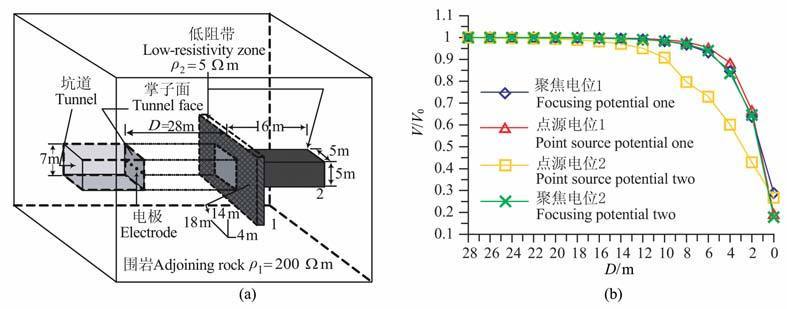
6 算例 6.1 模型一如图 5a所示,该模型为坑道掘进面前方存在一低阻带,分别采用掌子面垂直聚焦电位装置和无屏蔽电极约束的单点源电位测量装置,通过计算屏蔽电极存在与否所得到的观测结果来对比两种不同装置的探测效果.模型中测量电极布设位置固定为主探测电极一侧距离1m 处.设计模型坑道掘进面尺寸7m×7m, 到破碎带的掘进距离为28m, 围岩电阻率ρ1=200Ωm, 破碎带电阻率ρ2=5Ωm.破碎带尺寸及与坑道的位置关系分别为:(1)破碎带尺寸18m×14m×4m 坑道掌子面沿掘进方向垂直投影在破碎带中心;(2)破碎带尺寸5m×5m×16m, 其中心轴与坑道中轴重合,纵切面水平投影位于坑道掌子面内部.
|
图 5 掘进面前方低阻破碎带模型计算结果 (a)低阻破碎带模型;(b)聚焦装置与单点源测量结果.D为掘进面到低阻带的距离,纵坐标为归一化的电位测量结果. Fig. 5 Model of Low-resistivity fracture zone ahead the heading and computational results (a)Model of Low-resistivity fracture zone;b) Potential curves of shielded focus survey and point source survey. |
本模型针对掌子面聚焦电位装置和掌子面单点源电位测量进行模拟计算,结果如图 5b所示.观察1号低阻异常的聚焦电位曲线和单点源电位曲线,在供电电流相同的前提下,可看到聚焦电位归一化异常下降幅度大于单点源电位测量归一化曲线的下降幅度;2 号低阻异常的归一化聚焦电位曲线和单点源电位曲线中,聚焦探测装置对于前方低阻带的探测距离和异常响应能力明显优于单点源电位测量,聚焦电位归一化曲线在掘进面距离低阻带还有16m 的位置开始下降,在距离低阻带10 m 位置曲线下降明显;单点源装置电位曲线在距离破碎带8m的位置才开始下降.对比1 号和2 号低阻异常的归一化曲线可以看到,两条单点源电位的测量结果基本没有太大的变化,说明无屏蔽电极存在的单点电位对不同异常的区分能力较差;由于1 号异常的尺寸相对于掌子面尺寸很大,而且掌子面中心位置和异常中心重合,测量时低阻电流场较强,导致聚焦装置对1 号异常的反应没有2 号异常的那么明显.从理论上讲,点源场电位为三维等势球面分布,因此坑道中对异常体响应方位的判断存在缺陷,而且异常位置不规则时,坑道及掌子面本身对单点源测量结果的影响相对于带屏蔽电极的聚焦装置要大.
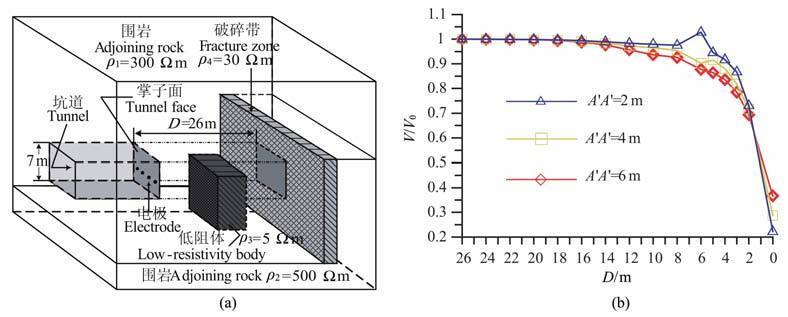
6.2 模型二该模型模拟垂直构造破碎接触带及低阻干扰条件下的聚焦超前探测效果,网格剖分为60×30×30个单元.如图 6a所示,掘进面(7m×7m)前方为一低阻接触带,厚3m, 电阻率ρ4=30Ωm, 接触带两侧围岩电阻率分别为ρ1=300Ωm, ρ2=500Ωm.在巷道旁侧存在一含水低阻异常体(4m×11m×3m),电阻率ρ3=5Ωm, 与巷道侧壁间隔1m, 沿掘进方向距低阻破碎带距离为3 m, 模型设计如图 6a示意.采用如图 1a所示装置在掌子面上布极,两侧屏蔽电极极距A′A′ 分别设计为2m、4m 和6m, 主电极位于两屏蔽电极连线中点,探测电极布设于主电极与屏蔽电极连线任一侧,距离主电极1m且位置固定.
|
图 6 两层介质中旁侧干扰组合模型计算结果 (a)两层介质组合模型;(b)不同聚焦极距计算结果.D为掌子面到异常的掘进距离,纵坐标为归一化电位. Fig. 6 Computational resules of combined model with side distrubance in two layers (a) Combined model in two layers, (b) Computational results of normalized potential curve with different focusing electrode spacing. |
分析图 6b中曲线可以看出在距离模拟破碎带16m 处曲线开始下降趋势,随着挖掘工作前进在距离缩短到8 m 的位置上,曲线整体下降的趋势明显.在距离模拟破碎带6-4m 的位置上曲线出现小幅异常上扬同时保持总体下降趋势,此区间为经过旁侧低阻异常体位置.当屏蔽电极距A′A′=4m 时,在掘进面离低阻破碎带6 m 位置刚到达旁侧低阻异常位置,此处归一化电位出现高点突变,分析认为屏蔽电极距与掌子面尺寸相比较小(为坑道边长的1/3),聚焦电场的分布较易受到坑道本身顶角及侧壁和掌子面交界处突变的影响.尤其在旁侧低阻存在时,造成聚焦场电流密度在旁侧低阻体的吸引下沿着掌子面和侧壁与掌子面交界立面局部加强,最后导致探测电极和屏蔽电极间测量到的电位增高.因此在工作中设计屏蔽电极距时应尽量使其接近掌子面边界尺寸.可见垂直聚焦装置可以在一定程度上反映出旁侧低阻隐患的存在,同时不影响对掘进面前方主探测区的探测效果.模型计算表明,在掌子面尺寸范围内,屏蔽电极极距越大对前方及坑道旁侧异常体的探测效果越好,这与文献[12]中二维轴对称模拟计算得出的结论一致.
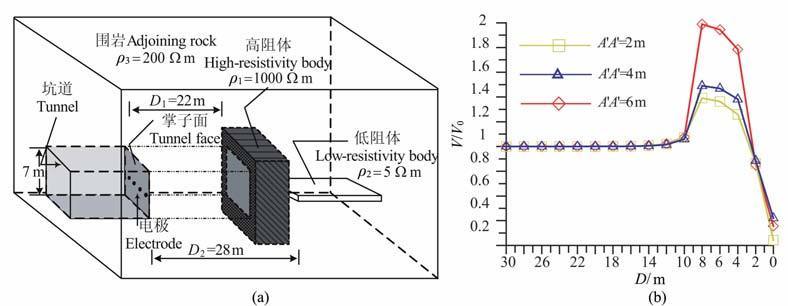
6.3 模型三本模型模拟高阻屏蔽条件下对低阻包体的探测效果,同样网格剖分为60×30×30 个单元.设计坑道掘进面(7m×7m)前方分别存在一个高阻板状屏蔽体(10m×10m×6m)和一个低阻体(10 m×2m×20 m),高阻体电阻率为ρ1=1000Ωm, 低阻体电阻率为ρ2=5Ωm, 围岩电阻率ρ3=200Ωm(图7a).设置模型掘进距离到高阻体为D1=22m, 到低阻体为D2=30 m, 高阻体穿越厚度为6 m.屏蔽电极极距A′A′设计为2m、4m 和6m, 主电极位于两屏蔽电极连线中点位置.
图 7b横坐标为掘进面到异常的距离,纵坐标为归一化电位,从特征曲线上可以看出,随着掘进工作的进行,曲线在横坐标14m 的位置开始上升,此位置距离高阻体8m;在横坐标8m位置达到正幅值,此处横坐标位置对应围岩与高阻模型接触面;从此接触面开始,随着挖掘工作进入高阻介质,受到前方6m 处低阻包体的影响,归一化电位曲线开始明显下降,通过高阻体后在距离低阻异常还有2m 时在高阻体对电流的“排斥"和前方低阻体对电流的“吸引"作用下曲线下降幅度已远远超出正常背景,据此可以作出前方存在低阻异常的判断.出现上述情况是由直流电场的特性所决定,高阻体具有“阻碍"电流通过的作用,因此接近其附近时测得电位很高;相反低阻体“吸引"电流,在其附近测量电位时表现出的是低场值.模型计算可以看出随着屏蔽电极距的增大,高阻异常的幅值相应增大,低阻异常的幅值相应减小.
|
图 7 掌子面垂直聚焦探测模型计算结果 (a)高阻屏蔽模型;(b)不同聚焦极距计算结果. Fig. 7 Computational results of model with vertical focus detection on tunnel face (a) Model with Iligh-resistivity body shielded; (b) Results of normalized potential curve with different focusing electrode spacing. |
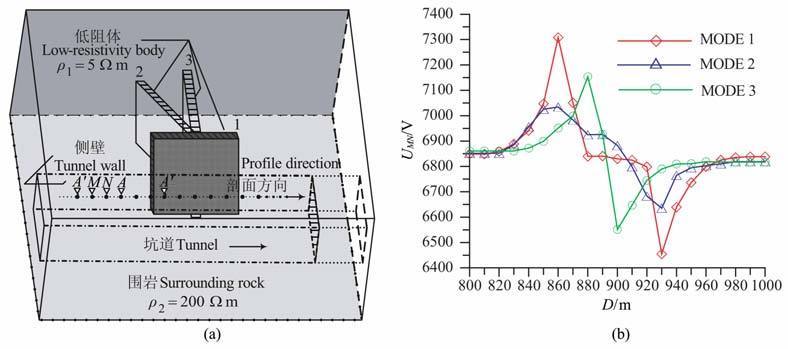
设计坑道掘进面尺寸为7m×7m, 距离掌子面100m 处的坑道旁侧存在一低阻板状体,模型尺寸为60m×20m×10m.低阻体长边平面与坑道侧壁测量平面的位置分别为垂直、水平和斜交(设计模型编号分别为3、1和2),与坑道测量侧壁最近端距离为2m.低阻体设计电阻率为ρ1=5Ωm, 围岩电阻率ρ2 =200 Ωm.采用设计的垂直聚焦梯度剖面A′AMNA′ 装置测量,设计工作剖面点距5m;两端屏蔽电极A′A′ 间极距为50m, 主电极A位于其中点;测量电极MN极距10m, 记录点距离主电极10m;测量剖面长度为200 m, 设计不同有限走向低阻体位于剖面中段,图 8a为模型空间位置示意图.剖面测量结果如图 8b 所示,图中纵坐标表示MN电极间电位差,横坐标为剖面测线长度,从图中可看出设计梯度装置剖面测量能够较好地反映出坑道旁侧不同产状和走向的低阻体与坑道走向的位置关系.当低阻板状体走向与坑道侧壁平行时(编号1 位置),梯度电位异常的最高值和最低值分别出现在测量电极进入和离开低阻板状体的边界位置,在低阻板状体的中间部位,梯度电位变化较小;当低阻板状体延伸方向与坑道斜交时(编号2 位置),梯度电位异常幅值仍然出现在板状体两个延伸端的边界位置,与平行走向不同的是,异常边界过度较圆滑,而且经过板状体中间部位时,异常变化幅度随着测点离板状体的近侧壁端投影距离的的接近而变大,相对于低阻薄板远端引起的异常,近端异常边界更明显;当低阻板状体走向与坑道侧壁垂直时(编号3 位置),梯度电位曲线最高值与最低值中点即为剖面所经过板状体的中心位置,幅值位置很好的反映出了低阻板状体的边界异常.其中图 8a中曲线图例编号与图8b中低阻体模型编号对应.
|
图 8 坑道垂直聚焦梯度剖面探测模型计算结果 (a)坑道旁侧低阻模型;(b)剖面梯度电位计算结果. Fig. 8 Computational results of model with vertically focused gradient protile survey tn tunnel (a) Low-resistivity model beside tunnel wall ;(b)The curves of gradient potential on profile. |
(1) 深入分析地面电阻率垂向测深技术和直流侧向测井技术,在已有研究基础上设计出适用于坑道掌子面和侧壁剖面测量的直流垂直聚焦超前探测电位观测方案.应用有限元数值模拟三维坑道环境下直流聚焦超前探测方案的勘探效果.通过与全空间坑道模型解析解和土槽物理模拟结果对比,说明文中的垂直聚焦探测方案能够准确探测出坑道掌子面前方及坑道旁侧不良地质体的存在及空间分布.
(2) 高效地改进行压缩存储模式及预条件共轭梯度算法的应用,大大提高程序的运算效率.可实现坑道三维环境下针对掘进面前方和坑道侧壁旁侧不良地质体直流聚焦超前探测响应的快速模拟研究.
(3) 掌子面和侧壁探测装置的模型计算表明设计的垂直聚焦超前探测方案能够有效的探测掘进面前方一定距离内存在的不良地质体,能够识别和排除旁侧异常对掘进面前方异常的干扰;剖面探测装置能够很好地反映坑道体旁侧不良地质隐患与坑道的空间位置及延伸关系.今后应设计和模拟更多适合巷道条件下的观测方案,使得该探测技术更加完善.结合更多数值模拟和物理模拟实验,对巷道施工中常见地质条件下的探测环境进行模拟研究,为该方法技术的发展及应用提供丰富的理论支持及模型参考.
| [1] | 王爱平. 八字岭隧道超前地质预报. 铁道建筑技术 , 2005, 4: 49–52. Wang A P. Advance geological forecast technology of Baziling Tunnel. Railway Construction Technology (in Chinese) , 2005, 4: 49-52. |
| [2] | 谭金龙, 陈耀蝉, 刘基. 瞬态面波勘探技术在隧道超前预报中的应用. 土工基础 , 2005, 19(4): 86–90. Tan J L, Chen Y C, Liu J. Application of transient surface wave exploration technology for forecast in tunnel engineering. Soii Eng.and Foundation (in Chinese) , 2005, 19(4): 86-90. |
| [3] | 李丽华. 地下声波法CT探测技术在工程地质勘查中的应用. 工程勘察 , 2002, 6: 60–62. Ll L H. Application of the subsurface sonic CT technique in engineering geological exploration. Geotechnical Investigation & Surveying (in Chinese) , 2002, 6: 60-62. |
| [4] | 阮百尧, 邓小康, 刘海飞, 等. 坑道直流电阻率超前聚焦探测新方法研究. 地球物理学报 , 2009, 52(1): 289–296. Ruan B Y, Deng X K, Liu H F, et al. Research on a new method of advanced focus detection with DC resistivity in tunnel. Chinese J. Geophys. (in Chinese) , 2009, 52(1): 289-296. |
| [5] | 王齐仁.隧道地质灾害超前探测方法研究.长沙:中南大学信息物理工程学院,2008 |
| [6] | 李玉宝. 矿井电法超前探测技术. 煤炭科学技术 , 2002, 30(2): 1–3. Ll Y B. Mine electric method pilot detection technology. Coal Science and Technique (in Chinese) , 2002, 30(2): 1-3. |
| [7] | 髙致宏, 闫述, 王秀臣, 等. 巷道超前(电法)探测的应用现状与存在的问题. 煤炭技术 , 2006, 25(5): 120–121. |
| [8] | 程久龙, 王玉和, 于师建, 等. 巷道掘进中电阻率法超前探测原理与应用. 煤田地质与勘探 , 2000, 28(4): 60–62. Cheng J L, Wang Y H, Yu S J, et al. The principle and application of advance surveying in roadway excavation by resistivity method. Coal Geology & Exploration (in Chinese) , 2000, 28(4): 60-62. |
| [9] | 刘青雯. 井下电法超前探测方法及其应用. 煤田地质与勘探 , 2001, 29(5): 60–62. Liu Q W. Underground electrical lead survey method and its application. Coal Geology & Exploration (in Chinese) , 2001, 29(5): 60-62. |
| [10] | 阮百尧, 熊彬, 徐世浙. 三维地电断面电阻率测深有限元数值模拟. 地球科学 , 2001, 26(1): 73–77. Ruan B Y, Xiong B, Xu S Z. Finite element method for modelingresistivity sounding 32D geo2electric section. Earth Science Journal of China University of Geoscience (in Chinese) , 2001, 26(1): 73-77. |
| [11] | Dey A, Morrison H F. Resistivity modeling for arbitrarily shaped three-dimensional structures. Geophysics , 1979, 4(44): 753-780. |
| [12] | Holcomble H T, Jirack GR. Three-dimensional terrain correction in resistivity surveys. Gophysics , 1984, 49: 33-5. |
| [13] | 强建科, 阮百尧, 周俊杰. 三维坑道直流聚焦法超前探测的电极组合研究. 地球物理学报 , 2010, 53(3): 695–699. Qiang J K, Ruan B Y, Zhou J J. Reaearch on the array of electrodes of advanced focus detection with 3D DC resistivity in tunnel. Chinese J .Geophys. (in Chinese) , 2010, 53(3): 695-699. |
| [14] | H L Grigorova. Comparision of ρk Anomaly on the Conducting Sphere with Various Array of DC Electric. Beijing : Geological Publishing House , 1954. |
| [15] | Ravindra N. Gupta, Hattacharya P K.Unipole method of electrical profiling. Gophysics , 1963, 28(4): 608-616. DOI:10.1190/1.1439236 |
| [16] | Roy A, Apparao A. Depth of investigation in direct current methods. Gophysics , 1971, 36(5): 943-959. DOI:10.1190/1.1440226 |
| [17] | Abhijit Dey etl. Electric field response of Two-Dimensional inhomogeneities to unipolar and bipolar electriode configurations. Geophysics , 1975, 40(4): 630-640. DOI:10.1190/1.1440554 |
| [18] | Brizzolarl E, Bernabini M Comparison between Schlumberger electrode arrangement and some focused electrode arrangements in resistivity profiles.1979,27:223-244 |
| [19] | 黄启声. 垂向屏障等位电测法. 物探与化探 , 1981(3): 164–171. Huang Q S. Vertical shield isopotential electric survey. Geophysical and Geochemical Exploration (in Chinese) , 1981(3): 164-171. |
| [20] | 费锡铨. 聚焦垂直极化法. 地质与勘探 , 1983(10): 46–50. FeiX Q. Method of focused vertical polarization. Geology and Prospecting (in Chinese) , 1983(10): 46-50. |
| [21] | 梁鋈廷. 三电极系侧向测井的径向几何因子. 地球物理学报 , 1975, 18(4): 284–296. Liang XT. The radial geometric factors for the three electrode laterologging. Chinese J .Geophys. (in Chinese) , 1975, 18(4): 284-296. |
| [22] | 张庚骥主编. 电法测井-上册. 北京: 石油工业出版社, 1984 : 83 -127. Zhang G J. Electrical Logging (in Chinese) ( Volume Ⅰ) (in Chinese). Beijing: Petroleum lndustry Press, 1984 : 83 -127. |
| [23] | 徐世浙. 地球物理中的有限单元法. 北京: 科学出版社, 1994 : 178 -188. Xu S Z. The Finite Element Method in Geophysics (in Chinese). Beijing: Science Press, 1994 : 178 -188. |
| [24] | 《MathHandbook》Compile Group. Math Handbook . Beijing: Higher Education Press, 1979 : 993 -994. |
| [25] | Kattan P I. MATLAB Guide to Finite Elements. Translated by Han L B.Beijing: Tsinghua University Press, 2004 : 287 -315. |
| [26] | Yousef Saad. tterative Methods for Sparse Linear Systems. Beijing: Science Press, 2009 : 261 -288. |
| [27] | 黄俊革, 王家林, 阮百尧. 坑道直流电阻率法超前探测研究. 地球物理学报 , 2006, 49(5): 1529–1538. Huang J G, Wang J L, Ruan BY. A study on advanced detection using DC resistivity method in tunnel. Chinese J .Geophys. (in Chinese) , 2006, 49(5): 1529-1538. |
 2011, Vol. 55
2011, Vol. 55

