在地球物理电磁法模拟中需要计算含有振荡贝塞尔函数的Hankel积分,尤其是在基于积分方程技术的三维电磁场计算中,异常场被表示为异常电偶极子源产生的场的叠加,其格林函数就是Hankel积分[1].由于贝塞尔函数的高震荡性,传统上多采用数字滤波方法计算该积分[2-4].当核函数单调、快速衰减、且收发距不是很大时,数字滤波能取得较好的结果[5].但是电磁法中遇到的大部分核函数并不衰减或者衰减很慢,这给应用数字滤波技术带来了困难.为此,一般从两个方面入手,一是对核函数进行改进,比如朴化荣[5],汤井田[6]用具有解析结果的半空间模型核函数对格林函数核函数进行修正.另一方面,采用高精度数字滤波技术进行计算,但数字滤波器具有方法依赖性,且高精度滤波器一般很长,计算量较大.Chave[7]给出了计算这种积分的直接积分计算方法,并且应用连分式来加快收敛的速度.翁爱华等[8]将该方法应用到可控源音频大地电磁测深一维正演中,取得较好的效果.汤井田[9]提出将核函数修正后再利用直接积分方法计算的方法.直接积分法具有较高的计算精度,而且不需要核函数,具有很好的性质,但是由于直接积分法是在每两个零点之间都进行积分,需要较长的计算时间.
Fang等[10]提出了一种基于Somefeld积分公式计算此类积分的方法,称为离散复镜像法(Discrete complex image method, 简称DCIM),其思想是首先将核函数近似为一系列的幂指数级数,然后利用Somefeld积分公式将Hankel积分转换为多项式的求和.该方法避免了繁琐的积分过程,且不要求核函数收敛,具有较高的计算效率.
离散复镜像法的关键问题是核函数的近似.Chow 等[11]最早利用Prony方法来实现核函数的近似,但是Prony方法抗干扰性差[12],而且需要提取准静态项和表面波项[13].为了克服Prony方法的缺点,Hua等[14]提出了广义函数束方法(Generalized pencil-of-function, 简称GPOF),提高了核函数近似的抗干扰性,且在不需要提取准静态项和表面波项的情况下就可以取得精确的近似.Aksun[12]在广义函数束方法的基础上进一步给出了二级近似的方法,实现了利用较少的采样点即可实现核函数的精确估计,大大提高离散复镜像法的计算速度.Ge等[13]将二级近似的广义函数束方法应用到Hankel积分计算当中,给出了新的解形式.
离散复镜像法主要应用于天线波场和微带结构等的高频电磁场计算中.虽然在地球物理领域,徐利明等[15]提出利用离散复镜像法实现了埋地目标体矢量散射的快速正演;邵长金等[16]利用基于广义函数束方法的一级近似离散复镜像法实现了垂直磁偶极子的矢量势和标量势的计算.但更高精度的二级近似离散复镜像法在低频电磁勘探理论计算中还没有应用,而且目前的近似参数也是针对高频电磁格林函数计算提出,在电磁法勘探这种低频的电磁场计算中尚不适用.因此,本文将研究二级近似的离散复镜像法在地球物理电磁法模拟中的应用,并通过数值计算分析,提出了在低频电磁场中应用二级近似的离散复镜像法时近似参数的选取原则.
2 方法理论 2.1 离散复镜像法在地球物理电磁场计算中,需要计算大量的Hankel积分,
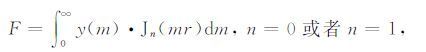
|
(1) |
其中Jn为第一类的第n阶Bessel函数;y(m)为谱域格林函数,也被称为核函数.
如果将谱域格林函数y(m)展开成复指数级数,即
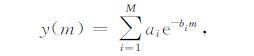
|
(2) |
其中ai和bi为与模型参数有关的待定系数,M为拟合的多项式个数,则应用Lipschitz-Somefeld 恒等式
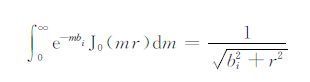
|
(3) |
和
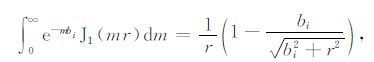
|
(4) |
可以得到(1)式的闭式解为[13]

|
(5) |
公式(5)中多项式的每一项都可以看成是离散后的一个镜像,ai是幅度,1/ $\sqrt {b_i^2 + {r^2}} $ 和(1-bi/ $\sqrt {b_i^2 + {r^2}} $/r是镜像位置,并且由于它们都是复数,所以这种方法被称为离散复镜像法[10].另外,从公式(5)还可以看出,待定系数只和模型参数有关;如果模型不变,则ai和bi保持不变,此时闭式的解只和源与接收点几何位置有关系.这样,同层中只需要计算一次该系数,就可以应用到所有位置格林函数的计算中,从而可以大大提高计算效率.
2.2 基于广义函数束方法的二级近似技术离散复镜像法的关键技术是如何求取公式(5)中的待定系数ai和bi.利用广义函数束方法计算这些待定系数的原理是通过求矩阵的特征值来代替用最小二乘法直接求超定方程组,具体原理见附录A.
由于在核函数变化剧烈的地方需要很小的采样间隔来实现精确近似,而广义函数束方法又是基于等间隔采样的方法,如果全区间都使用同样的采样间隔近似的话,核函数采样数将非常大.为此,采用二级近似技术,将核函数变化剧烈的地方划为一个区间,其余地方为另一个区间,使用不同的采样间隔,这样可同时提高计算效率和近似精度.具体说来,首先取有限积分区间[0,L2]来替代无穷积分区间[0,∞).然后,将[0,L2]区间根据核函数变化率的不同进一步分隔为[0,L1]和[L1,L2]两个子区间,并且在这两个区间内对核函数进行N2 和N1 个等间隔采样.在此基础上,对核函数y(m)在子区间[L1,L2]上应用广义函数束方法近似,结果记为F1.显然,[L1,L2]子区间近似的F1 并不能在全区间[0,L2]上近似核函数,特别是在子区间[0,L1]中.所以在子区间[0,L1]上再对核函数近似误差y(m)-F1进一步应用广义函数束方法近似,结果记为F2.因此,F2 实际上是对F1 在区间[0,L1]上近似的纠正项.这样,Hankel积分可以写为[10]
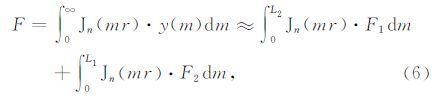
|
(6) |
式中,n=0或者1.同理可以推导出三级近似,四级近似等等.上式中的每一个积分都可以利用离散复镜像法计算.
将(6)式写成离散形式,有
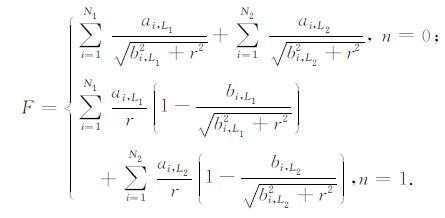
|
(7) |
其中ai,L1、biL,1、ai,L2和bi,L2为核函数在区间L1 和L2 的近似系数.从(7)式可见,二级近似方法的精度取决于参数N1、N2、L1 和L2.下面针对在低频电磁场计算中如何选择这些参数进行讨论.
3 近似参数选取 3.1 N1 和N2 的确定N1 和N2 的选取与函数的变化率有关:变化剧烈的地方需要较密的采样点;变化平缓的地方较稀疏的采样点即可满足要求.理论上来说,N1 和N2的值越大对核函数的拟合越精确,但是我们希望用较少的采样来实现核函数的拟合.由于广义函数束方法对其求解过程中应用的参数L的限制,即要求L满足M<L<N-M(见附录A),使得N1 和N2 不能小于2×(M+1),M为近似多项式个数.M的值越大越能精确地拟合核函数,但是取大的M就会带来更多的未知系数,给求解带来更大的计算量.在保证足够精度的情况下,M越小越好,袁建生等[17]提出M取4或5即可满足需要,本文通过模拟,认为取4就可以满足要求.在确定了N1 和N2 的取值下限后,对于附录B中的核函数,通过不断增加N1 和N2 的值进行核函数拟合来寻找合适的N1 和N2,最终确定N1 和N2 控制在10×M左右即可.
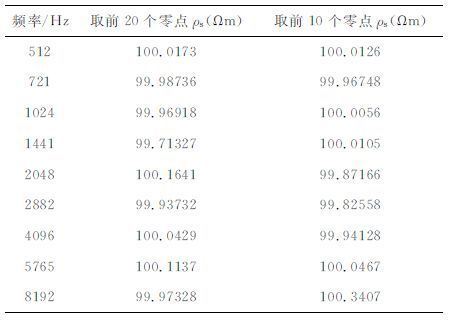
3.2 L2 的选取Ge等[13]认为最合适的L2 应使核函数y(m)满足y(L2)<ε,这里ε是一个非常小的数,小于ε的值在积分时可以忽略.但是在地球物理应用中,核函数在很大范围内往往都是单调递增的[5],无法衰减到ε,所以Ge等提出的方法不合适.但由于贝塞尔函数是震荡衰减的,所以可以通过贝塞尔函数的性质来截断积分区间.表 1 以100Ωm 均匀大地表面的电偶极子阻抗视电阻率为例,给出了取贝塞尔函数的前10个零点和前20 个零点计算结果,比较发现发现2组数据相差很小,考虑到计算效率,取前10 个零点为积分区间即可满足精度要求.由于不论0 阶还是1阶贝塞尔函数的前10 个零点都在40 以内,所以积分变量m的上限L2 的大小可以用收发距离r归一化取为40/r.因为阻抗视电阻率涉及电场和磁场,因此该例子适用于电性源格林函数计算.
|
|
表 1 取贝塞尔函数前20个零点与前10个零点视电阻率结果 Table 1 Apparent resistivity using the first 20 and 10 zero points of Bessel function |
L1 的选取非常关键,对近似结果影响很大.Aksun[12]给出了根据模型最大的层介电常数来确定L1 办法,但是本文的研究是准静态近似条件下的电磁场,不考虑层介电常数影响,所以该方法不合适.Ge等[13]只指出要求L1<L2,并未给出具体的取值办法.本文通过研究,认为可以按照

|
(8) |
确定L1.因此,如何确定最合适的Q是确定L1 的关键.
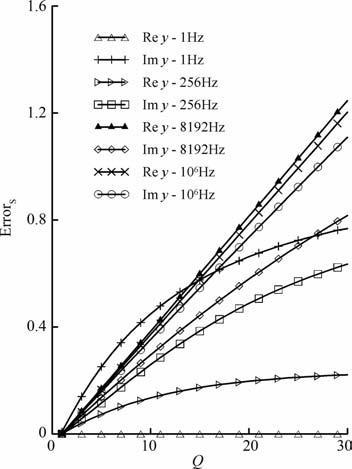
以三层模型为例,电阻率分别为100、200Ωm 和300Ωm, 前两层厚度均为100m.应用二级近似技术对附录B中的核函数y(m)=m/(m+n1/R*)进行近似,图 1为m=2×10-3时Q值对核函数的近似的影响情况,误差计算采用errors =.(yGPOF -yexact)/yexact.,GPOF 为拟合解,exact为精确解.从图 1中可以看出,随Q值增大核函数的近似误差增大,在低频时,误差先随Q增加线性增加,然后趋于饱和;但随频率增高实部和虚部的误差随Q线性增加.
|
图 1 不同频率的核函数近似误差曲线(L2=4×10-3,N1=50,N2=50) Fig. 1 Dependence of approximation error of kernel function on different frequency (L2=4×10-3,N1=50,N2=50) |
这样就提供了一个最佳Q值求取的简便算法,即在计算开始时选用高频求出2 个不同Q值时的近似误差,然后计算出该误差曲线的方程,从而能求出曲线与横轴的交点,该点即为合适的Q值.通过试验,对于附录B 中的三个核函数,Q基本相同,都接近1.
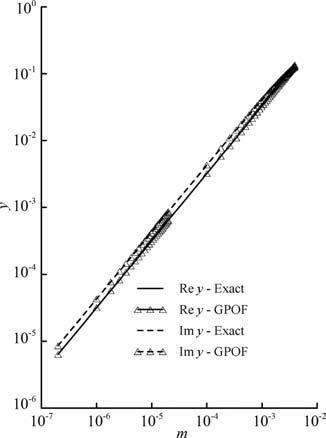
实际上,确定Q以后,无论如何改变L2 和N1,只要按照公式(8)来求取L1,近似精度不受影响.为了说明此问题,还是对于图 1中的核函数,在确定出Q=1后,保持Q不变,分别通过改变L2 和N1 来改变L1,研究其近似精度变化,结果见图 2和图 3.图2给出了将积分区间L1 和L2 扩大100倍后的核函数的近似情况,从图可见,积分区间扩大后,核函数性质发生了较明显的变化,由单调增加在大变量时变为近水平的饱和曲线.尽管如此,近似计算的精度没有明显变化.图 3 为保持L2 的大小不变,将N1取值由50变200时的近似结果.从图可见,采用最优的Q,改变N1 虽然改变了L1 的大小,但是并不会影响近似的精度.

|
图 2 改变L1 和L2 的范围对核函数近似的影响(N1=50,N2=50,Q=1) Fig. 2 Impact of range of Li and L2 on the approximationof kernel function(N1=50,N2=50,Q=1) |
|
图 3 改变N1 对核函数近似的影响(L2=4×10-3,N2=50,Q=1) Fig. 3 Impact of Ni on the approximation of kernel function (L2=4×10-3,N2=50,Q=1) |
作为上面近似参数选择的具体应用,我们对电磁法勘探中目前常用的双极源可控源音频大地电磁测深的电磁场进行了数值计算.有限长双极源频率域电磁场表达式见附录B[18].这里设收发距为8000m, 供电电流为10A.为了对比,采用用直接数值积分法结果和离散复镜像法进行对比的方法.
4.1 均匀半空间情形设均匀半空电阻率为100Ωm, 应用离散复镜像法的参数为:L2=4×10-3,L1=8×10-5,N1=50,N2=50,Q=1.图 4a为直接积分法和离散复镜像法计算的均匀半空间的卡尼亚视电阻率.从图可见,视电阻率曲线在1-10 Hz处为-45°下降曲线,从10Hz往后开始进入远区,视电阻率曲线变为一水平直线,并接近真实电阻率100Ωm.由于低频时场进入近区,计算卡尼亚视电阻率不能反映介质真电阻率,故采用高于128Hz的高频段比较两种方法的计算误差(图 4b),采用误差公式为error=.(ρs-ρ)/ρ.×100%.从图 4b可以看出来,直接积分法的误差随频率的增加逐渐增大,而离散复镜像法的误差保持在0.5%以下,充分反映了介质的真电阻率.

|
图 4 均匀半空间直接积分法与离散复镜像法得到的视电阻率计算结果及误差变化(ρ=100Ωm)(a)视电阻率;(b)相对误差. Fig. 4 Apparent resisitivity (a) computing from the results of direct integration method and DCIM on a 100 Hm half space model and the relative error (b) from actual resistivity |
为了验证近似参数的稳定性和有效性,利用与图 4中相同装置和近似参数,分别计算了三层模型与四层模型的模型响应.
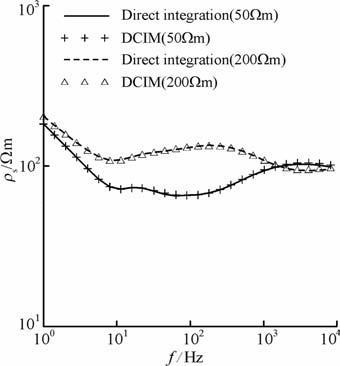
4.2.1 三层模型三层模型的前两层厚度均为100 m, 第一层和第三层电阻率均为100Ωm.第二层电阻率分别为50Ωm 和200Ωm, 图 5给出了视电阻率计算结果.从图中可以看出,针对这两种中间层电阻率不同模型,直接数值积分与离散复镜像法结果吻合很好.在低频时,由于近场效应,视电阻率不反映地层真电阻率.但随着频率增加,在10-1000Hz范围内的视电阻率曲线基本反映了中间层与深部地层的电阻率变化.图 5说明近似参数独立于模型参数,具有一定普适性.
|
图 5 三层模型的视电阻率曲线(中间层电阻率分别取50Ωm 和200Ωm) Fig. 5 Apparent resistivity curves of three-layered models (resistivity of intermediate layer is 50 Ωm and 200 Ωm respectively) |
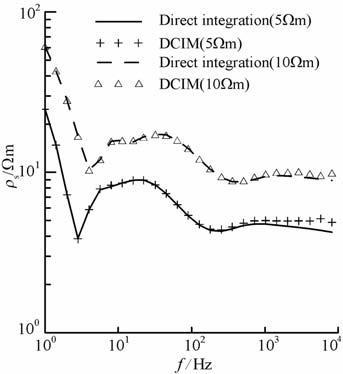
四层模型的前三层厚度分别为100、200m和300m, 第二层和第四层电阻率均为100Ωm.第一层与第三层电阻率为5Ωm 以及10Ωm 时的卡尼亚视电阻率计算结果见图 6.从图 6中可以看出,直接数值积分法与离散复镜像法在大部分频率范围内都吻合很好,只是在高频部分结果不同.对于高频部分,卡尼亚视电阻率反应第一层的电阻率,此时模型近似为均匀半空间.与4.1 节均匀半空间的情形相同,离散复镜像的结果与第一层电阻率吻合较好,而直接数值积分法误差较大.图 6 中的结果进一步说明文中提出的近似参数不受模型参数的限制,可以应用到各种模型计算中.
|
图 6 四层模型的视电阻率曲线(第一层和第三层电阻率分别取为5Ωm 和10Ωm) Fig. 6 Apparent resistivity curve of four-layered model (resistivity of the first layer and the third layer is 5 Ωm and 10 Ωm respectively) |
基于广义函数束方法的二级近似技术是一种高效率、高精度的Hankel积分计算方法,其最终解的形式可以大大提高大规模格林函数的计算效率.本文将该方法推广到低频电磁场计算中,并给出了具体的近似参数的选取方法:(1)N1 和N2 取值在10×M左右,M为近似多项式的个数,一般取4 即可;(2)L2 取为40/r,r为收发距;(3)L1=Q×(L2/N1),0<Q<N1,Q的最优值根据谱格林函数拟合相对误差随Q值变化的近似误差曲线与横轴的交点来确定.
通过对有限长双极源的不同模型的电磁场进行模拟,表明本文提出的离散复镜像法近似参数及选取原则是合理可行的,并可应用到其他电磁方法的电磁场计算中.
附录A 广义函数束方法原理令${y_k} = \sum\limits_{i = 1}^M {{a_i}{e^{{b_i}\delta tk}}} $,这里k=0,1,…,N-1,N为采样个数,M为近似用的多项式的个数,一般4项就可以达到需要的精度,δt为采样间隔.令zi=exp(biδt),代表在Z平面的极点.
存在如下的向量
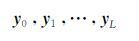
|
其中
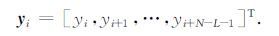
|
定义矩阵

|
为了了解这两个矩阵的底层结构,将其写成

|
(A1) |
其中

|
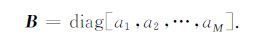
|
(A2) |
基于上面的分解,如果M≤L≤ N-M,极点{zi;i=1,2,…,M}是矩阵束Y2 -zY1 的广义特征值.当L=M的时候,这种方法就退化为普通的函数束方法,这里更关心的是M<L< N-M时的值.
为了说明计算矩阵束的广义特征值的方法,写出如下表达式:
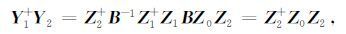
|
(A3) |
这里上角标+代表伪逆,“-1"代表逆.从公式(A3)可以看出存在向量{pi;i=1,2,…,M}使得
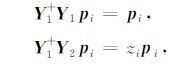
|
(A4) |
这里pi是矩阵束Y2 -zY1 的广义特征向量.
为了计算伪逆Y1+ ,可以利用Y1 的奇异值分解:
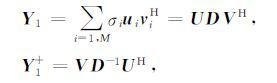
|
(A5) |
这里U= [u1,u2,…,uM],V= [v1,…,vM],D=diag[σ1,…,σM].上角标H 代表共轭转置.U和V是左右的奇异值向量矩阵.对于含有噪声的数据yk,可以选择σ1,…,σM为Y1 的M个最大的奇异值,这样求出来的Y1+ 被称为Y1 的截断的伪逆.
因为Y1+Y1 =VVH,并且VHV=I,将公式(5)带入到公式(4)中,并将公式(4)左乘VH 得到
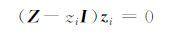
|
其中i=1,2,…,M,
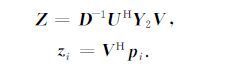
|
这里Z是M×M的矩阵,zi和zi分别是矩阵Z的特征值和特征向量.这里求出zi后可进一步求出bi,然后利用最小二乘法计算出ai.
附录B 双极源电磁场表达式设长导线源AB长度为2L,供电电流强度为I,则电场x方向和磁场y方向的场强表达式为

|
(B1) |
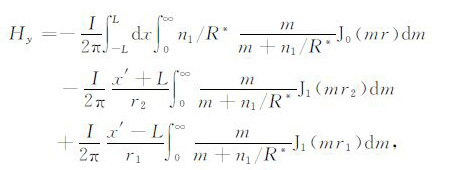
|
(B2) |
其中(x',y')是要计算点的坐标;(x,y)是长导线源AB中点的坐标;m为积分变量;${n_j} = \sqrt {{m^2} - k_j^2} ,k_j^2 = - i\omega {\mu _0}{\sigma _j}$,kj是第j个电性层的波数,σj是第j个电性层的电导率;${r_1} = \sqrt {{{\left( {{x^\prime } - L} \right)}^2} + {y^{\prime2}}} ,{r_2} = \sqrt {{{\left( {{x^\prime } + L} \right)}^2} + {y^{\prime2}}} $;
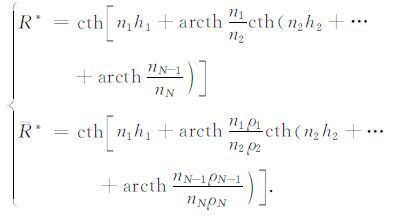
|
(B3) |
卡尼亚视电阻率公式为
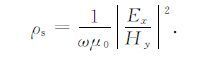
|
(B4) |
| [1] | Wannamaker P E, Hohmann G W, SanFilipo W A. Electromagnetic modeling of three-dimensional bodies in layered earths using integral equations. Geophysics , 1984, 49(1): 60-74. DOI:10.1190/1.1441562 |
| [2] | Ghosh P P. The application of linear filter theory to the direct integration of geoelectrical resistivity sounding measurements. Geophysical Prospecting , 1971, 19(2): 192-217. DOI:10.1111/gpr.1971.19.issue-2 |
| [3] | Anderson W L. Numerical integration of related Hankel transforms of orders 0 and 1 by adaptive digital filtering. Geophysics , 1979, 44(10): 1287-1305. |
| [4] | 罗延钟, 张胜业, 王卫平. 时间域航空电磁法一维正演研究. 地球物理学报 , 2003, 46(5): 719–724. Luo Y Z, Zhang S Y, Wang W P. A research on one-dimension forward for aerial electromagnetic method in time domain. Chinese J.Geophys (in Chinese) , 2003, 46(5): 719-724. |
| [5] | 朴化荣. 电磁测深法原理. 北京: 地质出版社, 1990 . Piao H R. Principles of Electromagnetic Soundings (in Chinese). Beijing: Geological Publishing House, 1990 . |
| [6] | 汤井田, 何继善. 可控源音频大地电磁法及其应用. 湖南: 中南大学出版社, 2005 . Tang J T, He J S. Controllable Source Audio Magnetotelluric Method and Its Application (in Chinese). Hunan: Central South University Press, 2005 . |
| [7] | Chave A D. Numerical integration of related Hankel transforms by quadrature and continued fraction expansion. Geophysics , 1982, 48(12): 1671-1686. |
| [8] | 翁爱华, 王雪秋. 利用数值积分提高一维模型电偶源电磁测深响应计算精度. 西北地震学报 , 2003, 25(3): 193–197. Weng A H, Wang X Q. Utilizing direct integration to enhance calculation accuracy of 1D electromagnetic response for current dipole source. Northwestern Seismological Journal (in Chinese) , 2003, 25(3): 193-197. |
| [9] | 汤井田, 罗维斌, 刘长生. 海底油气藏地质模型的冲击响应. 地球物理学报 , 2008, 51(6): 1929–1935. Tang J T, Luo W B, Liu C S. Impulse response of seafloor hydrocarbon reservoir model. Chinese J. Geophys (in Chinese) , 2008, 51(6): 1929-1935. |
| [10] | Fang D G, Yang J J, Delisle G Y. Discrete image theory for horizontal electric dipoles in a multilayered medium. Proc.Inst.Elect.Eng , 1988, 135(10): 297-303. |
| [11] | Chow Y L, Yang J J, Fang D G, Howard G E. A closed-form spatial Green's function for the thick microstrip substrate. IEEE Trans.Microwave.Theory Tech , 1991, 39(3): 588-592. DOI:10.1109/22.75309 |
| [12] | Aksun M I. A robust approach for the derivation of closed-form Green's functions. IEEE Trans.Microwave.Theory Tech , 1996, 44(5): 651-658. DOI:10.1109/22.493917 |
| [13] | Ge Y H, Esselle K P. New closed-form Green's functions for microstrip structures-theory and results. IEEE Trans.Microwave.Theory Tech , 2002, 50(6): 1556-1560. DOI:10.1109/TMTT.2002.1006417 |
| [14] | Hua Y, Sarkar T K. Generalized pencil-of-function method for extracting poles of an EM system from its transient response. IEEE Trans. on Antennas Propaga , 1989, 37(2): 229-234. DOI:10.1109/8.18710 |
| [15] | 徐利明, 聂在平. 埋地目标体矢量电磁散射的一种快速正演算法. 地球物理学报 , 2005, 48(1): 209–215. Xu L M, Nie Z P. A fast forward algorithm for modeling vector electromagnetic scattering from buried dielectric objects. Chinese J. Geophys (in Chinese) , 2005, 48(1): 209-215. |
| [16] | 邵长金, 李相方. 离散复镜像法求取层状介质的格林函数. 中国石油大学学报(自然科学版) , 2006, 30(1): 150–153. Shao C J, Li X F. Calculation of spatial-domain Green's functions for multi-layered media by discrete complex image method. Journal of China University of Petroleum (in Chinese) , 2006, 30(1): 150-153. |
| [17] | 袁建生, 李中新. 求解多层媒质中点源电场问题的复镜像法. 清华大学学报(自然科学版) , 1999, 39(5): 51–53. Yuan J S, Li Z X. Complex image method for calculating electrostatic field in multilayer media. J Tsinghua Univ (Sci&Tech) (in Chinese) , 1999, 39(5): 51-53. |
| [18] | 殷长春. 可控源音频磁大地电流法一维正演及精度评价. 长春地质学院学报 , 1994, 24(4): 438–443. Yin C C. One-dimensional modeling of CSAMT method and evaluation of calculation precision. Journal of Changchun University of Earth Sciences (in Chinese) , 1994, 24(4): 438-443. |
 2011, Vol. 54
2011, Vol. 54