2. 中国石油化工股份有限公司胜利油田分公司物探研究院,东营 257061;
3. 中国石油杭州地质研究院,杭州 310023
2. Geophysical Research Institute of SINOPEC Shengli Oilfield, Dongying 257061, China;
3. Petro China Research Institute of Geology, Hangzhou 310023, China
在地震数据处理中,多次波通常作为噪音被压制和消除,并且已经发展了很多衰减多次波的方法.这些衰减多次波的方法主要分为两大类,一类是建立在一次波和多次波在周期性、速度或者动校正量等特征存在差异的基础上,在不同变换域中滤除多次波的滤波方法[1-4].这类方法用于一些复杂构造的多次波衰减时,可能会遇到多次波和一次波之间的特征差异很小或是没有差异的情况,这时这类滤波方法适用的前提条件得不到满足,方法的应用效果就可能会大打折扣.另一类是基于波动方程的预测相减法,这种方法的思路是先预测出多次,然后将其从地震记录中有效地减去[5-8].这类方法能适用于复杂的地下构造,难点在于预测的多次波和原始记录中多次波的精确匹配.因此要将多次波从原始记录中彻底消除,多次波衰减的方法还有很大的提升空间.
事实上,多次波并不是绝对地只能被当做噪音来处理.和一次波类似,多次波是地下反射层的多次波反射,因此也蕴含了地下反射界面的信息,在复杂的地质条件下,甚至包含了一次反射波不具有的地下信息.因此,很多地球物理学家从不同角度尝试不同的方法利用多次波进行成像[9].
Reiter等[10]提出利用叠前Kirchhoff方法对深海多次波进行成像.Sheng[11]以及Yu和Schuster[12]应用互相关偏移的思路对多次波进行成像.Berkhout和Verschuur[13]以及Guitton[14]利用组合炮偏移的方法对多次波进行成像.除此之外,Shan[15] 以及Berkhout和Verschuur[16]先将多次波转化成准一次波,然后再对准一次波进行成像.这些方法都能够成功实现利用多次波信息对地下构造的准确成像,但是他们都是单独对多次波和一次波进行成像,因此,需要一次波和多次波进行分离,而且,多次波的偏移结果和一次波的偏移结果的合成也不是通过简单叠加就能实现的.
因此也有很多学者尝试将多次波和一次波同时成像.Youn和Zhou[17]提出基于双程弹性波动方程对一次波和多次波同时进行成像.这种方法实现的精度高,但是前提是需要高精确的速度场,方法实现涉及到庞大的存储和计算量,并且需要较好的后续的滤波方法来滤除双程波偏移结果中的偏移噪声.Brown[18]以及Brown 和Guitton[19]应用最小二乘联合成像方法实现多次波和一次波的联合成像.这种方法利用时差特征构建成像算子,因此方法的精度在复杂地质条件下受到了限制.Muijs等[20]提出对多次波和一次波进行叠前深度偏移.这种方法首先将海底电缆观测到的数据进行下行波和上行波场分离,分离出的下行波和上行波在偏移过程中分别用于多次波成像的震源和接收记录;然后利用常规波场延拓的方法并基于2D 反褶积成像条件进行成像;这种方法比较适用于海底电缆观测数据,而且,成像前必须将数据进行上、下行波场的成功分离,也为方法的实施增加了工作量和制约条件.
本文基于广义概念上的炮偏移成像算法,对常规一次波偏移成像方法从用于向下延拓的上、下行场以及成像条件方面分别进行了改进,来实现表层多次波和一次波联合成像.
2 常规一次波炮偏移对于常规一次反射波叠前深度偏移,基于共炮集的波动方程叠前深度偏移的基本思路是,首先对每一炮进行单炮偏移成像,然后再把各炮成像结果在对应地下位置上叠加,从而得到整个成像剖面.对于每一炮,标准的波动方程叠前深度偏移总体上包括两大步:第一步是上、下行波的波场深度延拓,即将震源波场在时间的正方向上向下延拓和将震源激发产生的记录波场沿时间的反方向向下延拓;第二步是应用成像原理,提取每一个深度层位上的成像值[21].
以“相关成像条件"为例,上述思路可用式(1)表示:
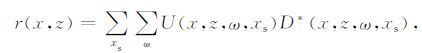
|
(1) |
其中,ω 是频率;xs 表示震源点坐标;U(x,z,ω,xs)和D(x,z,ω,xs)分别表示震源点在xs 处的上、下行波场延拓至地下(x,z)处的频率域波场值;D* (x,z,ω,xs)表示波场D(x,z,ω,xs)的共轭复数;r(x,z)表示成像点(x,z)处的成像结果.
根据式(1)所示成像条件提取成像值的原则是,延拓至反射层位的上、下行波场需满足频率域的零延迟互相关,即下行波场与上行波场的到达时间相同.
3 表层多次波和一次波联合成像 3.1 表层多次波和一次波联合成像方法的基本原理本文中表层多次波和一次波联合成像的方法与上述一次反射波的成像思路类似,都是先进行上、下行波的波场深度延拓,再应用成像原理,提取每一个深度层位上的成像值.不同的是用于延拓的上、下行波场和所应用的成像条件.图 1 展示了利用各阶表层多次波进行成像的基本原理.
|
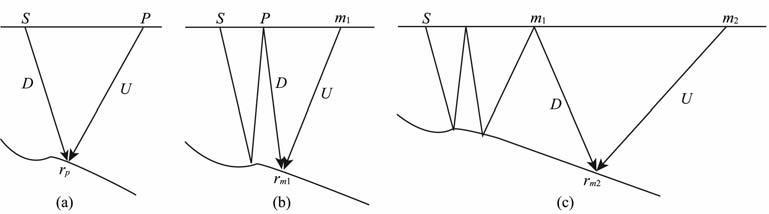
图 1 表层多次波和一次波成像示意图 (a)利用一次波(零阶多次波)成像原理示意图;(b)利用一阶表层多次波进行成像原理示意图;(c)利用二阶表层多次波进行成像示意图. Fig. 1 Illustration of imaging with surface-related multiples and primaries (a) Illustration of imaging with primary (zero order multiple) ; (b) Illustration of imaging with first-order multiple; (c) Illustration of imaging with second-order multiple. |
图 1a中将震源点S处的震源波场信息和P点接收的一次波(或称零阶表层多次波)向下延拓,基于反射成像条件即可对rp 点成像;图 1b中S为震源点,P点接收到一次波,m1 点接收到一阶表层多次波,此一阶表层多次波是P点的一次波继续向下传播经反射层再反射回来的波场.则P点接收的一次波可看作m1 点的一阶表层多次波的拟震源,将P点的一次波和m1 点的一阶表层多次波分别向下延拓,并应用成像条件即可获取rm1 点的成像值;在图1c中,将m1 点接收到的一阶表层多次波当作m2 点接收到的二阶表层多次波的拟震源,同时将m1 点的一阶表层多次波和m2 点的二阶表层多次波向下延拓,应用成像条件即可对rm2 点进行成像;同理,只要相应的拟震源波场信息包含在向下延拓的震源波场中,任意阶的多次波都可以成像.
3.2 表层多次波和一次波联合成像所应用的震源和接收波场在只对一次波进行偏移时,通常用脉冲震源波场作为一次反射波的下行震源波场.在以下的篇幅中,我们将应用脉冲震源波场作为下行震源波场和应用公式(1)所示成像条件来获取成像结果的方法,称为常规偏移方法.
根据上述表层多次波和一次波联合偏移成像的基本原理,上述常规偏移方法不再适用于对含有多次波的记录进行成像.原因在于,脉冲震源只是一次波的震源,因此,只含有脉冲震源的震源波场中不包含表层多次波的震源信息,无法实现对多次波成像;
本文中表层多次波和一次波同时进行成像的方法,是将含有表层多次波的原始记录和脉冲震源之和用于向下延拓的下行震源波场,含有表层多次波的接收记录用于逆向延拓的接收波场.则对于接收波场记录中的n阶多次波,其震源波场,即n-1阶多次波必然包含在由整个波场记录和脉冲震源组成的震源波场记录中,其中一次波的震源波场为脉冲震源信息.那么,在偏移过程中,利用成对的n-1阶多次波震源信息和n阶多次波接收记录就可以实现对n(n≥0)阶多次波的偏移成像(将一次波看作零阶多次波),成像原理如3.1 所述,即可实现表层多次波和一次波联合成像.
3.3 表层多次波和一次波联合成像基于的波场延拓算法为适应复杂的地质构造成像,也为了后续成像条件的使用,本文中应用带误差补偿的频率空间域有限差分波场延拓算子来实现波场延拓.它的处理包含了三步:频率-空间域的有限差分处理,频率-空间域的时移处理,频率-波数域的误差补偿处理,这种算法补偿了频率-空间域有限差分法求解时引入的误差,对介质速度横向变化剧烈的地区也有很好的适应性.这种算法的详细推导见参考文献[22],在此不再赘述.
3.4 表层多次波和一次波联合成像所基于的成像条件根据3.2部分所述,和常规一次波偏移方法不同,表层多次波和一次波联合成像方法所用的震源波场信息来自于实际接收记录的复杂波场和脉冲震源之和,而非简单的脉冲震源波场,则常规1D 相关成像条件不再适用.
根据常规成像方法所用的如方程(1)所示的1D相关成像条件,只要延拓的上、下行波场的能量相遇即可构建出成像值,这种成像条件对于将脉冲震源用作下行震源波场的一次波成像是适用的,但是若用于本文中将整个含有多次波的记录和脉冲震源之和作为震源波场的成像方法,则会引入很强的成像噪音,影响成像效果,原理如图 2所示:
|
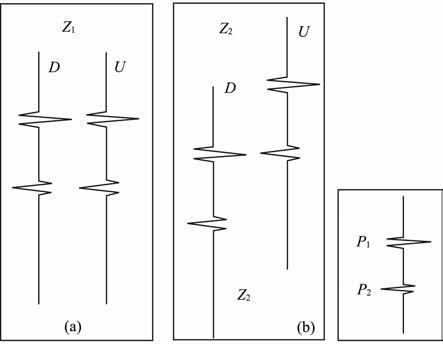
图 2 常规1D 相关成像条件用于含有多次波记录成像引起成像噪音的原因 Fig. 2 Illustration of the origin of crosstalk noise using one-dimensional crosscorrelation imaging condition for imaging with multiples |
在图 2中,震源波场包含如图 2右下角所示的两个脉冲能量P1 和P2 ,分别代表一次波和多次波能量.则在地下只有单反射层Z1 的背景下,接收波场也只包含这两个脉冲能量P1 和P2 .用D和U分别表示向下延拓的震源波场和接收波场.在图 2a中,D和U同时延拓至真正反射层Z1 ,波场D中的P1 和P2 与U中的P1 和P2 分别对应相遇,根据1D 相关成像条件,可以构建出正确的反射成像值;图 2a中波场D和U分别继续延拓至深度Z2 ,如图2b所示,Z2 处没有真正的反射点,但是,由于波场的复杂性,波场D中的能量P1 与U中的P2 相遇,根据1D 相关成像条件,此处仍然可以构建出成像值.但是由于D中的P1 与U中的P2 不是来对应同一震源的能量,因此由它们构建出来的成像结果是假的,表现为成像结果中的噪音.
随着成像条件的改进和发展,也出现了不同于式(1)所示的成像条件,但是改进的1D 成像条件对一次波成像有很大的适用性,若对含有多次波的记录进行成像,还是不可避免的会带来源于不同反射点的上、下行波场能量而构建出的成像噪音.在以下的篇幅中,用串音干扰成像噪音来表示这种由于多次波的存在而带来的非同源的上、下行波场能量相遇构建的成像值所带来的成像噪音.
为了压制上述由多次波带来的串音干扰成像噪音,更好地适应表层多次波和一次波联合成像,在此引入2D 反褶积成像条件[23].此成像条件在1D 成像条件所表征的时间域约束条件基础上,又增加了震源位置所在的空间域的约束条件,如公式(2)所示:
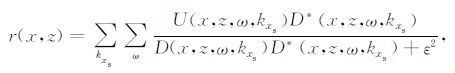
|
(2) |
其中,kxs表示震源波数;U(x,z,ω,kxs)和D(x,z,ω,kxs)表示延拓至地下成像点(x,z),并且在时间域和震源位置所在空间域做2D 傅里叶变换至频率-震源波数域(ω-kxs)的波场.结合上文中表层多次波和一次波联合偏移的基本原理,此处用于延拓的上、下行波分别是包含有表层多次波的原始记录和原始记录与脉冲震源之和;ε2 为保证算法稳定的系数,其表达式如下:
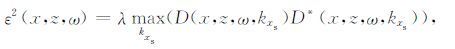
|
其中,λ 为大于0小于1的常数系数,具体值要根据不同的数据具体测试而得.
根据式(2)所示的成像条件,成像点(x,z)处的成像结果是通过延拓至成像点的频率-震源波数域(ω-kxs)的上、下行波场的反褶积基于所有频率和震源波数求和得到,也就是通过提取上、下行波场的反褶积结果中的零延迟分量来得到.则延拓的上、下行波场不仅要在时间上,而且要在空间震源位置上也一致才能满足成像条件.这样,就可以压制由于非同源的上、下行波场能量相关带来的成像噪音,即对含有多次波的记录进行成像时应用常规相关成像条件带来的串音干扰成像噪音.
而且,从上述应用成像条件得出成像结果的过程来分析,常规成像方法是先求出每一炮的偏移结果再把各炮成像结果在对应地下位置上叠加,而基于式(2)所示的2D 成像条件,地下每一个成像点的成像值是将所有对其有贡献的炮集都进行波场延拓以后,再基于时间域和震源位置所在空间域的2D约束成像条件来提取的成像值.
4 模型试算本节结合两个模型数据来检验本文方法的有效性.
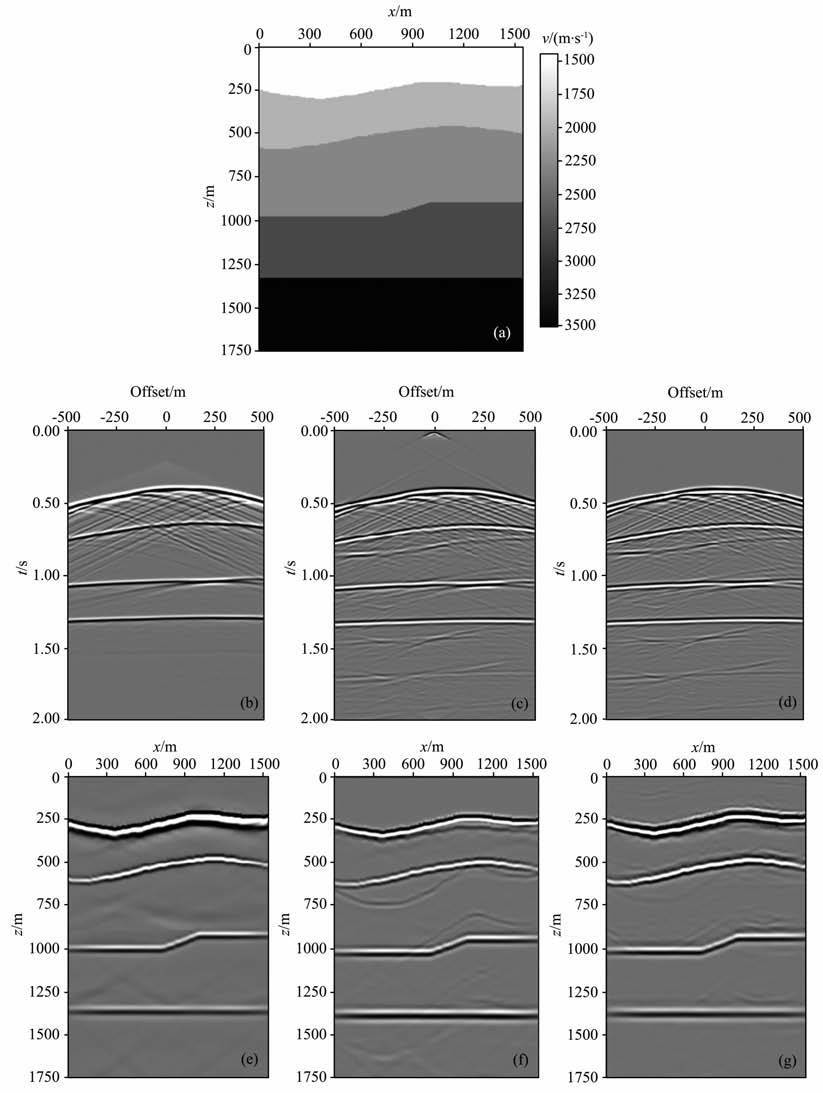
4.1 简单五层模型试算图 3a所示为五层模型速度剖面,其中五层的速度由上至下分别为1500m/s、2000m/s、2300m/s、2800m/s、3500 m/s.根据这个模型正演出两套数据,一套是不含表层多次波的数据,用于常规一次波偏移成像;另一套是包含有表层多次波的数据,用于本文表层多次波和一次波联合成像.图 3b是一次波的一个的单炮响应.图 3c是本文表层多次波和一次波联合成像方法所用的震源波场的一个单炮记录,是原始含有多次波的数据与脉冲震源之和.图 3d是本文成像方法所用的接收波场的一个单炮记录,是将直达波去除以后的包含有表层多次波的接收记录.图 3e是常规一次波偏移成像结果.图 3f是应用常规偏移方法对含有多次波的记录进行成像获得的结果,即用脉冲震源作为震源波场并且用1D 相关成像条件,可以看出,出现了很多由于多次波的存在而带来的成像噪音.图 3g是应用本文的表层多次波和一次波联合成像方法得出的偏移成像结果.通过图 3g和图 3e的成像结果比较,可以得出,本文的多次波成像方法可以实现对地下构造的准确成像;通过图 3g和图 3f的成像结果比较,可以看出,本文的成像方法可以很大程度上压制常规偏移方法对含有多次波的记录进行成像时引入的成像噪音.
|
图 3 简单五层模型成像结果对比 (a)简单五层模型速度剖面;(b)一次波单炮响应;(c)本文表层多次波和一次波联合成像方法所用的震源波场单炮记录;(d)本文成像方法所用接收波场单炮记录;(e)常规一次波偏移结果;(f)应用常规偏移方法对含有多次波的记录进行成像获得的结果;(g)本文表层多次波和一次波联合成像结果. Fig. 3 Five-layer velocity model and migration results (a)The five-layer velocity model used to generate the synthetic data; (b) A representative one shot gather of primaries;c) A representative oneshot gather used for illumination of joint imaging of surface-related multiples and primaries;d) A representative one shot gather used for received shot data of joint imaging of surface-related multiples and primaries; (e) Migration of the primaries;(f) Traditional Migration for shot data including multiples;g)Joint imaging of surface-related multiples and primaries using method presented in the paper. |
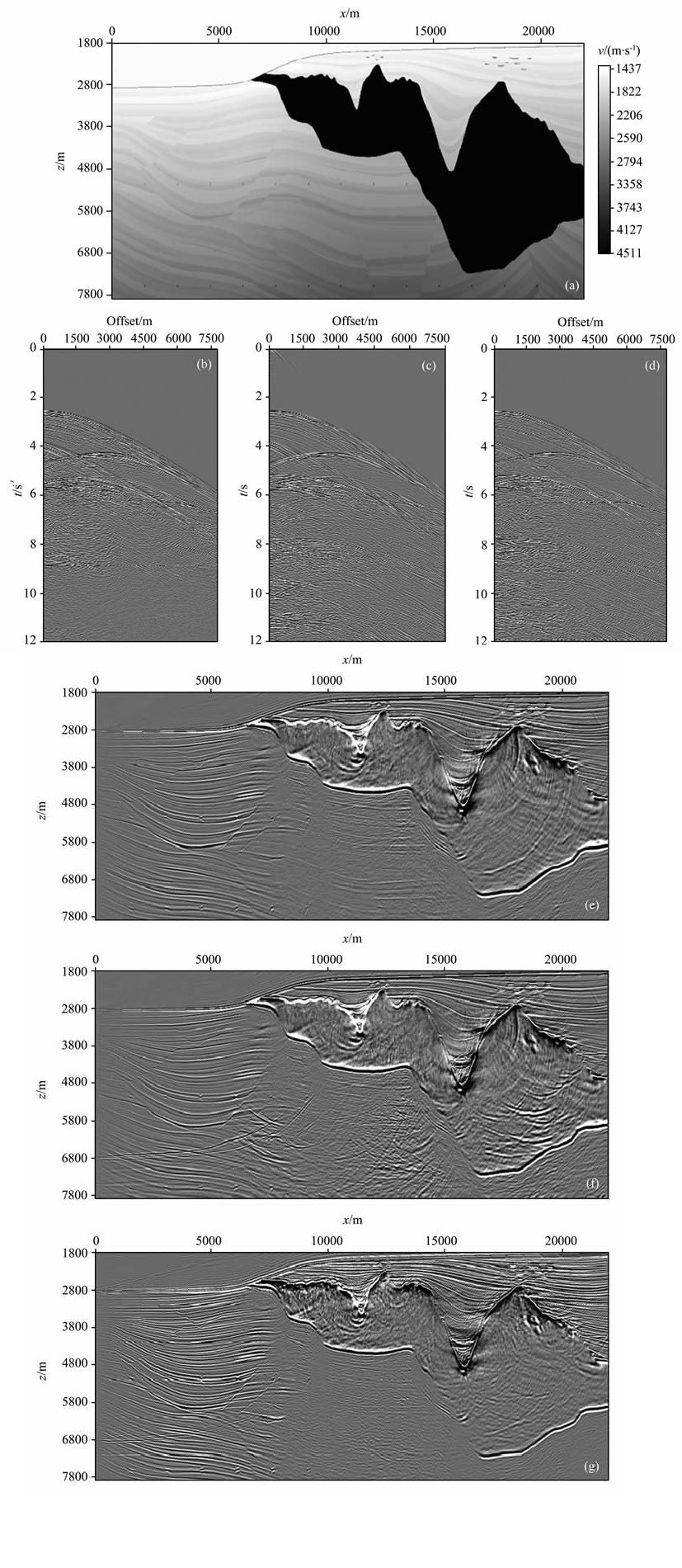
Sigsbee2b模型数据是SMAART(Subsalt Multiples Attenuation And Reduction Team)协会推出的用于多次波数据处理的标准模型数据.合成数据共有496炮,每炮接收道不同,记录长度12s, 时间采样率8 ms.图 4a所示为Sigsbee2b 模型部分速度剖面,此模型中包含一个起伏海底界面,用于产生多次波.模型数据包含有两套数据,一套是不包含表层多次波的数据(NFS),另一套是含有表层多次波的数据(FS).图 4b 是不含有表层多次波的数据(NFS)的一个的单炮响应.图 4c是本文表层多次波和一次波联合成像方法所用的震源波场的一个单炮记录,是含有表层多次波的原始数据(FS)与脉冲震源之和.图 4d是本文成像方法所用的接收波场(FS)的一个单炮记录,是将(FS)记录去除直达波以后的数据.图 4e是一次波数据(NFS)偏移成像结果.图 4f是应用常规偏移方法对含有表层多次波的数据(FS)进行偏移获得的结果,可以看出,此成像结果虽然可以实现对地下构造的正确成像,但存在很多由于多次波的存在而带来的成像噪音.图 4g是应用本文的表层多次波和一次波联合成像方法得出的偏移成像结果.通过图 4g和图 4e的成像结果比较,可以得出,本文的多次波成像方法可以实现对地下构造的准确成像;通过图 4g和图 4f的成像结果比较,可以看出,本文的成像结果中虽然还残留有一些噪音,但是已经很大程度上压制常规偏移方法对含有多次波的记录进行成像时引入的成像噪音.
|
图 4 Sigsbee2b模型成像结果对比 (a)Sigsbee2b模型速度剖面;(b)不含有表层多次波的数据(NFS)的一个的单炮响应;(c)本文表层多次波和一次波联合.成像方法所用的下行震源波场的一个单炮记录;(d)本文成像方法所用的上行接收波场的一个单炮记录;(e)一次波数据(NFS)偏移成像结果;(f)应用常规偏移方法对含有多次波的记录进行成像获得的结果;(g)本文的表层多次波和一次波联合成像方法得出的偏移成像结果. Fig. 4 Stratigraphic interval velocity model for Sigsbee2b dataset and migration results (a) Stratigraphic interval velocity model for Sigsbee2b dataset; (b) A representative one shot gather of primaries without surface-relatedmultiples (c) A representative one shot gather used for ilummation of joint imaging of surface-related multiples and primaries ;d) Arepresentative one shot gather used for received shot data of joint imaging of surface-related multiples and primaries; (e) Migration of theprimaries; (f) Traditional Migration for shot data ncluding multiples; (g) Joint imaging of surface-related multiples and primaries usingmethod presented n the paper |
和常规对多次波进行压制的处理思路不同,本文利用多次波的信息为地震成像服务;和单独对多次波进行成像的方法也不同,本文同时利用表层多次波和一次波进行联合成像,不需要预先进行多次波的识别以及多次波和一次波的分离.根据表层多次波的特点,本文基于广义概念上的炮偏移成像算法,对常规一次波偏移方法从用于向下延拓的上、下行场以及成像条件方面进行了改进,将同时含有表层多次波和一次波的记录用于上行波场的逆向延拓,将含有表层多次波的记录与脉冲震源之和用于下行正向波场的延拓,并应用2D 反褶积成像条件进行成像,实现了表层多次波和一次波联合成像.在数值试验部分,通过将本文所述方法的成像结果和常规一次波偏移结果以及常规偏移方法对含有多次波的记录进行成像获得的结果相比较,表明本文表层多次波和一次波联合成像方法可以压制常规成像方法中由多次波带来的成像噪音,实现同时利用表层多次波和一次波来进行地下构造的准确成像.根据方法的实现过程可以得出,本文所述方法比较适用于海上拖缆观测数据和陆上观测系统含多次波数据.
| [1] | Yilmaz O. Seismic data processing. Society of Exploration Geophysics,1987 |
| [2] | Foster D J, Mosher C C. Suppression of multiple reflections using the Radon transform. Geophysics , 1992, 57(3): 386-395. DOI:10.1190/1.1443253 |
| [3] | Lokshtanov D. Multiple suppression by data-consistent deconvolution. The Leading Eage , 1999, 18(1): 115-119. DOI:10.1190/1.1438136 |
| [4] | Lamont M G, et al. Multiple attenuation using the MMO and ISR preconditioning transforms. The Leading Eage , 1999, 18(1): 110-114. DOI:10.1190/1.1438134 |
| [5] | Berkhout A J, Verschuur D J. Estimation of multiple scattering by iterative inversion, Part I : Theoretical considerations. Geophysics , 1997, 62(5): 1586-1595. DOI:10.1190/1.1444261 |
| [6] | Verschuur D J, Berkhout A J, Wapenaar C P A. Adaptive surface-related multiple elimination. Geophysics , 1992, 57(9): 1166-1177. DOI:10.1190/1.1443330 |
| [7] | Guitton A. Multiple attenuation with multidimensional prediction-error filter. 73th Ann. Internat. Mtg., Soc. Expl. Geophys., Expanded Abstracts,2003. 57-74 |
| [8] | Spitz S. Pattern recognition, spatial predictability, and subtraction of multiple events. The Leading Edge,1999,55-58 http://www.oalib.com/references/18985600 |
| [9] | 李鹏, 刘伊克, 常旭, 等. 多次波问题的研究进展. 地球物理学进展 , 2006, 21(3): 888–897. Li P, Liu Y K, Chang X, et al. Progress on the multiple problems. Progress in Geophysics (in Chinese) , 2006, 21(3): 888-897. |
| [10] | Reiter E C, Toksoz, M N, Keho T H, et al. Imaging with deep-water multiples. Geophysics , 1991, 56(7): 1081-1086. DOI:10.1190/1.1443119 |
| [11] | Sheng J. Migration multiples and primaries in CDP data by crosscorrelogram migration. 71th Ann. Internat. Mtg., Soc. Expl. Geophys., Expanded Abstracts,2001. 1297-1300 |
| [12] | Yu J, Schuster G. Crosscorrelogram migration of IVSPWD data. 71th Ann. Internat. Mtg., Soc. Expl. Geophys., Expanded Abstracts, 2001. 456-459 |
| [13] | Berkhout A J, Verschuur D J. Multiple technology:Part 2, migration of multiple reflections. 64th Ann. Internat. Mtg., Soc. Expl. Geophys., Expanded Abstracts, 1994.1497-1500 |
| [14] | Guitton A. Shot-profile migration of multiple reflections. 72th Ann. Internat. Mtg., Soc. Expl. Geophys., Expanded Abstracts, 2002.1296-1299 |
| [15] | Shan G. Source-receiver migration of multiple reflections. 73th Ann. Internat. Mtg., Soc. Expl. Geophys., Expanded Abstracts, 2003. 1008-1011 |
| [16] | Berkhout A, Verschuur D. Transformation of multiples into primary reflections. 73th Ann. Internat. Mtg., Soc. Expl. Geophys., Expanded Abstracts, 2003. 1925-1928 |
| [17] | Youn O, Zhou H W. Depth imaging with multiples. Geophysics , 2001, 66(1): 246-255. DOI:10.1190/1.1444901 |
| [18] | Brown M. Least-squares joint imaging of primaries and multiples. 72th Ann. Internat. Mtg., Soc. Expl. Geophys., Expanded Abstracts, 2002. 1497-1500 |
| [19] | Brown M P, A Guitton. Least-squares joint imaging of multiples and primaries. Geophysics , 2005, 70(5): 79-89. DOI:10.1190/1.2052471 |
| [20] | Muijs R, Robertsson J O A, Holliger K. Prestack depth migration of primary and surface-related multiple reflections:Part I — Imaging. Geophysics , 2007, 72(2): S59-S69. DOI:10.1190/1.2422796 |
| [21] | 李振春. 地震成像原理与方法. 东营: 石油大学出版社, 2004 . Li Z C. theory and method of seismic imaging (in Chinese). Dongying: China University of Petroleum Press, 2004 . |
| [22] | 叶月明, 李振春, 仝兆岐, 等. 双复杂条件下带误差补偿的频率空间域有限差分法叠前深度偏移. 地球物理学进展 , 2008, 23(1): 136–145. Ye Y M, Li Z C, Tong Z Q, et al. Xwfd pre-stack depth migration based on dual-complexity with error compensation correction. Progress in Geophysics (in Chinese) , 2008, 23(1): 136-145. |
| [23] | Valenciano A, Biondi B. 2D deconvolution imaging condition for shot profile migration.73 th Ann. Internat. Mtg., Soc. Expl. Geophys., Expanded Abstracts, 2003. 1059-1062 |
 2011, Vol. 54
2011, Vol. 54

