2. 成都理工大学地球物理学院地球物理与勘察技术系, 成都 610059;
3. Rock Physics Lab of Geoscience Department, University of Houston, Houston 77036 USA;
4. 中国石油大学CNPC物探重点实验室, 北京 102249
2. Department of Geophysics and Exploration, College of Geophysics, Chengdu University of Technology, Chengdu 610059, China;
3. Rock Physics Lab of Geoscience Department, University of Houston, Houston 77036, USA;
4. 4. CNPC Key Laboratory of Geophysical Prospecting, China University of Petroleum, Beijing 102249, China
未固结碎屑砂岩储层是重要的油气储层类型之一,近几年在渤海、珠江口相继发现和投入开发了一批疏松砂岩油气藏,这在客观上要求对未固结碎屑砂岩地震弹性特征进行深入研究以便为该类油气储层地震资料解释及岩性预测提供依据.未固结碎屑砂岩的地震弹性性质可用颗粒集合体的弹性性质来类比,为解释接触颗粒在压力下的弹性性质,最早使用Hertz接触模型求出接触颗粒边界的法向压缩刚度,Mindlin对Hertz接触模型进行了推广给出在剪应力作用下接触颗粒边界的剪切刚度[1].在此基础上Walton等[2, 3]给出了随机堆积的球形颗粒集合体的等效模量表达式,即基于Hertz-Mindlin 接触模型的等效介质模型或称Hertz-Mindlin等效介质模型.该模型的理论计算结果表明介质的等效体积模量(K)、剪切模量(G)与围限压力(P)满足关系:K-G∝P1/3,而泊松比仅为介质组成颗粒弹性性质的函数.Zimmer等从实验和理论两个方面对颗粒介质的地震弹性性质进行了研究,实验结果表明模量与压力的指数关系并不固定,而是在1/3-1/2间变化,同时等效介质模型所给出的剪切模量理论计算结果与实验结果之间存在较大的偏差[4-6].Bachrach等[7]考虑实际岩石介质中组成颗粒的不规则突起,在Hertz-Mindlin 等效介质模型中用颗粒接触面局部平均曲率半径代替颗粒平均半径以解释理论计算结果与实验测量结果的差异.
颗粒介质是由众多离散颗粒组成的软凝聚态物质,其地震弹性特征相对于连续介质表现的更为复杂,对颗粒介质的等效弹性性质的研究是一个涉及微观尺度的单颗粒、细观尺度的力链和宏观尺度的颗粒体系的多尺度力学问题,其核心是细观尺度的力链结构及演化,因此研究颗粒介质的宏观等效弹性性质也需要从微观颗粒和细观力链尺度入手.离散元法是研究颗粒介质细观尺度力链结构的形成及演变规律的有效工具,其思想起源于分子动力学,在研究颗粒介质等非连续体力学响应问题中已经得到广泛运用[5, 8-11].本文利用颗粒介质的3D 离散元方法从微观颗粒尺度和细观力链尺度分析Hertz-Mindlin等效介质模型产生预测误差的可能物理机制,在此基础上利用自定义切向刚度校正因子C及组合参数R/R定量反映颗粒松弛作用及颗粒不规则性的影响,给出等效介质模型的理论校正公式,并对实际资料进行处理验证了方法的正确性和有效性.
2 Hertz-Mindlin等效介质模型 2.1 颗粒接触力学模型未固结碎屑砂岩具有典型的粒状结构特征,由石英、长石等组成颗粒通过一定的接触方式构成岩石骨架,其物理本质是由众多离散颗粒组成的软凝聚态物质,相邻颗粒间通过发生接触形变使得能量在颗粒间进行传播,因此微观颗粒接触力学特征及其在应力、应变扰动下的颗粒动力学特征是研究集合体等效弹性特征的关键之一.
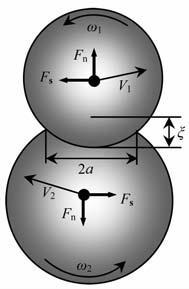
在一定的压力作用下,半径分别为R1和R2 的球形颗粒1与球形颗粒2发生接触,如两颗粒球心位置矢量分别为r1 和r2,则所形成法向重叠量ξ 可表示为(图 1)
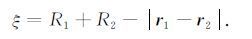
|
(1) |
|
图 1 颗粒接触模型 Fig. 1 Contact model of contacting particles |
由颗粒之间相互接触而产生的接触力包括垂直于接触面的法向接触力Fn 和由摩擦产生的平行于接触面方向的切向接触力Ft (图 1).其中Fn 可表示为[12, 13]
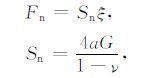
|
(2) |
式中Sn 为颗粒接触面的法向等效刚度,G、ν 分别为组成颗粒的剪切模量与泊松比.a为颗粒接触面半径,在一定静水压力P作用下可表示为[12, 13]

|
(3) |
式中R 为接触颗粒面的局部平均曲率半径,对于理想球形颗粒其值等于(R1R2)/(R1+ R2);n为单个颗粒接触面的个数(颗粒配位数),Φ 为介质孔隙度.
切向接触力Ft 表现的较为复杂,其大小依赖于加载历史,并不完全能由颗粒的相对位置决定.如用法向接触力增量ΔFn 与切向接触力增量ΔFt 来描述颗粒的加载历史,切向接触力Ft 可由下式计算[3, 12, 13]:

|
(4) |

|
(5) |
式中St 为切向等效刚度,Δζ 为切向位移增量,μf、Fmaxs分别为库仑摩擦系数和静摩擦力.从(4)式可以看出,当接触力增量在颗粒接触面不形成微观滑动时(${\left. {\Delta {F_t}} \right. < F_{\max }^s = {\mu _f}\Delta {F_n}}$),切向力增量ΔFt 与切向位移增量Δζ 不仅依赖于加载历史,也受到法向接触力的影响,该式亦称为Mindlin接触模型[1].在一定的边界条件下,切向力增量ΔFt 并不形成切向位移增量Δζ 来达到局部颗粒尺度的平衡状态,而是产生作用于颗粒中心的力矩Mi =-di ΔFt , 其中di 是颗粒i的中心到接触点的距离.在力矩的作用下,相互接触的颗粒发生旋转、重排列等局部运动而并不形成切向位移增量Δζ,这种颗粒运动结果同样可使作用在颗粒上的合力为零而局部达到平衡状态,也使作用在介质上的应力扰动发生应力松弛现象.
2.2 等效介质模型等效介质模型建立了颗粒介质宏观弹性性质与颗粒微观力学特征参数的联系,其理论基础是颗粒系统在宏观应力作用下的应变能等于作用于系统所有组成颗粒接触点处的应变能总和,介质等效弹性模量则可通过对应变能密度求导得到[3, 14].假定组成介质的单个颗粒具有相同的接触点(面)个数n,且颗粒变形满足均匀应变假设,即处于xi 位置的颗粒在时间间隔δt内的位移(δui )与介质宏观应变率(${\dot \varepsilon _{ij}}$)满足关系δui =${\dot \varepsilon _{ij}}$xjδt,则应变能密度U表示为
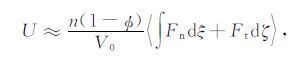
|
(6) |
式中F0 为单个颗粒的体积.考虑到切向力Ft 的大小依赖于加载历史,利用公式(6)计算颗粒介质的等效弹性模量需要分成两种情况,其一是库仑摩擦系数μf=0,即Ft =0(见公式(5)),此时颗粒集合体的等效体积模量Keff与等效剪切模量Geff分别表示为[3, 12, 13]
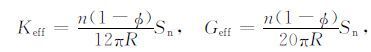
|
(7) |
式中R代表颗粒的等效半径;另一种情况是库仑摩擦系数μf- ∞,即颗粒接触边界满足“焊接"接触,此时颗粒集合体的等效体积模量不变,而等效剪切模量Geff表示为[3, 12, 13]
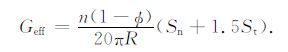
|
(8) |
上述等效介质模型成立的条件是要求颗粒变形满足均匀应变假设,而颗粒之间的接触力尤其是切向接触力在一定的条件下会形成相对于颗粒接触点的力矩使颗粒发生旋转、重排列等松弛作用,颗粒的变形不再满足均匀应变假设.式(8)同时要求颗粒接触满足“焊接"接触条件,而颗粒实际接触条件并不总满足该条件.因此在使用等效介质模型时必须要考虑上述两种作用对计算结果的影响.
3 颗粒介质力学响应的离散元(DEM)模拟 3.1 离散元模拟的基本原理离散元法是把颗粒介质看作有限个离散单元的组合,每个组成颗粒作为一个离散单元,根据过程中的每一时间步各颗粒间的作用和牛顿运动定律的交替迭代预测散体群的行为.本次数值模拟中采用球形颗粒代替未固结碎屑砂岩的主要组成颗粒石英,颗粒在如图 1中的力学体系下其运动形式可由线性运动和转动构成,并在每个时间步长Δt内满足Newton方程[10, 15]:
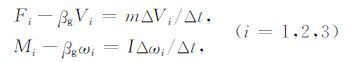
|
(9) |
式中Fi 、Mi 分别为作用在给定颗粒上的合力与合力矩,Vi 、ΔVi 分别为线速度及其增量,ωi 、Δωi 分别为角速度及其增量,m、I分别为颗粒质量及转动惯量,βg 为系统整体阻尼.通过积分解公式(9)得到平均线速度及角速度,进而计算颗粒的线位移与角位移(θ)并得到颗粒的新位置:

|
(10) |
由各球的新位置坐标可决定相邻颗粒是否接触或原接触点是否脱离.相互接触的球会产生假性重叠量,即弹塑性变形ξ(图 1),由接触模型公式(2)-(5)分别求出接触力Fi 、Mi ,再返回(9)式迭代.
当两颗粒发生接触变形时,接触面受到交变应力作用而产生沿颗粒表面传播的瑞利偏振波,总能耗的70%是通过这种瑞利波消耗的.两颗粒间的接触作用应仅限于发生碰撞的两颗粒上,而不应该通过瑞利波传递到其他颗粒上,因此DEM 方法中的时间步长的选择应小于瑞利波传递半球面所需要的时间,对于由i组不同颗粒所构成的颗粒系统其时间步长可表示为[5, 13, 16]
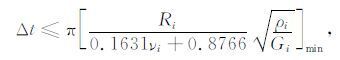
|
(11) |
式中ρi 、Gi 分别为组成颗粒的密度与剪切模量.本文主要研究未固结碎屑砂岩的弹性特征,石英颗粒是实际岩石的基本构成颗粒,选择石英剪切模量为G=44GPa、颗粒半径R=0.5mm、泊松比ν=0.06,这样Δt≤10-7s.
在离散元法中可通过颗粒介质的应力、应变响应关系来确定系统的宏观弹性特征.在一定围限压力条件下按不同堆积方式生成颗粒系统,对颗粒系统施加一个很小的应变扰动Δε 作为模拟的初始条件,利用离散元法确定系统的应力、应变响应随时间的变化,在系统达到平衡后通过应力增量Δσ 与应变扰动Δε的比值来确定系统的弹性模量.本文通过纯剪实验研究颗粒介质的剪应力及剪切模量特征(Δεzz =Δεxx ≠0),在该力学过程中剪应力增量(Δτ)与剪切模量GDEM 可表示为
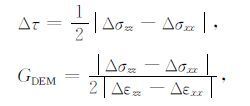
|
(12) |
体积模量KDEM通过z方向的单轴压缩实验(Δεzz ≠0)求取,在该力学过程中体积模量KDEM 可表示为
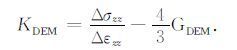
|
(13) |
颗粒介质离散元模拟选用长方体试样,试样高度为40mm, 底面为宽度为20 mm 的正方形,球形颗粒的粒径在0.4-0.6mm 之间均匀分布,初始孔隙度为0.35,长方体试样所含颗粒总数为17200(图 2a).试样所含颗粒的初始状态为紧密、随机、各向同性排列,颗粒密度取为2.65×103kg/m3,颗粒之间的摩擦系数为1,颗粒接触力学特征满足Hertz-Mindlin接触模型(式(2)、(4)),时间步长取1×10-7s.对该试样分别在一定的围限压力下进行单轴与纯剪加载试验,即在给定围限压力下系统颗粒达到平衡后再通过施加不同轴向的应变扰动来实现单轴压缩与纯剪数值模拟.
|
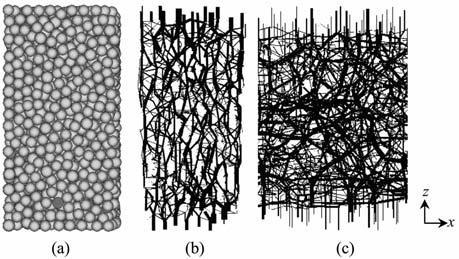
图 2 随机排列颗粒介质模型及二维接触力链结构 (a)颗粒模型;(b)单轴压缩力链结构;(c)纯剪切力链结构. Fig. 2 Random arrangement of granular assembly and 2D contact force chain structure (a)Model of granular packing; (b) Force chain under uniaxial compression; (c) Force chain under pure shear. |
图 2b为单轴压缩模拟中系统应变ε=0.5%时的颗粒细观力链二维分布形式(平行y轴切片),图中的浅灰色线表示弱力链,深灰黑色线则表示强力链,线的粗细正比于接触力的大小.在单轴压缩模拟中强力链呈准直线形,与压缩方向(应力方向)一致并贯穿整个颗粒系统,从长方体试样底部向中部力链强度逐渐减弱;在这种细观接触力作用下颗粒表现出与系统宏观应力、应变方向一致的细观位移,颗粒的细观位移大小并不一致表现出一定的不均匀性,表现为位移从底部向中部也呈逐渐减小的趋势(图 3a).图 2c为纯剪模拟中系统应变ε=0.5% 时的颗粒细观力链分布形式,接触力较大的强力链沿着近似平行于主应力面的方向排列,这些力链将颗粒体分隔成稀疏的菱形网络结构;在颗粒二维细观位移矢量图中,颗粒的位移表现出特定的涡状结构特征,反映出颗粒在细观尺度上所存在的相对滑动、转动、颗粒重排列等非线性运动(图 3b).

|
图 3 颗粒介质二维位移结构(箭头方向代表位移方向) (a)单轴压缩位移结构;(b)纯剪切力位移结构. Fig. 3 2D displacement structure of granular assembly (arrows present the direction of displacement) (a)Displacement structure of uniaxial compression;(b) Displacement structure of pure shear. |
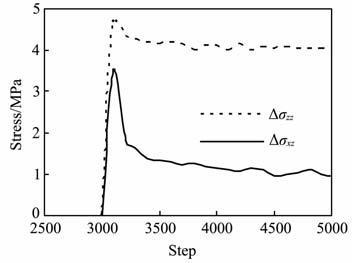
图 4中给出颗粒介质模型在单轴压缩模拟中轴向应力增量(Δσzz )与纯剪模拟中剪应力增量(Δτ)随系统平衡时间(运行次数)的变化.数值模拟过程中系统所给定的围压为0.5MPa, 在3000个时间步长内系统达到初始平衡状态(系统动能小于给定值).从第3000步开始在10个时间步长内使系统的宏观应变ε=0.1%,并保持宏观应变使系统逐渐松弛达到平衡状态.在两类实验中应力增量的变化均可分为加载硬化阶段、松弛软化阶段与松弛平衡阶段三个过程,快速加载硬化阶段代表颗粒介质的瞬时弹性响应,此时介质所表现出的力学行为更接近于弹性介质,随后的松弛过程中切应力增量(Δτ)相对于其硬化峰值明显降低表现出明显的黏弹性介质行为,造成这种现象的主要原因是在该阶段颗粒通过旋转、滑动以及颗粒重排列等非线性运动使系统发生明显的剪应力松弛(图 3b).用硬化峰值与松弛平衡后的Δτ 所计算出的剪切模量(公式(12))是有明显差异,而利用硬化峰值所计算的结果应与公式(8)一致,两者均反映相同的物理本质,即颗粒在微观尺度上无旋转、重排列等松弛作用的结果,颗粒接触边界表现为“焊接"接触,因此在使用等效介质模型计算颗粒介质剪切模量时需要考虑松弛作用的影响.轴向应力增量(Δσzz )在松弛过程中则相对变化较小,其主要原因是颗粒在细观尺度上应力和应变的图 4 Δσzz 与Δτ 随系统平衡时间(运行次数)的变化Fig.4 ThechangeofΔσzz andΔτwithequilibrationtime(runningsteps)ofgranularsystemchainstructure方向基本是一致的(图 2b),虽然应变是不均匀的但并没有形成明显的由颗粒旋转、重排列等形成的应力松弛作用,不均匀应变结果与均匀应变近似,用硬化峰值与松弛平衡后的Δσzz 所计算出的体积模量并无明显差异,而用硬化峰值所给的结果应与体积模量等效介质模型(公式(7))一致,因此在利用等效介质模型计算颗粒介质体积模量时可以不进行松弛作用校正.
|
图 4 Δσzz 与Δτ 随系统平衡时间(运行次数)的变化 Fig. 4 The change of Δσzz and Δτ with equilibration time(running steps) of granular system chain structure |
通常利用球形粒状集合体的弹性特征来定量类比未固结碎屑砂岩在一定储层条件下的地震弹性性质.地震勘探中假定在一定上覆压力作用下组成介质的颗粒接触条件满足Hertz-Mindlin 接触模型,即颗粒接触面表现为“焊接"接触,颗粒之间不存在相对滑动、旋转、重排列等松弛作用,从而利用公式(8)来计算具有随机堆积特征的颗粒介质的等效剪切模量.从第3节讨论结果可知颗粒松弛作用对介质等效剪切模量的计算有明显的影响,是使等效介质模型出现偏差的主要原因,因此在使用等效介质模型计算未固结碎屑砂岩地震弹性属性(尤其是与剪切模量相关的地震弹性属性)时需要进行一定的区域校正以考虑松弛作用的影响.
4.1 等效介质模型的校正疏松碎屑砂岩在沉积与压实过程中颗粒接触面通常不完全满足“焊接"接触条件,假定颗粒接触面的平均摩擦系数为μ,则切向刚度St 可表示为
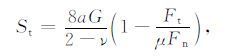
|
(14) |
式中Fn 与Ft 分别为颗粒接触边界所作用的正压力和剪切力.当剪切力Ft =μFn 时,St=0(最小值);在摩擦系数μ 趋于无穷时(“焊接"接触条件),切向刚度St 的计算结果与公式(4)一致,达到最大值.可对公式(14)做等效处理,即假定半径为a的颗粒接触面中只有部分满足“焊接"接触条件,用系数C1 表示颗粒接触面中满足“焊接"接触条件的等效部分,公式(14)可简化为
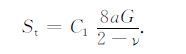
|
(15) |
系数C1 对于疏松碎屑砂岩是一个反映颗粒接触面平均物理特征的统计量,并与介质的沉积与压实历史密切相关,其值在0-1的范围内变化.
对于粒状介质,定量表征颗粒旋转和重排列运动对介质等效弹性特征的影响是比较困难的,考虑到这种松弛作用主要表现为对介质等效剪切模量的影响,其作用等效于减小颗粒接触面中满足“焊接"接触条件的等效部分,可定义系数C2 表示松弛作用的等效影响,则公式(14)可表示为
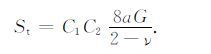
|
(16) |
系数C2 的值也可在0-1的范围内变化,系数C1 和C2 是反映两种不同物理机制的影响,但在一定程度上系数C2 是依赖于C1 的,颗粒接触面的条件越接近“焊接"接触(C1 的值越大),松弛作用的影响也会越弱(C2 的值也会越大).定义系数C=C1C2,公式(16)可简化为
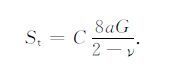
|
(17) |
综合公式(3)、(7)、(8)、(17)可得到校正公式:
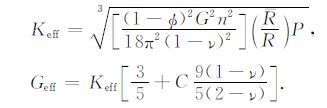
|
(18) |
利用等效介质模型的校正公式计算疏松砂岩弹性模量需要确定两组参数(见公式(18)):其一反映颗粒形状或颗粒接触面局部特征的组合参数R/R,其中R 为接触颗粒面的局部平均曲率半径,在一定程度上反映接触颗粒的磨圆度,R代表颗粒的等效半径;另一个参数是表征颗粒接触面特征与松弛作用影响的切向刚度校正因子C.从公式(18)中可以进一步推导出干燥条件下疏松粒状集合体泊松比(σdry)的计算公式:
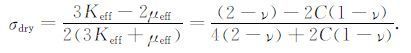
|
(19) |
从公式(19)可以看出,干燥条件下介质的泊松比(σdry)仅依赖于切向刚度校正因子,而与组合参数R/R无关,因此可利用泊松比先求出切向刚度校正因子C,再利用公式(18)中的体积模量校正公式得到组合参数R/R的拟合值,得到两组参数后再利用公式(18)与Gassmann公式计算特定储层条件下未固结砂岩的弹性模量.
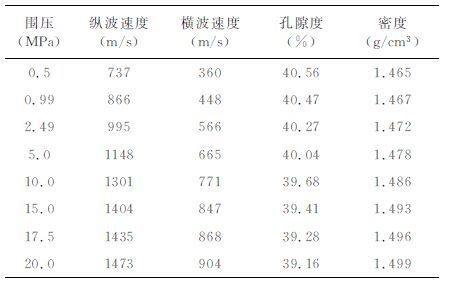
从前面的分析可以知道,在不考虑组成颗粒不规则形状的条件下Hertz-Mindlin等效介质模型可给出较为准确的体积模量理论计算值.图 5 中给出一组由光滑球形玻璃珠所构成的人工疏松颗粒集合体在不同围限压力下利用超声波速度测量结果所计算出的等效体积与剪切模量值(见表 1及文献[4]),利用公式(18)可以计算出组合参数R/R取不同值时的体积模量随压力变化的理论曲线,计算时取组成颗粒剪切模量G=29GPa, 泊松比ν=0.19,孔隙度Φ 与颗粒配位数n的取值均进行了对应压力校正(见文献[4]).在组合参数R/R取值为1 的情况下Hertz-Mindlin等效介质模型所给出的压力-体积模量理论变化曲线与实际颗粒集合体的体积模量结果相符合(图 5a),表明公式(18)中的组合参数R/R在一定程度上可以用来反映颗粒形状或颗粒接触面局部特征.图 5b 为组合参数R/R为1 时,切向刚度校正因子C变化时的剪切模量随压力变化的理论曲线,当C=1时代表Hertz-Mindlin等效介质模型理论计算结果,此时颗粒接触边界的力学特征满足“焊接"接触条件,应力松弛等非线性作用不能发生,介质的等效剪切模量具有最大值;C=0代表颗粒接触面光滑无静摩擦情况,介质的等效剪切模量具有最小值.可以看出,Hertz-Mindlin等效介质模型理论计算结果明显高于实验测量结果,表明颗粒集合体在该实验条件下并不满足“焊接"接触条件,在压力小于5 MPa时颗粒接触边界力学条件更接近于完全光滑接触(C=0),随压力增加颗粒接触面满足“焊接"接触条件的等效部分也逐渐增加,表现为实验测量结果所具有的C值不断增大.
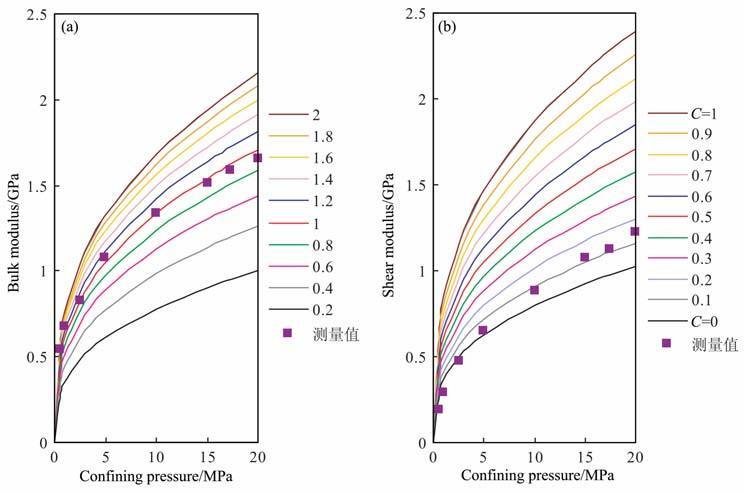
|
图 5 玻璃珠颗粒集合体弹性模量测量值与理论模型计算结果比较 (a)组合参数R/R变化;(b)切向刚度校正因子变化. Fig. 5 Comparison the model predictions to measured data modulus of glass bead packing (a)Change of the combined parameters oi R /R; (b)Change of the calibration factor of shear stiffness. |
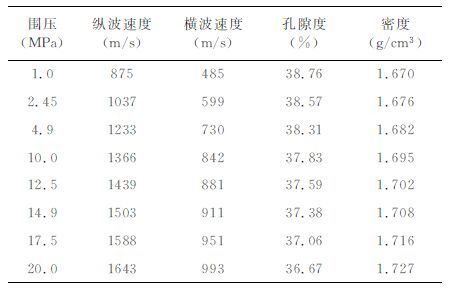
图 6中给出Pomponio未固结人工砂岩样品在干燥条件下的体积与剪切模量测量结果(见表 2 及文献[4]),组成石英颗粒为形状不规则的纯净Pomponio海岸砂,同样可利用公式(18)计算出组合参数R/R取不同值时的体积模量随压力变化的理论曲线(图 5a).图中可见,利用未进行形状校正的Hertz-Mindlin等效介质模型所给出的体积模量理论值(相当于公式(18)中R/R=1)与实验测量结果之间存在明显差异,实验结果与R/R=1.4的理论计算结果更为符合,一定程度上说明组成颗粒具有非球形的不规则形状.图 6b 为组合参数R/R为1.4时,切向刚度校正因子C变化时的剪切模量随压力变化的理论曲线,当C=1 时,Hertz-Mindlin等效介质模型理论计算结果同样明显高于实验测量结果,表明颗粒集合体在该实验条件下也不完全满足“焊接"接触条件,在压力为2.5MPa时颗粒接触边界力学条件更接近于完全光滑接触(C=0),C值随压力增加而不断增大,同样说明在压力作用下颗粒接触面中满足“焊接"接触条件的等效部分会相应增加,介质的等效剪切模量也会随之增大.形成上述现象的主要原因是随围限压力的增加集合体组成颗粒间的“互锁"现象增强造成接触颗粒的接触面摩擦阻力增加,颗粒接触面逐渐偏离完全光滑接触,在相同的应变扰动下颗粒相对滑动等非线性运动减弱.
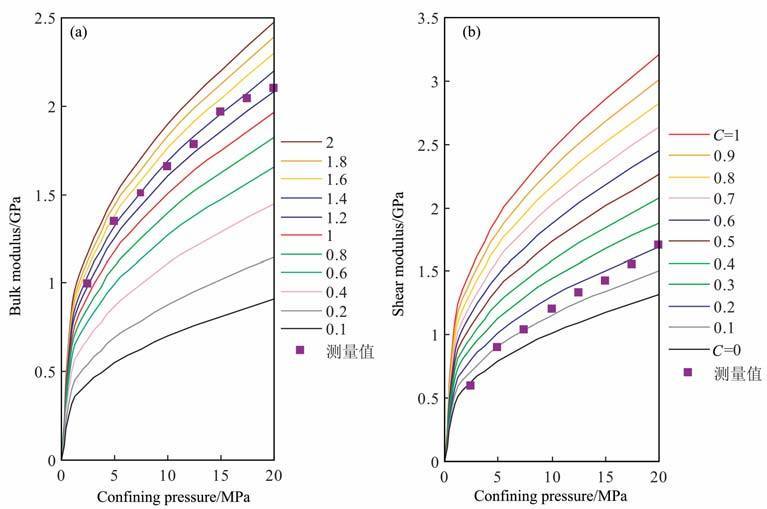
|
图 6 未固结砂岩样品测量与理论模型计算结果比较 (a)组合参数R/R变化;(b)切向刚度校正因子变化. Fig. 6 Comparison the model predictions to measured data of unconsolidated sands (a) Change of the combined parameters of R/R; (b) Change of the calibration factor of shear stiffness. |
|
|
表 2 Pomponio 人工砂岩样品测量结果(引自文献[4]) Table 2 Measurement results of Pomponio sand packing (from Ref.[4]) |
图 7给出墨西哥湾某井中浊积碎屑岩储层的测井响应特征.根据自然伽马曲线可以划分出2 个主要的砂岩层段,分别标记为S1与S2.砂岩层均为高孔隙度的未固结碎屑砂岩,孔隙度在每个层段内变化不大,同时自然伽马曲线也较稳定(除在5075ft存在小的泥岩段),反映出每个砂岩层段的粘土含量差异不大.对于未固结碎屑砂岩,在不含胶结物的情况下其孔隙度的变化主要受分选性与粘土含量的控制.由于理论计算所使用的Hertz-Mindlin 等效介质模型(公式(8))及其校正模型(公式(18))仅适用于等径球形颗粒集合体,同时测井曲线反映出两个层段中砂岩孔隙度及粘土含量差异不大,为简化模型计算近似可认为每个层段中的砂岩是在相同水动力环境下沉积的,具有相同的组成颗粒特征,即组合参数与切向刚度校正因子C在每个砂岩层段是近似相同的.应该注意到相似的孔隙度和泥质含量并不一定意味着砂岩有相同的颗粒大小,从密度及孔隙度测井结果可以看出S1与S2砂层段组成颗粒在分选性上存在一定的差异,分选性差异对未固结疏松砂岩的纵、横波速度均有一定的影响,表现为随疏松砂岩分选性变差其纵、横波速度逐渐增加,用临界孔隙度校正的Hashin-Shtrikman 弹性下限模型可给出高孔隙度条件下未固结砂岩准确的速度(弹性模量)-孔隙度变化关系以反映分选性的影响[4, 13, 17].但分选性变化仅能使未固结砂岩的纵、横波速度随孔隙度表现很平缓的变化,通常不是未固结砂岩横波速度明显偏离Hertz-Mindlin等效介质模型理论结果的主要因素.
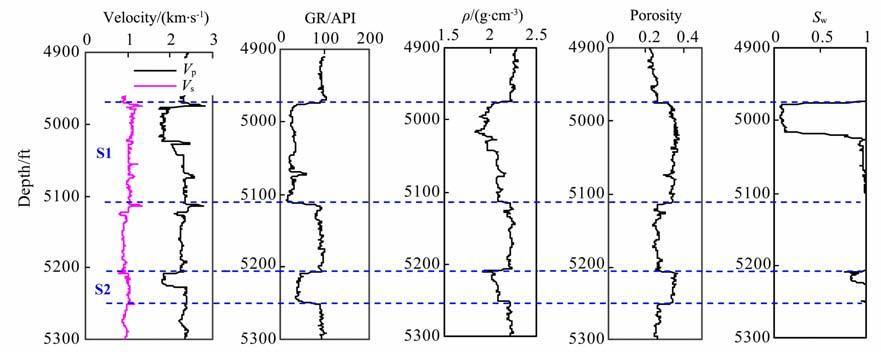
|
图 7 未固结碎屑砂岩储层测井响应特征 Fig. 7 The well-logging data of unconsolidated sands reservoir |
利用公式(7)、(8)可得出等效介质模型在未做校正时所给出的体积与剪切模量理论计算结果,相当于对应储层条件下理想等大球形集合体在“焊接"接触条件下的理论值,此时组合参数R/R与切向刚度校正因子C均等于1,同时利用纵波速度、横波速度及密度测井数据可得到对应储层条件下的体积与剪切模量实际测量结果,对于每个砂岩层段剪切模量的理论计算值均远高于测井结果,而体积模量理论值与测井结果之间仅表现出较小的差异(图 8d、8e).利用纵、横波测井数据得到对应干燥条件下的泊松比曲线(图 8a),依据公式(19)计算出对应砂层的切向刚度校正因子(C)曲线(图 8b),对于S1砂层该值约为0.23,而对于S2 砂层该值约为0.30,可能反映了压实作用对切向刚度校正因子的影响,即压实作用增强会增大因子C的值使得颗粒接触面更接近于“焊接"接触.在得到校正因子(C)曲线的基础上,可利用公式(19)中体积模量的校正公式计算出组合参数R/R的变化曲线(图 8c),对于S1、S2两砂岩储层该值均约为1,反映出组成砂岩颗粒的粒径较为均匀且磨圆度也较好.再将得到的校正因子(C)曲线与组合参数R/R曲线代入等效介质模型的校正公式中计算出疏松砂岩在对应储层条件下的体积与剪切模量值,此时校正的等效介质模型给出了准确的体积与剪切模量预测值(图 8d、8e).
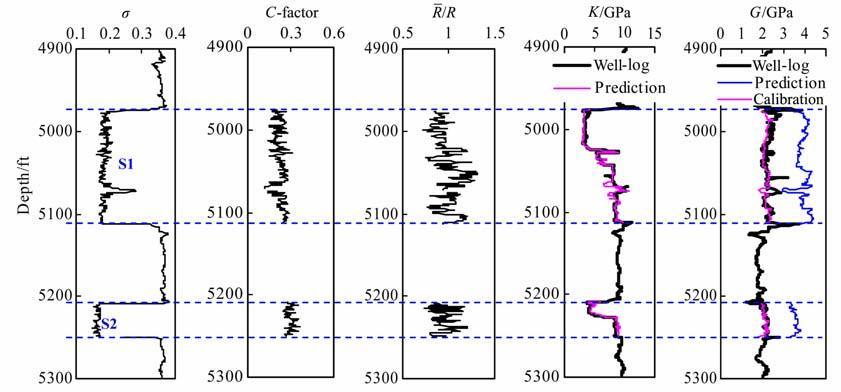
|
图 8 测井计算结果与模型计算结果比较 (a)泊松比;(b)切向刚度校正因子;(c)组合参数R/R;(d)体积模量;(e)剪切模量. Fig. 8 Computed results of well -logging data and theoretical models (a) Poission, ratio; (b) Calibrated factor of shear stiffness; (c) Combined parameters of R/R; (d)Bulk modulus; (e)Shear modulus. |
可使用Hertz-Mindlin、Digby 或Walton 等效介质模型计算干燥条件下具有随机堆积特征的等径球形颗粒集合体的弹性特征[1-3].这三个理论模型均以接触颗粒作为研究单元,在颗粒体积微元应力-应变本构基础上通过适度均匀化处理得到等效体积及剪切模量随介质孔隙度、围限压力及组成颗粒弹性性质的变化关系,仅在均匀化过程中处理颗粒接触面力学特征对介质剪切模量的影响上存在差异.上述等效介质模型均构建在均匀应变假设基础上的,即接触颗粒在微细观(颗粒)尺度上的应变特征与颗粒集合体的宏观应变特征一致.对颗粒集合体的离散元数值模拟表明,在单轴压缩下颗粒在细观尺度上应力和应变的方向基本是一致的(图 2b),虽然应变是不均匀的但并没有形成明显的由接触颗粒相对滑动等形成的应力松弛作用,微细观(颗粒)尺度的不均匀应变可由均匀应变近似,此时利用Hertz-Mindlin等效介质模型计算的颗粒介质体积模量与实际测量结果差异不大;而在纯剪压缩中,颗粒位移在细观尺度上反映出存在的相对滑动、转动、重排列等非线性运动,微细观尺度上的应变特征与颗粒集合体的宏观应变特征不一致,不再符合等效介质模型的均匀应变假设,造成Hertz-Mindlin等效介质模型所给出的剪切模量理论计算值与实际测量结果之间出现较大偏差.Kruyt与Rothenburg利用最小势能原理严格证明了基于均匀应变假设条件下的等效介质模型给出的弹性模量值是颗粒集合体等效弹性模量的上限[18].
颗粒集合体的弹性性质与施加应力或应变的幅度存在明显的相关关系.本次工作在进行颗粒介质的离散元数值模拟时所施加的应变ε=0.5%,而地震、测井及超声实验中形成的应变ε 通常在10-5-10-6这样一个量级,该应变小于数值模拟所施加的应变.这样会存在问题,即在ε=0.5%下利用数值模拟所观察到的颗粒相对滑动等非线性运动是否在地震波或超声波应变下仍然存在.通过离散元数值模拟可以知道组成颗粒相对滑动等非线性运动所形成的“应力松弛"对颗粒集合体的等效弹性特征有明显的影响,而能否发生“应力松弛"的关键是所施加的应力或应变幅度在颗粒微观尺度上能否超过接触颗粒表面的静摩擦力使颗粒的相对滑动等非线性运动得以开启.地震波或超声波应变下岩石组成颗粒相对滑动能否开启一直存在争议,从光滑球形玻璃珠所构成的人工疏松颗粒集合体的实验结果可以看出,在压力小于5MPa时颗粒接触边界力学条件更接近于完全光滑接触(C=0),即在很小的超声波应变幅度下如ε-10-6,仍可能存在接触颗粒相对滑动等“应力松弛"的非线性行为.Prasad与Meissner通过对疏松粗砂粒集合体的速度及品质因子测量结果认为,由颗粒间相对滑动所形成的摩擦衰减作用在应变幅度ε为10-6下仍然是造成弹性波衰减的重要因素[19].Tittmann等的实验结果表明胶结砂岩的横波衰减在应变幅度小于10-6的情况下与所施加的应变幅度仍然存在明显的相关关系[20].Deng等对页岩所进行的超声波实验结果也表明,干燥条件下页岩表现出衰减各向异性的主导机制是裂隙面之间、粘土矿物颗粒之间的滑动摩擦和静摩擦所造成的相位的滞后所引起的弹性波衰减作用[21].从上述实验结果可以看出,在应变幅度ε 小于10-6的情况下颗粒相对滑动等非线性运动仍然可能发生.组成颗粒的排列形式、胶结类型及特征、颗粒形状和表面粗糙度、介质所受压力特征等也直接或者间接影响颗粒接触表面的力学特征,进而在微观上影响组成颗粒相对滑动等非线性运动发生的程度.
6 结论(1) 颗粒介质单轴压缩的离散元数值模拟结果表明,在细观尺度上的强力链、颗粒位移与宏观压缩方向(应力方向)一致,轴向应力增量(Δσzz )在松弛阶段相对于硬化峰值变化较小,即颗粒相对滑动、旋转、重排列等形成的应力松弛作用影响较弱,细观不均匀应变仍能近似符合等效介质模型的均匀应变假设,Hertz-Mindlin等效介质模型可给出较为准确的体积模量理论计算值.
(2) 颗粒介质纯剪压缩的离散元数值模拟结果表明,颗粒位移在细观尺度上具有明显的涡状结构特征,反映出颗粒在微观尺度上所存在的相对滑动、转动、重排列等非线性运动,剪应力增量(Δτ)也表现出明显的应力松弛作用的影响,等效介质模型的均匀应变假设不再适用,造成Hertz-Mindlin 等效介质模型所给出的剪切模量理论计算值出现较大偏差.
(3) 在压力小于2.5MPa时颗粒接触边界力学条件更接近于完全光滑接触(C=0),随压力增加颗粒接触面满足“焊接"接触条件的等效部分也逐渐增加,表现为实验测量结果所具有的C值不断增大.形成这种现象的主要原因是随围限压力的增加集合体组成颗粒间的“互锁"现象增强造成接触颗粒的接触面摩擦阻力增加,颗粒接触面逐渐偏离完全光滑接触,在相同的应变扰动下颗粒相对滑动等非线性运动减弱.
(4) 利用切向刚度校正因子C及组合参数R/R对Hertz-Mindlin等效介质模型进行理论修正,以考虑颗粒松弛作用及颗粒接触面不规则性对介质等效弹性模量计算结果的影响.实际运用结果表明校正后的等效介质模型可给出未固结碎屑砂岩准确的地震弹性特征理论计算值.
致谢感谢两位匿名评阅人对本文所提出的宝贵意见.
| [1] | Mindlin R D. Compliance of elastic bodies in contact. Journal of Applied Mechanics , 1949, 16: 259-268. |
| [2] | Walton K. The effective elastic moduli of a random packing of spheres. Journal. Mech. Phys. Solids. , 1987, 35(2): 213-226. DOI:10.1016/0022-5096(87)90036-6 |
| [3] | Winkler K W. Contact stiffness in granular and porous materials: comparison between theory and experiment. Geophysical Research Letters , 1983, 10: 1073-1076. DOI:10.1029/GL010i011p01073 |
| [4] | Zimmer M A, Prasad M, Mavko G, Nur A. Seismic velocities of unconsolidated sands: Part1-Presssure trends from 0.1 to 20 MPa. Geophysics , 2007, 72(1): 1-13. |
| [5] | Makse H A, Gland N, Johnson D L, et al. Granular packing: nonlinear elasticity, sound propagation and collective relaxation dynamics. Physical Review E , 2004, 70(061302): 1-19. |
| [6] | Johnson D L, Makse H A, Gland N, et al. Nonlinear elasticity of granular media. Physica B , 2000, 279: 134-138. DOI:10.1016/S0921-4526(99)00700-0 |
| [7] | Bachrach R, Dvorkin J, Nur A. Seismic velocities and Poisson's ratio of shallow unconsolidated sands. Geophysics , 2000, 65: 559-564. DOI:10.1190/1.1444751 |
| [8] | Cundall P A, Strack O D L. A discrete numerical method for granular assemblies. Geotechnique , 1979, 29(1): 47-65. DOI:10.1680/geot.1979.29.1.47 |
| [9] | Majaudar T S, Behringer R P. Contact force measurements and stress-induced anisotropy in granular materials. Nature , 2005, 23: 1079-1082. |
| [10] | 徐泳, 孙其诚, 张凌, 等. 颗粒离散元法研究进展. 力学进展 , 2003, 33(2): 250–260. Xu Y, Sun Q C, Zhang L, et al. Advances in discrete element methods for particulate materials. Advances in Mechanics (in Chinese) , 2003, 33(2): 250-260. |
| [11] | 孙其诚, 王光谦. 静态堆积颗粒中的力链分布. 物理学报 , 2008, 57(8): 4668–4674. Sun Q C, Wang G Q. Force distribution in static granular matter in two dimensions. Acta Physica Sinica (in Chinese) , 2008, 57(8): 4668-4674. |
| [12] | 陈颙, 黄庭芳. 岩石物理学. 北京: 北京大学出版社, 2001 . Chen Y, Huang T F. Rock Physics (in Chinese). Beijing: Peking University Press, 2001 . |
| [13] | Mavko G, Mukerji T, Dvorkin J. The Rock Physics Handbook: Tools for Seismic Analysis in Porous Media. New York: Cambridge University Press, 1998 : 106 -160. |
| [14] | Norris A N, Johnson D L. Non-linear elasticity of granular media. Journal of Applied Mechanics , 1997, 64: 39-49. DOI:10.1115/1.2787292 |
| [15] | Thornton C, Barnes D J. Computer simulated deformation of compact granular assemblies. Acta Mechanica , 1986, 64(1): 45-61. |
| [16] | Brilliantov, Spahn F, Hertzsch J, et al. Model for collisions in granular gases. Physical Review E , 1996, 53(5): 5382-5392. DOI:10.1103/PhysRevE.53.5382 |
| [17] | 邓继新, 韩德华, 王尚旭. 未固结砂岩地震弹性性质的岩石物理模型表征研究. 石油地球物理勘探. 2010 : 249 -235. Deng J X, Han D H, Wang S X. Rock physics modeling characteristic studies on seismic elastic properties of unconsolidated sandstone (in Chinese). 2010 : 249 -235. |
| [18] | Kruyt N P, Rothenburg L. Kinematic and static assumptions for homogenization in micromechanics of granular materials. Mechanics of Materials , 2004, 36: 1157-1173. DOI:10.1016/j.mechmat.2002.12.001 |
| [19] | Prasad M, Meissner R. Attenuation mechanisms in sands: laboratory versus theoretical (Biot) data. Geophysics , 1992, 57: 710-719. DOI:10.1190/1.1443284 |
| [20] | Tittmann B, Abdel-Gawad M, Salvado C. A brief note on the effect of interface bonding on seismic dissipation. Proceedings of the 12th Lunar and Planetary Science Conference, 1981: 1737-1745 |
| [21] | Deng J X, Wang S X, Han D H. The velocity and attenuation anisotropy of shale at ultrasonic frequency. J. Geophys. Eng , 2009, 6: 269-278. DOI:10.1088/1742-2132/6/3/006 |
 2011, Vol. 54
2011, Vol. 54