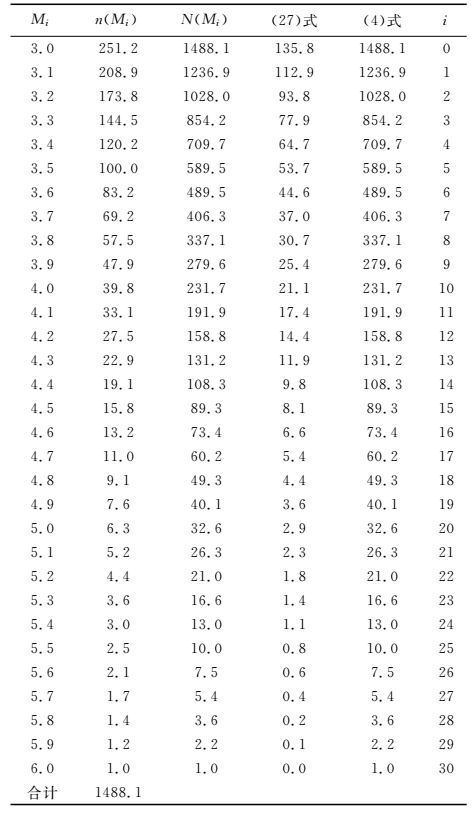
大小地震之间的著名统计关系为

|
(1) |
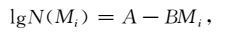
|
(2) |
式中,i= 0,1,2,…,k,其中,M0 为最小统计震级档,Mk为最大震级档.古登堡(Gutenberg)在统计时,将地震按震级分档,即n(Mi)是震级为Mi+ΔM的地震次数,为(1)式.里克特(Richter)采用按震级由强至弱累计(倒累计),即N(Mi)是震级大于等于Mi的地震次数,为(2)式.
刘正荣[1]和国家地震局震害防御司[2]均给出式(1)和式(2)中两常数的关系为
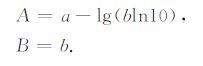
|
在实际工作中,一般情况下b>0.4343,则lg(bln10)>0,所以,a>A,而两式中斜率相等.这与实际情况不相符合,实际情况正好相反,而且,一般情况下b≠B.因此,有必要研究古登堡与里克特两种意义下震级频度关系的差异.
国内外学者[3~6]在研究地震的震级频度关系时广泛利用最大熵原理.本文也采用最大熵原理研究地震的震级频度关系,考虑到现实情况下地震的震级取值是离散的,本文通过离散求和方式进行相应的推演,而不是通过积分方式,并对相应结果进行实例验证.
2 震级离散条件下的震级频度关系(1) 式和式(2)的含义是有区别的,显然两种作法的结果有差异,那么,这两种理解有什么差别、有什么相同?
2.1 由古登堡震级频度关系得到里克特关系
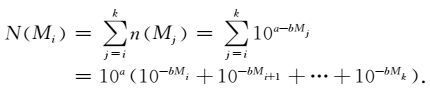
|
(3) |
因为N(Mi)为按震级由强至弱累计的地震次数,则总有N(Mi)≥1,即保证了对于每个Mi都有N(Mi)≥1的取值,由(3)式可知,N(Mi)是由(1)式确定的n(Mi)得到,这也保证了对于每个Mi,n(Mi)都有取值.因此(3)式的求和是最大最小震级档间的逐个震级档的求和.
设分档震级为ΔM,即ΔM= Mi+1 -Mi,亦有Mi+2 = Mi+2ΔM等等,则(3)式为

|
(4) |
对于同一组大小地震,给定震级分档为ΔM,且认为(1)式中a和b为常数,则有
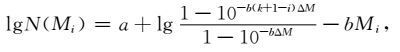
|
(5) |
与(2)式比较知
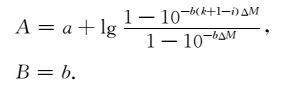
|
(6) |
当震级上限有限,当给定ΔM时,k也就确定了,此时,由于Mi=M0+iΔM,(6)式的第二项是与Mi有关的,即该项不是常数.即(5)式表达的里克特意义下震级频度关系不是直线.
因此,在震级上限有限时,里克特意义下的震级频度关系可能不是直线.
由(4)式并考虑到Mi= M0 +iΔM,可得
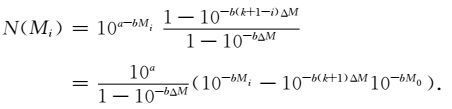
|
当给定ΔM,令k→∞,相当于震级上限取∞,此时上式取自然对数为
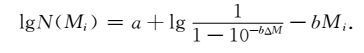
|
(7) |
与(2)式比较知
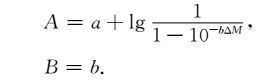
|
(8) |
此时,显然有a<A,这与实际情况正好相符合.同时注意到,两式中斜率相等,因此,在震级上限取∞时,里克特意义下的震级频度关系才是直线,此时也才有b=B.
2.2 最大熵原理与震级频度关系根据最大熵原理,利用拉格朗日未定乘子法,可求出熵极大时的震级频度分布.设随机变量M取M0,M1,… ,Mk,相应的概率为p0,p1,… ,pk.它们满足约束条件
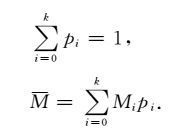
|
(9) |
为寻求在约束条件下熵极大时的分布,引入未定乘子α 和β,构造一个新函数H-α-βM,其中:$H = - C\sum\limits_{i = 0}^k {{p_i}} $lnpi是申侬(Shannon)定义的信息熵,pi是随机事件出现的概率,C是常数.则有
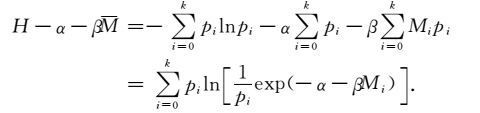
|
利用不等式lnx≤x-1(当x>0时),上式为
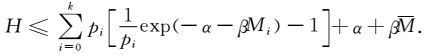
|
若要H取极大值,上式取等号,此时要求pk满足下式:
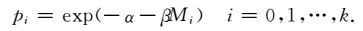
|
(10) |
设分档震级为ΔM,即ΔM= Mi+1 -Mi,亦有Mi+2 = Mi+2ΔM,Mi= M0 +iΔM等等,此时的约束条件也可表示为

|
(11) |
将(11)式代入(10)式,则震级概率分布函数为
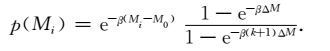
|
(12) |
将(12)式代入约束条件有
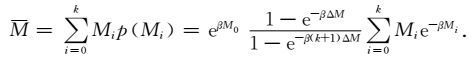
|
(13) |
式中求和项共有k+1项为

|
式中第二项求和共有k项,其中
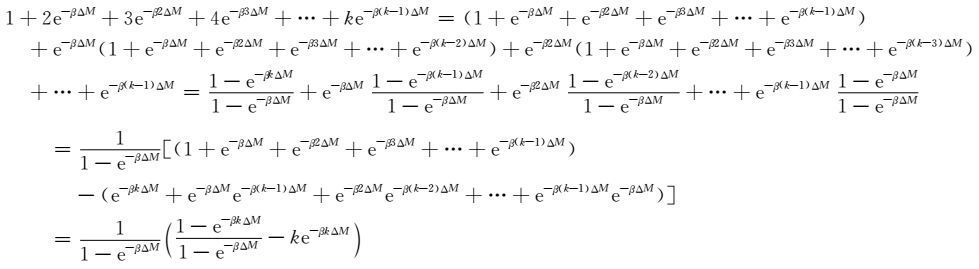
|
所以

|
(14) |
这里取$p\left( {{M_i}} \right) = \frac{{n\left( {{M_i}} \right)}}{N}$,其中,N为Mi≥ M0 的地震次数,即地震总次数,n(Mi)为震级为Mi的地震次数,即任何震级地震的发生只与其地震次数有关,则(12)式可表示为
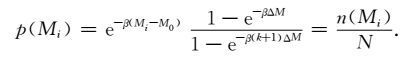
|
(15) |
(15) 式采用常用对数表示为

|
(16) |
(16) 式为古登堡意义的震级频度关系,相应的常数为
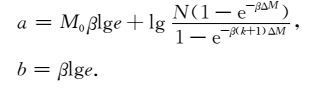
|
(17) |
里克特意义下的震级频度关系中,地震频次是按震级由强至弱累计,即为震级大于等于Mi的地震次数,记为N(Mi),则由(15)式得
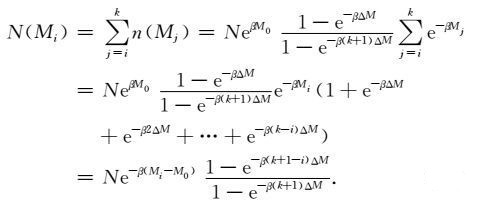
|
(18) |
(18) 式采用常用对数表示为
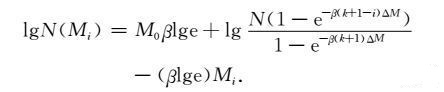
|
(19) |
(19) 式为里克特意义的震级频度关系,相应的常数为
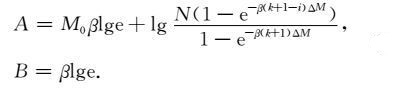
|
(20) |
对比(16)式和(19)式,当给定k和ΔM时,(17)式为常数;此时,由于Mi= M0 +iΔM,(19)式的第二项是与Mi有关的,即不是常数.
因此,在震级上限有限时,即当给定k时,ΔM也给定了,此时,(16)式为直线,(19)式不是直线.
当给定ΔM,让k→ ∞ 时,即Mk→ ∞,相当于震级上限取∞,(16)式和(17)式分别为
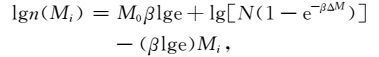
|
(21) |
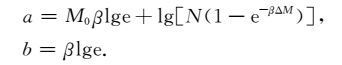
|
(22) |
(19) 式和(20)式为

|
(23) |
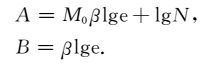
|
(24) |
此时(14)式为
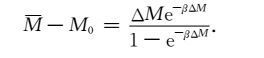
|
即
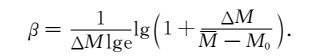
|
(25) |
对比(22)式和(24)式,在震级上限取∞ 时,里克特意义下的震级频度关系才是直线,此时也才有b=B.
(12) 式(震级概率分布函数)给出当震级为Mi时的概率p(Mi),如果要求当震级大于等于Mi时的概率,即累积频度震级概率分布函数P(Mi)应为

|
(26) |
如果取$P\left( {{M_i}} \right) = \frac{{N\left( {{M_i}} \right)}}{N}$,其中N为Mi≥ M0的地震次数,即地震总次数,N(Mi)为震级大于等于Mi的地震次数,即倒累积地震频度,则(26)式与(18)式为同一表达式.
通过(4)式与(18)式均可得到N(Mi),注意到(17)式中的b=βlge, 并且N=N(M0),则由(4)式可以得到(18)式,即(4)式与(18)式是相同的.
3 实例验证本文通过实例验证两个问题:(1)震级大于等于Mi的地震次数N(Mi)的求法,即倒累计地震次数的求法;(2)倒累计地震次数与震级的线性关系.
3.1 倒累计地震次数的求法验证在由震级为Mi的地震次数n(Mi)求震级大于等于Mi的地震次数N(Mi)时,(4)式是按分档震级的方式(离散方式)求和;同时经常也可看到:设lgn(Mi)=a-bMi为连续且可积函数,然后通过n(Mi)积分
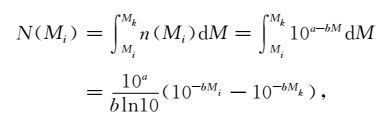
|
(27) |
得到N(Mi),并认为N(Mi)是震级大于等于Mi的地震次数.下面以实例lgn(Mi)= 4.8-0.8Mi验证:(27)式得到的N(Mi)不是震级大于等于Mi的地震次数.
设一组地震按lgn(Mi)=4.8-0.8Mi取值,为便于计算设M0 =3.0、ΔM=0.1,则Mk=6.0、k=30,表 1第1列由(1)式得到、第2列由第1列数据按震级由大到小累加得到,由表 1可知:(27)式得到的结果是错误的,(4)式得到的结果是正确的.原因可能是:假设lgn(Mi)=a-bMi为连续且可积函数是错误的,因为Mi的取值是离散的,而不是连续的.
3.2 倒累计地震次数与震级的线性关系验证由表 1第1列数据和3列取自然对数的数据,当i取不同值时,即取不同的震级下限,通过线性最小二乘法方法进行拟合,得到相应统计结果(见表2).从统计的角度看:i取不同值,线性拟合均能通过信度检验,线性拟合是成立的.同时可以发现:随着i取值增加,a值和b值出现一致的增大变化,并没有稳定的值出现,即a值和b值的取值与震级下限有关.
|
|
表 1 累积地震次数3种算法的实例验证 Table 1 The case verification of the 3 calculations for cumulative earthquake number |
|
|
表 2 累计地震次数与震级的线性最小二乘法拟合结果 Table 2 The fitting results of linear least square method for cumulative earthquake number and magnitude |
对于古登堡意义的震级频度关系,由表 1 第1和2列的数据,对于i取不同的值,通过线性最小二乘法方法进行拟合,均能得到相同的统计结果.由表 1第1、2列数据可得M=3.484103,代入(14)式得β=1.842068,代入(17)式得a=4.8、b=0.8,即根据表 1第1、2 列,按最大熵原理可得到古登堡意义的震级频度关系(1)式.这验证了(4)式与(18)式是相同的.
4 结论与讨论本文通过理论研究和实例验证的方式,探讨震级离散条件下两种震级频度关系的异同,希望能引起地震活动性相关研究和应用的重视.事实上,实际工作中震级就是离散的,因此两种震级频度关系存在重大差别,在实际应用中应该考虑两者的差异.
在现实震级离散的情况下,震级大于等于某一震级的地震次数应通过离散求知的方式得到,而不应通过积分的方式得到.
震级上限取为∞ 的情况下,古登堡和里克特意义的震级频度关系式是直线,此时才有b=B,而a<A.在震级上限有限的情况下,里克特意义下的震级频度关系可能不是直线,即按震级由强至弱累计得到的累积频次的常用对数lgN(Mi)与震级Mi的关系可能不是直线.实例验证进一步证实,该震级频度关系式的系数值与震级下限有关.
本文给出的震级概率分布函数,参数β =blge的b值由古登堡意义的震级频度关系得到,而不是由里克特意义的震级频度关系得到.
在地震活动性方面,总结了许多地震活动的经验公式,公认的并在实际观测中获得证实,且具有一定普遍性的现象并不多,其中古登堡-里克特公式是能被大家基本接受的.本文是从古登堡意义下的震级频度关系推出里克特意义的震级频度关系,并不是直接得到里克特意义的震级频度关系.而在实际工作中,古登堡和里克特震级频度关系均能通过信度检验,线性拟合是成立的.
| [1] | 刘正荣. b值特征的研究. 地震研究 , 1995, 18(2): 168–173. Liu Z R. Feature studies of b value. Joural of Seismological Research (in Chinese) , 1995, 18(2): 168-173. |
| [2] | 国家地震局震害防御司. 地震工作手册. 北京: 地震出版社, 1992 : 276 -281. Department of Earthquake Disaster Prevention China Earthquake Administration. Handbook for Seismological Research (in Chinese). Beijing: Seismological Press, 1992 : 276 -281. |
| [3] | Berril J B, Davis R O. Maximum entropy and the magnitude distribution. Bull. Seism. Soc. Am , 1980, 70: 1823-1831. |
| [4] | Dong W M, Bao A B, Shah H C. Use of maximum entropy principle in earthquake recurrence relationships. Bull. Seism. Soc. Am. , 1984, 74: 725-737. |
| [5] | Jichun Sun, Tso-Chien Pan. The probability of very large earthquakes in Sumatra. Bull. Seism. Soc. Am , 1995, 85: 1226-1231. |
| [6] | 冯利华. 最大熵原理与地震震级-频度关系. 地震地质 , 2003, 25(2): 260–265. Feng L H. Maximum entropy principle and seismic magnitude frequency relation. Geology and Seismology (in Chinese) , 2003, 25(2): 260-265. |
 2011, Vol. 54
2011, Vol. 54