2. 中国科学院动力大地测量学重点实验室,武汉 430077;
3. 中国科学院研究生院,北京 100049
2. Key Laboratory of Dynamical Geodesy, Institute of Geodesy and Geophysics,CAS, Wuhan 430077, China;
3. Graduate University of the Chinese Academy of Sciences, Beijing 100049, China
物理大地测量学的理论与实践表明,由于地球重力场及时变是由地球表层及内部物质的空间分布、运动和变化决定的,因此精确确定地形起伏至关重要,如地面、海洋和航空重力数据的归算和格网化(拟合推估),利用移去-恢复技术联合地面重力数据、航空重力数据、数字地形模型(DTM)和全球重力场模型高精度确定局部大地水准面等.此外,应用Stokes 公式计算的前提是大地水准面外部不存在质量,这就要求移去大地水准面以外地形质量的影响[1].因此研究局部地形改正具有重要意义.
尽管已有许多学者对局部地形改正进行过研究[2~8],但是就局部地形改正积分核函数的奇异问题仍需做进一步探讨.为此,本文在已有的基础上,提出了利用高斯积分法[9]以及在积分式中的奇异性核函数加入一常数项两种方法来克服地形改正公式的奇异性问题,并推导了高斯积分法处理奇异积分的公式及含可选小常数的地形改正的严密级数展开式.由于积分的奇异性经过数学上的技巧加以消除,求解时不再需要假设形状函数,因此计算的地形改正的精度优于柱状体积分法[1]的精度.
同时,文中采用最新公布的分辨率为3″×3″的SRTM3[10]地形数据代替常用的分辨率为30″×30″的GTOPO30数据计算局部地形改正,提高了地形信息的利用率.结合实际算例确定了地形改正的级数展开式的可选次项和最佳常数以及高斯积分法的最佳内外圈半径,并详细讨论了两种奇异积分处理方法和两种分辨率的地形数据对地形改正的影响.
2 克服地形改正奇异积分的方法相对于点P(xp, yp, hp),不规则地形起伏产生的引力位为[11]
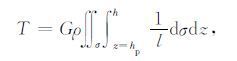
|
(1) |
式中l= [(x-xp)2 + (y-yp)2 + (z-zp)2]1/2,G为牛顿引力常数,ρ 为地壳密度(假设为常数),x、y、h为流动点的坐标及高程,xp、yp、hp 为计算点的坐标及高程.式(1)的负垂直方向分量可得重力的地形改正:
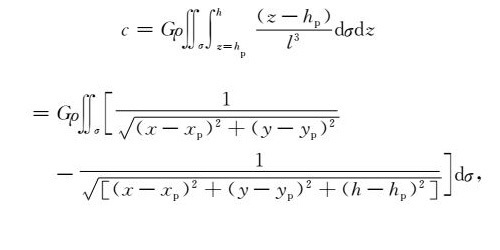
|
(2) |
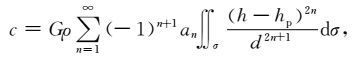
|
(3) |
式中
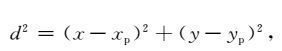
|
(4) |
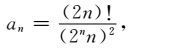
|
(5) |
当n只取n=1时,式(3)可利用FFT 法计算,写成谱形式[14~16]为
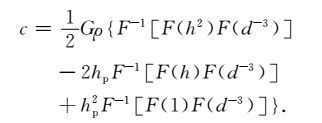
|
(6) |
在计算点处(即d-3 → ∞),核函数出现奇异现象.为了解决这个问题,本文引入高斯积分法与核函数项增加常数因子法两种方法来解决这一问题.下面推导高斯积分法处理奇异积分的公式及含可选小常数的地形改正的严密级数展开式.
2.1 地形改正的高斯积分法由于式(2)中的核函数在某些点(当x=xp、y=yp时)是奇异的,国内外众多学者[17~19]对奇异点积分的问题都进行过研究.我们采用高斯积分法解决这个问题.
在P点附近,高程可以泰勒展开成
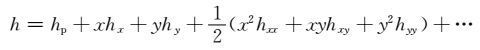
|
(7) |
其中,${h_x} = \frac{{\partial h}}{{\partial x}},{h_y} = \frac{{\partial h}}{{\partial y}},{h_{xx}} = \frac{{{\partial ^2}h}}{{\partial {x^2}}},{h_{xy}} = \frac{{{\partial ^2}h}}{{\partial x\partial y}},{h_{yy}} = \frac{{{\partial ^2}h}}{{\partial {y^2}}}$.内圈的地形质量影响可用以P点为原点,s0 为半径的圆来表示.采用极坐标(r,α),令x=rsinα,y=rcosα,则式(2)可写成
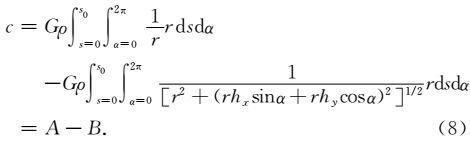
|
(8) |
积分后,A项:
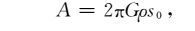
|
(9) |
利用三角函数公式,B项为

|
(10) |
式中,$a = \sqrt {h_x^2 + h_y^2} ,\theta = \alpha + \arctan \frac{{{h_y}}}{{{h_x}}}$.令$\beta = \frac{\pi }{2}$-θ,(10)式可写为
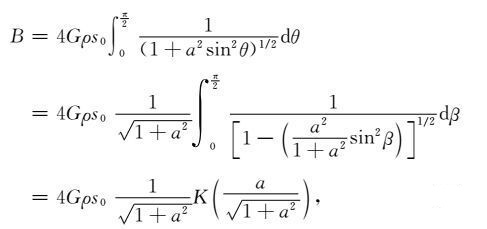
|
(11) |
其中,$K\left( \kappa \right) = \int_0^{\frac{\pi }{2}} {\frac{{d\beta }}{{\sqrt {1 - {\kappa ^2}{{\sin }^2}\beta } }}} $,可利用完全椭圆积分公式求解[20].
若给定的高程数据是以ΔΦ×Δλ 划分的网格数据,则内圈半径可近似为
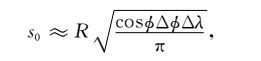
|
(12) |
R为地球半径(≈6371km),Φ 为纬度.
2.2 含常数因子的地形改正严密级数展开式为了克服式(3)中核函数的奇异问题,亦可在核函数项增加一常数因子α,使用新的水平距离函数d1(x,y)代替原来的d(x,y)函数,即令

|
(13) |
式(13)中,α 为非零小常数.这样做不但可以克服核函数在计算点处的奇异性,而且可以通过适当选取α 值,使式(3)级数展开满足条件:
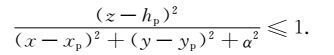
|
(14) |
通过一定的变换,可以推出含可选小常数α 的计算地形改正数的严密级数展开式.首先将式(1)中的l改写为
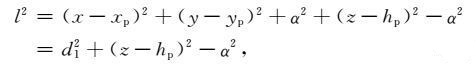
|
(15) |
将(15)式代入式(2),得
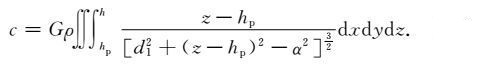
|
(16) |
设${\left( {\frac{{\sqrt {{{\left( {z - {h_p}} \right)}^2} - {\alpha ^2}} }}{{{d_1}}}} \right)^2} \le 1$,根据式(3)可得出[1]
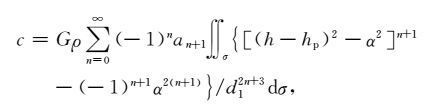
|
(17) |
当n=0时,有
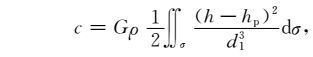
|
(18) |
当n取0和1两项时,有
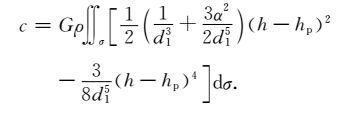
|
(19) |
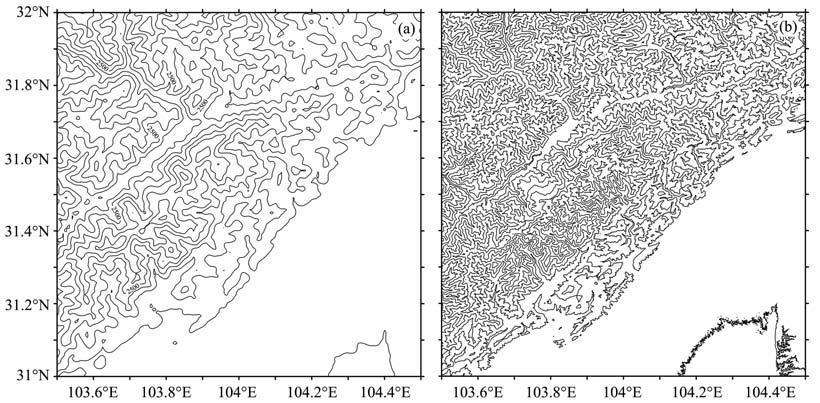
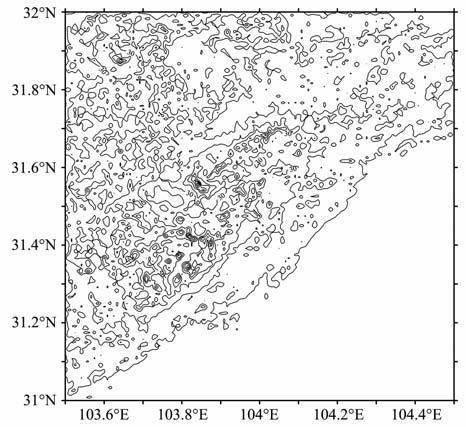
为了研究不同分辨率的地形数据对地形改正的影响,本文搜集了31°N~32°N,103.5°E~104.5°E区域分辨率为30″×30″的GTOPO30 和分辨率为3″×3″的SRTM3地形数据.图 1给出了计算区域内两种地形数据的等值线图.GTOPO30 高程最大值为4616.75m, 平均为1692.96m;SRTM3高程最大为4949.99m, 平均为1969.10m.GTOPO30与SRTM3地形数据在该地区的差异,最大为330 m, 平均相差13m, 标准差为7.7m.
|
图 1 地形数据(单位:m) (a)GTOPO30 (间距:500m);(b)SRTM3 (间距:500m). Fig. 1 Topographic data (unit: m) |
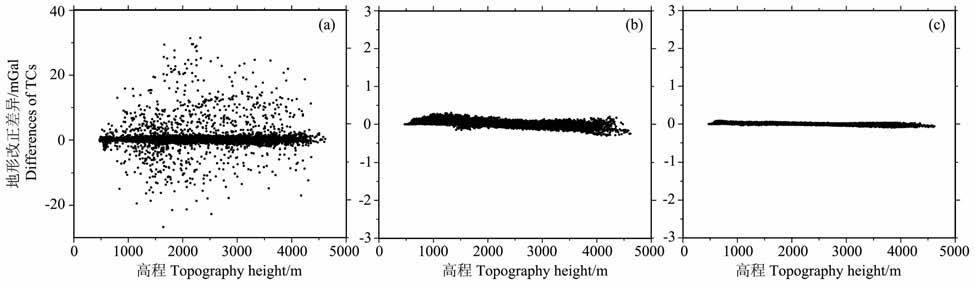
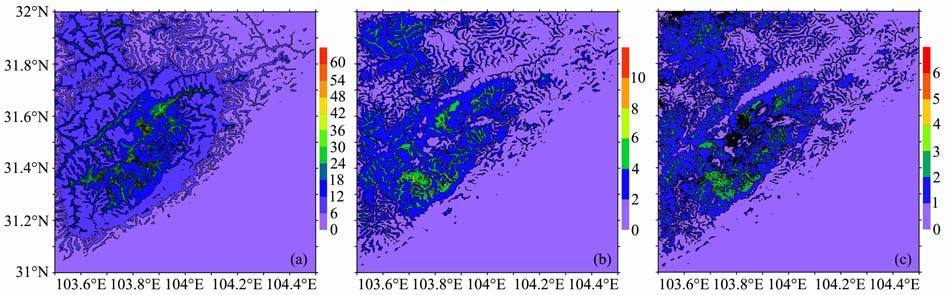
实际应用中,采用3″×3″的格网地形数据计算内圈的地形影响,采用30″×30″的格网地形数据计算外圈的地形影响.首先讨论内圈半径的选取.我们将外圈半径固定为60km.图 2表示了用两种不同的内圈半径计算的地形改正的差异.由图可见,应选择20km 为最优内圈半径值.对外圈半径的选取采用同样的方法,将内圈半径固定为20km, 分析比较外圈半径选为30km 和50km、50km 和100km、100km 和150km 时地形改正值的差异,以选择最优外圈半径值.从图 3 可以看出在外圈半径选为30km和50km、50km 和100km 的情况下,两者的差异随着高程的增加而增加.为了保证地形改正达到0.5mGal的精度,外圈半径不得小于100km.
|
图 2 两种内圈半径计算的地形改正差异 (a)2km 和10km;(b)10km 和20km;(c)20km 和30km. Fig. 2 Difference in TCs using two different radii of inner zone |

|
图 3 两种外圈半径计算的地形改正差异 (a)30km 和50km;(b)50km 和100km;(c)100km 和150km. Fig. 3 Difference in TCs using different radii of outer zone |
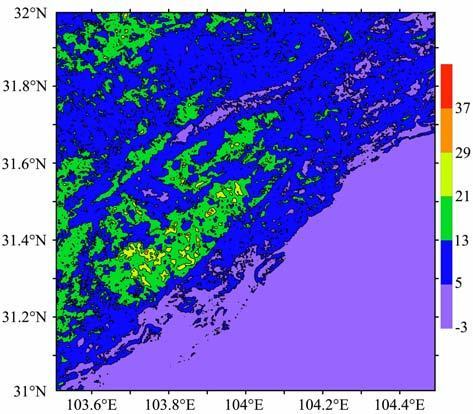
为了提高计算速率并保证仍有0.5mGal的精度,该区域的最佳内外圈的半径分别采用20km 和100km.如图 4 所示,地形改正值一般与高程成正比,地形改正最大值出现在海拔为4923 m 的地区,并且其最大值为99.65mGal, 最小值为0.15mGal, 平均15.39mGal.
|
图 4 高斯积分法得到的地形改正(单位:mGal) Fig. 4 TCs using Gaussian quadrature method (unit: mGal) |
常数α 的选取:为了比较式(13)常数α 选值不同对精度的影响.这里我们采用四种方案进行实验:(Ⅰ)α=高程平均值;(Ⅱ)α=高程最大值-高程最小值;(Ⅲ)α=高程标准偏差;(Ⅳ)α=高程标准偏差/sqrt(2).采用SRTM3 数据,计算至一次项.因试算区域本身较小,没有考虑积分半径,尽可能使用全部数据,因此下面所有积分运算均是对整个计算区域积分.
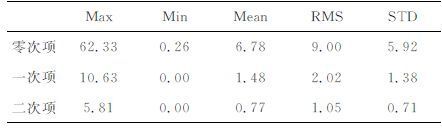
表 1给出了不同方案的α 值及各方案得到的地形改正与高斯积分结果的差异.从理论上讲,常数的选取宜小不宜大.表 1的结果也表明,当常数α 选第四种方案,即α= 高程标准偏差/sqrt(2)时,计算的地形改正与高斯积分法计算结果最为接近.故该计算区域的常数应选取方案Ⅳ.
|
|
表 1 选择不同常数计算的地形改正与高斯积分结果的比较 Table 1 Comparison of TCs calculated with different constants and Gaussian quadrature |
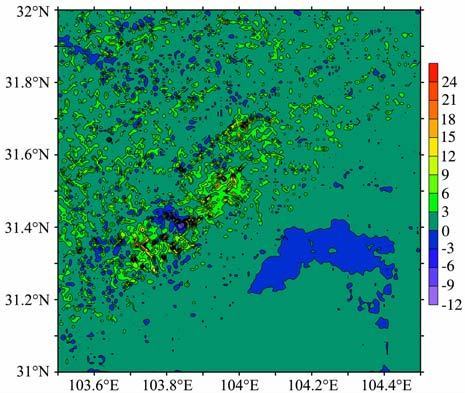
截断误差的影响:对于前面列出的计算模型(式(17)),我们分别计算了当计算模型只取零次项(只顾及到d13)时地形改正结果以及一次项(对应于d15)和二次项(对应于d17)对地形改正结果的影响.地形数据使用SRTM3 数据,具体试验结果如表 2和图 5所示.从计算结果可以看出,地形改正量大小及计算模型一次项和二次项对计算结果的影响大小均明显与计算区域高程变化的剧烈程度有关.在比较平坦的地区,计算模型一次项和二次项对计算结果的影响均小于2mGal, 在实际应用中可不考虑其影响;而在地形变化比较剧烈的地区,一次项和二次项的影响可达平坦地区的几倍,在这些地区,应考虑将计算模型扩展到二次项.就地形改正数本身而言,对于试验区的地形条件,在重力场逼近计算中,都应当顾及地形效应的作用,并且这项改正明显呈系统性影响,在大地水准面计算中更应当引起重视.
|
图 5 截断误差对地形改正的影响(单位:mGal) (a)计算至零次项;(b)计算至一次项;(c)计算至二次项. Fig. 5 Effects of the truncation error on TCs (unit: mGal) |
|
|
表 2 截断误差对地形改正的影响(单位:mGal) Table 2 Effects of the truncation error on TCs (unit: mGal) |
为了比较高斯积分法和含可选小常数的级数展开法对地形改正计算的影响,本文分别利用这两种方法进行试算,数据采用SRTM3.对于高斯积分,内外圈半径分别选20km和100km, 计算地形改正cz ;对于级数展开法,常数α= 高程标准偏差/sqrt(2),计算至二次项,得到地形改正cz.图 6给出了两种方法得到的地形改正的差值,平均相差3.87mGal.从图也可以看出两者的差值与地形有很强的相关性.
|
图 6 高斯积分法和级数展开法计算的地形改正差值(单位:mGal) Fig. 6 Difference of TCs using Gaussian quadratureand series expansion (unit: mGal) |
|
图 7 SRTM3和GTOPO30数据计算的地形改正差异(单位:mGal) Fig. 7 Difference of TCs using SRTM3 and GTOPO30 (unit: mGal) |
SRTM3和GTOPO30不同之处是,SRTM3是表示地面上物体最高处的高程,在裸露地面(含水面),SRTM3所表示的高程和GTOPO30 一致;地面上若有建筑物、植物或其他附着物,则SRTM3所表示的高程就是地面附着物顶部的高程.为了比较两者对计算地形改正的影响,本文分别用这两组数据计算地形改正,采用级数展开法计算至二次项.图7的结果表明,由于低分辨率地形数据损失了部分高频信息,使得由两种分辨率的地形资料计算的地形改正的差异较大.此项误差在厘米级大地水准面的确定中不容忽视.地形变化越剧烈的地区这种影响也越大.该试算结果说明,对于山区局部地形的计算应尽可能采用较高分辨率的地形数据.
4 结论本文详细介绍了高斯积分法及级数展开法在局部地形改正中的应用,并推导了地形改正的奇异积分处理公式和含可选小常数α 的计算地形改正数的严密级数展开式.同时采用最新公布的SRTM3 地形数据代替常用的低分辨率的GTOPO30数据计算地形改正,通过实际的算例分析,可得出如下结论:
(1) 在局部地形改正计算中引入高斯积分法和含可选小常数级数展开法,可以有效地克服地形改正积分核函数的奇异问题,并且不影响地形改正计算的精度.
(2) 对于高斯积分法,为了提高计算速率并保证仍有0.5mGal的精度,本文计算区域的最佳内外圈的半径分别为20km 和100km;此结论是否适用其他地区数据尚需另作分析.尽管对于不同地区的地形改正计算内外圈半径选取可能有所不同,但是研究内外圈半径对计算精度的影响这步工作是必需的.
(3) 对于地形改正级数展开法,地形改正量大小及计算模型一次项和二次项对计算结果的影响大小均明显与计算区域高程变化的剧烈程度有关.并且当核函数中的常数取α=高程标准偏差/sqrt(2)时,计算的地形改正值与高斯积分法的计算结果最为接近.
(4) 利用GTOPO30 与SRTM3 两种数据计算的地形改正,最大相差25 mGal, 且地形变化越激烈,两者之间的差异越大.因此,在局部地形改正计算中,尤其在地形变化复杂地区应尽量采用高分辨率的SRTM3数据.
| [1] | Moritz H. Advanced Physical Geodesy. Tunbridge Wells Kent, England: Abacus Press, 1980 . |
| [2] | 许厚泽. 我国精化大地水准面工作中若干问题的讨论. 地理空间信息 , 2006, 4(5): 1–3. Xu H Z. Some problems on the precise determination of regional geoid in China. Geospatial Information (in Chinese) , 2006, 4(5): 1-3. |
| [3] | Li Y C. Optimized spectral geoid determination. UCGE Report No. 20050, Department of Geomatics Engineering, The University of Calgary, Calgary, Alberta, 1993 |
| [4] | Schwarz K P, Sideris M G, Forsberg R. The use of FFT techniques in physical geodesy. Geophysical Journal International , 1990, 100: 485-514. DOI:10.1111/gji.1990.100.issue-3 |
| [5] | Sideris M G, Li Y C. Gravity field convolutions without windowing and edge effects. Bulletin Geodesique , 1993, 67: 107-118. DOI:10.1007/BF01371374 |
| [6] | Sideris M G. A fast Fourier transform method of computing terrain corrections. Manuscripta Geodaetica , 1985, 10(1): 66-73. |
| [7] | Sideris M G. Rigorous gravimetric terrain modeling using Molodensky's operator. Manuscripta Geodaetica , 1990(15): 97-106. |
| [8] | Novák P, Vaníek P, Martinee Z, et al. Effects of the spherical terrain on gravity and the geoid. Journal of Geodesy , 2001, 75: 491-504. DOI:10.1007/s001900100201 |
| [9] | 周鼎赢. 以非奇异性暇积分改善三维边界积分法. 台湾:国立台湾大学,2005. Zhou D Y. An innovation of 3-D non-singular boundary integral equations (in Chinese)., Taiwan: National Taiwan University, 2005 |
| [10] | 陈俊勇. 对SRTM3和GTOPO30地形数据质量的评估. 武汉大学学报(信息科学版) , 2005, 30(11): 941–944. Chen J Y. Quality evaluation of topographic data from SRTM3 and GTOPO30. Geomatics and Information Science of Wuhan University (in Chinese) , 2005, 30(11): 941-944. |
| [11] | 李建成, 陈俊勇, 宁津生, 等. 地球重力场逼近理论与中国2000年似大地水准面的确定. 武汉: 武汉大学出版社, 2003 . Li J C, Chen J Y, Ning J S, et al. The thoery of Earth gravity field approximation and determination of 2000 qusi-geoid (in Chinese). 2003 . |
| [12] | Jon Kirby, Will Featherstone. High-resolution grids of gravimetric terrain orrection and complete Bouguer corrections over Australia. Exploration Geophysics , 2002, 33: 161-165. DOI:10.1071/EG02161 |
| [13] | Heiskanen W A, Moritz H. Physical Geodesy. San Francisco and London: W H Freeman Co., 1967 |
| [14] | Martinec Z, Vaníc?k P, Maínville A, et al. Evalution of topographical effects in precise geoid computation from densely sampled heights. Journal of Geodesy , 1996, 70: 746-754. DOI:10.1007/BF00867153 |
| [15] | Sideris M G, Tziavos I N. FFT evaluation and applications of gravity field convolution integrals with mean and point data. Bull. Geod , 1988, 62: 521-540. DOI:10.1007/BF02520242 |
| [16] | Sideris M G. Computation of gravimetric terrain corrections using fast Fourier transform techniques. USCE Report No. 20007, Department of Surveying Engineering, The University of Calgary, Calgary, Alberta, 1984 |
| [17] | Schwarz K P, Sideris M, Forsberg R. The use of FFT techniques in physical geodesy. Geophysical Journal International , 1990, 100: 485-514. DOI:10.1111/gji.1990.100.issue-3 |
| [18] | Tsoulis D. Terrain correction computations for a densely sampled DTM in the Bavarian Alps. Journal of Geodesy , 2001, 75: 291-307. DOI:10.1007/s001900100176 |
| [19] | Bian S, Sun H. The expression of common singular integrals in physical geodesy. Manuscripta Geodaetica , 1994, 19: 62-69. |
| [20] | Lebedev N N. Special Functions and their Applications. New York: Dover Publication, 1972 . |
 2011, Vol. 54
2011, Vol. 54