日食为研究低电离层受太阳的控制作用提供了很好的机会.迄今为止,我国已经开展了十多次日食电离层观测工作,积累了宝贵的观测资料,分析了日食电离层效应,并模拟与研究其物理过程与机制,对日地环境的耦合研究、日食现象中的电波传播科学与技术问题研究等产生了积极影响[1, 2].以前的研究主要集中在观测电离层的日食效应[3],主要研究的对象是F2 层临频和TEC(总电子含量)在日食期间的变化规律[4, 5],曾经也有学者尝试通过电离层理论模式来解释日食期间观测到的现象[6]和分析日食期间的电离层响应[7- 10],同时由日食激发的重力波的传播也是一个研究的热点问题[11].还有学者利用长波传播试验研究过电离层D 区在日食期间的变化[12],其中研究的主要问题一方面是日食期间D区电离层的变化特征[13, 14],另一方面是日食对于长波通信的影响[15],不过针对中高层大气的日食效应的观测研究相对较少,尤其是在理论分析和模型计算方面,这可能与该区域的观测比较困难有关.
2009年7月22日发生的日全食是在我国500年一遇的持续时间最长、日全食见食时间最长、覆盖地域最广的一次日全食.长江流域大部分地区全食时间可达到3~5 min 左右,在太平洋的2413′N,11407′E 点日全食最长持续时间达6m39s.全食带覆盖了我国长江流域的广大地区,其他地区也可观测到食分不同的偏食,这为观测与研究日食电离层效应提供了实验条件和机会.本文利用昆明站中国电波传播研究所新引进的MF(Median Frequency)雷达对2009年7月22日昆明站日偏食期间的D 区电子密度进行观测,讨论昆明站上空D 区的电离层效应,并基于两个简单的模型对D 区的有效复合系数进行了估算.本文第2 节介绍了日食分析数据的选取及分析方法,第3 节讨论了电子密度的日食效应并利用电子产生率和电子密度的关系对有效复合系数αeff进行建模估算,第4节给出结论,验证假设的合理性.
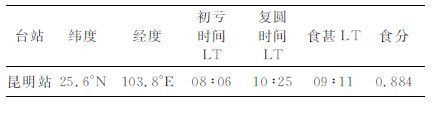
2 数据及分析方法昆明观测站位于(25.6°N,103.8°E),根据NASA 关于2009年7月22日这次日食的报告,昆明站发生的是日偏食,食分为0.884,其中初亏时间为08∶06LT,复圆时间为10∶25LT,食甚时间为09∶11LT,日食参数见表 1.
|
|
表 1 日食观测主要参数 Table 1 Main parameters during eclipse |
昆明MF 雷达选择FCA (Full Correlation Analysis)与DAE(Differential Absorption Experiment)交替进行的模式来探测D 区50~100km 高度的大气参数,工作频率是2.138 MHz, 其中前两分钟采用FCA 模式观测中层大气风场,后一分钟采用DAE 模式观测中层电子密度,一个运行周期为3min.DAE 观测主要实验参数见表 2.探测电子密度时,雷达交替发射O 波和X 波,由于MF 雷达天线能够分辨下行波的O 波与X 波,通过测量两个特征波的振幅与相位可以得到电子密度等信息,因此,每3min可以提供一组电子密度高度剖面,其中垂直高度分辨率为2km.在64km 以下,由于偏移吸收很弱,电子密度观测结果不可靠;而在84km 以上的DAE 观测存在众多的不确定性,这给电子密度的测量带来了很多误差,结果也不可靠[16].因此,本文选取昆明站在日食期间的DAE 观测结果,分析70~80km 高度上的电离层日食效应.
|
|
表 2 昆明站MF雷达DAE观测主要参数 Table 2 Main parameters of the DAE measurement of MF radar at Kunming station |
Gardner和Pawsey的DAE 方法利用电离层D区X 波与O 波的回波振幅比Axo反演电子密度.海拔高度为h处的回波振幅比可以表示为
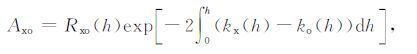
|
(1) |
这里Rxo(h)是高度h处X 波与O 波反射系数的比值,kx(h)和ko(h)分别是X 波与O 波的吸收系数.如果我们能够观测到h1 和h2 处的振幅比,而h1 和h2 之间的Δh又很小,就可以认为kx 和ko 保持为常数.于是由公式(1)可以得到
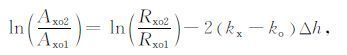
|
(2) |
其中Axoi和Rxoi,i=1,2,分别为hi处的振幅比和反射系数比.利用菲涅耳反射是基于电子密度波动的假设,通过假设的电子密度Ne(h)和碰撞频率vm(h)可以计算得到Rxoi.方程表示如下[17]:
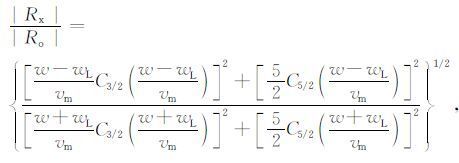
|
(3) |
式中,w=2πf,f为工作频率;wL =2πfHcosθ,fH是磁旋频率,θ 是电波传播方向与地磁场的夹角;vm是碰撞频率;C3/2 和C5/2 是两个积分[18].利用Appleton-Hartree磁离子理论再结合公式(2),电子密度Ne(h)就可以用Rxoi和kx(h)、ko(h)之间的关系来表示[19].在上面这些公式的推导过程中假设了碰撞频率与电子密度是相互独立的,因此可以忽略电子速度的分布.
然而,在D 区和E 区下部当碰撞频率足以可以与角波频率相比较时,对于中频传播,上边的假设对该区域就不成立了.因此DAE 要通过通用的磁-离子方程来改进.Sen-Wyller方程随后被后来的研究学者所采纳.为了求解特定高度hi处的电子密度Ne, 对方程(2)求导:
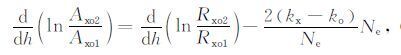
|
(4) |
所有的量均是在hi求得的,i=1,2.对于电子密度,
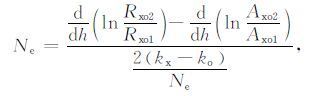
|
(5) |
式(5)即为DAE 求取电子密度的核心公式.
事实上,实验结果是在有限差分高度内通过比较测量方法得到的,反射系数则是根据碰撞频率剖面和不规则体结构的模型来估算得到的.但理论上在差分吸收kx 和ko 非常小的情况下,kx 和ko 应该是趋于零的,则方程(2)就变为
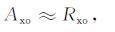
|
(6) |
这个方程可以用来决定D 区的碰撞频率.
关于碰撞频率的表达式很多,而给定大气压强p后的一个常用表达式为[20]
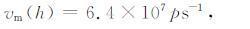
|
(7) |
式中p为压强,单位为Pa.方程(7)是一个经验表达式,该表达式是通过对涉及到电子和中性气体分子之间碰撞的各种要素的传输横截面的实验室最佳实验方法推理得到的,比如氮和氧分子、氧原子之间的碰撞.
然而,最新得到的大气气体中电子迁移率的实验室研究结果对氮气碰撞横截面进行了大幅修正.利用CIRA-86 中提供的大气温度和大气密度(压强)数值就有可能在弱等离子体中计算出电子与中性气体分子之间的平均迁移碰撞频率[21],表达式如下:

|
(8) |
k是玻耳兹曼常数,N是气体密度数,单位是m-2,E是电子能量,T是大气温度,σ是气体分子迁移碰撞横截面,m是电子质量.N0 和σ0 是规范常数,N0σ0 =1.用氮气要素迁移碰撞横截面的最新实验室观测结果[21],结合先前的氧分子和氧原子数据[22, 23],再根据方程(8)就可以计算出碰撞频率.除非有特殊说明,所有的电子密度都是由方程(8)得到的碰撞频率估计得到的.
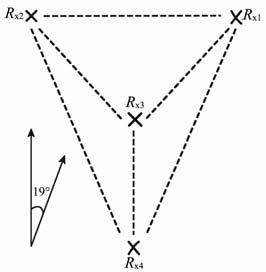
昆明MF雷达采用典型的分布式天线(SA),由4幅交叉偶极子天线按等边三角形布局组成收发共用天线阵,三幅天线分布在等边三角形的三个角上,另外一幅天线位于三角形的中心,其中三幅天线与另外一幅呈120°辐射状排列,布局如图 1所示.天线单元为传统的半波偶极子,每幅天线的形式为相互独立馈电的交叉偶极子天线,偶极子交叉成90°,也就是天线阵一共包含8 个半波偶极子,可以方便地形成右圆极化和左圆极化模式.
|
图 1 昆明站MF雷达天线阵布局图 Fig. 1 The distribution of antenna array at Kunming station |
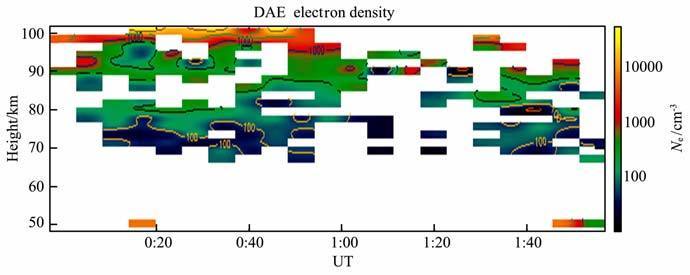
图 2是日食期间D 区电离层50~100km 之间电子密度的变化图,其中横坐标表示世界时,纵坐标表示高度.日偏食刚开始,太阳辐射通量开始减小,电子产生率也开始减小,但电子密度还没有明显变化,随着日偏食越来越大,电子密度开始逐渐减小,到08∶54LT,电子密度有一个明显减小,再到09∶11LT,日偏食达到最大,此时来自太阳的离化源,对于D 区来说主要是X 射线和Lyman-α射线大部分被月球遮挡,导致电子产生率达到最小,但电子密度此时并不会下降到最小,而是在09∶20LT 电子密度才达到最小值.从09∶42LT 开始电子密度逐渐恢复.从图 2可以发现在08∶54LT 与09∶45LT 之间的电子密度的有效观测值明显少于其他时刻,这可能与日食在D 区引起的某些物理过程有关,不过由于MF雷达的回波机制还没有定论,因此这里的原因也不能仅仅由电子密度的减小来解释,还有待于进一步的研究.
|
图 2 2009年7月22日日食期间电子密度随时间和高度变化图 Fig. 2 The image lines of electron density with the time and height during the Solar Eclipse on July 22,2009 |
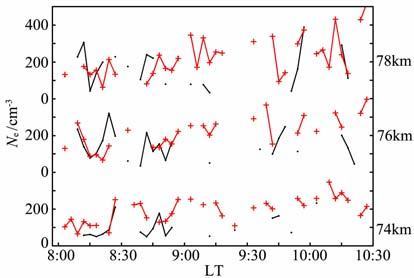
为了更加清楚地说明日食期间D 区电子密度的变化,图 3给出了74~78km 之间日食当天和日食前天的电子密度在同时间内的变化情况,黑“·"线表示日食当天的电子密度,红“+"表示日食前一天的电子密度.从图中可以清楚地看到日食期间的有效观测值比日食前一天同时间内的有效观测值少了许多.值得一提的是在日食当天的MF 雷达风场观测中观测到一个明显的重力波(这里没有给出),由于一些理论认为日食有可能在中高层大气中激发一种重力波,同时已有一些可能是由日食引起的重力波被观测到[24],另外Sugiyama曾经研究了中高层大气中重力波对电子密度的影响[25],所以该重力波是否由本次日食所激发以及该重力波对电子密度有何影响非常值得研究,该研究工作见于后面工作中.
|
图 3 日食当天和日食前天各个高度电子密度随时间的变化情况比较 黑“·"表示7月22日电子密度,红“+"表示7月21日电子密度. Fig. 3 The comparison of change in electron density withtime at eclipse time to that on the control day Black ‘ • ? denotes electron density on the 22 July, red ‘+Menotes electron density on the 21 July. |
为了克服日食期间雷达回波不足的问题,这里把74~78km 之间的观测结果叠加在一起作为这个区域的电子密度,又考虑到波动对于观测结果的影响,本文选择每个时刻的最大值作为有效电子密度,并对其进行二项式拟合,即
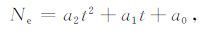
|
(9) |
其中:a0 =270.5;a1 =-14.07;a2 =0.25;t表示从上午8时开始雷达观测电子密度的次数.其拟合结果详见图 4.在图 4中,黑色圆点表示图 3中三个高度上电子密度的叠加,蓝线表示对每个时刻测得的电子密度的最大值的拟合,拟合曲线的最小值是Ne=72.54cm-3,取得最小值时t=28.拟合曲线较好地描述了日食期间D 区电子密度的变化特征.日食期间X 射线通量的变化直接影响电子产生率的变化,进而影响电子密度的变化.

|
图 4 图 3中各个高度电子密度的叠加及各个时刻最大电子密度的拟合 Fig. 4 The overlap of electron density at ditferent heights showed in the Fig.3 and the tit of the maximum electron density |
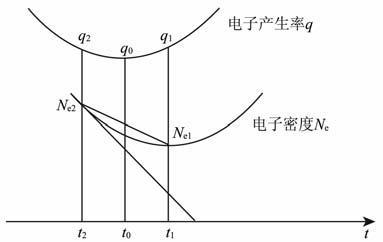
一般认为D 区的电子密度由光化平衡控制,D区的有效复合系数是一个非常重要的参数,在很大程度上决定了D 区的形态.但是复合系数的观测和测量通常是非常困难的[26],本文尝试利用日食期间MF雷达的观测数据估算D 区的有效复合系数,值得注意的是这里得到的只是日食期间的平均有效复合系数.在整个日食期间由于太阳辐射通量从初亏到食甚是逐渐减小,从食甚到复圆逐渐增大,而电子产生率直接受到太阳辐射的影响,所以假设日食期间的电子产生率是先减小后增大,在下面的模型中我们要假设电子产生率在先减小后增大过程中是对称分布的,在食甚时电子产生率最小,但是同时电子产生率还会受到太阳天顶角变化的影响,不过相对于日食效应其影响是可以忽略的.下面通过分析日食期间电子产生率和电子密度的变化关系,在不同假设条件下,建立模型估算有效复合系数.模型建立的理论框架简图见图 5.
|
图 5 日食期间电子产生率与电子密度变化特性的示意图 图中Ne1是电子密度剖面上最小一点,其对应的电子产生率与时间分别是q1 和t1;q2 是电子产生率剖面上与q1 对称相等点,其对应的电子密度和时间分别是Ne2和t2,t0 是电子产生率剖面上最小点q0 对应的时间. Fig. 5 The sketch map of the electron production rate (top),the electron density (bottom) and their relation Nel is the least point, corresponding electron production rate q1 and time tl,respectively;q2 is a point which is symmetry and equality with q1, corresponding electron density Ne2 and time t2 respectively,t0 is the time corresponding to the minimum of electron, q0. |
本模型主要利用了电子密度在食甚时不会达到最小值,而是存在一个后续时延才会达到最小值,同时假设日食期间电子产生率以食甚点对称分布.图 5为电子产生率曲线与最大电子密度拟合曲线的示意图.日食过程中假设有效复合系数不变.电子密度达到最小时刻t1 对应的电子密度值设为Ne1,相应时刻的电子产生率为q1,此外在电子产生率曲线图上假设t2 时刻有一q2 点与q1 点关于t0 时刻对称,且其值与q1 相等,q2 所对应的电子密度为Ne2,t0 是最小电子产生率q0 所对应的时间,于是存在如下关系:
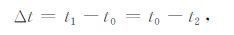
|
(10) |
当然,Ne1和Ne2都满足电子光化平衡:
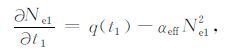
|
(11) |
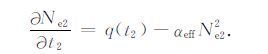
|
(12) |
因为Ne1点是电子密度的最小值,所以电子密度方程对时间的导数在Ne1 点的值等于零,即,在(t1,Ne1)点,
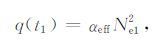
|
(13) |
又知q(t1)=q(t2),并把方程(13)代入方程(12)整理得:
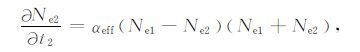
|
(14) |
再假设Ne2点的斜率近似等于Ne2和Ne1连线的斜率,并整理得到:
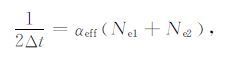
|
(15) |
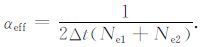
|
(16) |
本模式中用到的数据是采用日食期间74~78km的拟合结果,如图 4 所示,选用到的参数见表 3,将其代入式(16)得到:
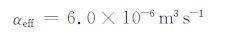
|
|
|
表 3 模式一的相关参数 Table 3 The parameter of the model 1 |
模型二主要是采用上面式(9)拟合得到的电子密度变化函数,利用光化平衡方程,并考虑到食甚点处电子产生率的时间导数为零的条件.
根据式(9)拟合得到的电子密度变化函数,显然电子密度Ne 应满足光化平衡方程(11)或(12).方程(11)两边对时间t求导数,并注意到在食甚时电子产生率q(t)为极小值,此时电子产生率对时间的导数等于零,因而得到:
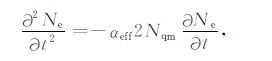
|
(17) |
其中Nqm是电子产生率最小时对应的电子密度,将t0 等于25(09∶11LT)代入式(9),得到Nqm=75cm-3.利用式(9)拟合得到的公式可以得到Ne 的一阶导数和二阶导数,代入方程(17)得到:
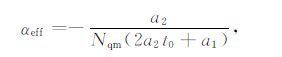
|
(18) |
将有关参数代入(18)式计算得到:
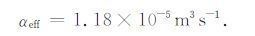
|
本文通过对日食期间的观测结果的分析,提出了两个模型来估算D 区的有效复合系数,两种模式分别在不同的假设条件下估算了有效复合系数,进而得到了电子产生率.两个模型的计算结果总结见表 4.
|
|
表 4 两个模型计算结果的比较 Table 4 Comparison of the results calculated by two models |
根据上述模型二的计算结果,把αeff = 1.18×10-5m3s-1,方程(9)及其对时间的一阶导数代入方程(11)得:
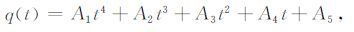
|
(19) |
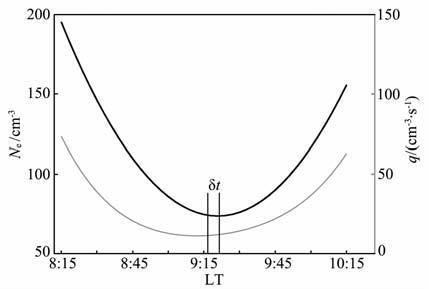
其中:A1 =αeffa22;A2 =2a2a1αeff;A3 =αeff(2a2a0+a12);A4 =2a0a1αeff+2a2;A5 =αeffa20+a1,q的单位是cm-3s-1.由此方程可以估算出电子产生率在日食期间的变化特征,具体计算结果见图 6.
|
图 6 日食期间电子产生率及电子密度关系图 Fig. 6 The relation between electron production rate and electron density |
不过,我们也注意到在利用日食期间观测到的电子密度,通过简单的模型计算有效复合系数的过程中,本文采用了一些假设条件,关于这些假设的可靠性及其对模型结果带来的影响程度,现分析总结如下:
(1) 在模型一中,我们需要准确判断电子密度达到最小的时间,而对于这个时间的测定可能存在较大的误差,因为在当前运行模式下MF 雷达的时间分辨率为3 min(通过改变运行模式,可以降低到1min),对于这次我们得到的9 min 的时延,这3min分辨率就可能给最后的复合系数带来大约33.3%的误差.另外,模型一中用Ne1和Ne2两点之间的连线代替了Ne2点的变化率,显然这将会使计算得到的复合系数偏小,而从结果上看模型一比模型二要小,有部分原因与此有关.
(2) 在模型二中,我们选用了74~78km 之间的电子密度中的最大值作为可信数据,并利用二项式拟合其变化特性,这个过程中可能存在一些风险.不过,这里我们一方面主要考虑到80km 以下电子密度的梯度还是比较小的[27],为了补充一个高度上观测数据的不足,才将这三个高度上的数据合并在一起;另一方面则与MF 雷达电子密度的测量原理有关,电子密度越小,则结果的可靠性越差,因而我们才选择每个时间点上的最大值作为日食期间的观测数据,而不是常用的平均值或中值.
(3) 模型一用了Ne1和Ne2两点拟合后的信息,并将两点连线代替了曲线在Ne2点的斜率,相比模型二只用了食甚点处拟合后的信息,模型一可能会对结果带来更大的误差,所以我们认为模型二更适合于中频雷达观测D 区有效复合系数的计算.
(4) 在两个模型中我们都假设了日食期间的电子产生率相对于食甚是对称的,因此这里得到的有效复合系数应该是平均值.同时实际上电子产生率在这段时间内还会受到太阳天顶角变化的影响[27],不过本文中在09∶03LT 和09∶20LT 时太阳天顶角分别为41°和37.6°,从而可以忽略太阳天顶角的影响[28].
整个日食期间,太阳辐射通量的变化直接影响电子产生率的变化,进而影响电子密度的变化.观测表明食甚时电子产生率达到最小,但是电子密度达到最低点的时刻与食甚并不同步,而是存在一个9min的时延,电子密度才减小至最小值.用二项式拟合的74~78km 之间各个时刻电子密度的最大值很好地描述了电子密度在日食期间的变化特征.
总之,本文基于上述分析只是尝试提出利用日食期间的MF雷达电子密度的观测结果来建立模型得到有效复合系数.两个模型计算出的有效复合系数都与以前的理论和观测[29, 30]保持了较好的一致性.
但是,电离层D 区包含丰富的离子成分,而不同离子的有效复合系数不同,有效复合系数主要受到离子成分分布的控制,另外温度也是一个重要的影响因素.这就决定了无论测定还是理论模拟D 区的有效复合系数都存在很大的困难,其方法的有效性和可靠性还有待更多观测数据的检验.
| [1] | 何友文, 孙宏林. 日食声重波效应. 电波科学学报 , 2001, 16(1): 93–99. He Y W, Sun H L. The acoustic-gravity wave effects of the solar eclipse. Chinese J. Radio Sci. (in Chinese) , 2001, 16(1): 93-99. |
| [2] | 刘立波, 万卫星, 涂剑南, 等. 一次日食电离层效应模拟研究. 地球物理学报 , 1999, 42(3): 296–303. Liu L B, Wan W X, Tu J N, et al. Modeling of the ionospheric effects during a total solar eclipse. Chinese J. Geophys (in Chinese) , 1999, 42(3): 296-303. |
| [3] | 何友文, 龙其利, 李永生, 等. 1987年9月23日日食电离层效应. 电波科学学报 , 1990, 5(1): 1–9. He Y W, Long Q L, Li Y S, et al. The ionospheric effects of the annular solar eclipse on 23 September 1987. Chinese J. Radio Sci. (in Chinese) , 1990, 5(1): 1-9. |
| [4] | 杨子杰, 石振华, 管荣生. 利用扫频后向散射法研究日环食的电离层效应. 电波科学学报 , 1990, 5(1): 10–17. Yang Z J, Shi Z H, Guan R S. A sweep-frequency backscatter study of the solar eclipse effects upon the ionosphere on September 23, 1987. Chinese J. Radio Sci. (in Chinese) , 1990, 5(1): 10-17. |
| [5] | 焦培南. 水平电子浓度梯度对Pmin(f)线的影响. 电波科学学报 , 1990, 5(1): 18–22. Jiao P N. The effect of the horizontal density gradient on Pmin(f)curve. Chinese J. Radio Sci. (in Chinese) , 1990, 5(1): 18-22. |
| [6] | 赵协中. 日食期间的甚低频传播效应. 电波科学学报 , 1990, 5(1): 23–31. Zhao X Z. The effect of VLF propagation during the solar eclipse. Chinese J. Radio Sci. (in Chinese) , 1990, 5(1): 23-31. |
| [7] | Huijun Le, Libo Liu, Xinan Yue, et al. The midlatitude F2 layer during solar eclipses: Observations and modeling. Journal of Geophysical Research , 2008, 113: A08309. DOI:10.1029/2007JAO013012 |
| [8] | Huijun Le, Libo Liu, Xinan Yue, et al. Latitudinal dependence of the ionospheric response to solar eclipses. Journal of Geophysical Research , 2009, 114: A07308. DOI:10.1029/2009JA014072 |
| [9] | Le H, Liu L, Yue X, et al. The ionospheric behavior in conjugate hemispheres during the 3 October 2005 solar eclipse. Ann. Geophys. , 2009, 27: 179-184. DOI:10.5194/angeo-27-179-2009 |
| [10] | Le H, Liu L, Yue X, et al. The ionospheric responses to the 11 August 1999 solar eclipse: observations and modeling. Ann. Geophys. , 2008, 26: 107-116. DOI:10.5194/angeo-26-107-2008 |
| [11] | 谢金来, 杨训仁, 李启泰. 日环食大气内重力波的探测和研究. 电波科学学报 , 1990, 5(1): 32–37. Xie J L, Yang X R, Li Q T. Detection and study of the atmospheric internal gravity waves on the annular solar eclipse. Chinese J. Radio Sci. (in Chinese) , 1990, 5(1): 32-37. |
| [12] | 潘炼德, 苗永瑞, 王发潮, 等. 日环食对低频及甚低频电波传播的影响. 电波科学学报 , 1990, 5(1): 38–43. Pan L D, Miao Y R, Wang F C, et al. The Influence of the annular solar eclipse on the propagation of the LF-VLF radio waves. Chinese J. Radio Sci. (in Chinese) , 1990, 5(1): 38-43. |
| [13] | 黄泽荣, 沈力, 李文涛. 中层大气的日食效应研究. 电波科学学报 , 1990, 5(1): 44–48. Huang Z R, Shen L, Li W T. Study of the middle atmospheric disturbance during the annular eclipse. Chinese J. Radio Sci. (in Chinese) , 1990, 5(1): 44-48. |
| [14] | 何建良, 张阿丽. 长波的日环食效应. 电波科学学报 , 1990, 5(1): 49–52. He J L, Zhang A L. The influence of annular solar eclipse on the LF propagation. Chinese J. Radio Sci. (in Chinese) , 1990, 5(1): 49-52. |
| [15] | 贾瑞进, 王凤霞, 赵益光. 日环食对近地大气传播特性的影响. 电波科学学报 , 1990, 5(1): 71–76. Jia R J, Wang F X, Zhao Y G. Effects of annular eclipse on the propagation in atmosphere close to the Earth. Chinese J. Radio Sci. (in Chinese) , 1990, 5(1): 71-76. |
| [16] | Holdsworth D A, Reid I M. The Buckland Park MF radar: routine observation scheme and velocity comparisons. Ann. Geophys. , 2004, 22: 3815-3828. DOI:10.5194/angeo-22-3815-2004 |
| [17] | Belrose J S, Burke M J. Study of the lower ionosphere using partial reflection 1. Experimental technique and method of analysis. Journal of Geophysical Research , 1964, 69(13): 2799-2818. DOI:10.1029/JZ069i013p02799 |
| [18] | Elmer H Hara. Approximations to the semiconductor integrals Cp(x) and Dp(x) for use with the generalized Appleton-Hartree magnetoionic formulas. Journal of Geophysical Research , 1963, 68(14): 4388-4389. DOI:10.1029/JZ068i014p04388 |
| [19] | Budden K G. The Propagation of Radio Waves. 1985 . |
| [20] | Gregory J B, Manson A H. Mesospheric electron number densities at 35 degree latitude. Journal of Geophysical Research , 1967, 72(3): 1073-1080. DOI:10.1029/JZ072i003p01073 |
| [21] | Robertson A G, Elford M, Cromption R, et al. Rotational and vibrational excitation of nitrogen by electron impact. Australian Journal of Physics , 1997, 50: 441-472. DOI:10.1071/P96092 |
| [22] | Phelps A V, Pack J L. Electron collision frequencies in nitrogen and in the lower ionosphere. Phys. Rev. Lett , 1959, 3: 340-342. DOI:10.1103/PhysRevLett.3.340 |
| [23] | Gregory J B, Manson A H. Seasonal variations of electron densities below 100 km at mid-latitudes—I Differential absorption measurements. Journal of Atmosphere and Terrestrial Physics , 1969, 31: 683-701. DOI:10.1016/0021-9169(69)90128-7 |
| [24] | Zerefos C S, Gerasopoulos E, Tsagouri I, et al. Evidence of gravity waves into the atmosphere during the March 2006 total solar eclipse. Atmos. Chem. Phys , 2007, 7: 4943-4951. DOI:10.5194/acp-7-4943-2007 |
| [25] | Sugiyama T. Response of electrons to a gravity wave in the upper mesosphere. Journal of Geophysical Research , 1988, 93(D9): 11083-11091. DOI:10.1029/JD093iD09p11083 |
| [26] | Whitten R C, Poppoff I G, Edmonds R S. Effective recombination coefficients in the lower ionosphere. Journal of Geophysical Research , 1965, 70(7): 1737-1742. DOI:10.1029/JZ070i007p01737 |
| [27] | Coyne T N R, Belrose J S. The diurnal and seasonal variation of electron densities in the midlatitude D region quiet conditions. Radio Science , 1972, 7: 163-174. DOI:10.1029/RS007i001p00163 |
| [28] | Rupa Vuthaluru. Mid-latitude D-region MF radar electron density observation . Adelaide University, 2003 |
| [29] | 张东和, 萧佐, 吴建, 等. 利用MF雷达对耀斑期间电离层D区电子密度的观测研究. 空间科学学报 , 2003, 23(5): 334–342. Zhang D H, Xiao Z, Wu J, et al. The study of the electron density in ionospheric D region using MF radar during flares period. Chin. J. Space Sci. (in Chinese) , 2003, 23(5): 334-342. |
| [30] | Osepian A, Kirkwood S, Dalin P, et al. D-region electron density and effective recombination coefficients during twilight-experimental data and modeling during solar proton events. Ann. Geophys. , 2009, 27: 3713-3724. DOI:10.5194/angeo-27-3713-2009 |
 2011, Vol. 54
2011, Vol. 54