海啸(tsunami)是生活在沿海地区的居民所面临的最严重的自然灾害之一,也是联合国“国际减灾十年"所确定的全球重大自然灾害之一[1].它的超强破坏力主要来自因强大作用力引起的水体的上升或下降所产生巨大势能转变为水体动能后的系列长波.海啸按产生源地的远近可分为越洋海啸(teletsunami)、区域海啸(regionaltsunami)和局地海啸(localtsunami)[2].
通过对海啸历史事件研究表明:破坏性海啸基本上都是越洋海啸[3],如1960年智利海啸、2004年苏门答腊海啸.那么,越洋海啸到底对我国有没有影响,有什么样的影响?至今未见学者给出定量的阐述.之前大部分专家学者基于对海啸历史事件资料的统计分析而得出了一些定性的研究成果---越洋海啸对我国沿海的影响不大或者基本无影响[4- 7],也有少数学者利用海啸数值模式对2004 年印度洋海啸以及1960 年智利海啸进行了数值模拟[3, 8, 9],但均未定量阐述此类海啸对我国各海区的影响.
本文认为:由于海啸事件、特别是灾害性海啸事件发生的频率很低,历史事件资料(海啸波高记录)和史书记载文献稀少,据其所得结论理论依据不够充分,就像在苏门答腊大海啸之前人们普遍认为印度洋的海啸危险性要比太平洋低,但印度洋海啸改变了人们对印度洋区域海啸危险性的认识.那么,越洋海啸对我国的危险性是否需要重新认识呢?本文将通过对2010年智利越洋海啸的数值模拟分析,试图定量阐述越洋海啸对我国沿海的影响,来回答上述疑问.
2 地震海啸数值模型地震海啸数值模型由两部分组成.一部分是计算海啸初始位移场的海啸源模型,也称断层模型;另一部分是基于线性或非线性浅水方程计算海啸波传播(propagation)和淹没(inundation)的海啸数值模型.
2.1 断层模型断层模型适用性是海啸波传播能否成功模拟的重要因素,它主要通过利用海床位移量来估算地震引起的初始水面高度.这样做的前提假定条件是:地震发生错动的过程是一个很短的冲击过程,可能发生在数秒内,水面变动与地震引起的断层错动同时发生;忽略了断层破裂的复杂性、错位的多向性、破裂层厚度可变性.
目前,国际上比较通用的是Mansinha & Smylie(1971)[10]以及Okada(1985)[11]基于弹性错移理论发展的两套断层模型;本文模拟中选取Smylie的理论模型进行海啸初始场的计算.
2.2 海啸传播数值模型地震海啸首波波长在量级相当于震源长轴尺度,通常可达几百千米,此时大洋水深和海啸波长的关系为:H/λ$\ll $1(H为特征水深,λ 为特征波长),因此海啸波将视为浅水长波,即海啸波在大洋中传播时不发生频散,传播速度为$\sqrt {gH} $,可达700km/h, 但波高却只有1 m 左右,甚至更小;加之海啸波在大洋中受到的摩擦力较小,所以越洋海啸可以在大洋中传播数千海里而能量衰减甚少,对数千海里外的沿岸地区也会造成海啸灾害[8, 9].当海啸波传播到近岸区域后由于水深急剧变浅,水体波动特性因受到地形影响而改变,主要表现为其传播方向、海啸高度以及剖面形状都要随之变化;特别当水深沿波向线逐渐变浅使得原先的海啸波波长急剧变短,波高骤增.
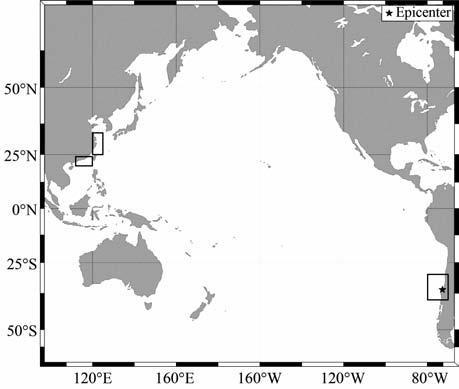
针对上述越洋海啸的传播特性,本文选取由美国华盛顿大学应用数学系DavidL George 研究开发的基于波浪追逐原理和自适应网格加密技术的海啸数值模型(GeoClaw)作为此次数值模拟的数学模型.此模型考虑了海啸波在近岸传播的非线性作用、底摩擦以及科氏力效应,并通过对海啸波高的追踪判断来确定是否进行加密计算,海啸波在大洋中的传播过程使用较粗网格分辨率进行计算,当海啸波到达近岸时模型会根据预先的参数设置自动加密到1′网格分辨率(图 1),这样就解决了高分辨率与计算效率之间的矛盾,大大提高了计算效率.
|
图 1 模型计算区域及地震震中位置(图中黑色五角星为震中位置,矩形框为近岸加密区域,分辨率为1′) Fig. 1 Range of studied area and location of epicenter (Black start and rectangle denote respectively the epicenter and refined region for 1 resolution) |
模型的控制方程采用如下守恒形式:
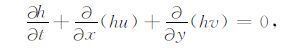
|
(1) |
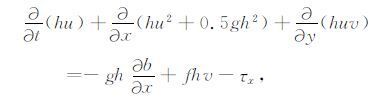
|
(2) |
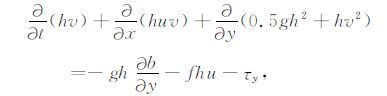
|
(3) |
式中,g为重力加速度常数;h为总水深;u、v分别为x,y方向的深度平均流速;t为时间;f为科氏力系数;b为海底表面水位;τx,τy分别表示x,y方向底摩擦项,可以表示为
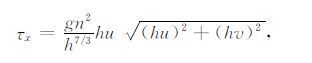
|
(4) |
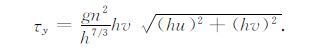
|
(5) |
其中n为曼宁系数.
模型采用二阶有限体积法计算非线性浅水方程.计算格式采用华盛顿大学RandallJ.LeVeque教授发展的一种波动追踪法,此方法是对经典Godunov方法的改进和拓展,我们知道Godunov方法是通过求解局部Riemann 问题精确解来得到全场全流场的数值解.它的致命缺陷是一阶精度,数值耗散太大;它求解局部Riemann 问题精确解,计算量非常大.RandallJ.LeVeque 教授发展的wave-propagation法的基本思路来源于Godunov 方法启发,同样属于间断分解法,但与Godunov通量差分法所不同的是,RandallJ.LeVeque基于波动物理量特征直接构造黎曼近似解,这样既提高了计算格式的精度,达到二阶精度.又大大提升了计算效率;对于非守恒双曲系统同样具有很好的适用性[12].
3 2010年智利地震海啸数值模拟2010年2月27日06时34分(北京时间27日14时34分),南美洲智利中南部近岸(36.1°S,72.8°W)发生8.8级地震,震源深度为35km.并引发了泛太平洋范围的海啸.
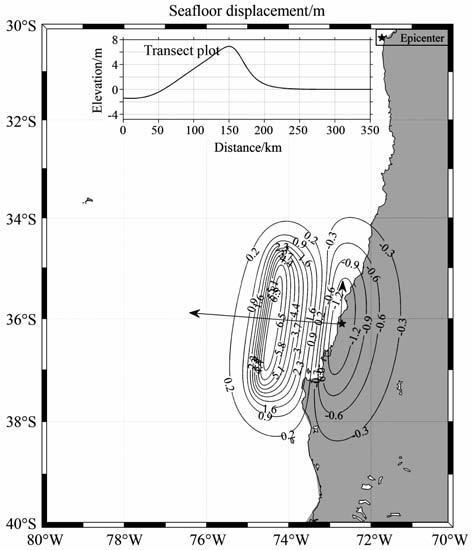
3.1 震源参数选取及海啸源计算如前所述,地震发生错动的过程是一个很短的冲击过程,因此可以假设海水表面的抬升与海底位移是“瞬间同步"完成的.将获得的震源断层参数(表 1)输入到断层模型即可获得地震海啸数值模型所需的初始场.其中断层长度(L)、断层宽度(W)、滑移量(D)根据文献[3, 8]中介绍的经验公式计算,断层倾角、滑移角、走向角来源于美国地质调查局(USGS)震源机制解.利用Mansinha & Smylie(1971)模型计算得到海啸初始场分布情况,计算结果见图 2.
|
|
表 1 2010年智利海啸的震源断层参数 Table 1 Fault parameters of 2010 Chile tsunami |
|
图 2 海啸初始位移(m)场和剖面曲线(图中黑色星代表震中位置) Fig. 2 Tsunami initial conditions and profile of seafloor displacement (m) (Black star denotes the epicenter) |
从断层模型计算的结果可知,最大海面抬升为+6.91m, 最大下沉位移量为-1.44m.由于地震地壳破裂的时间比海啸波的周期小1~2量级,因此假定主震发生的时刻即为海啸源的初始时刻,并用地壳破裂后的形状来估算海面的初始形状.用本节得到的初始场进行海啸的数值模拟是可信的.
3.2 海啸模拟本模拟所使用的地理信息数据均来源于ETOPO1数据库.计算区域为95°E~65°W,60°S~70°N(见图1).模型计算时大洋中采用5′网格分辨率计算,我国近海采用1′分辨率进行计算.波浪追踪加密判断标准为1cm.
本文模拟研究的重点区域为智利及智利周边区域沿海和中国近海的海啸波.
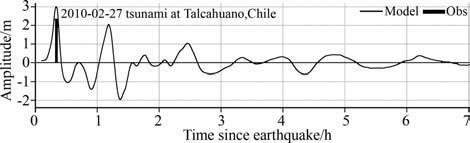
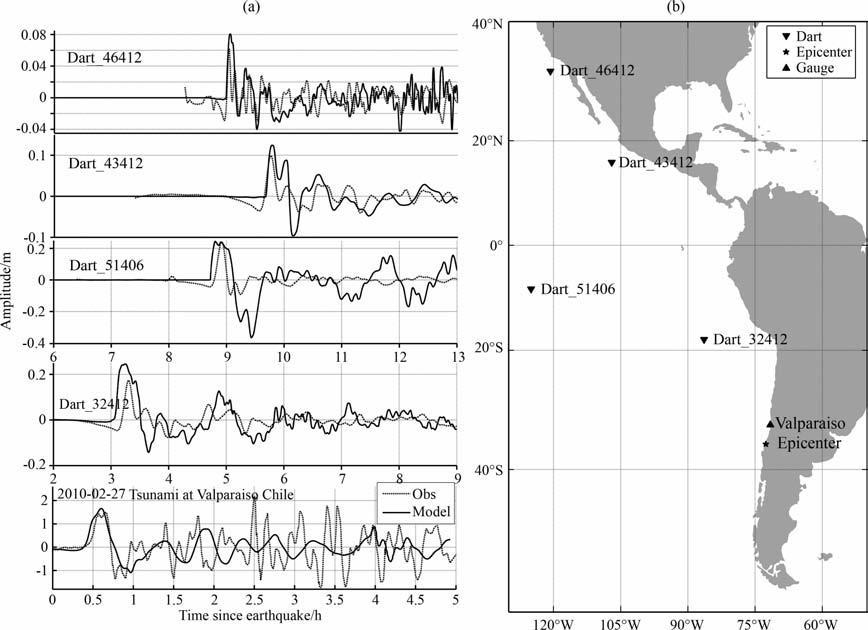
3.2.1 智利周边区域海啸波模拟地震发生20min后,观测资料显示地震海啸已经袭击了智利中部港口城市塔尔卡瓦诺(Talcahuano),海啸波高达2.34m, 图 3是数值计算得到的Talcahuano潮位站位置的海啸波高图和实测头波波幅以及到达时间(时间序列资料未能获得,这里只表现了先导波到达时间以及先导波振幅);从对比的结果(图 3)可以看出模式计算得到的海啸先导波无论从位相还是波幅都与实际数据相吻合.随后智利瓦尔帕莱索(VALPARAISO)验潮站、32412海啸浮标和美国的51406、46412、43412海啸浮标也先后监测到约0.06~1.4m的海啸波,图 4 为我们计算得到的43412、46412、51406、32412以及Valparaiso五个位置的海啸波与实测海啸波对比情况,模拟结果成功再现了海啸波在上述五个位置的传播序列,拟合效果良好.
|
图 3 Talcahuano站模拟结果(实线)与验潮站实测海啸头波记录对比 Fig. 3 Comparision between numerical simulation results(solid) and tidal gage measurements ( bar) for leading-wave at Talcahuano |
|
图 4 海啸浮标站46412、43412、51406、32412以及Valparaiso验潮站各站点模拟结果与实测数据对比(a)及各站点位置分布(b) Fig. 4 Comparison between numeric, ^ simulation results (solid) and tide gages measurements (dash dot) at select sites and the k)cation map |
|
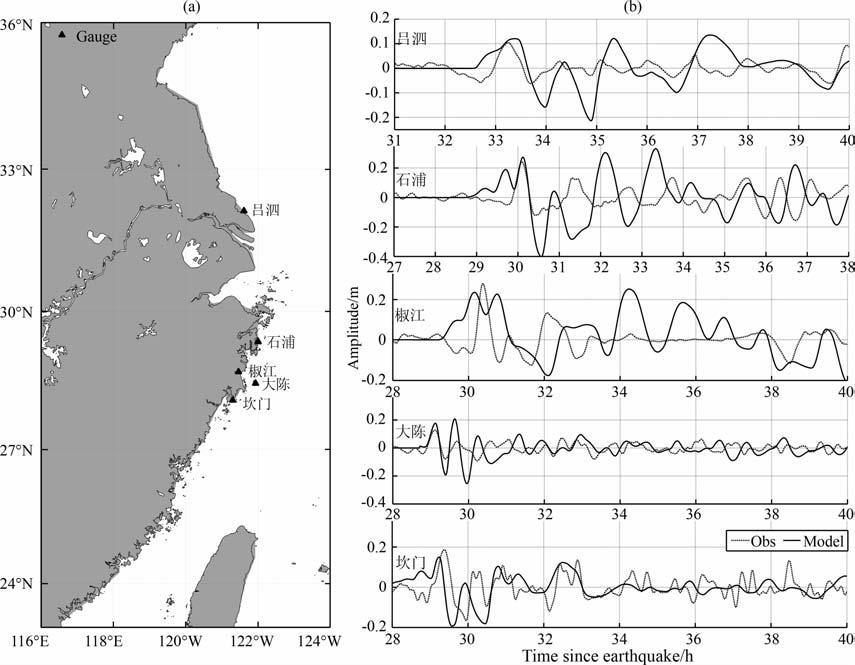
图 5 所选站点位置分布(a)以及模拟结果与实测数据对比(b) Fig. 5 丁he location map(a)and comparison between numerical simulation results(solid) and tidal gauge measurements(dash dot) at select sites(b) |
|
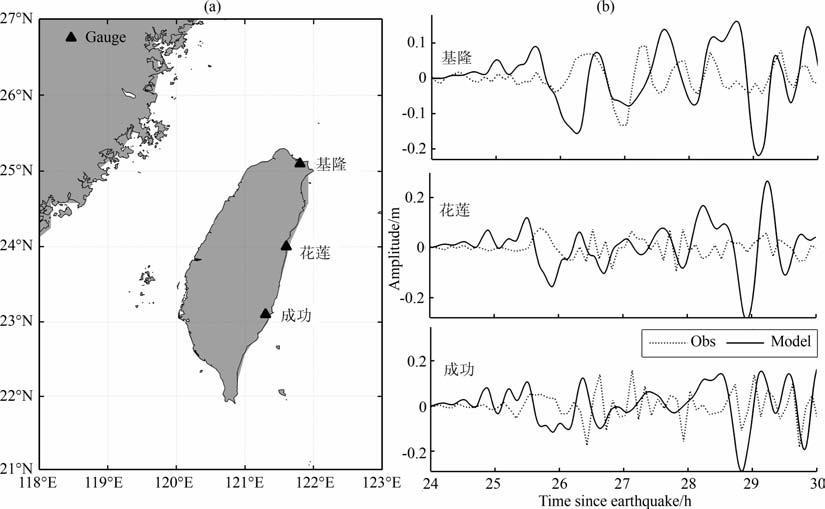
图 6 台湾地区所选站点位置分布(a)以及模拟结果与实测数据对比(b) Fig. 6 The location map(a^^for Taiwan region gauges and comparison between numericalsimulation results (solid) and tide gauge measurements (dash dot) at select sites (b) |
|
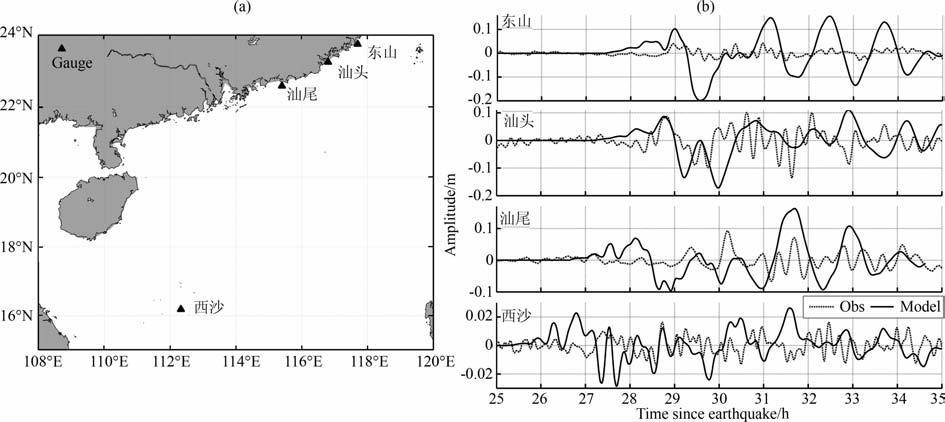
图 7 (a)南海区域所选站点位置分布;(b)南海区域所选站点模拟结果与实测数据对比 Fig. 7 (a) Distribution of the selected site location in South China Sea; (b)Comparison between numericalsimulation results (solid) and tide gauge measurements (dash dot) at select sites in South China Sea |
从上述21个所选验潮站和浮标点的模拟情况可以看出,无论是海啸浮标还是验潮站,海啸数值模式对海啸波的模拟与实测海啸波基本一致.其中,对海啸浮标点处的海啸波模拟程度最好,模拟与实测整个曲线几乎一致.而沿海海洋站的海啸波,模拟海啸波先导波的符合程度很好,后续波动则有一定差距.
海啸浮标的海啸波模拟结果很好而验潮站的后续海啸波模拟结果稍差的原因是:(1)海啸浮标都分布于深水大洋区,海啸波受地形影响非常小;而验潮站基本都分布于沿海浅水区,局地地形对于海啸波的影响非常大;(2)模型所选水深和地形数据的空间分辨率不高,近岸与实际地形存在较大偏差,导致模型无法真实刻画微地形对海啸波传播过程的影响.
另外,海啸源模型精度存在偏差等原因对模拟结果也有一定的影响.
4 智利海啸对我国沿海的影响分析以往研究表明:我国沿海特别是东海、南海以及台湾岛地区面临琉球海沟和马尼拉海沟潜在地震海啸(局地海啸)的威胁[13, 14],是地震海啸的高风险区.那么,越洋海啸对中国的影响又将如何?国内学者普遍认为越洋海啸对中国大陆沿海造成破坏的可能性很小[4, 5, 8].主要原因是我国海区浅水大陆架宽广,外围自北向南有:千岛群岛、日本群岛、琉球群岛、菲律宾群岛、印尼诸岛的环绕,形成一道天然屏障,越洋海啸进入这一区域后,海啸波能量迅速衰减不利于海啸波的传播.本文基于数值模拟方法,就越洋海啸传播特征、最大波高分布阐述产生于南美洲中部的越洋海啸对中国沿海的影响.
海啸波于24h 后抵达日本本州岛和北海道东部沿海,波高大多为20~80cm.其中岩手县久慈港和宫城县仙台港先后观测到1.2 m 和1.1 m 的海啸波高.大约25h到达我国沿海,25h 对于海啸的预警是完全可能的.虽然此次海啸事件未对我国造成灾害性影响,但这不等于此类海啸均不会对我国沿海造成威胁,更不能毫无预防.
从最大海啸波高分布图(图 8)来看,此次海啸横扫了整个太平洋,东南太平洋、特别是智利及其周边区域是此次海啸能量的主要分布区,在彼岸的西北太平洋区域国家中中国、日本、俄罗斯都受到影响.对我国大陆沿海的影响主要分布在广东珠江口(图 9)、江苏南部到福建闽江口(图 10)及台湾岛东部一带沿岸.
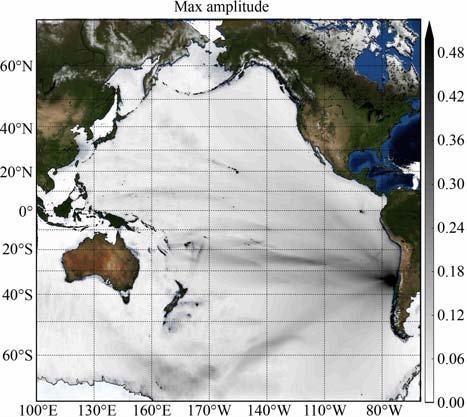
|
图 8 最大海啸波高分布(单位:m) Fig. 8 Maximum tsunami height distribution(Unit:m) |
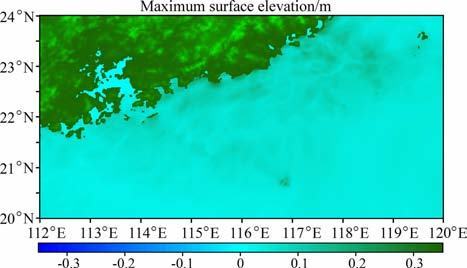
|
图 9 珠江口区域最大海啸波高分布(单位:m) Fig. 9 Maximum tsunami height distribution aroundPearl River estuary region(Unit:m) |
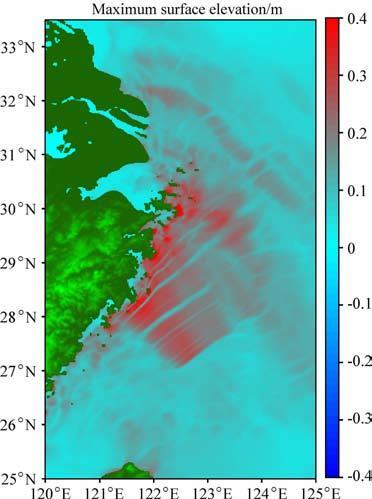
|
图 10 长江口、杭州湾区域最大海啸波高分布(单位:m) Fig. 10 Maximum tsunami height distribution around Yangtze River estuary and Hangzhou Bay region(Unit : m) |
目前,我们能够看到的只有沿海为数不多几个海洋站的监测数据,海啸波最高水位为28cm.为了研究海啸波对我国沿海的影响,主要是考虑海啸波到达我国沿海近岸(拟取距岸1 m 等深线)时的高度,本文选取了沿海420个点输出海啸波幅.但由于所采用水深地形数据精度所限,本文数值模型计算得到的最精确的海啸波幅是距岸10m 等深线处海啸波幅.因此利用格林定律由水深10 m 等深线处的海啸波幅来推算近岸海啸波幅.
根据格林定律[15]:我们可以得到b0d01/2 h02 =b1d11/2 h12,其中d是水的深度,b是海啸波射线间的距离,h是海啸振幅,下标0和1表示两个不同的地点.如果在0处(如在源区)的海啸振幅已知,则海啸传播到1处的振幅为:
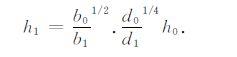
|
式中b0/b1 表示射线的发散程度.
本文首先确定距离沿岸420 个输出点较近的10m 等深线上同样个数的点作为模型计算点,然后由数值模型输出420 个计算点的海啸波幅,最后根据格林定律推算近岸处420 个输出点的海啸波幅.这样我们可以得到智利海啸在中国沿岸1 m 等深线处(除渤海、黄海北部外)最大波高分布情况(图11).虽然海洋站实测最高海啸波幅为28cm, 但从图中可以看到此次海啸最大海啸波高分布在杭州湾南部和台湾东北部沿岸,可达到80cm.
由古登堡-里克特断层辐射能量测算公式[16]和能量与波高近似转换关系可知,如果此次地震的震级为1960年的Mw=9.5 级,那么长江口以南至浙江温州一带以及台湾东部地区近岸最大海啸波幅将达到220cm 以上;这样规模的波幅如果恰逢当地高潮位必将在当地造成严重的海啸灾害,给当地沿岸居民的生命财产造成巨大损失,即使未能叠加到高潮位,如此规模的海啸波幅也将对近岸港口码头、近海海洋工程造成严重威胁,特别容易引起港湾的共振,形成假潮现象.
5 结论2010年2 月27 日在智利中南部发生了Mw=8.8级地震,并引发了泛太平洋区域的海啸,事件发生后太平洋沿岸多个国家的验潮站和海啸监测系统都捕捉到了此次海啸,其中仪器监测到的最大海啸波出现在智利的塔尔卡瓦诺,波高达2.34m(时间:2010年2月27 日06 时53 分,世界时).海啸波大约25h后到达我国近海,我国近海海洋观测系统监测到5~28cm 的海啸波幅.
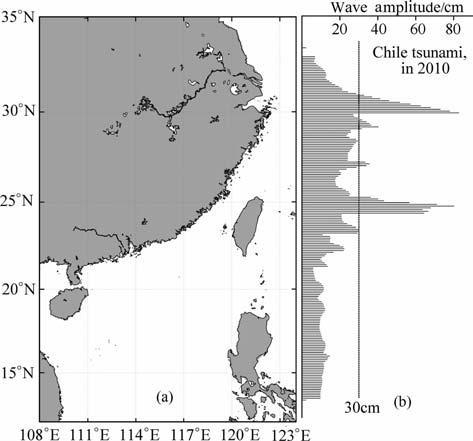
|
图 11 2010年智利海啸在中国沿岸最大波幅分布 Fig. 11 Area distribution of maximum wave amplitude along coastline of China for Chile tsunami in 2010 |
利用海啸数值模型重点模拟了此次海啸在我国沿海及智利周边区域的传播特征,模拟结果与实测数据吻合良好;通过对数值结果的分析,得出此次海啸对我国沿海的影响主要分布在长江口至福建闽江口、台湾东部以及珠江口区域,其中长江口以南至浙江温州一带以及台湾东部地区最大海啸波幅可达到80cm.虽然此次海啸未对我国沿海造成灾害,但通过古登堡-里克特地震断层辐射能量测算公式和能量与波高近似转换关系可知,如果此次地震的震级为1960年的Mw=9.5,那么长江口以南至浙江温州一带以及台湾东部地区最大海啸波幅将达到220cm以上.那么,以往研究普遍认为的越洋海啸对我国大陆沿海造成破坏性的可能性很小的观点是值得重新商榷的.本文认为太平洋区域的越洋海啸,特别是Mw≥9级以上的越洋海啸对我国沿海同样具有造成破坏性的威胁.因此今后有必要重视和加强越洋海啸预警报技术研究、建立健全海啸监测及预警系统、开展海啸灾害风险区划评估工作,以防范未来潜在的海啸风险.
致谢感谢两位评审专家对本文提出的宝贵意见.
| [1] | 于福江, 叶琳, 王喜年. 1994年发生在台湾海峡的一次地震海啸的数值模拟. 海洋学报 , 2001, 23(6): 32–39. Yu F J, Ye L, Wang X N. The simulation of tsunami happened in the Taiwan Strait in 1994. Acta Oceanologica Sinica (in Chinese) (in Chinese) , 2001, 23(6): 32-39. |
| [2] | UNESCO-IOC. Tsunami Glossary. IOC information document O.1221. Paris, UNESCO, 2006 http://www.oalib.com/references/18895548 |
| [3] | 温瑞智, 任叶飞, 周正华, 等. 越洋海啸的数值模拟. 地震工程与工程振动 , 2008, 28(4): 28–34. Wen R Z, Ren Y F, Zhou Z H, et al. Preliminary study on numerical simulation of transoceanic tsunami. Journal of Earthquake Engineering and Engineering Vibration (in Chinese) (in Chinese) , 2008, 28(4): 28-34. |
| [4] | 包澄澜. 海啸灾害及其预警系统. 国际地震动态 , 2005, 313(1): 14–18. Bao C L. Tsunami disaster and its re-warning system. Recent Development in World Seismology (in Chinese) (in Chinese) , 2005, 313(1): 14-18. |
| [5] | 包澄澜, 叶琳. 海啸灾害与预警. 海洋预报 , 2005, 22(1): 1–4. Bao C L, Ye L. Tsunami disaster and it's warning. Marine Forecasts (in Chinese) (in Chinese) , 2005, 22(1): 1-4. |
| [6] | 郭增建, 陈鑫连. 地震对策. 北京: 地震出版社, 1986 . Guo Z J, Chen X L. Earthquake Countermeasure (in Chinese). Beijing: Seismological Press, 1986 . |
| [7] | 王晓青, 吕金霞, 丁香. 我国地震海啸危险性初步探讨. 华南地震 , 2006, 26(1): 76–80. Wang X Q, Lü J X, Ding X. A preliminary study on the risk of tsunami in China. South China Journal of Seismology (in Chinese) (in Chinese) , 2006, 26(1): 76-80. |
| [8] | 任叶飞.基于数值模拟的我国地震海啸危险性分析研究.哈尔滨:中国地震局工程力学研究所,2007. Ren Y F. Study on China earthquake tsunami hazard analysis based on numerical simulation (in Chinese). Harbin: Institute of Engineering Mechanics, China Earthquake Administration, 2007 http://www.oalib.com/references/18895551 |
| [9] | 付庆军.越洋和局地海啸数值模拟的理论研究及其应用.天津:天津大学, 2006. Fu Q J.Research on theory and application of trans-oceanic tsunami and local tsunami numerical simulation (in Chinese). TianJin: TianJin University, 2006 http://cdmd.cnki.com.cn/Article/CDMD-10056-2008184406.htm |
| [10] | Mansinha L, Smylie D E. The displacement fields of inclined faults. Bulletin of the Seismological Society of America , 1971, 61(5): 1433-1440. |
| [11] | Okada Y. Surface deformation due to shear and tensile faults in a half-space. Bulletin of the Seismological Society of America , 1985, 75(4): 113-1154. |
| [12] | Leveque R J. Wave propagation algorithms for multi-dimensional hyperbolic systems. Journal of Computational Physics , 1997, 131: 327-335. DOI:10.1006/jcph.1996.5603 |
| [13] | 叶琳, 王喜年, 包澄澜. 中国的地震海啸及其预警服务. 自然灾害学报 , 1994, 3(1): 100–103. Ye L, Wang X N, Bao C L. Tsunami in the China Seas and its warning service. Journal of Natural Disasters (in Chinese) (in Chinese) , 1994, 3(1): 100-103. |
| [14] | 郭彩玲, 王晓峰. 中国东部海域发生海啸的可能性分析. 自然灾害学报 , 2007, 16(1): 7–11. Guo C L, Wang X F. Possibility analysis of tsunami taking place in east sea area of China. Journal of Natural Disasters (in Chinese) (in Chinese) , 2007, 16(1): 7-11. |
| [15] | Satake K. 海啸.世界地震译丛. 薛艳译,2006,3:59-75 Satake K. Tsunamis.Translated by Xue Y. Translated World Seismology(in Chinese), 2006,3:59-75 |
| [16] | Peter M Shearer著.地震学引论. 陈章立译. 北京:地震出版社,2008 Peter M Shearer. Introduction to Seismology (in Chinese). Chen Z L translated. Beijing: Seismological Press,1998 |
 2011, Vol. 54
2011, Vol. 54



