自相关法单频干扰识别与消除方法

引用本文

高少武, 赵波, 祝树云等. 自相关法单频干扰识别与消除方法. 地球物理学报, 2011, 54(3): 854-861, doi: 10.3969/j.issn.0001-5733.2011.03.026. 复制到剪切板

GAO S W, ZHAO B, ZHU S Y, et al. Identification and elimination of monofrequency interference in seismic data by an autocorrelation algorithm. Chinese J. Geophys. (in Chinese), 2011, 54(3): 854-861, doi: 10.3969/j.issn.0001-5733.2011.03.026. 复制到剪切板

自相关法单频干扰识别与消除方法

高少武^1,2 , 赵波² , 祝树云² , 罗国安² , 贺振华¹

1. 成都理工大学油气藏地质与开发工程国家重点实验室,成都 610059;
2. 中国石油集团东方地球物理公司物探技术研究中心,涿州 072750

收稿日期 2010-03-12, 2011-01-11 收修定稿

基金项目: 国家重大专项(2008ZX05019-004,2008ZX05019-003)资助.

作者简介: 高少武,男,1965年生,高级工程师,博士. 现主要从事物探处理方法研究与软件开发工作. E-mailgaoshaowu@cnpc.com.cn

摘要: 常规单频干扰压制方法需要估算频率、振幅和相位,由于频率和相位与单频干扰呈非线性函数关系,因此任何参数估算方法都会非常费时,且计算效率低下. 本文提出的自相关法单频干扰识别与消除方法,利用地震数据自相关函数计算单频干扰自相关函数,采用余弦函数自适应减算法快速估算单频干扰. 本方法不需要估算单频干扰的频率、相位和振幅参数,因此可以高效快速地估算出单频干扰并予以消除. 本方法最突出优点是能够快速有效地消除单频干扰,且不伤害干扰附近的有效信号,提高了单频干扰频率分量附近数据的信噪比. 合成数据和实际数据试算结果表明该方法是有效和可行的.

关键词: 地震数据采集单频干扰信噪比自适应减算法自相关法

Identification and elimination of monofrequency interference in seismic data by an autocorrelation algorithm

GAO Shao-Wu^1,2, ZHAO Bo², ZHU Shu-Yun², LUO Guo-An², HE Zhen-Hua¹

1. State Key Laboratory of Oil and Gas Reservoir Geology and Exploitation, Chengdu University of Technology, Chengdu 610059, China;
2. Geophysical Technique Research Center, BGP, CNPC, Zhuozhou 072750, China

Abstract: Traditional monofrequency interference (MFI) suppression methods need to estimate the frequency, phase and amplitude of the MFI. However, a MFI has a nonlinear relationship with the frequency and phase parameters, and any parameter estimation is time consuming, its computational efficiency is very low. In the autocorrelation algorithm (ACA) proposed in this paper, the autocorrelation function of the MFI is computed by seismic records. Following that, the MFI is quickly estimated by a cosine function adaptive subtraction algorithm. The proposed method need not estimate the frequency, phase and amplitude of the MFI, so the MFI can be high-efficiently estimated and eliminated. The most prominent advantage of the ACA is that only interference with MFI component can be quickly and effectively eliminated, and useful signals have not been harmed. Therefore, the signal-to-noise ratio is improved in the vicinity of a MFI frequency component. The synthetic and real data examples illustrate that the proposed method is feasible and effective..

Key words: Seismic data acquisition Monofrequency interference Signal-to-noise ratio Cosine function adaptive subtraction algorithm Autocorrelation algorithm

1 引言

随着地震勘探的出现，就伴随着单频干扰的识别与压制问题.在20 世纪80 年代以前，由于地震数据处理技术和设备的限制，只能完全依靠野外地震数据采集过程中，通过地震仪器设计的陷波器，来压制地震数据中的单频干扰^[1~5].单频干扰识别和压制效果很不理想.

随着数字信号处理技术和计算机技术的发展，室内单频干扰处理技术也开始起步.室内处理第一阶段是频率域压制法和陷频滤波法.郭其贵^[6]提出了利用相位滤波原理，设计一个50Hz的陷波器，压制地震数据中的单频干扰.凌云等^[7]提出了在频率域利用中值滤波压制单频干扰的方法.这两种方法虽然处理简单､快捷，且对单频干扰有一定的压制效果，但在处理后的地震数据中还残留很强的剩余单频干扰，同时对单频频率附近有效信号频率成分造成严重伤害.单频干扰压制效果并不理想，不能满足高分辨率高信噪比地震数据单频干扰消除与压制处理的需要.

室内单频干扰处理更多地采用函数逼近方法估算单频.包括余弦函数逼近法和正余弦函数逼近法.余弦函数逼近法就是把单频干扰表示为振幅､频率和相位(时延)的余弦函数，通过估算这三个参数达到压制单频干扰.正余弦函数逼近法就是把单频干扰表示为相同频率､不同振幅的余弦函数和正弦函数的组合，通过估算正弦函数振幅､余弦函数振幅和频率三个参数达到压制单频干扰.对于单频干扰，有许多消除方法^[8~18].这些方法都是通过估算单频频率(和时延)以达到估算单频干扰的目的.由于单频频率(和时延)与单频干扰呈非线性函数关系，因此估算非常费时.随着高覆盖､高密度地震采集技术的推广应用，迫切需要更加高效的计算方法.

自相关运算是地震勘探数据处理领域最常用的运算^[19~21].因为正余弦函数的自相关运算结果仍是同频率的正余弦函数，那么单频干扰的自相关运算结果仍是同频率的正余弦函数.因此，可以通过自相关运算来确定单频干扰.本文提出了自相关法单频干扰识别与消除方法以消除地震数据中的单频干扰.通过地震数据自相关运算，计算确定单频干扰余弦函数，采用余弦函数自适应减算法快速估算单频干扰.该方法并不需要估算单频干扰频率､相位和振幅参数，而是直接估算单频干扰.该方法不损害有效信号，能够有效提高单频干扰频率分量附近数据的信噪比.

2 方法原理

地震记录可以表示为地震有效信号与单频干扰的和，即

(1)

式中，x(t)表示地震记录；S(t)表示地震有效信号；y(t)表示单频干扰；t表示时间.

2.1 地震数据自相关分析

地震数据自相关定义为

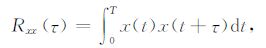
(2)

将方程(1)代入(2)，有

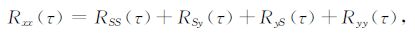
(3)

其中，R_xx(τ)表示地震记录的自相关；R_SS(τ)表示地震有效信号的自相关；R_Sy(τ)表示地震有效信号与单频干扰的互相关；R_yS(τ)表示单频干扰与地震有效信号的互相关；R_yy(τ)表示单频干扰的自相关.

假设地震数据与单频干扰是不相关的，则它们之间的互相关为零，即

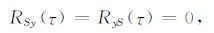
(4)

将方程(4)代入(3)，有

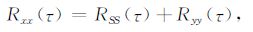
(5)

即，一个地震记录之间的自相关就是地震有效信号之间的自相关与单频干扰之间的自相关之和.从方程(5)可以看出，如果地震有效信号之间的自相关为零，则单频干扰之间的自相关就是地震记录之间的自相关.即

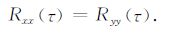
(6)

由于在地震数据深层，地震有效信号能量与单频干扰能量相比，要小得多，因此利用深层资料估算地震数据之间的自相关，方程(6)会近似满足.对于地震数据初至到达时间之前，由于还没有地震有效信号到达，方程(6)理论上完全满足.因此为了估算单频干扰之间的自相关，可以使用地震数据初至到达时间之前的数据来估算，如果初至时间比较小，则可以使用深层地震数据来估算.

2.2 单频干扰自相关分析

余弦函数单频干扰逼近表达式是^[8]

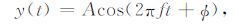
(7)

式中，A表示单频干扰的振幅，f表示单频干扰的频率，Φ 表示单频干扰的相位，t表示单频干扰的时间.

将方程(7)代入方程(2)中，且假定T是单频干扰周期或周期整数倍，经过简单运算，有

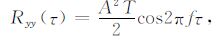
(8)

在方程(8)中，令τ=0，则有

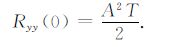
(9)

将方程(9)代入方程(8)，并把τ 换成t，有

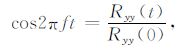
(10)

将方程(6)代入方程(10)中，有

(11)

方程(11)就是利用地震数据自相关函数计算单频干扰余弦函数的计算公式.对给定的地震数据，仅仅需要计算一次自相关，就可以确定单频干扰的余弦函数.显然运算次数要远远小于各种单频干扰估算运算次数.对于几十万甚至几千万道的叠前3D 地震数据来说，运算效率是相当可观的.

2.3 余弦函数自适应减算法

由方程(11)估算出单频干扰余弦函数之后，采用基于余弦函数自适应减算法估算单频干扰，可以省去估算单频干扰频率､振幅和相位三个参数.基于余弦函数自适应减单频干扰向量可以表示为

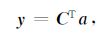
(12)

式中，y表示单频干扰向量；C表示单频干扰余弦函数矩阵；a表示单频干扰余弦函数系数向量.且

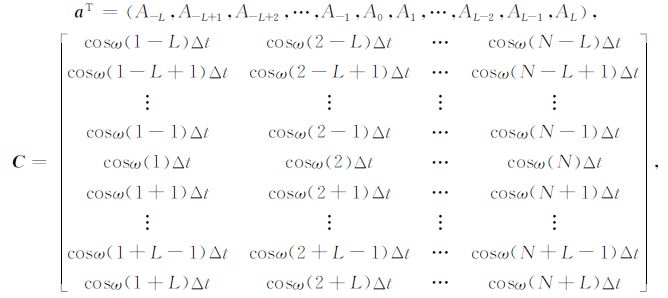
(13)

式中，Δt表示时间采样间隔，N表示地震记录长度，(2L+1)表示单频干扰余弦函数系数个数.

由最小二乘方法，确定出单频干扰余弦函数系数向量a的计算公式

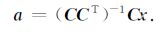
(14)

这样已知地震数据，由方程(2)计算自相关函数，由方程(11)计算单频干扰余弦函数，由方程(13)构造余弦函数矩阵C，由方程(14)可以求解出单频干扰余弦函数系数向量a，由方程(12)可以计算单频干扰向量y.从地震数据中减去单频干扰，以达到消除单频干扰目的.

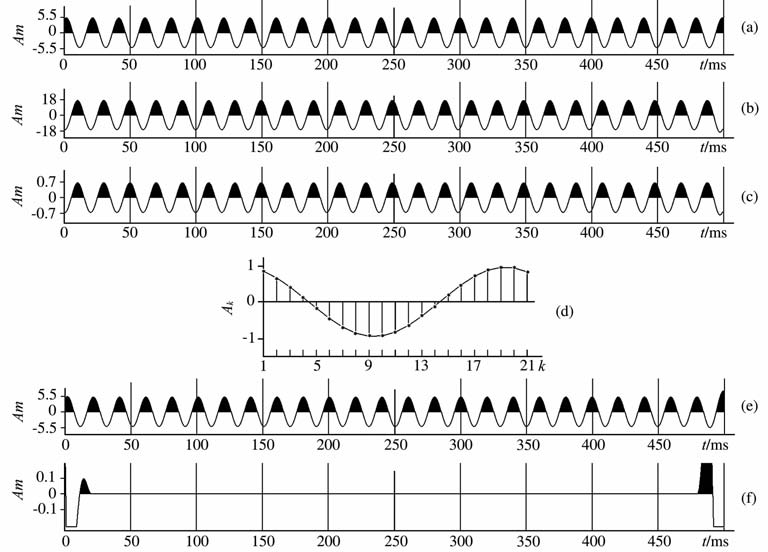
3 合成数据例子

首先使用合成数据例子来说明自相关法的可行性和有效性.图 1是自相关法理论单频数据计算和对比.理论单频数据采用文献[13]中方程(1)的生成.这里使用的参数是:单频余弦函数和正弦函数的振幅分别是2.543和4.816；单频频率是50.135Hz；时间采样间隔Δt是1ms, 样本个数N是500，计算的理论数据如图 1a所示.图 1b 是由方程(2)计算的自相关函数，其中T取值为80 ms, 图 1c是由方程(11)计算的单频余弦函数.对于L=10，由方程(14)计算的单频振幅向量如图 1d所示.图 1e是由方程(12)计算的单频.且计算了图 1a理论单频数据与图 1e计算单频之间的互相关，其互相关值为0.9988，即理论单频数据与计算单频数据之间完全一致.图 1f是图 1a理论单频数据与图 1e计算单频之差，从图中可以看出，仅仅在数据的起始20ms和终止20ms部分，计算的边界效应产生数据之间的误差外，数据中间部分的误差很小，几乎为零.因此表明自相关法在理论上是有效的.

图 1 自相关法合成数据计算和对比 (a)理论单频数据；(b)自相关函数；(c)单频余弦函数；(d)单频振幅向量；(e)计算单频；(f)计算单频与理论单频误差. Fig. 1 Computation and comparison of the ACA for a synthetic data (a) Synthetic MF； (b) Autocorrelation function； (c) MF cosine function； (d) MF amplitude vector； (e) Computed MF；(f) Error between the computed and the synthetic MF.

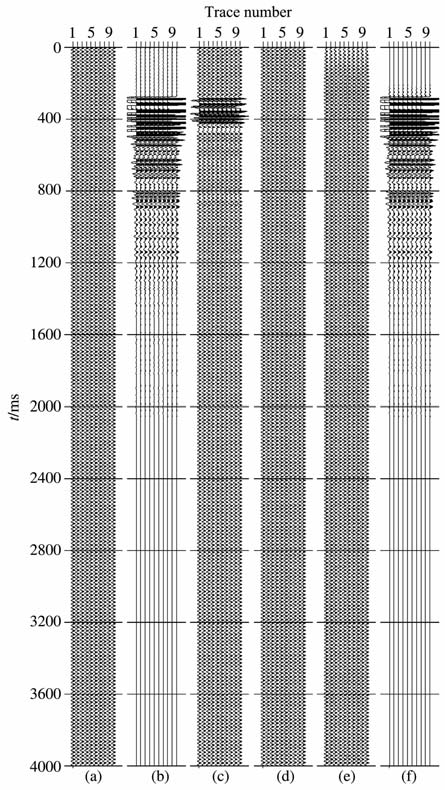
图 2是自相关法合成数据对比.理论单频数据仍采用文献[13]中方程(1)的生成，这里使用的参数是:单频余弦函数和正弦函数的振幅分别是7.541和4.811；单频频率是50.254Hz；时间采样间隔Δt是1ms, 样本个数N是4000，生成单频干扰数据，每一道的数据10道显示如图 2a所示.信号采用一段实际地震数据，其最大值为单频5倍，如图 2b所示，生成的理论数据如图 2c所示，通过自相关法计算出的单频干扰余弦函数如图 2d所示，计算生成的单频干扰数据如图 2e所示，自相关法处理后恢复的信号如图 2f所示.

图 2 自相关法合成数据效果对比 (a)合成干扰；(b)实际信号；(c)合成数据；(d)计算余弦函数；(e)计算干扰；(f)恢复信号. Fig. 2 Result comparison of theACA for a synthetic data (a) Synthetic MF； (b) Real signal； (c) Synthetic data； (d) Computed cosine function； (e) Computed MFI； (f) Recovered signal.

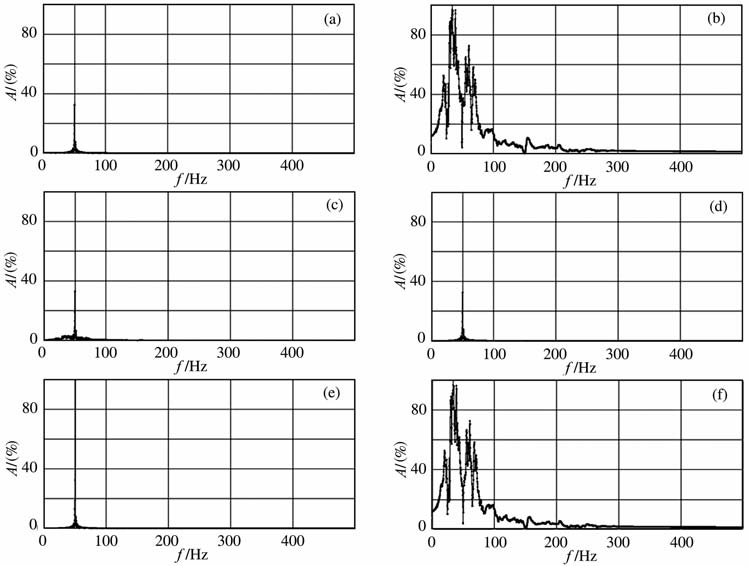
图 3是自相关法合成数据频谱对比.从数据和频谱显示上看，自相关法有效地识别并消除了单频干扰，且没有伤害单频干扰频率附近信号的频率成分，因此有效地提高了单频干扰附近信号的信噪比.

图 3 自相关法合成数据频谱效果对比 (a) 合成干扰; (b) 实际信号; (c) 合成数据; (d) 计算余弦函数; (e) 计算干扰; (f) 恢复信号. 它们的最大振幅值分别是13678683、3673464、12983530、13679288、13658404和3661707. Fig. 3 Result spectrum comparison of the ACA for a synthetic data (a) Synthetic MF; (b) Real signal; (c) Synthetic data; (d) Computed cosine function; (e) Computed MFI; (f) Recovered signal. Their maximum amplitude values are 13678683, 3673464, 12983530, 13679288, 13658404 and 3661707, respectively.

4 实际数据例子

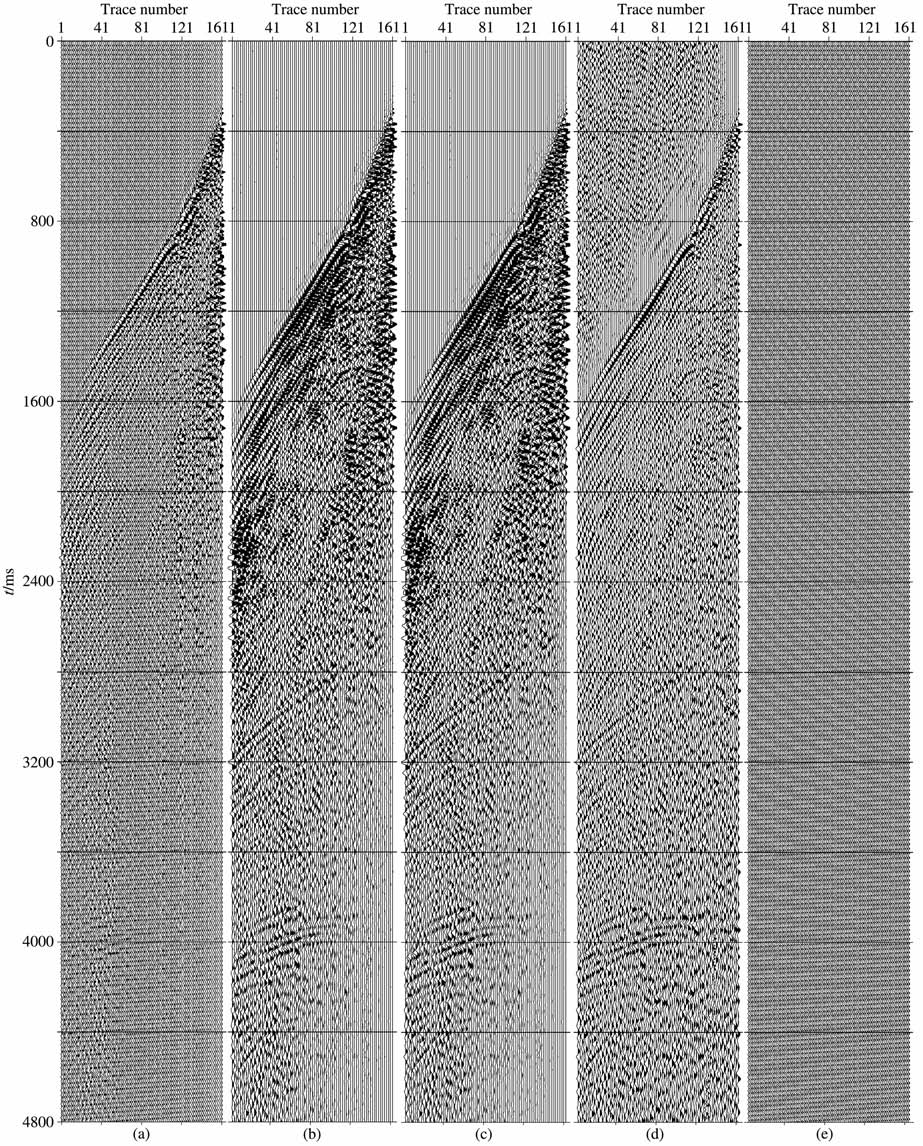
使用实际数据例子来说明余弦函数自相关法的可行性和有效性.实际数据是一个野外炮集数据，有180道，数据时间采样间隔是2 ms, 数据记录长度是6000ms.图 4是自相关法与自适应法^[14]炮集数据对比.图 5 是自相关法炮集数据第81 道频谱对比.

图 4 自相关法消除单频干扰处理效果对比 (a)原始炮集数据；(b)自适应法；(c)自相关法纯波显示；(d)自相关法增益显示；(e)检测出的单频干扰. Fig. 4 Result comparison of the ACA for a real data (a) Raw； (b) IEAMI； (c) ACA( pure wave) ； (d) ACA( gain) ； (e) Detected MFI.

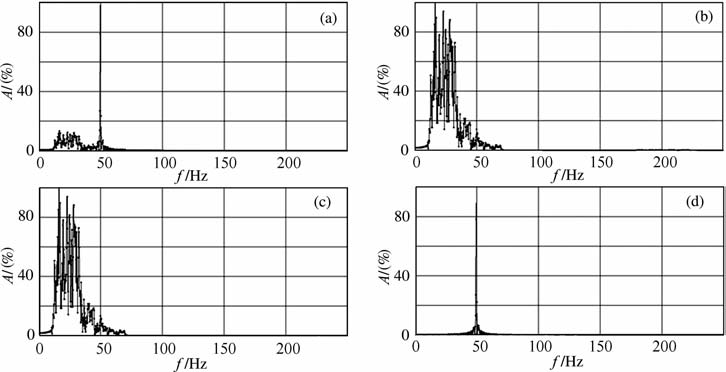
图 5 自相关法实际数据效果频谱对比 (a) 原始数据;(b) 自适应法;(c) 自相关法;(d) 检测的单频干扰. 它们的最大振幅值分别是5336753、3403400、3403281和5606054. Fig. 5 Spectrum comparison of the ACA results for a real seismic trace (a) Raw; (b) IEAMI; (c) ACA; (d) Detected MFI. Their maximum amplitude values are 5336753, 3403400, 3403281 and 5606054, respectively

显然原始数据中包含着很强的单频干扰，从频谱中也可以清楚地看到单频干扰.从数据以及频谱可以看到，自适应法和自相关法非常有效地消除了地震数据上的单频干扰.对一个1.6G 共130559道的地震数据进行运算效率对比，自适应法运算花费的时间是2236s, 自相关法是321s, 是自适应法运算时间的1/7，自相关法大大提高了运算效率，节省运算时间，更加适用于海量地震数据处理需要.因此是消除单频干扰的最有效方法.

5 结论

自相关法单频干扰识别与消除方法，就是基于地震数据自相关函数，计算单频干扰余弦函数，基于余弦函数自适应减算法估算地震数据中的单频干扰.单频干扰的频率(和相位)参数与单频干扰呈现非线性函数关系，因此任何估算方法都非常费时，而本方法不需要估算单频干扰的频率､相位和振幅参数，可以快速确定单频干扰，以达到消除单频干扰的目的.它是单频干扰消除算法中最有效的方法之一.理论数据和实际数据处理表明，该方法在压制单频干扰时不会伤害其他频率成分的有效信号波，在干扰存在的频率成分上有效信号保存完好，且计算效率大为提高，是目前高覆盖､高密度3D地震数据处理中消除单频干扰最经济､有效的手段.

致谢

在方法研究过程中，得到了东方地球物理公司物探技术研究中心领导和处理方法研究部同事的支持和帮助，在此一并表示衷心的感谢!

参考文献

[1]	黄绪德. 排除输电线干扰. 石油物探 , 1977, 26(4): 1–15. Huang X D. Elimination of power line interference wave. Geophysical Prospecting for Petroleum (in Chinese) , 1977, 26(4): 1-15.

[2]	石油物探研究大队修配厂. 自动频率跟踪陷波器. 石油物探 , 1978, 27(2): 17–30. Reparative worker of oil geophysical prospecting research. Autofreuency tracing notch filter. Geophysical Prospecting for Petroleum (in Chinese) , 1978, 27(2): 17-30.

[3]	宋祈真. 输电线对地震勘探的干扰及排除. 石油地球物理勘探 , 1979, 14(2): 54–60. Song Q Z. Power line interference and elimination for seismic prospecting. Oil Geophysical Prospecting (in Chinese) , 1979, 14(2): 54-60.

[4]	孙文森. 无相位畸变的50. Hz干扰滤波器. 电测与仪表 , 1980, 17(4): 24–25. Sun W S. A 50 Hz interference filter of phase distortionlessness. Electrical Measurement and Instrumentation (in Chinese) , 1980, 17(4): 24-25.

[5]	王本吉, 狄邦让. 窄带自动跟踪陷波器. 石油地球物理勘探 , 1985, 20(4): 411–414. Wang B J, Di B R. Narrow band autotrack notch filter. Oil Geophysical Prospecting (in Chinese) , 1985, 20(4): 411-414.

[6]	郭其贵. 一种50. Hz陷波器的设计及效果. 石油地球物理勘探 , 1988, 23(5): 626–629. Guo Q G. Design and effect of a 50 Hz notch filter. Oil Geophysical Prospecting (in Chinese) , 1988, 23(5): 626-629.

[7]	凌云, 郭向宇. 非地表一致性噪声的压制. 石油地球物理勘探 , 1992, 27(1): 13–28. Ling Y, Guo X Y. Method for suppressing the non-surface-consistent noise. Oil Geophysical Prospecting (in Chinese) , 1992, 27(1): 13-28.

[8]	高少武, 周兴元, 蔡加铭. 时间域单频干扰波压制. 石油地球物理勘探 , 2001, 36(1): 51–55. Gao S W, Zhou X Y, Cai C M. Suppression of single-frequency interference wave in time domain. Oil Geophysical Prospecting (in Chinese) , 2001, 36(1): 51-55.

[9]	刘洋. 强工频干扰波的提取与消除方法. 石油物探 , 2003, 42(2): 154–159. Liu Y. Extraction and removal of strong power interference. Geophysical Prospecting for Petroleum (in Chinese) , 2003, 42(2): 154-159.

[10]	Sauicer A, Marchant M, Chouteau M. A fast and accurate frequency estimation method for canceling harmonic noise in geophysical records. Geophysics , 2006, 71(1): 7-18.

[11]	Nyman D C, Gaiser J E. Adaptive rejection of high-line contamination. Expanded Abstracts of 53^rd Annual Internat SEG Mtg,1983. 321~323

[12]	Karl E. Butler, Russell R. Don.. Subtraction of powerline harmonics from geophysical records. Geophysics , 1993, 58(6): 898-903. DOI:10.1190/1.1443474

[13]	高少武, 贺振华, 赵波, 等. 时间域单频干扰波消除方法的改进. 石油地球物理勘探 , 2008, 43(3): 270–274. Gao S W, He Z H, Zhao B, et al. Improvement of method eliminating single-frequency interference wave in time domain. Oil Geophysical Prospecting (in Chinese) , 2008, 43(3): 270-274.

[14]	高少武, 贺振华, 赵波, 等. 自适应单频干扰波识别与消除方法研究. 石油物探 , 2008, 47(4): 352–356. Gao S W, He Z H, Zhao B, et al. Identification and elimination of adaptive monofrequency interference wave. Geophysical Prospecting for Petroleum (in Chinese) , 2008, 47(4): 352-356.

[15]	罗国安, 高少武, 魏庚雨, 等. Chirp-Z变换谱分析压制地震记录单频干扰. 石油地球物理勘探 , 2009, 44(2): 166–172. Luo G A, Gao S W, Wei G Y, et al. Suppression of mono-frequency interference on seismic record by Chirp-Z transform spectrum analysis. Oil Geophysical Prospecting (in Chinese) , 2009, 44(2): 166-172.

[16]	高少武, 赵波, 贺振华, 等. 基于余弦函数的自适应单频干扰消除. 地球物理学进展 , 2009, 24(5): 1762–1767. Gao S W, Zhao B, He Z H, et al. Elimination of adaptive monofrequency interference based on cosine function. Progress in Geophysics (in Chinese) , 2009, 24(5): 1762-1767.

[17]	高少武, 罗国安, 赵波, 等. 利用线性调频谱法识别与消除单频干扰. 石油地球物理勘探 , 2010, 45(6): 861–867. Gao S W, Luo G A, Zhao B, et al. Utilizing linear frequency modulation spectrum method to identify and remove single-frequency interference. Oil Geophysical Prospecting (in Chinese) , 2010, 45(6): 861-867.

[18]	Rabiner L R, Schafer R W, Rader C M. The Chirp z-Transform Algorithm. IEEE trans, Audio Electro-acoustics , 1969.

[19]	徐平, 王宝善, 张尉, 等. 利用互相关函数求地震波衰减. 地球物理学报 , 2006, 49(6): 1738–1744. Xu P, Wang B S, Zhang W, et al. Estimating seismic attenuation using cross-correlation function. Chinese J. Geophys. (in Chinese) , 2006, 49(6): 1738-1744.

[20]	陆斌, 葛洪魁, 吴何珍, 等. 利用相关域小波变换进行SWD资料预处理. 地球物理学报 , 2009, 52(9): 2349–2356. Lu B, Ge H K, Wu H Z, et al. SWD data preprocessing using wavelet transform of correlation domain. Chinese J. Geophys. (in Chinese) , 2009, 52(9): 2349-2356.

[21]	奥本海姆A V, 谢弗R W. 离散时间信号处理. 北京: 科学出版社, 1998 : 576 -588. Oppenheim A V, Schafer R W. Discrete Time Signal Processing (in Chinese). Beijing: Science Press, 1998 : 576 -588.


地球物理学报 2011, Vol. 54 Issue (3): 854-861	PDF