2. 中国科学院研究生院,北京 100049
2. Graduate University of Chinese Academy of Sciences, Beijing 100049, China
随着勘探目标变得更复杂以及岩性成像的需要,波动方程叠前深度偏移正在生产中得到广泛应用.波动方程叠前深度偏移的核心是用波动理论描述地震波在地下复杂构造中的传播,进而剔除传播效应,获得地下构造的反射强度图像.偏移速度模型是正确描述地震波传播效应的关键.偏移算法与速度模型是对应的,偏移成像的关键是剔除传播效应,只有偏移算法与这一速度模型结合能正确反映地震波的传播效应,这一速度模型才是合适的.因此,偏移速度模型并不要求是地下介质的真实速度,一般而言,它是实际速度的平滑近似.因而,偏移速度模型更严格的称之为宏观速度模型.采用宏观速度模型进行偏移就导致对一种偏移算法较为合适的偏移速度模型(即可以将同相轴拉平),对另一种算法就不一定是最佳的.
已发展的一些偏移速度建模方法,包括基于地震波走时速度分析方法[1, 2]、基于波动方程的层析成像方法[3]、基于双程波动方程的非线性波形反演方法[4, 5]和基于波动方程偏移的速度分析方法[6~9].尽管非线性波形反演和波动方程偏移速度分析方法展示了很好的前景,目前工业界使用的主流方法仍是基于地震波走时的速度分析方法,包括同时拾取走时和入射角方向的层析成像方法、拾取共聚集算子的共聚集点(CFP)方法、和克希霍夫积分(KKF)偏移的速度分析方法.层析成像方法的核心是使得射线的计算走时与在地震记录中拾取的相同,CFP方法的核心是使得基于CFP 算子合成的CFP 道集与CFP算子有相同的走时,偏移速度分析的核心是将共成像点的同相轴拉平.
将基于地震波走时速度分析方法得到的速度模型应用于波动方程偏移,就可能产生前面讨论的问题:尽管速度模型可能使积分法偏移的同相轴平直,但它并不一定保证波动方程偏移得到的同相轴也是平直的.波动方程偏移速度建模方法需要进行多次波动方程偏移计算,完全基于波动方程偏移方法进行速度建模目前还难以实现.一个更有效、可行的方案是:首先应用基于地震波走时的速度分析方法建立一个初始的速度模型,然后通过修改速度模型,形成适合波动方程偏移的宏观速度模型.这就是本文的研究思路.实际上,本文方法所使用的初始速度模型的来源可更广泛,将叠前时间偏移得到的叠加速度模型进行Dix反演并做时深转换,就可作为本文方法的初始速度模型.
应用波动方程偏移进行速度建模的一个主要困难是偏移过程中一般不保留偏移距信息,这样就不能得到定量反映偏移速度误差的成像同相轴.基于双平方根算子的偏移方法理论上可以保留偏移距信息,但由于其涉及的空间维数较多,带来了巨大的计算量,若不引入某些近似(如共方位角偏移),就难以应用于实际生产.形式上,炮域偏移可给出随炮点位置变化的共成像点道集,但单炮的偏移结果实际上混合了不同的偏移距,这一道集不能定量给出偏移速度的误差;当偏移速度的误差较大时,有时在这一道集上甚至找不到同相轴.
Sava等人[10]提出的波动方程偏移生成角道集技术,为波动方程偏移速度建模展现了新的途径.这一技术从炮域偏移出发,得到了随与界面法线夹角变化的共成像点道集---角道集,这一道集可定量反映偏移速度的误差.正如我们在文中论述的那样,基于炮域偏移产出角道集的技术,其实质是用单平方根算子的波场延拓实现了双平方根算子计算,因此所产生的角道集保留并利用了偏移距信息.从角道集出发,现行的波动方程偏移速度建模将速度建模作为一个反问题,即求速度场,使得全部角道集中同相轴的曲率最小(即同相轴被拉平).求解这样一个反问题需要多次的炮域波动方程偏移计算,尽管集群计算机的发展已使三维波动方程偏移成为可能,但多次迭代,特别是初始模型不理想情况导致的收敛速度较低,限制了这一技术的实际应用.为减少计算量,逐层剥离法是各类偏移速度建模方法普遍采用的技术,但该方法会导致误差扩散,降低了其处理速度横向剧烈变化的能力.
本文沿用角道集技术,通过给出非均匀介质中角道集中同相轴曲率与速度误差的定量关系,发展了一个直接的速度模型更新方法.为避免像逐层剥离法那样将浅层的误差累积扩散至深层,本文对每一水平分析点采用上、下同时计算的最小二乘速度校正方法.在初始模型较合理的情况下,应用一次炮域波动方程偏移计算,本文方法即可得到较准确的、适用于波动方程偏移的速度模型.本文方法可用于解决由地震波走时技术求得的速度模型与波动偏移方法不匹配的问题,避免了直接由波动方程偏移进行速度建模所需要的多次偏移计算.数值结果证明了本文方法的有效性.
2 波动方程偏移生成角道集三维叠前地震数据可看做是由二个炮坐标、二个检波点坐标(或二个共中心点坐标、二个方向的偏移距)和一个时间坐标构成的五维数据体.双平方根算子可直接对这一五维数据体进行波场延拓,得到不同偏移距数据的成像结果.但即使对层状介质,这一五维数据体的波场延拓涉及五重正反傅氏变换,计算量仍难以承受.而炮域数据是三维叠前数据的一个自然的分解,它将五维数据体分解为若干个三维数据体;层状介质情况下,基于炮域数据的成像仅涉及若干个三重正反傅氏变换,计算效率大大提高.因此,除对三维叠前地震数据采用某种近似(如共方位角),一般均采用炮域数据进行偏移计算.
炮域波动方程偏移应用单平方根算子,单炮数据在一个成像点只有一个结果;而这一结果实际上是该炮中不同偏移距数据的叠加,因此没有独立的偏移距信息.尽管炮域偏移可给出随炮点位置变化的共成像点道集,但这一道集不能定量反映偏移速度的误差;当偏移速度的误差较大时,有时在这一道集上甚至找不到同相轴.这一困境,使得长期以来没法应用炮域偏移进行偏移速度分析.Sava等人的一系列工作破解了这一困境.他们通过修改炮域波动方程偏移的成像条件为
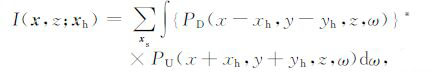
|
(1) |
式中PD 和PU 分别是深度延拓后频率域炮点和检波点波场,xh = (xh, yh)是引入的偏移距参数,累加是针对全部炮xs 的偏移结果进行.Sava等[11]建议,对成像结果I(x,z;xh)中的参数xh 进行一个变换,即可得到I(x,z;θ),而tanθ= |kh| /|km| ;这里kh 和km 分别是xh 和x对应的波数向量,而θ 就是波场入射方向与界面法向的夹角.
角道集I(x,z;θ)定量反映了偏移速度的误差.当偏移速度正确时,角道集的同相轴是水平的;当偏移速度过大时,同相轴向下弯曲;当偏移速度过小时,同相轴向上弯曲.式(1)的成像条件为什么能得到角道集?Sava等并没给出理论证明.实际上,(1)式的结果是与基于双平方根算子的波场延拓存在密切联系[12].定义函数
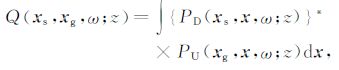
|
(2) |
式中PD 和PU 同(1)式,分别是不同深度上的炮点和检波点波场,它们满足单程波方程,函数变量中的两个向量代表三维叠前地震数据的四个空间坐标.当z=0,PD =δ(x-xs),而PU =F(xg, x,ω)是炮点在x的单炮记录;这样由(2)式可得,Q= F(xg, xs, ω),即函数Q(z=0)就是地表记录的三维叠前地震数据.对(2)式求z的导数,得
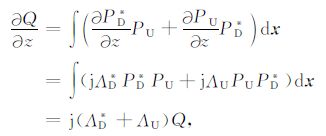
|
(3) |
式中ΛU 和ΛD 分别是炮点和检波点波场深度延拓对应的单程波算子,而ΛD* +ΛU 则对应着双平方根算子.这表明由(2)式得到的Q(z)满足双平方根方程,既然已证明Q(z=0)是地表记录的三维叠前地震数据,因此Q(xs, xg, ω;z)实际上就是叠前地震数据应用双平方根方程延拓到深度z上的结果.
对Q(xs, xg, ω;z)应用零时刻成像条件,再将炮点和检波点坐标分别用中心点x和半偏移距xh 表示,可得深度z上不同偏移距的成像结果为

|
(4) |
对比式(1)可知,式(1)中的I(x,z;xh)就是不同半偏移距xh 的成像结果.第3节将证明,将半偏移距通过倾斜叠加或局部傅里叶转换,即可得到角度域成像道集.对比(4)式和(1)式也表明,若应用式(1)计算角道集,炮点需足够密且排列均匀,只有这样(2)式中的积分才能与(1)式中的求和等价.式(3)的推演还表明,基于双平方根方程的成像,实际上默认了震源使用空间和时间脉冲,采用相关成像条件成像.
3 同相轴曲率与偏移速度误差角道集是否平直反映了偏移速度是否正确.因此由(1)式得到的角道集为波动方程偏移速度建模提供了基础.一个自然的做法是:求速度场使得全部角道集中同相轴的曲率最小,这就是现行的非线性反问题求解方案;但这一方案涉及多次的炮域波动方程偏移计算,计算量极大,且不一定保证收敛.本文则通过定量给出角道集中同相轴曲率与速度误差的关系,发展了一个直接的速度模型更新算法.在推导这一定量关系时,文中假设介质速度是横向不变的;而通过允许不同水平位置有不同的速度,再应用横向插值,是可以较好处理速度横向非均匀的.实际上,现行的单程波方程求解和偏移速度建模,都是沿用了这一思路.
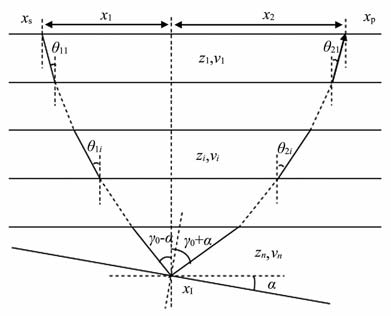
图 1给出横向均匀的模型,为使导出的定量公式能正确处理实际的横向非均匀介质,模型中考虑了反射界面不是水平的情况;不失一般性,考虑二维情况下一个炮检对(即单道数据)的情况,地震波由xs 点下传至倾斜界面,反射至xp, 反射界面的倾角是α,用水平层状介质来表示速度的纵向变化,各层的厚度与速度分别为zi和vi;图中虚线代表了穿过多个介质层.设地震波由xs 至xp 传播的走时为τ0 ,幅值为A0,则脉冲震源作用下xp 的接收信息为A0exp(-jωτ0).下面对这一仅有一个接收道的单炮(即一个炮检对)应用波动方程偏移方法和(1)式进行成像;令图 1中成像点xI 为横向坐标原点.
|
图 1 深度偏移速度模型波场传播及成像示意图 Fig. 1 Illustration of wave propagation and imaging |
假设介质速度横向均匀,采用相移法,频率波数域的震源波场延拓可表达为
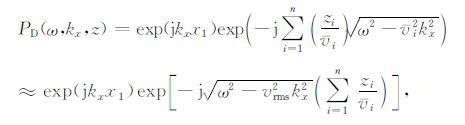
|
(5) |
式中vi是采用的偏移速度,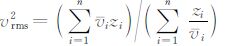
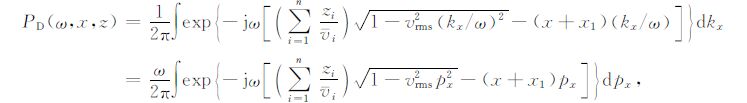
|
(6) |
式中px=kx/ω 是射线参数,与频率无关.因此(6)式可应用稳相点原理求得渐近解为[13]
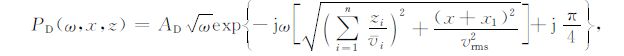
|
(7) |
其中振幅项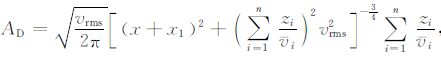
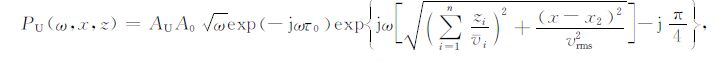
|
(8) |
其中振幅项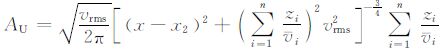
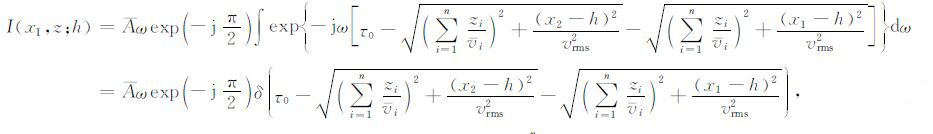
|
(9) |
式中A =ADAUA0,h为所定义的半偏移距,而成像深度
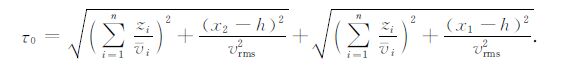
|
(10) |
图 2给出了图 1 层状介质下单个炮检对数据应用相移法和式(1)成像条件得到的x=0处实际半偏移距成像结果.如式(10)表达的一样,对应了(z,h)平面上的一条近似斜线.通过倾斜叠加进行角度变换时,这个斜线的斜率就对应了角度的正切值,而h=0时深度z对h的导数就代表了这一斜线的斜率.

|
图 2 半偏移距成像结果 Fig. 2 Half-offset image gathers |
由式(5)的均方根速度定义和式(9)的深度z定义可得:
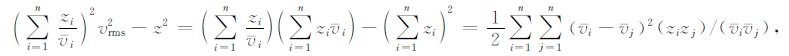
|
(11) |
式中的右端项是一个与速度梯度有关的正小量,我们定义其为R,将(11)式代入(10)式可得深度z对h的导数为
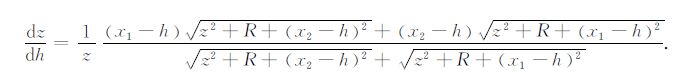
|
(12) |
层状介质假设下利用Snell定律,如图 1所示,可得到x1 和x2 与反射点深度与入射角的关系:
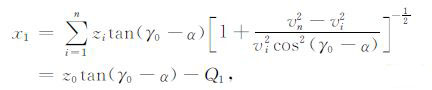
|
(13) |

|
(14) |
式中z0 为实际反射点的真实深度,γ0 为真实入射角,vi是如图 1所示的真实速度,Q1 和Q2 均为与真实速度的变化梯度有关的一个小量,速度梯度为正时这一小量为正,速度梯度为零时它们为零.
将(13)和(14)式代入式(12)且令h=0,可得成像结果在角道集中对应角度的正切值:

|
(15) |
其中
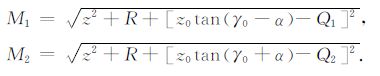
|
当使用正确的偏移速度进行偏移时,即vi=vi,则有成像深度z=z0,将这两个条件代入(15)式,可得
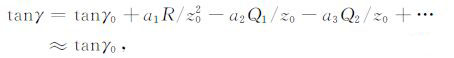
|
(16) |
式中a1,a2 等为与角度γ0 和α 有关的系数.式(16)中在速度梯度不是很大时有很好的精度.式(16)表明,采用(1)式的成像条件并利用倾斜叠加进行角度变换,可将图 1中的单道数据偏移成为角度为γ0 的角道集中的一个成像道,而由图 1 可知,γ0 恰好是入射波与界面法线的夹角.这从理论上证明了,采用(1)式成像条件并结合角度变换,可由炮域偏移得到入射线与界面法线夹角的入射角角道集.下面我们将进一步给出角道集中同相轴弯曲与偏移速度误差的定量关系.
式(10)中的τ0 是常量,不随偏移速度变化;若令h=0,当偏移速度不是图 1中所示的速度,即vi≠vi,可由式(10)得
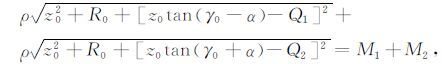
|
(17) |
式中ρ=vrms/vrms0, 而vrms0 是由真实速度vi按式(5)计算的均方根速度,R0 是类似于(11)式的小量.联立(15)和(17)式,并对根号项进行泰勒展开近似,可解得:
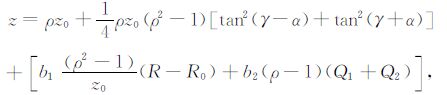
|
(18) |
式中b1,b2 是与角度γ 和α 有关的系数;当速度梯度不是很大时,式中右端的最后一项是个小量.当ρ =1时,即采用真实速度进行偏移,由式(18)得z=z0,这表明深度为一与角度无关的常量,因此角道集中的同相轴是平直的.
当ρ≠1时,可由(18)式求得同相轴的剩余动校量:
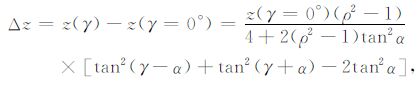
|
(19) |
式中z(γ=0°)为γ=0°时对应的深度z,用它替换z0 是因为实际偏移中我们并不知道真实的深度.若忽略地层倾角,即假设α=0°,可进一步得到简化的剩余动校正量公式:
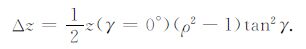
|
(20) |
利用(19)或(20)式,即可由角道集中同相轴的弯曲程度直接求得ρ,进而得到真实速度对应的均方根速度vrms0.第4 节将给出利用vrms0反演vi的方法.式(19)或(20)是本文直接的速度模型更新算法的核心,它避免了通过多次炮域波动方程偏移,来实现角道集中同相轴的平直,进而得到偏移速度的冗长计算.
文献[14]与[15]中给出均匀介质情况下角道集中同相轴曲率与速度误差的定量关系,但这一关系在应用中存在两个问题,一是实际的非均匀介质情况下如何应用,二是该关系式中剩余动校量是沿反射界面法向拾取的.沿法向拾取剩余动校量要求相邻像点的角道集存在,而实际上,采用(1)式成像条件生成角道集需较多的内存(二维情况成像数据体增加了一维,三维时增加了二维),实际应用中不可能逐个成像点均产出角道集;而从速度估计的角度出发,逐点产出角道集也是不必要的.式(20)避免了这两个问题,使得基于拾取剩余动校量的反演成为可能.第5节的数值算例将表明,界面有较大倾斜时这一定量关系也有很好的精度.
4 速度更新对角道集中的同相轴,由不同的ρ 值用式(19)或(20)计算剩余动校量并进行校正,然后横向叠加,可得到随ρ 变化的能量图(如图 6 所示);由此图可根据最大能量团位置直接拾取不同深度同相轴对应的ρn,进而得到该深度处的准确均方根速度vrmsn为
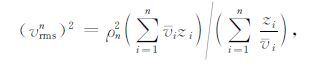
|
(21) |
式中zi是依据同相轴进行层位解释时得到的各层厚度,vi是该层对应的偏移速度.本文建议了两种偏移速度更新方法,一是在各层位处设置偏移速度的修正系数ri,而两个层位间速度的修正系数由ri和ri+1 线性插值得到;二是对每一层位定义一个惟一的修正系数ri.前者适用于层间速度按梯度变化情况,后者适用于层间速度是常量的情况.以第一种算法为例,由修正系数ri,可得速度更新后的均方根速度为
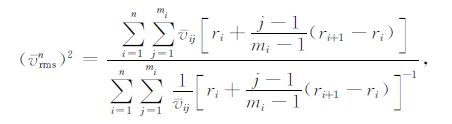
|
(22) |
式中mi是各速度层中深度采样点数,vij是第i层中第j个像点的实际偏移速度.定义误差函数J=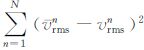
对不同水平位置的角道集求得对应的ri,对所有ri进行空间平滑和插值,可形成修正系数的空间数据体.用这一数据体乘上原来的偏移速度,即实现了速度更新.整个过程只需要进行一次波动方程偏移,且只需在远大于共中心点(CMP)间距的等间距节点上生成角道集.由于该方法并不对初始速度模型构造进行大的改动,主要针对初始速度模型的局部速度值进行修正而达到拉平偏移道集的效果,因此要求初始速度模型能够大体反映地下构造.第5节的理论和实际数据例子表明这一速度更新方法是有效的.
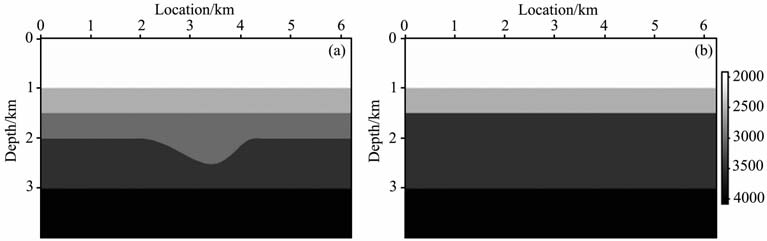
5 数值算例与实际应用 5.1 理论模型数据为验证本文方法,我们设计了如图 3a所示的理论模型,该速度模型具有横向变速和最大地层倾角为45°的结构,对这一模型应用声波方程数值模拟方法[16]产生一组理论数据集,共195 炮.假设的初始速度模型如图 3b,对比可知两者有较大的差异.图 4a是基于初始速度模型的波动方程偏移叠加剖面;按空间间距125m 求取得角道集.图 4b是由梯度张量法[17]求得的偏移剖面上同相轴的倾角.
|
图 3 (a)实际速度模型和(b)初次偏移所用速度模型 Fig. 3 Accurate velocity model (a) and original migration velocity model (b) |

|
图 4 (a)初次偏移结果和(b)地层倾角扫描结果 Fig. 4 Migrated image by original velocity (a) and geologic dip (b) |
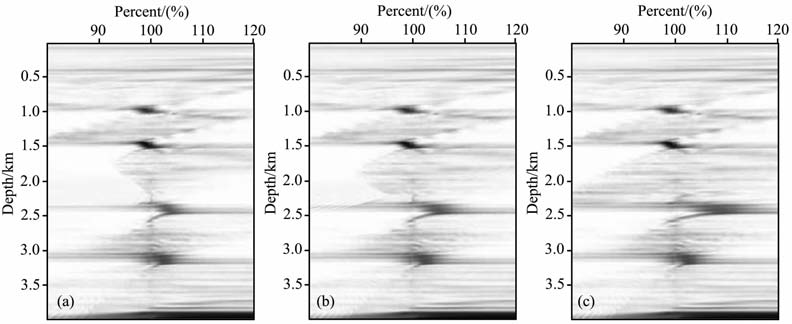
图 5是2.75km 处的角道集,从图上可看出深层两个界面对应的同相轴发生了弯曲.由图 3a可知,第三个同相轴对应了有较大倾角的反射界面(26°).我们将以这一角道集为例,分析本文剩余动校量公式的准确性.利用实际速度模型和初始速度模型,可在理论上得到该道集2.4km深度处(对应第三个同相轴)的均方根速度误差为1.032;图 6a、6b和6c分别给出利用公式(19)、文献[14]的公式以及忽略界面倾角的式(20)的参数ρ 扫描结果;为应用文献[14]的公式,必须重新加密计算角道集.由图 6a知,第三个同相轴对应的ρ恰为1.032,而文献[14]公式的扫描结果为1.048,式(20)扫描结果的能量团有些散,ρ 可近似取为1.089.图 6的比较表明,界面倾角较大时倾角影响不能忽略,而本文公式在界面有较大倾斜时也有很好的精度.

|
图 5 典型的角道集 Fig. 5 Typical angle gathers |
|
图 6 参数,ρ扫描结果,其中(a)对应式(19),(b)对应文献[10],(c)对应式(20) Fig. 6 Parameter ,ρ obtained using (a)Eq. (19),(b) Ref. [10] and (c) Eq. (20) |
图 7中间的灰度图为应用一次本文方法得到的更新后的速度模型.图中分别列出了深度为1.9km处沿横向和横向位置2.75km 和3.9km 处沿垂向的更新前后速度对比,位置如灰度图中实线所示.其中a为真实速度,b为初始偏移速度,c为更新后的速度.可以看出本文方法得到的偏移速度与真实速度基本吻合,初始速度模型中不存在的弯曲界面被正确恢复.

|
图 7 速度模型更新结果和速度对比其中a为正确速度,b为初始偏移速度,为速度更新后结果. Fig. 7 Updated velocity model a Accurate velocity; b Original velocity; c Updated velocity. |
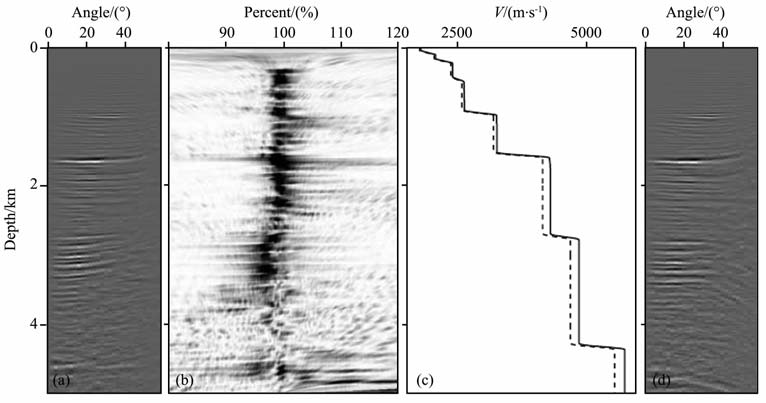
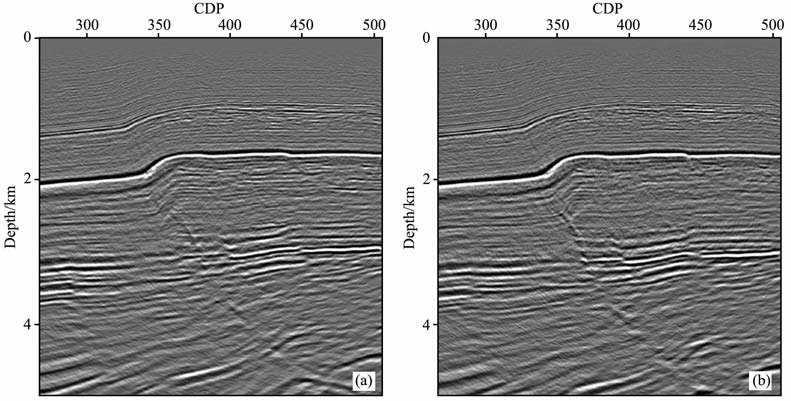
将本文方法应用于某陆上三维数据,得到较好效果.图 8a为应用初始速度模型偏移后得到的某一道角道集,可以看出此处的偏移速度偏小,同相轴向上弯曲.图 8b为参数ρ 的扫描结果,籍此我们可拾取各同相轴对应的均方根速度误差.图 8c为更新前后该角道集位置上偏移速度沿深度方向的对比,其中虚线为初始速度,实线为更新后速度.图 8d为应用更新后的速度重新偏移得到的角道集,可发现原来向上弯曲的同相轴基本已被拉平,这表明更新后的偏移速度模型是合适的.当生成角道集后,本文方法的应用仅涉及单个道集,与模型大小、二维或三维没有关系,因此使用上较简单.图 9a是应用初始速度模型进行偏移得到的某一条地震剖面,可以看到由于速度不准确,断层的断面不够清晰,断面波也并没有收到相应位置而是与同相轴产生交叉;图 9b为应用更新后速度模型进行偏移得到相同位置的偏移结果,在图中可见断面更加清晰,断面波也已经收到对应位置.上述的结果表明本文方法在实际应用中是很有效的.
|
图 8 实际角道集数据应用效果(a)为初始速度对应的角道集,(b)为参数p扫描结果,(c)为更新前后速度对比,(d)为更新后速度得到的角道集. Fig. 8 Practical application of this approach to angle gathers (a) Angle gather from original velocity; (b) Parameter (c) Original and updated velocity;(d) New angle gather from updated velocity. |
|
图 9 实际数据应用效果(a)为初始速度对应的偏移剖面,(b)为应用更新后速度得到的偏移剖面. Fig. 9 Practical application of this approach(a) Migration profile from original velocity; (b) Migration profile from updated velocity. |
本文从理论上证明了现行的由炮域波动方程偏移求角度域成像道集方法的正确性.给出了非均匀介质情况下角道集同相轴曲率与偏移速度误差的定量关系;这一定量关系将同相轴曲率的拾取限定在单个角道集,避免了跨角道集拾取对角道集空间密度的过高要求.以这一定量关系为基础,文中建议了一种波动方程偏移速度更新的直接反演方法.反演计算是逐道集进行,计算量很小.本文方法计算简单、不需迭代,在初始模型较合理的情况下,应用一次炮域波动方程偏移计算,即可得到较准确的、适用于波动方程偏移的速度模型.这一工作较好地解决了由走时层析成像等方法得到的速度模型与波动偏移方法不匹配的实际问题.理论和实际数据例子证明了本文方法的有效性.
| [1] | Bishop T N, Bube K P, Cutler R T, et al. Tomographic determination of velocity and depth in laterally varying media. Geophysics , 1985, 50: 903-923. DOI:10.1190/1.1441970 |
| [2] | Liu Z Y, Bleistein N. Migration velocity analysis: theory and an iterative algorithm. Geophysics , 1995, 60: 142-153. DOI:10.1190/1.1443741 |
| [3] | Luo Y, Schuster G T. Wave-equation traveltime inversion. Geophysics , 1991, 56: 645-653. DOI:10.1190/1.1443081 |
| [4] | Tarantola A. A strategy for nonlinear elastic inversion of seismic reflection data. Geophysics , 1986, 51: 1893-1903. DOI:10.1190/1.1442046 |
| [5] | Dessa J X, Operto S, Kodaira S, et al. Multiscale seismic imaging of the eastern Nankai trough by full waveform inversion. Geophysical Research Letters , 2004, 31: L18606-L18609. DOI:10.1029/2004GL020453 |
| [6] | Sava P C, Bindi B, Etgen J. Wave-equation velocity analysis by focusing diffractions and reflections. Geophysics , 2005, 70: U19-U27. DOI:10.1190/1.1925749 |
| [7] | Halpert A D, Clapp R G, Lomask J, et al. Image segmentation for velocity model construction and updating. 78th Annual International Meeting, SEG, Expanded Abstracts, 2008: 3088~3092 |
| [8] | Bevc D, Fliedner M M, Biondi B. Wavepath tomography for model building and hazard detection. 78th Annual International Meeting, SEG, Expanded Abstracts, 2008: 3098~3102 |
| [9] | 刘奇琳, 刘伊克, 常旭. 双平方根波动方程偏移速度分析. 地球物理学报 , 2009, 52(7): 1891–1898. Liu Q L, Liu Y K, Chang X. Wave-equation migration velocity analysis by Double Square Root method. Chinese J. Geophys. (in Chinese) , 2009, 52(7): 1891-1898. |
| [10] | Sava P C, Fomel S. Angle-domain common-image gathers by wavefield continuation method. Geophysics , 2003, 68: 1065-1074. DOI:10.1190/1.1581078 |
| [11] | Sava P C, Fomel S. Coordinate-independent angle-gathers for wave equation migration. 75th Annual International Meeting, SEG, Expanded Abstracts, 2005: 2052~2057 |
| [12] | Zhang Y, Xu S, Bleistein N, et al. True-amplitude angle-domain common-image gathers from one-way wave-equation migration. Geophysics , 2007, 72: S49-S58. DOI:10.1190/1.2399371 |
| [13] | 李世雄. 波动方程的高频近似与辛几何. 北京: 科学出版社, 2001 . Li S X. High-Frequency Asymptotic Solution and Symplectic Geometry of Wave Equation (in Chinese). Beijing: Science Press, 2001 . |
| [14] | Biondi B, Symes W W. Angle-domain common-image gathers for migration velocity analysis by wavefield-continuation imaging. Geophysics , 2004, 69: 1283-1298. DOI:10.1190/1.1801945 |
| [15] | Stork C C. Reflection tomography in the postmigrated domain. Geophysics , 1992, 57: 680-692. DOI:10.1190/1.1443282 |
| [16] | 徐义, 张剑锋. 地震波数值模拟的非规则网格PML吸收边界. 地球物理学报 , 2008, 51(5): 1520–1526. Xu Y, Zhang J F. An irregular-grid perfectly matched layer absorbing boundary for seismic wave modeling. Chinese J. Geophys. (in Chinese) , 2008, 51(5): 1520-1526. |
| [17] | van Vliet L J,Verbeek P W. Estimators for orientation and anisotropy in digitized images. Proceedings of the First Conference of the Advanced School for Computing and Imaging, Heijen (The Netherlands). 1995:442~450 |
 2011, Vol. 54
2011, Vol. 54

