地球物理学报  2011, Vol. 54 Issue (3): 828-834   PDF    
引用本文
李振华, 王彦飞, 杨长春. 正则化偏移成像的全局优化快速算法. 地球物理学报, 2011, 54(3): 828-834, doi: 10.3969/j.issn.0001-5733.2011.03.023.  
LI Z H, WANG Y F, YANG C C. A fast global optimization algorithm for regularized migration imaging. Chinese J. Geophys. (in Chinese), 2011, 54(3): 828-834, doi: 10.3969/j.issn.0001-5733.2011.03.023.  
正则化偏移成像的全局优化快速算法
李振华1,2 , 王彦飞1 , 杨长春1     
1. 油气资源研究重点实验室,中国科学院地质与地球物理研究所, 北京 100029;
2. 中国科学院研究生院,北京 100049
收稿日期 2010-03-31, 2011-02-12 收修定稿
基金项目: 国家自然科学基金项目(10871191,40974075),中国科学院知识创新工程重要方向性项目(KZCX2-YW-QN107)和国家重点基础研究发展规划(973)项目(2005CB422104)联合资助.
作者简介: 李振华,男,1984年生,2007年毕业于中国科学技术大学少年班系信息科学与计算数学专业,现为博士研究生,主要从事油储地球物理研究. E-mail:lizhenhua@mail.igcas.ac.cn
通讯作者: 王彦飞,男,研究员,1997年毕业于河北师范大学数学系,主要从事数学物理、信号/图像处理、计算地球物理以及其他地球科学的反演问题理论及计算研究. E-mail:yfwang@mail.iggcas.ac.cn;yfwang_ucf@yahoo.com
摘要: 目前,偏移后的地震剖面往往只是一个地质构造图像,还不能为后续的岩性分析和油气储层属性的提取提供更精确的信息.为了得到高分辨率真振幅的图像,建议采用正则化偏移成像方法.针对本问题数据规模大和正演算子矩阵稀疏的特点,提出采用一种新的算法——无记忆拟牛顿-模拟退火法对偏移算子方程进行求解.该方法综合了无记忆拟牛顿法优良的局部搜索能力以及模拟退火法的全局最优性质.用该方法得到的全局最优解不仅成像位置正确,还能提供更准确的振幅及其他属性信息.通过理论模型试算和实际资料处理,表明在正演算子准确的情况下,该方法能减弱Kirchhoff偏移的假象,得出接近真实的反射系数分布.因此,该方法在地震成像方面是有实际应用前景的.
关键词: 偏移      正则化      无记忆拟牛顿法      模拟退火法     
A fast global optimization algorithm for regularized migration imaging
LI Zhen-Hua1,2, WANG Yan-Fei1, YANG Chang-Chun1     
1. Key Laboratory of Petroleum Resources Research, Institute of Geology and Geophysics, Chinese Academy of Sciences, Beijing 100029, China;
2. Graduate University, Chinese Academy of Sciences, Beijing 100049, China
Abstract: At the present, seismic migration usually only yields an image of the positions of geological structures, and it cannot supply more accurate information for subsequent lithology analysis and attributes extraction. To get an image with high resolution and true amplitude, we suggest that regularized migration imaging should be used. Since the amount of cost for solving the problem is huge and the kernel matrix is sparse, we propose a new hybrid algorithm which is called Memoryless Quasi-Newton-Simulated Annealing Method. The algorithm not only shows as good performance in searching a local optimized solution as memoryless quasi-Newton method does, but also reaches the global optimized solution just as simulated annealing algorithm does. The global optimized solution obtained by this method not only gets the right positions, but also contains more reliable information for amplitude and other attributes. Theoretic simulations and field data applications are performed. It reveals that the proposed algorithm can attenuate the migration artifacts and provide a better frequency distribution of estimated reflectivity when a proper seismic modeling operator is constructed. Therefore, the proposed algorithm is very promising for seismic imaging..
Key words: Migration      Regularization      Memoryless Quasi-Newton method      Simulated annealing algorithm     
1 引言

地震偏移成像是反射地震学的核心内容，其中关键问题之一是处理不适定的反问题[1， 2].在工业生产中，为了计算迅速，通常都只是通过正演模型算子的共轭算子进行偏移成像.因此，在很多情况下，成像分辨率和振幅的保真度都有待提高[3].用共轭算子进行偏移，计算速度快，但是当共轭算子不能充分逼近逆算子时，我们一般需要通过迭代的方法进行更精确的求解.因而相继出现了最小二乘偏移[4]以及正则化偏移[5].但是偏移成像是一个独特的反问题，它的数据量巨大，蕴含不适定性，有效地迭代求解难度不少[6].目前在正则化偏移中应用的求解方法还停留于初级的数学技巧应用阶段，远远不能满足实际的需求.正则化偏移过程中，正则化项的形式，正则化因子的确定，最优化方法的选取，预处理技巧，停机准则等方面都有很大的改进空间.此外，计算效率也是一个很重要的课题.由此可见，研究快速求解此类问题的正则化方法十分重要.

Claerbout[7]指出Kirchhoff偏移算子不是正演模型算子的逆，而是它的共轭.为了消除Kirchhoff偏移在数据不完整时所产生的假象，Nemeth 等[4]建议采用最小二乘偏移，他们用预条件共轭梯度法求解其中带正则化项的最小二乘问题，选用对角预条件子，正则化项采用了数据误差服从高斯分布时的形式，但这些仅是很基础的数学技巧，还有更高级的技巧适应更复杂的情况[8].此后不久，Hu等[9]提出叠后偏移反褶积，Yu等[10]提出叠前偏移反褶积，他们都认为Kirchhoff偏移是一个模糊的图像，通过格林函数的计算，在偏移后应该再做一次反褶积，提高图像质量.同一时期，Lecomte[11]和Gelius[12]等提出分辨率函数的概念[11]，并在叠前深度偏移后进行分辨率补偿[12]，按Schuster等人的命名思路，他们的工作可以称为叠前深度偏移反褶积.这段时期这些学者相关的工作都可以看成是应用Kirchhoff偏移之后，分析出造成图像假象的原因，再求解一个最优化问题来修复原来模糊的图像.Sacchi等[5]进一步推广最小二乘偏移，提出正则化偏移，讨论了几种常见的正则化项，并指出正则化偏移将使地震偏移算法的发展迈进一个新时代.针对正则化偏移中求解最优化问题时计算技巧不足的情形，王彦飞等[13]阐述了地震偏移反演成像中的迭代正则化理论和方法并提出了正则化非单调梯度迭代法[14].

随着计算机运算速度和数学计算技巧等各方面的提高，以及并行计算的兴起，使原本耗时的正则化偏移成为可能.从常规偏移转换到正则化偏移这个崭新的领域，由于数据规模庞大，加上其不适定性和稀疏性，很多常用的初等的迭代最优化数学方法在这个领域已经不能适用.本文提出了一种新的混合型算法，即无记忆拟牛顿-模拟退火法(MQN-SA，Memoryless Quasi Newton-Simulated AnnealingAlgorithm)，该方法取长补短，综合两种方法的优势，能达到全局最优并有强大的局部搜索能力.

2 正则化偏移 2.1 正演模型算子

地震数据正演模型可以表述如下的第一类Fredholm 积分方程:

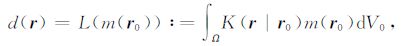
(1)

其中，m(r0)是地下的反射系数模型，d(r)是偏移要用到的输入数据(通常是地震剖面的形式)，K(r|r0)是受速度模型影响的核函数，Ω 是勘探范围内的三维空间.

在Born近似下，正演模型有如下的形式[15， 16]:

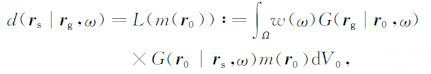
(2)

其中，w(ω)是频率域小波，G(rg|r0，ω)､G(r0|rs, ω)分别是从检波器到散射点的格林函数和从散射点到震源的格林函数，L就是所需的正演模型算子.

2.2 阻尼最小二乘偏移

经典的偏移概念一般是指使反射界面归位，绕射波收敛[17]；但是随着实际的应用以及观念的更新，偏移逐渐变成不仅仅是为了得到反映构造正确位置的剖面，人们还希望偏移后能得到诸如岩性､振幅等方面的准确信息.现在偏移的概念已经推广成为，从地震数据(经过常规处理后)到尽量与地下真实的地质剖面相接近的剖面所进行的操作.这就需要从(2)式中比较精确地求解m(r0).

当(2)式中的正演模型算子L不满足:LT ≈L-1 时，需要反演算法对(2)式进行反解[4].阻尼最小二乘偏移通过最小化如下的目标函数来得到地下的反射系数模型m(r0)=m:

(3)

其中，d是偏移要用的输入数据；C是作用到m上的一个线性算子，根据先验知识而定；m0 是关于模型的先验知识，即地下反射系数分布的一个初始模型；α 是阻尼因子.

2.3 正则化偏移

但是Sacchi等(2006)指出[5]，(3)式仅适用于模型参数服从正态分布时的情形.我们可以作进一步的推广而得到正则化偏移.正则化偏移通过最小化如下目标函数来得到地下的反射系数模型m(r0)=m[13]:

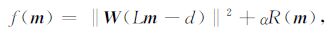
(4)

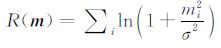
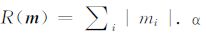
其中，d是偏移要用的输入数据；W是一个权重矩阵，得到它的一个途径是对需要偏移的地震数据进行自相关分析；R(m)被称为正则化项，它可以通过贝叶斯框架得到[5]，也可以从井数据的约束得到，也可以是某个具有地质意义的约束.例如，当模型参数服从高斯分布时就是(3)式的形式.当模型参数服从柯西分布时，则.当模型参数服从拉普拉斯分布时，则是正则化参数，可以先验选取，也可以通过后验计算获得[6].很明显，阻尼最小二乘偏移是一种特殊的正则化偏移.

3 无记忆牛顿-模拟退火法 3.1 大规模无约束最优化问题

对求解无约束最优化问题(4)的方法有不同的分类方法.若从求解过程中是否需要计算目标函数的导数划分，可以简明地分为直接法和非直接法[18].直接法，即无需计算目标函数导数值的方法.对于正则化偏移中的最优化问题，导数往往难以计算，即使其导数可以计算，计算量也会异常巨大.而直接法能免去计算目标函数的导数，因此近年来该类方法受到越来越多的重视[14].能避免导数计算会给问题的求解带来方便，但同时却会给对该方法的分析带来困难.因为缺乏导数的计算，我们较难对其性质进行理论分析，这又成为进一步发展的瓶颈.非直接法，即在求解过程中需要计算目标函数导数的方法.很多实验表明，在仅利用一阶导数的方法中，拟牛顿法(也称变尺度法)是最为有效的一种方法.这个方向的研究已经相当成熟，甚至有学者认为，要在拟牛顿法中找到比BGFS方法好得多的方法已经不大可能[18].除此之外，共轭梯度法也是非直接方法求解反演问题中很重要的一种方法[1， 13]，它具有二次终止性，简单可靠等优点，但对一般的非凸函数问题收敛速度较慢.在它的基础上能作很多改进，例如无记忆拟牛顿法､预条件共轭梯度法等等.

从搜索的思路来看，又可分为非启发式搜索(盲目搜索)和启发式搜索.非启发式搜索是按预定的控制策略进行，在搜索的过程中所获得的信息不被用来改进控制策略的一种搜索.非启发式反演并不利用能够求得全局最优解的启发性知识.上文所述的不少数值最优化方法都属于这种类型.此类方法一般只能求得问题的一个稳定点或K-T 点，不能保证求得问题的全局最优解，在目标函数存在多个极值点的情况下有可能陷入局部极值.而启发式搜索则在搜索中加入了与问题有关的启发式信息，用来指导搜索朝着最有希望的方向前进，加速问题的求解过程，并找到全局最优解.近年来对它的研究如火如荼，具有代表性的方法有模拟退火法，遗传算法，量子退火法，蚁群算法，神经网络算法等等.此类方法一般可保证得到全局最优解，但是计算量巨大，而且各种方法都有各自的问题.例如:模拟退火法中温度参数不好确定，遗传算法中反演参数不能太多，等等.

3.2 无记忆拟牛顿-模拟退火法

目前求解无约束最优正则化问题(4)流行使用拟牛顿法或共轭梯度法求解.但对于超大规模的最优化问题，拟牛顿法通常需要更大的内存，所以本文考虑使用在共轭梯度法基础上改进的方法来作为求解最优化问题的方法.共轭梯度法具有二次终止性，内存需要量小，但是对于非凸函数它的收敛速度往往退化为线性速度.无记忆拟牛顿法是对共轭梯度法的一种改进，在每一步迭代要求逼近求解函数f(m)的二阶校正项▽2f(m)，即

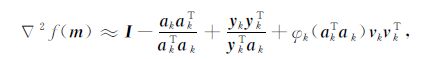
其中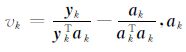，为搜索步长，yk为当前梯度值与上一步梯度值的余量差，φk为取0或1的正参数，I为单位矩阵.该方法无论在内存还是每次迭代的计算量上都与共轭梯度法相差无几，而它的计算表现比共轭梯度法要好得多[18].由于以上这些非启发式方法对于多极值的目标函数均不能保证得到全局最优解，而地震偏移成像中的无约束最优正则化问题(4)有可能出现多极值的情况，因此本文考虑加入模拟退火法混合使用，帮助其跳出局部最优解.模拟退火法(SA)能得到全局最优解，但是它具有一定的概率性质的存在使得求解的结果有一定的不合理性，另外退火过程的计算量也很大.本文把无记忆拟牛顿法(MQN)和模拟退火法(SA)各自的优点恰当地组合起来，形成了MQN-SA 算法.数值实验表明，该方法能跳出用无记忆拟牛顿法得到的局部最优解，从而提高了全局收敛性；并且所得到的全局最优解必然是合理的，而不会像用模拟退火法得到的最优解那样只是有较大概率是合理的.下面给出MQN-SA 算法.

算法1(MQN-SA)

步骤1 设置冷却表参数.任给初始温度T0 和初始解m0，设置外循环迭代次数outn, 内循环马可夫链长度inn, 温度衰减系数dec, 设定模型参数的变化范围a，以及最低温度(截止温度)tmin, i=0；

步骤2 利用MQN 方法，求得当前最优解mi，然后计算f(mi)，并把这两个结果保存起来.然后进入下一层循环，令k=0，tk=T0 及比例因子b=0；

步骤3 若此时tk＜tmin, 则转入步骤6；否则令mk= mi，然后得到mk+1 = mk+ξka，其中ξk=tk*sign(r-0.5)*[(1-1/tk)|2r-1|-1，r为[0,1]之间服从均匀分布的随机数.计算相应的目标函数值的差值ΔE=f(mk+1)-f(mk)；

步骤4 若ΔE≤ 0，则令mk+1 = mk；否则若e(-ΔE/tk)>r，则mk+1 =mk；重复步骤3直到k=inn转入步骤5；

步骤5 缓慢降低温度tk，令tk+1 =tk*(dec)b，模仿降温退火过程.再令b=b+1，k=k+1，转步骤3；

步骤6 令i=i+1，如果i＜outn, 转到步骤2；否则比较保存的所有outn个近似最优解所计算出的函数值，取最小值所对应的解即为所求得全局最优化的解，也即地震正演算子方程的解.

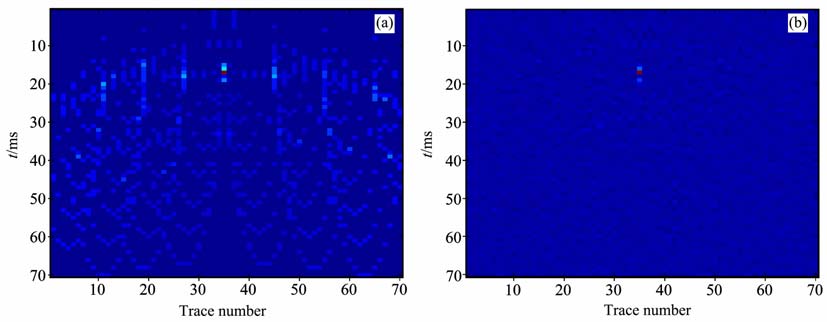
4 数值模拟与结果分析 4.1 单点绕射模型

假设检波器分布在一条长1000 m 的直线上，道间距20m, 时间采样率为2 ms.地下背景速度均匀，均为4000m/s, 仅有一个速度异常点，其速度为2500m/s.由于实际地震数据不可避免地带有误差，因此我们对本文中的几个人工合成地震数据都加入一个随机白噪声.本实验中，添加噪音水平为0.01.实验中取301×51的网格，也即水平采样间隔为dx=40m, 垂直采样间隔为dz= 8 m.假设速度异常点在水平正中埋深为600m 处.Kirchhoff叠后时间偏移的结果和利用了MQN-SA 技术的正则化偏移的结果分别见图 1a和图 1b.容易看出，图 1a中有明显的划弧现象，而图 1b中去除了划弧现象，并且成像点相对能量更强，成像更清晰.深入计算结果分析，发现Kirchhoff叠后时间偏移算出成像点的反射系数为0.006，这完全是假象，不能为后续的岩性分析或精细解释提供准确的信息；而MQN-SA 正则化偏移算出的则是0.296，很接近真实的反射系数值0.231，有很好的实用价值.

图 1 Kirchhoff偏移(a)和MQN-SA正则化偏移(b) Fig. 1 Kirchhoff migration (a) and MQN-SA regularized migration (b)
4.2 多层模型

为了进一步验证算法的可靠性，设计一个5层的速度模型，包含倾斜反射层，其中第三､第四个反射界面的倾角分别为21.8°和45°，各层的层速度见表 1.

表 1 速度模型各层的层速度 Table 1 Velocity for layers in the velocity model

假设各层密度一致，由上表可得到真实的反射系数模型如图 2.

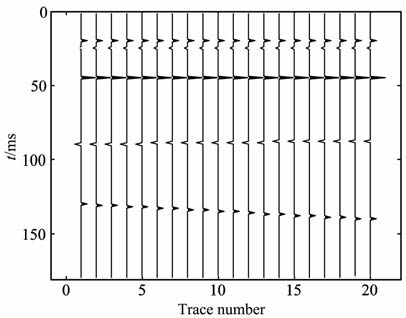
图 2 真实反射系数模型 Fig. 2 The real reflectivity model

此实验中，添加噪音水平为0.01.Kirchhoff叠后时间偏移的结果和MQN-SA 正则化偏移的结果分别见图 3a和图 3b.MQN-SA 正则化偏移后的图像比Kirchhoff叠后时间偏移得到的图像在子波振荡的压制方面有明显的改善.图 3a中子波旁瓣较宽，且在很多地方噪音有所放大.

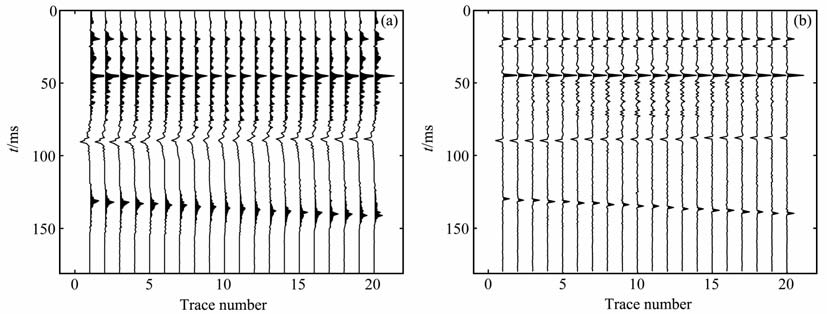
图 3 噪音水平0.01的Kirchhoff偏移(a)和MQN-SA正则化偏移(b) Fig. 3 Kirchhoff migration (a) and MQN-SA regularized migration (b)
4.3 断层模型

以下对断层这一常见的构造类型测试算法的有效性.模型中三个地层的速度从上到下分别为2000m/s, 2500m/s和3000 m/s.取101×101 的网格，水平采样间隔为dx=40 m, 时间采样率为dt= 0.002s.本实验中，添加噪音水平为0.1.图 4a和图 4b分别是Kirchhoff叠后时间偏移的结果和MQN-SA 正则化偏移的结果.可以看出Kirchhoff叠后时间偏移给出的是一个模糊的图像，而后者则相当清晰.

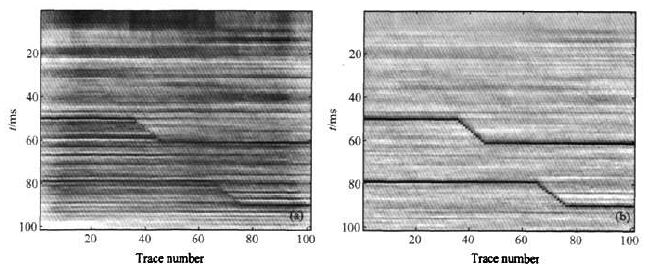
图 4 噪音水平0.1的Kirchhoff偏移(a)和MQN-SA正则化偏移(b) Fig. 4 Kirchhoff migration (a) and MQN-SA regularized migration (b)
4.4 真实数据测试

图 5是某油田的一个地震水平叠加剖面，为了展示方便，抽取了其中的10道数据，每道有401个时间采样点，时间采样率为0.004s.

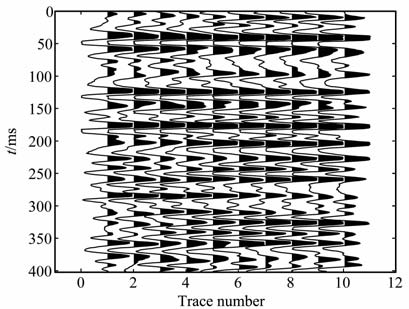
图 5 真实数据叠加剖面 Fig. 5 The stack section for field data

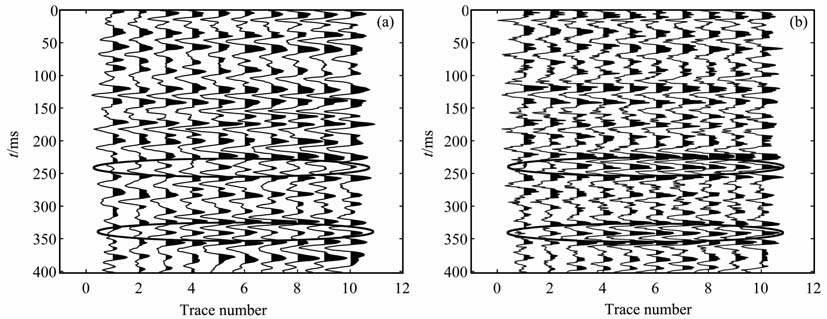
Kirchhoff叠后时间偏移的结果和MQN-SA 正则化偏移的结果分别见图 6a和图 6b，从两个目标层位的成像对比(黑圈区域)可见MQN-SA 正则化偏移的分辨率更高.然后，对输出剖面每点的振幅值进行分析，把图 6a与图 6b对应位置的振幅值相减，作差得到图的显示效果与图 6a几乎一致，这是因为图 6a中的振幅值都严重失真，比图 6b的都大数百倍，因此所减去的值几乎可以忽略.由此可知，只有图 6b的反射系数才可能具有真实的地质意义，能作后续分析的使用，图 6a仅能提供一个构造位置大致正确的图像，其每点上的振幅已经严重失真.

图 6 Kirchhoff偏移(a)和MQN-SA正则化偏移(b) Fig. 6 Kirchhoff migration (a) and MQN-SA regularized migration (b)
4.5 性能分析

本文提出的新算法比Kirchhoff偏移的效果要好，储存量需求相当，但计算速度会变慢，表 2 给出两种方法在计算耗时上的对比.

表 2 Kirchhof偏移与MQN-SA偏移的性能对比 Table 2 Performance analysis for Kirchhoff migration and MQN-SA migration
5 结语

正则化偏移是一个值得探索的领域，优良的反演算法在这个领域有广阔的应用空间.本文基于正则化偏移的数学模型，提出了一种混合的迭代反演算法，可以找到全局最优解，并且在局部寻优中具有精度高，抗病态能力强，收敛速度较快等优点.使算法适应各种地震正演模型，利用预条件子改善正演矩阵的性质，是未来进一步改善的方向.该方法比工业界广泛应用的Kirchhoff偏移多花费至少一个数量级的时间，但是通过并行算法设计，运算时间存在大量减少的可能，并且我们还可以只对感兴趣的区域(例如，薄层)使用该方法进行偏移，这样计算量也将大幅减少.

参考文献
[1] 王彦飞. 反演问题的计算方法及其应用. 北京:高等教育出版社. 2007 . Wang Y F. Computational Methods for Inverse Problem and Their Applications (New Frontiers of Sciences) (in Chinese). Beijing: Higher Education Press, 2007 .
[2] Bleistein N. Mathematics of Multidimensional Seismic Imaging, Migration, and Inversion. Springer, 2000
[3] 马在田. 论反射地震偏移成像. 勘探地球物理进展 , 2002, 25(3): 631–635. Ma Z T. On reflection seismic migration imaging. Progress in Exploration Geophysics (in Chinese) , 2002, 25(3): 631-635.
[4] Nemeth T, Wu C J, G T Schuster. Least-squares migration of incomplete reflection data. Geophysics , 1999, 64(1): 208-221. DOI:10.1190/1.1444517
[5] Sacchi M D, Wang J F, H Kuehl. Regularized migration/inversion: New Generation of Seismic Imaging Algorithm. CSEG RECORDER, 2006 Special Edition. 54~59
[6] 肖庭延, 于慎根, 王彦飞. 反问题的数值解法. 北京: 科学出版社, 2003 . Xiao T Y, Yu S G, Wang Y F. Numerical Solution for Inverse Problem (in Chinese). Beijing: Science Press, 2003 .
[7] Claerbout J F. Earth soundings analysis: Processing versus inversion. Blackwell Scientific Publications, Inc, 1992
[8] Fessler J A, Booth S D. Conjugate-Gradient Preconditioning Methods for Shift-Variant PET Image Reconstruction. IEEE Transactions on Image Processing , 1999, 8(5): 52-62.
[9] Hu J X, G T Schuster, P A Valasek. Poststack migration deconvolution. Geophysics , 2001, 66(3): 939-952. DOI:10.1190/1.1444984
[10] Yu J H, Hu J X, G T Schuster, et al. Prestack migration deconvolution. Geophysics , 2006, 71(2): 53.
[11] Lecomte I, Gelius L J. Have a look at the resolution of prestack depth migration for any model, survey and wavefields. SEG Expanded Abstacts , 1998, 17: 1112.
[12] Gelius L J, Lecomte I, Tabti H. Analysis of the resolution function in seismic prestack depth imaging. Geophysical Prospecting , 2002, 50: 505-515. DOI:10.1046/j.1365-2478.2002.00331.x
[13] 王彦飞, 杨长春, 段秋梁. 地震偏移反演成像的迭代正则化方法研究. 地球物理学报 , 2009, 52(6): 1615–1624. Wang Y F, Yang C C, Duan Q L. On iterative regularization methods for migration deconvolution and inversion in seismic imaging. Chinese J. Geophys. (in Chinese) , 2009, 52(6): 1615-1624.
[14] Wang Y F, Yang C C. Accelerating migration deconvolution using a non-monotone gradient method. Geophysics , 2010, 75(4): 131-137. DOI:10.1190/1.3457923
[15] Stolt R H, Benson A K. Seismic Migration: Theory and Pratice, Vol. 5, Handbook of Geophysical Exploration, Section I, Seismic Exploration. London: Geophysical Press, 1986
[16] Yilmaz O. Seismic Data Processing, Investigations in Geophysics No. 2. Society of Exploration Geophysicists, Tulsa, Okla, 1987
[17] 陆基孟. 地震勘探原理. 东营: 石油大学出版社, 1993 . Lu J M. Principle of seismic exploration (in Chinese). Dongying: Petroleum University Press, 1993 .
[18] 袁亚湘. 非线性规划数值方法. 上海: 上海科学与技术出版社, 1993 . Yuan Y X. Numerical Methods for Nonlinear Programming (in Chinese). Shanghai: Shanghai Scientific and Technical Publishers, 1993 .