地球物理学报  2011, Vol. 54 Issue (3): 787-792   PDF    
引用本文
卞光浪, 翟国君, 刘雁春 等. 基于Laplace法的磁性球体参数确定. 地球物理学报, 2011, 54(3): 787-792, doi: 10.3969/j.issn.0001-5733.2011.03.019.  
BIAN G L, ZHAI G J, LIU Y C, et al. The parameters determination of magnetic spherical object based on Laplace approach. Chinese J. Geophys. (in Chinese), 2011, 54(3): 787-792, doi: 10.3969/j.issn.0001-5733.2011.03.019.  
基于Laplace法的磁性球体参数确定
卞光浪1,2 , 翟国君2 , 刘雁春1 , 黄谟涛2     
1. 海军大连舰艇学院海测工程系,大连 116018;
2. 海军海洋测绘研究所,天津 300061
收稿日期 2010-06-10, 2011-01-05 收修定稿
基金项目: 国家自然科学基金(40671161)资助.
作者简介: 卞光浪,男,1984年生,博士生,主要从事海洋磁力测量理论与数据处理研究.E-mail:jsbgl@163.com
摘要: 解析信号法被广泛应用于磁性目标平面位置确定中,然而,数值计算表明:斜磁化情况下,解析信号模极大值与磁性目标中心平面位置之间存在较大的偏差,最大可达探测深度的30%,从而制约了该方法在航空磁测或水深较深区域的应用.从理论上推导了磁性球体磁异常经拉普拉斯算子运算后信号(简称"拉普拉斯信号")表达式,分析了其具有的物理性质,在此基础上,提出采用Laplace法确定磁性目标中心平面位置,当地磁场与磁化强度倾角相同且大于30°时,仿真计算的磁性球体平面位置误差小于深度的4.3%,大大提高了平面位置的计算精度.此外,还给出了磁性目标的深度和磁性参数的计算方法.仿真结果表明,当磁性球体空间位置确定较为准确时,计算出的磁性球体空间位置与磁性参数和实际值较为相符.
关键词: 磁性目标探测      Laplace法      解析信号法      球体模型     
The parameters determination of magnetic spherical object based on Laplace approach
BIAN Guang-Lang1,2, ZHAI Guo-Jun2, LIU Yan-Chun1, HUANG Mo-Tao2     
1. Department of Hydrography and Cartography, Dalian Naval Academy, Dalian 116018, China;
2. Naval Institute of Hydrographic Surveying and Charting, Tianjin 300061, China
Abstract: Analytic signal approach is widely applied in obtaining source locations through the maxima of the amplitude of the analytic signal (AAS). However, the maximum value of the AAS for a sphere model does not coincide with the object epicenter exactly. The error in the horizontal location increases with the object depth, reaching a maximum of 30% of the depth. Thus, the approach is not suitable for the condition of airborne detection or deep depth. The Laplacian signal expression of magnetic sphere magnetic anomaly was deduced theoretically. Based on its characteristic, Laplace approach is proposed to locate the magnetic object, and its horizontal location error calculated by simulation is less than 4.3% of the depth when the inclination is more than 30°, having the evident advantage over AAS approach. The depth and magnetism parameters calculating methods have also been brought forward, and simulation example indicates that calculated result and real value matches perfectly if exact spatial position is known..
Key words: Magnetic object detection      Laplace approach      AAS approach      Sphere model     
1 引言

磁探测技术能快速､有效地探测水下小尺度磁性目标，在沉船､水雷､海底电缆和水下潜航器探测方面得到了较为广泛的应用[1， 2].该技术的基本原理是根据磁性目标周围的磁场信息，通过一定的数学解释手段，判断磁性目标的空间位置､大小､形状和磁性参数，在磁力勘探中，称为磁异常反演.目前，普遍应用的磁性目标空间位置定量计算方法主要有解析信号法(AAS)和Euler法等[3].解析信号法[4]认为总强度磁异常经过该方法变换后的极值受磁化强度方向影响较小，对应于磁性目标的中心位置.Euler法[5~8]从数学角度出发，以欧拉齐次方程为基础，推断磁性目标中心的空间位置.然而，笔者通过球体磁场模型计算表明:解析信号法计算的磁性目标中心平面位置与真实值存在较大的偏差，最大可达探测深度的30%.显然，这样的平面位置定位精度很难满足航空磁测或深水区域的磁探测要求.Euler法反演解的发散性､复杂形体构造指数的不确定性以及深度解算的不稳定性，在一定程度上也影响了其在工程实践中的应用[9].

磁通门式磁力仪和超导量子磁力仪能同时测量磁场三分量[10， 11]，获取的信息能更全面地反映磁性目标的磁场特征.随着这类分量磁力仪的逐渐应用，有必要研究利用磁场分量自动解算磁性目标参数的方法.本文以小尺度磁性球体为研究对象，提出Laplace法求解磁性球体中心的平面位置.在磁性球体深度计算方面，Salem 等[12]提出利用垂直分量一阶导数和二阶导数信号模比值方法(简称为“比值法")，这种方法需要求解垂直分量的二阶导数，受噪声影响较大，同时，深度计算精度直接与平面位置的准确程度有关.如果解析信号法确定目标平面位置存在较大偏差，最终也会将这种误差传递给深度计算结果，降低深度计算精度.为此，提出一种新的深度解算方法，该方法只需要求解分量的一阶导数，可以降低噪声对深度解算结果的影响.此外，还给出了磁性参数的求解方法，为识别磁性目标提供重要依据.现阶段，我国海洋磁力测量普查和勘探中，以测量总场强度为主，此时，可以采用频域换算方法获得磁异常的三分量及分量导数[13]，再利用Laplace法求解磁性目标中心的平面位置，并进一步计算磁性目标深度及磁性参数.仿真试验验证了提出方法的可行性.

2 ΔBT 形式及物理性质

Laplace算子(Δ= ▽2)求解的是磁场空间变化率的变化率，能突出反映空间磁场畸变的位置，通过对磁性目标磁异常强度BT 的Laplace算子运算(称为“拉普拉斯信号")，其极值位置能很好地对应磁性目标中心平面位置.下面以球体磁场为例，推导BT经Laplace算子运算后的形式及其物理性质.

在笛卡儿右手空间直角坐标系中，磁性球体的中心位置为O(x0，y0，z0)，矢量磁矩为m= mxi+myj+mzk，球体中心至测点P(x，y，z)距离矢量为r=rxi+ryj+rzk.以Bx､By和Bz表示磁性球体引起的磁异常强度BT 在x方向､y方向与z方向的磁异常分量，有如下各式成立[14]:

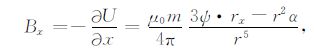
(1)

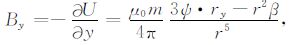
(2)

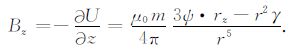
(3)

式中，

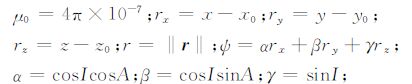
I与A分别为磁化强度倾角及偏角，U为磁性球体的磁位，m= ‖m‖ 为磁矩模.

磁异常强度BT 是Bx､By和Bz的均方根，可表示为

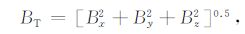
(4)

对BT 进行Laplace算子运算后得

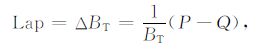
(5)

式中，

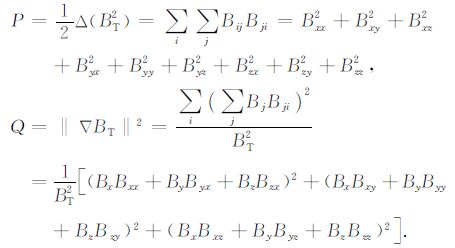
公式(5)中Bij(i，j=x，y，z)表示Bi分量在j方向的偏导数，其通式为[15]

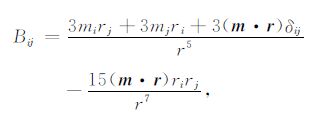
(6)

其中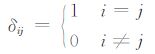，，为了简化符号运算，(6)式中将μ0/4π合并入m(下同).

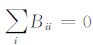
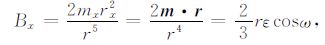
根据Maxwell方程，在磁性目标外部无源空间，磁异常B的散度和旋度为零[16]，存在关系式:Bij=Bji(对称性)，(无迹性)，可见，Bij中仅有5个元素独立.由于(5)式中包含项数较多，且形式复杂，难以直观看出BT 经Laplace算子运算后的极值与磁性球体中心平面位置间相互联系.根据BT 经Laplace算子运算后为标量，具有旋转不变性的特点[16]，即拉普拉斯信号与坐标系的选取无关，建立如下笛卡儿空间直角坐标系:以球体中心为坐标原点，x轴由球体中心指向测点，y轴位于包含m与r的平面内，z轴平行于m×r.设ω 为m与r间夹角，由x偏向y方向为正值，则存在关系式:rx=r，ry=0，rz=0，mx=mcosω，my=msinω，mz=0，将这些关系式代入(1)~ (3)式和(6)式，并令ε =3m/r4，得

(7)

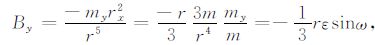
(8)

(9)

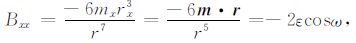
(10)

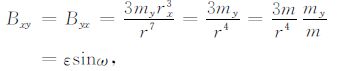
(11)

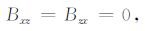
(12)

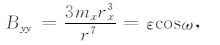
(13)

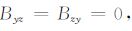
(14)

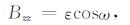
(15)

将(7)~(15)式代入(5)式，经整理后得

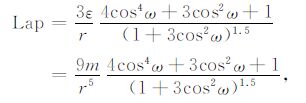
(16)

故有

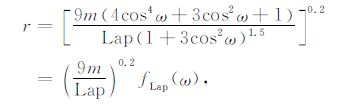
(17)

式中，.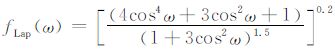

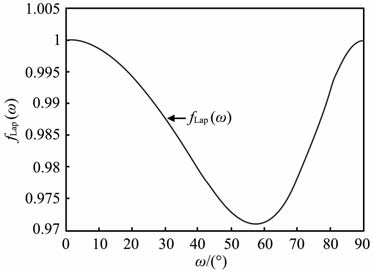
当固定m和Lap时，(17)式就表示拉普拉斯信号等值面上测点与球体中心距离，可见，等值面的形状与fLap(ω)有关，如果fLap(ω)=1，表明等值面为球面，则在任意观测平面上，磁性目标中心在观测平面上投影点均对应该平面上信号的最大值.特殊地，如果观测面为水平面，拉普拉斯信号极大值就对应磁性目标中心的平面位置.图 1为ω∈ [0°，90°]时，fLap(ω)随ω 的变化规律.

图 1 fLap (ω)与ω变化关系 Fig. 1 The relationship between fLap (ω) and ω

从图 1可以看出，在ω ∈ [0°，90°]内，fLap(ω)值先减小后增大，但始终非常接近于1，其最大值为fLap(0.0°)=fLap(90.0°)=1，最小值为fLap(57.6°)=0.971，最大值与最小值之比为1.03∶1，表明BT 经Laplace算子运算后的等值面极其接近于球面.所以，当观测面为水平面时，观测面上拉普拉斯信号极大值对应磁性目标中心的平面位置.

由实际情况知，不同观测高度对平面定位精度要求是有差异的，例如，船载磁力测量时，观测平面距离磁性目标较近，获取的磁性目标磁场信息相对完整，因而磁性目标的平面位置计算精度较高；相反，利用航空磁力测量时，观测平面距离磁性目标较远，获取的信息不完整，则应该适当放宽平面定位精度.所以，仅凭点位误差无法全面､客观地反映定位方法的优劣，为此，采用平面位置的点位误差和深度之比作为精度评定指标，公式如(18)所示.

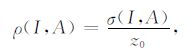
(18)

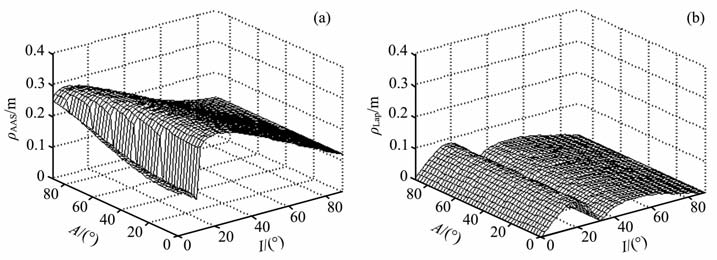
式中，ρ(I，A)表示计算的平面位置点位误差和深度之比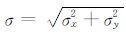；为点位误差，σx和σy分别为x､y方向误差.

为定量分析Laplace法确定的磁性目标中心平面位置精度，采用球体磁场数值模拟方法进行说明，并与常用的解析信号法计算结果进行对比.图 2 是不同磁化强度偏角和倾角情况下，解析信号法和Laplace法确定的平面位置点位误差和深度之比.

图 2 不同倾角与偏角情况下解析信号法和Laplace法计算的球体平面位置点位误差与深度之比 球体深度和磁矩分别为20 m与5654.87 A • m2，地磁场倾角和偏角分别为50°与5°.(a) ρAAS； (b) ρLap Fig. 2 ρ(I,A) of the analytic signal and Laplace signal of a dipole source with different magnetization direction The depth and magnetic moment of the sphere model is 20 m and 5654.87 A • m2 respectively； the normal field has declination 5° and inclination 50°.

由图 2可以看出，在磁性球体中心平面位置计算中，磁偏角变化对两种方法的计算精度影响较小，而磁倾角的影响相对较大.经计算，利用解析信号法计算的最大值为ρAAS(18°，46°)=30.02%，最小值为ρAAS(10°，20°)=9.71%，平均值达21.09%；而利用Laplace法计算的最大值为ρLap(10°，16°)=8.75%，平均值为3.68%，在I=0°和90°时，平面位置无误差.我国周边海区的地磁场倾角一般大于30°，当磁化强度倾角与地磁场倾角较为接近时，利用Laplace法计算出的平面位置点位误差和深度之比则不超过4.30%，即观测高度为100 m 时，平面位置误差小于4.3m, 可以满足工程测量的需求.

3 垂直深度及磁性参数确定 3.1 垂直深度确定

由(1)~(3)式，磁性球体中心在xoy平面上投影点为(x0，y0，0)，该点处的磁场分量分别为

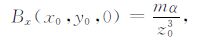
(19)

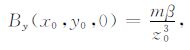
(20)

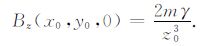
(21)

将(19)~(21)式分别代入BT 和‖▽BT‖表达式得

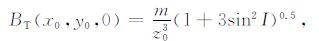
(22)

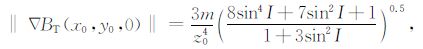
(23)

将(22)式与(23)式两端分别相除，整理后得磁性球体的深度:

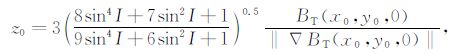
(24)

令,.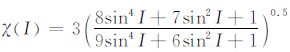

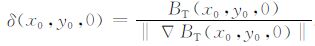
由极值条件可知，在I∈[0°，90°]内，χ(I)在I=0°和90°时取最小值，χ(0°)=3 与χ(90°)=3；在I=24.1°时取最大值，χ(24.1°)=3.09.由此可见，χ(I)在[0°，90°]变化很小，近似为常值.本文仿真分析中取χ(I)=3，则z0=3δ(x0，y0，0).

3.2 磁性参数确定

根据(19)~(22)式，还可进一步得到磁偏角､磁倾角和磁矩参数表达式:

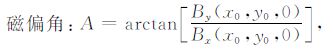
(25)

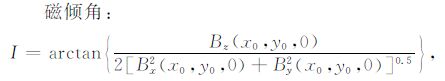
(26)

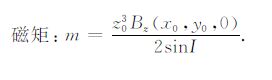
(27)

4 仿真计算与分析

为说明提出的磁性目标空间位置和磁性参数确定方法的有效性，下面采用磁异常仿真数据进行分析.

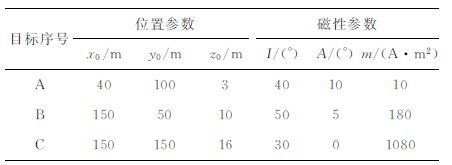
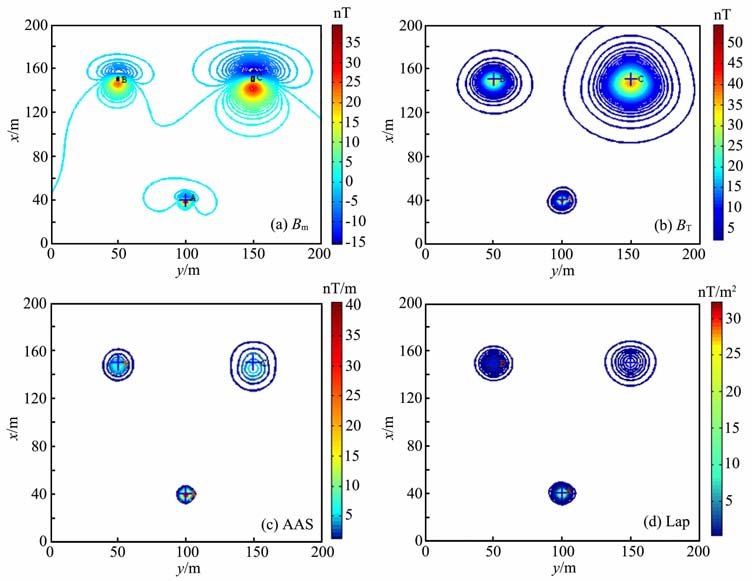
设地磁场倾角和偏角分别为I0 =50°与A0 =5°，仿真的测区面积为200 m×200 m, 测线和测点间距均为5m.采用球体磁场与长方体无解析奇点磁场表达式[17]仿真了球体和长方体磁异常，球体与长方体模型相关参数如表 1所示，其中A 为球体，B和C 为长方体，长､宽､高分别为3m×1m×2m 与4m×2 m×3 m.仿真得到磁性目标在平面上的总强度磁异常Bm､磁异常强度BT､解析信号值AAS和拉普拉斯信号Lap等值线所图 3 所示，图中“□"和“+"分别表示长方体边界与球体中心平面位置.

表 1 仿真磁性目标参数 Table 1 Parameters of simulated model
图 3 仿真磁性目标的Bm(a)､BT(b)､AAS (c)和Lap (d)等值线图 Fig. 3 Contour map of (a) Bm､BT(b)､BT(c) AAS and (d) Lap of simulation sphere model

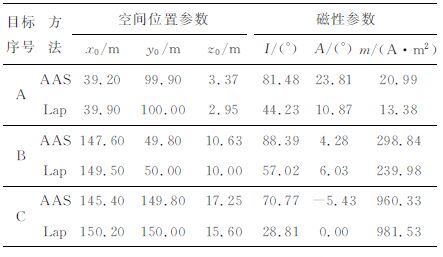
由图 3可以看出，解析信号法极大值位置与磁性目标中心位置在x方向上明显存在一定的偏移，而拉普拉斯信号极大值位置能很好地对应磁性目标的中心位置.由于磁探测中获取的数据为离散数据，计算的拉普拉斯信号极大值位于磁性目标附近的格网点上，如果格网间距过大，得到的平面位置误差有可能较大，此时，可将离散的拉普拉斯信号数据进行更高分辨率的格网化，具体可视磁性目标的形体大小和探测精度而定；当测区范围较大时，也可对局部测区进行高分辨率的格网化处理.本文采用Kriging格网化法，格网化后分辨率为0.1 m×0.1 m, 计算出的磁性目标空间位置和磁性参数如表 2 所示，表中还列出了综合解析信号法和比值法计算的磁性目标空间位置结果，而磁性参数采用(25)~(27)式计算，统称为解析信号法(简记为“AAS法").

表 2 解析信号法和Laplace法计算得到的球体参数 Table 2 Model parameters estimations with analytic signal and Laplace approach

由表 2，Laplace法平面位置计算精度显著优于解析信号法计算精度，解析信号法在x方向和y方向的最大值分别为4.6m 与0.2m, 而Laplace法在x方向和y方向误差最大值仅为0.5m与0m, 造成两个方向上位置误差存在差异的原因是:仿真试验中采用的地磁场与磁化强度偏角均小于10°，偏向x方向一侧.在深度和磁性参数计算中，解析信号法受平面位置较大误差的影响，其计算结果精度也均明显低于Laplace法计算精度，特别是磁性参数，解析信号法计算出的结果基本无法反映真实值，而Laplace法计算出的结果与实际值较为接近.

5 结论

(1) 建立了一种特殊坐标系，从理论上推导了基于磁异常强度的拉普拉斯信号表达式，通过数值模拟表明，拉普拉斯信号等值面非常接近于球面，等值面上距离球体中心最远测点和最近测点之比仅为1.03∶1，因此，水平面上拉普拉斯信号极大值能很好地对应磁性目标中心平面位置.

(2) 提出的深度计算方法受平面位置定位误差影响较小，结合Laplace法较高的磁性目标平面位置计算精度，深度计算结果具有较强的稳定性.同时，深度计算法只需求解磁场分量的一阶导数，较比值法而言，降低了噪声对计算结果的影响.根据磁场分量间相互关系，进一步给出了磁性参数求解方法，仿真试验表明:磁性参数计算结果与实际磁性参数值较为接近.

(3) 本文研究成果对于研制张量梯度测量系统具有一定的借鉴意义.张量梯度模是目前小尺度磁性目标探测中的热点研究内容，利用拉普拉斯信号类似的推导步骤可得到张量梯度模表达式，进而分析其具有的一些物理性质.

致谢

感谢两位匿名评审专家提出的宝贵修改意见.

参考文献
[1] Dwain K, Butler. Implications of magnetic backgrounds for unexploded ordnance detection. Journal of Applied Geophysics , 2003, 54: 111-125. DOI:10.1016/j.jappgeo.2003.08.022
[2] 郭志宏.航磁及梯度数据正反演解释方法技术实用化改进及应用. 北京:中国地质大学,2004. Guo Z H. The practical improvement of forward and inversion technique on aeromagnetic gradient data and its application (in Chinese). Beijing: China University of Geosciences,2004
[3] Salem A, Ravat D. A combined analytic signal and Euler method (AN-EUL) for automatic interpretation of magnetic data. Geophysics , 2003, 68: 1952-1961. DOI:10.1190/1.1635049
[4] Salem A, Ravat D, Gamey J. Analytic signal approach and its applicability in environmental magnetic investigations. Journal of Applied Geophysics , 2002, 49: 231-244. DOI:10.1016/S0926-9851(02)00125-8
[5] Wen B D, Hsu S K, Yi C Y. A derivative-based interpretation approach to estimating source parameters of simple 2D magnetic sources from Euler deconvolution, the analytic-signal method and analytical expressions of the anomalies. Geophysical Prospecting , 2007, 55: 255-264. DOI:10.1111/gpr.2007.55.issue-2
[6] Geralda D F, Reidb A, McInerney P. New discrimination techniques for Euler deconvolution. Computers & Geosciences , 2004, 30(2): 461-469.
[7] Gerovskaa D, Marcos J, Araúzo B. Automatic interpretation of magnetic data based on Euler deconvolution with unprescribed structural index. Computers & Geosciences , 2003, 29: 949-960.
[8] Keating P, Pilkington M. Euler deconvolution of the analytic signal and its application to magnetic interpretation. Geophysical Prospecting , 2004, 52: 165-182. DOI:10.1111/gpr.2004.52.issue-3
[9] 范美宁.欧拉反褶积方法的研究及应用.长春:吉林大学,2006. Fan M N. The study and application of Euler deconvolution method (in Chinese). Changchun: Jilin University,2006
[10] 刘士杰, 卢军, 高林征, 等. 三分量磁饱和式磁力仪. 地球物理学报 , 1980, 23(3): 298–305. Liu S J, Lu J, Gao L Z, et al. A three component flux-gate magnetometer. Chinese J. Geophys. (in Chinese) , 1980, 23(3): 298-305.
[11] 田永君, 王天生, 陈珂, 等. 用于无屏蔽环境生物磁测量的倒装片式高温超导梯度计. 中国科学(A辑) , 1999, 29(12): 1119–1124. Tian Y J, Wang T S, Chen K, et al. Hyperbatic high temperature superconducting quantum interference devices for unshielded environment biology survey. Science in China (Series A) (in Chinese) , 1999, 29(12): 1119-1124.
[12] Salem A, Hamada T, Asahina T H, et al. Detection of unexploded ordnance (UXO) using marine magnetic gradiometer data. Exploration Geophysics , 2005, 58(1): 97-103.
[13] Blakely R J. Potential Theory in Gravity and Magnetic Applications. Cambridge:Cambridge University Press,1995
[14] 管志宁. 地磁场与磁力勘探. 北京: 地质出版社, 2005 . Guan Z N. Magnetic Field and Magnetic Exploration (in Chinese). Beijing: Geological Publishing House, 2005 .
[15] Wiegert R F. Magnetic anomaly sensing system for detection, localization and classification of magnetic objects.US Patent,US6841994B1,2005-1-11
[16] 张昌达. 航空磁力梯度张量测量——航空磁测技术的最新进展. 工程地球物理学报 , 2006, 3(5): 354–361. Zhang C D. Airborne tensor magnetic gradiometry-the latest progress of airborne magnetometric technology. Chinese Journal of Engineering Geophysics (in Chinese) , 2006, 3(5): 354-361.
[17] Schmidt P W, Clark D A. The magnetic gradient tensor: its properties and uses in source characterization. The Leading Edge , 2006, 25(1): 75-78. DOI:10.1190/1.2164759
[18] 郭志宏, 管志宁, 熊盛青. 长方体ΔT场及其梯度场无解析奇点理论表达式. 地球物理学报 , 2004, 47(6): 1131–1138. Guo Z H, Guan Z N, Xiong S Q. Cuboid ΔT and its gradient forward theoretical expressions without analytic odd points. Chinese J. Geophys. (in Chinese) , 2004, 47(6): 1131-1138.