2. 第二炮兵工程学院,西安 710025
2. Xi'an Research Institute of High Technology, Xi'an 710025,China
地球变化磁场可分为规则变化与不规则变化,K指数作为最常用的一种地磁活动指数,它描述的是不规则变化的剧烈程度.因此,规则变化也称作非K变化(non-Kvariations),而将不规则变化称为K变化(Kvariations)[1].非K变化主要包括太阳静日变化Sq和太阴日变化L,其中Sq占主导地位,L的幅度很小.消去非K变化,得到的就是K变化;K指数以3h为一时段,用0,1,…,9分10级来表示其扰动程度.
经过几十年的发展和实践,K指数作为一种重要的地磁活动指数,已经在世界范围内得到认可,K指数的计算也成为地磁台站的重要工作之一.然而,追溯到1939年,再次审视Bartels等人设计K指数的基本思想,我们又不得不指出K指数的一些不足之处.K指数的标定通常采用水平方向的两个分量X(或H)和Y(或D):先分别标定两个分量各自的K指数,再取其大者作为最终的K指数.以扰动大的分量决定K指数,似乎并无不妥之处,而事实却并非如此,Reda等[2]对此便提出了疑义,他们发现:
(1) K指数由地磁分量的最大扰动幅度来决定是不合理的,因为地磁场的扰动不仅仅表现在地磁分量的扰动幅度,还表现在地磁场矢量方向的变化上.因此,如果仅仅以分量的扰动幅度来决定K指数,那么K指数的标定往往依赖于坐标系的选取---用X和Y两分量确定的K指数与用H和D两分量确定的K指数是不同的,这种差异在磁偏角较大的台站尤为明显(误差最大可达30%);
(2) K指数的确定与3小时段内不规则扰动的次数无关,这就导致发生一次不规则扰动与发生多次同等程度的不规则扰动所对应的K指数相同;
(3) K指数的标定取决于扰动最大的分量,这就使得KX=3且KY=0 与KX=3 且KY=3 这两种不同的扰动程度对应的K指数相同(KX表示以X分量标定的K指数,KY表示以Y分量标定的K指数).
我国基本处于磁纬40°以下地区,H分量扰动最为剧烈[3~7],通常使用H分量来标定K指数,因此,国内地磁台站标定的K指数也同样存在上述的缺陷.另外,文献[8],[9]对K指数也提出疑义.
地磁场的扰动,归因于日地能量的耦合,它反映的是地磁场各分量所包含的能量的变化.然而,能量本身是看不见、摸不着的,从信息科学的角度来说,我们通过观测所获得的,实际上是地磁场能量变化的信息.K指数仅是对此信息的一种简单、直观的表示,而在信息论中对信息更加规范的表示则是信息熵[10].信息熵的物理意义是“不确定性的量度",本文依据1997年北京地磁台的分钟观测数据,来计算地磁场K变化的信息熵,实际上就是以不确定性(熵)来解释不规则性(K变化).通过信息熵的计算,期望对地磁场所包含的信息量给出一个比较全面的度量.从理论上说,信息熵的大小与坐标系的选取无关,这就意味着,地磁场不规则变化的信息熵不取决于某个扰动程度最大的分量;同时注意到,HD的信息熵与XY的信息熵相等,HDZ的信息熵与XYZ,FDI的信息熵相等;另外,信息熵的大小不仅与扰动幅度有关,还与扰动次数有关.因此,如果用信息熵来衡量地磁场不规则变化的剧烈程度,可以避免上文指出的K指数的三个缺陷.本文的研究,帮助我们从信息论的角度,更加清楚地认识K指数的局限性,以及K指数与地磁场不规则变化的关系,并为急始型磁暴的早期自动识别提供了一定的理论指导[11].
2 地磁场各分量K变化的信息熵如何消去SR,本文采取的方法是:减去每月5个磁静日的平均日变化.通过这种处理,不但在很大程度上消去了Sq的干扰,而且基本上去除了地球主磁场长期变化的影响.由于L的幅度非常小,所以对信息熵的计算不会产生太大的影响.
下面,将依次计算地磁场各常用分量的信息熵,它们包括:X、Y、Z、H、D、I、F以及所谓K分量(将在2.3节定义).由于D和F的量纲是“分",而其他分量的量纲是“纳特",为了消除量纲的不同,D和I也将被化归为“纳特".信息熵的计算公式如下:
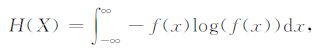
|
(1) |
公式(1)中的f(x)为随机变量X的分布密度函数.由于数据非常充足(每分钟一条记录,1997 年全年共有525,600条),所以用核方法可以非常准确地估计f(x)[12],因而依公式(1)算得的信息熵是比较准确的.
2.1 X、Y、Z、H、F分量的信息熵图 1的(a)、(b)、(c)、(d)、(e)分别是1997年北京地磁台分钟观测值H、X、Y、Z、F分量的直方图和概率密度核估计,由于样本十分充足,估计是十分准确的,并且没有出现边缘效应.将各分量的概率密度函数(估计)代入公式(1),得到它们的信息熵:

|
图 1 1997年北京地磁台分钟观测值各分量的直方图和密度估计 Fig. 1 Histogram and probability density of geomagnetic field based on the minute observations in 1997 from Geomagnetic Observatory Beijing |
H(X)=4.0161,H(Y)=3.1928,
H(Z)=2.6588,H(H)=4.0534,
H(F)=3.3267.
上述过程用到了“核估计"和“数值积分",其具体步骤可参看文献[12]和[13],本文不再赘述.计算结果表明,地磁场的北向分量X和水平分量H的信息熵几乎相等,而且比其他几个分量大.这说明我国地磁台标定K指数时,选用H分量是合理的.由于北京地磁台的磁偏角仅为-6°左右---X和H几乎相等,所以它们的信息熵也相差无几,比较图 1的(a)和(b)可知.
2.2 D、I分量的信息熵文献[14]指出:“对于连续型随机变量X,熵H(X)随标准差σ 的增大而增大",因此,对于不同量纲的随机变量无法比较信息熵.具体来说X、Y、Z、H、F分量的量纲是“纳特"而D和I分量的量纲是“分",要想比较它们之间的信息熵还须统一量纲,这就需要将D和I的量纲化为“纳特".值得注意的是,虽然磁通门磁力仪在测量D和I时,有一套类似的量纲转换机制,但是转换过程中一般都将H和F视为常数,本文则根据实测的H和F来进行量纲转换.
比较地磁场的7个分量可以发现:X、Y、Z、H、F分量的变化仅表现为地磁场在某一方向上强弱大小的变化,而D和I则表现为磁场的偏转.下面就以磁偏角D为例,详细阐述量纲的转化过程.D的变化表现为磁场在水平面上发生了一个偏转,参看图 2:H0 和H1 分别表示相继两时刻地磁场在水平面上的投影(矢量),ΔH表示H分量大小的变化---H分量的一阶差分(标量),ΔD表示D分量大小的变化---D分量的一阶差分(标量),图中不失一般性地假设ΔH为正(H分量增大了).易知,D的变化等效于矢量AB的长度,由于ΔD很小,所以|AB|≈ |H0| ×ΔD(D已经转换成弧度).在将ΔD等效为|AB|的同时,量纲也由“分或弧度"转化为了“纳特",本文将转化后的ΔD记作ΔD* ,其计算公式如下:
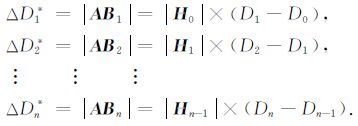
|
(2) |

|
图 2 D变化所产生的与H垂直的分量 Fig. 2 The element perpendicular to H element arisen from D variations |
公式(2)仅仅将ΔD的量纲转化为“纳特",如果将ΔD* 累加,便将D的量纲也转化为“纳特"了,本文将转化后的D记作D* ,其计算公式如下:

|
(3) |
其中D0*为累加的初始值,可以为任意常数,它的大小与信息熵无关,为了方便起见,将其设为零.公式(3)之所以成立,原因在于:D的变化非常小,以至于可以将AB1 至ABn累加的矢量和近似为标量和(矢量长度之和).按照同样的方法可以将I分量先转化为ΔI* 再转化为I*,计算公式如下:

|
(4) |
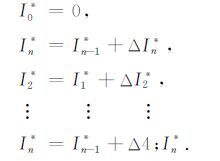
|
(5) |
图 3的(a)和(b)给出了D* 和I* 的直方图及概率密度估计,为了便于比较,同时也给出了H分量的直方图.由图中可见D* 和I* 的变化相对于H分量是不可忽略的,使用与2.1 节相同的方法得到H(D*)=3.2298、H(I*)=3.9663,其信息熵果然与H分量相差不大.

|
图 3 (a)1997年北京地磁台分钟观测值的概率密度函数:绿色直方图表示H分量,蓝色直方图表示量纲化为“纳特"的D分量-D*,红色曲线表示D*的概率密度估计;(b)1997年北京地磁台分钟观测值的概率密度函数:绿色直方图表示H分量,蓝色直方图表示量纲化为“纳特"的I分量-I*, 红色曲线表示I*的概率密度估计. Fig. 3 (a) The probability densities of minute observations tn 1997 from Geomagnetic Observatory Beijing: the green histogram is H element, the blue histogram s D element with the unit transformed to nT (.e.D*),and the red curve is the probability density estimation of D* ;(b) The probability densities of minute observations in 1997 from Geomagnetic Observatory Beijing: the green histogram is H element, the blue histogram is I element with the unit transformed to nT ( e.I*),and thered curve is theprobability density estimation of I* . |
在3小时内,如果X分量的扰动(幅度)大于Y分量,则K指数根据X分量标定,反之,则根据Y分量标定.这样很容易得到用于标定K指数的序列,我们称之为K分量:如果3小时内X分量扰动(幅度)大,则K分量就等于X分量;如果Y的扰动(幅度)大,则等于Y分量.因此,K分量事实上是一个包含X和Y的混合分量,它是K指数标定的基础.显然,K分量的信息熵是K指数所含信息量的上限.图 4是1997年北京地磁台分钟观测值K分量的直方图和概率密度核估计,通过计算得到H(K)=3.9486,因此,K指数至多只能包含熵为3.9486 的信息.

|
图 4 1997年北京地磁台分钟观测值K分量的直方图和密度估计 Fig. 4 Histogram and probability density of K element based on the minute observations in 1997 from Geomagnetic Observatory Beijing. |
可见,K分量的信息熵比X分量和H分量都要小,这就提示我们以扰动幅度最大的某个分量,来标定地磁场的扰动程度(标定K指数时就是这样)是有一定局限性的.
3 地磁场水平两分量K变化的信息熵信息熵的大小与坐标系的选取没有关系,如果用熵来表征地磁场的扰动程度,应该能够克服K指数的缺陷(1).下面,我们分别计算XY和HD的信息熵,考察它们是否一致.
首先,计算XY两分量的联合熵,为此齐玮等[15]设计了连续型随机向量联合熵的“离散方差分离"估计法.该方法分为“方差分离"和“离散"两个步骤:前者通过分离“标准熵"与“标准差对数和"来避免维数灾难;后者通过各分量的“最佳分割数"来离散连续型随机向量,从而避开了联合密度估计.具体步骤如下:
(1) 估计X、Y两分量的标准差,得到:

|
所以标准差的对数和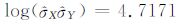
(2) 以均值代替期望,得到标准化的随机向量[X* Y*]T;
(3) 估计X* Y*]T 的边缘熵,得到:
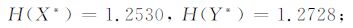
|
(4) 估计“最佳分割数",得到:

|
因此只需将X* Y*]T 分割成15×23=345个等面积的区间,不会发生维数灾难;
(5) 离散估计“标准熵",得到:

|
(6) 最后,

|
接下来,计算HD的信息熵,方法同上.在计算之前,应当先统一量纲,因为D的量纲是“分"而H的量纲是“纳特".也就是说,我们应当用上文的D*代替D进行计算.按照上面的六个步骤算得H(H,D*)=7.1950,与H(X,Y)几乎相等,可见信息熵的大小确与坐标系的选择无关.
以上的计算结果还表明:地磁场水平两分量K变化所包含的信息远远大于任何一个分量.所以说Reda[2]对K指数的质疑是有一定道理的:仅仅根据某个扰动最大的分量的3 小时最大扰幅,来表征地磁场的扰动程度,方法虽然简单,却可能丢失地磁场活动性的很多重要信息.
4 地磁场K变化的总信息熵起初,K指数的标定需要同时考虑地磁场的3个分量[1]---在3个分量中选择扰幅最大的分量.直到1963年,为了避免二次感应场的干扰,IAGA才决定K指数的标定不再考虑Z分量的3 小时扰幅.尽管Z分量混入了二次感应场的干扰,但这并不代表它不包含新的信息,标定K指数时不用Z分量,并不能说明Z分量就没有用:毕竟地磁场发生扰动时,各个分量都在扰动,而且各有特点.
下面继续用“离散方差分离"法来计算地磁场K变化的总信息熵(即XYZ三分量的联合熵),以此说明Z分量是否能提供水平方向两分量所不包含的信息,以及这样的信息量有多大.具体步骤如下:
(1) 估计X、Y、Z三分量的标准差,得到:

|
所以标准差的对数和
(2) 以均值代替期望,得到标准化的随机向量;[X* Y* Z*]T,
(3) 估计[X* Y* Z*]T的边缘熵,得到:
H(X*)=1.2530,H(Y*)=1.2728,
H(Z*)=1.3464;
(4) 估计“最佳分割数",得到:
binsX* = 15,binsY* = 23,binsZ* = 12,
因此只需将[X* Y* Z*]T 分割成15×23×12=4140个等体积的区间,不会发生维数灾难;
(5) 离散估计“标准熵",得到:
H(X* ,Y* ,Z*)=3.6613;
(6) 最后,
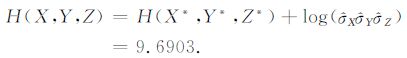
|
当然,地磁场的总信息熵也可以用H、D、Z和F、D、I来算,计算前首先要统一量纲---用D代替D* 、I代替I* .按照同样的步骤算得H(H,D* ,Z)=9.6734,H(F,D* ,I*)= 9.9264,结果与H(X,Y,Z)基本相同.其中,H(F,D* ,I*)的误差稍微大些,是D转化为D* 、I转化为I* 时有两次近似的结果.
这样,就得到H(X,Y,Z)- H(X,Y) =9.6903-7.2057 = 2.4846,表明Z分量确实能提供“新的信息",而且这些“新的信息"占地磁场总信息量的25.64%.可见,地磁场的三分量都包含着丰富的信息,即使是混入了二次感应场的Z分量.因此,在地球变化磁场的研究中,应充分利用地磁场三分量的信息,而不应该轻易对某些看似规律性不强的分量进行取舍.
基于以上观点,我们对急始型磁暴的早期自动识别进行了研究[15].众所周知,磁暴发生时,中低纬度地区地磁场H分量的变化最大、形态学特征最好,因而一般基于H分量来研究磁暴.然而,根据本文的计算结果,H分量不规则变化所包含的信息量,远小于地磁场三分量包含的总信息量.如果这一结论是正确的,那么,用地磁场三分量进行急始型磁暴自动识别的准确率,应高于仅用H分量自动识别急始型磁暴的准确率.
文献[15]的第七章,对1979 年至1999 年共260个急始型磁暴进行自动识别.实验分为两组,第一组基于H分量,第二组基于由XYZ三分量经非线性降维而得到的特征分量(文献[15]中称之为IsoDim),识别的方法都是概率神经网络,实验结果表明第一组的正确识别率约为75%,而第二组的正确识别率约为85%.这就表明,即使对于磁暴这种H分量形态学特征较好的不规则变化,仍有一部分信息包含在其余两个正交分量中.而正是由于本文对地磁场不规则变化信息熵的计算,使我们摒弃了“研究磁暴应选取形态学特征较好的H分量这一传统观念",采取了“基于地磁场三分量的急始型磁暴自动识别方案".
5 结语K指数作为一种重要的地磁活动指数,已有70多年的历史,在今后它仍将发挥重要的作用.因此,在使用K指数的同时,正确理解其含义、把握其缺陷是非常重要的.本文从信息论的角度,揭示了K指数的局限性,并指出如果用信息熵来表征地磁场的扰动程度,将能克服K指数的一系列缺陷.在今后的研究中,我们将逐步研究不同扰动程度下地磁场不规则变化的信息熵,以期找出一种更加合理的地磁活动指数.同时,本文研究发现,地磁场的三分量都包含着丰富的信息,如何综合运用地磁场三分量的信息来研究磁暴、亚暴、脉动等不同形式的地磁扰动,也是一个值得研究的问题.
| [1] | Bartels J, Heck N H, Johnston H F. The three-hour range index measuring geomagnetic activity. Geophys. Res. , 1939, 44(4): 411-454. DOI:10.1029/TE044i004p00411 |
| [2] | Reda J, Jankowski J. Three-hour activity index based on power spectra estimation. Geophys. J. Int. , 2004, 157: 141-146. DOI:10.1111/gji.2004.157.issue-1 |
| [3] | 朱岗崑. 关于佘山地磁场扰动变化的分析. 地球物理学报 , 2001, 44(Suppl.): 51–67. Tschu K K. Studies on the disturbance variations of geomagnetic field at So-Sè, near Shanghai,China. Chinese J. Geophys. (in Chinese) , 2001, 44(Suppl.): 51-67. |
| [4] | Xu W Y. Physics of Electromagnetic Phenomena of the Earth. Hefei: Chinese Science and Technology University Publishing House (in Chinese), 2009 . |
| [5] | 孙海军, 高守全. 喀什地磁台数字与模拟记录K指数对比分析. 内陆地震 , 2007, 21(4): 348–353. Sun H J, Gao S Q. Record and simulation record for KASHI geomagnetic station. Inland Earthquake (in Chinese) , 2007, 21(4): 348-353. |
| [6] | 程安龙, 周锦屏, 黄蔚北, 等. 中国地磁台网的K指数测量结果分析. 地震观测与研究 , 1998, 19(2): 48–55. Cheng A L, Zhou J P, Huang W B, et al. Analysis of measured K indices in geomagnetic observatory network of China. Seismological and Geomagnetic Observation and Research (in Chinese) , 1998, 19(2): 48-55. |
| [7] | 齐玮, 王秀芳, 李夕海, 等. 一种基于径向基神经网络的地磁场K指数实时标定方法. 地球物理学报 , 2010, 53(1): 147–155. Qi W, Wang X F, Li X H, et al. A real time K-indices scaling method based on radial basis neural network. Chinese J.Geophys. (in Chinese) , 2010, 53(1): 147-155. |
| [8] | Svalgaard L, Cliver E W, Le Sager P. IHV: A new long-term geomagnetic index, Adv. Space Res. , 2004, 34: 436-439. DOI:10.1016/j.asr.2003.01.029 |
| [9] | Mursula K. A new verifiable measure of centennial geomagnetic activity: Modifying the K index method for hourly data. Geophysical Research Letters , 2007, 34: L22107. DOI:10.1029/2007GL031123 |
| [10] | 钟义信. 信息科学原理. 北京: 北京邮电大学出版社, 2002 . Zhong Y X. Principles of Information Science (in Chinese). Beijing: Posts & Telecom Press, 2002 . |
| [11] | 齐 玮.辅助导航地磁变化场实时标识与建模研究.西安:第二炮兵工程学院,2009. Qi W. On variational geomagnetic field real time identifying and modeling for assistant navigation (in Chinese).[Doctor's Degree Dissertation]. Xi'an: Second Artillery Engineering Institute, 2009 |
| [12] | 范剑青, 姚琦伟. 非线性时间序列: 参数与非参数方法. 北京: 科学出版社, 2006 . Fan J Q, Yao Q W. Nonlinear Time Series: Nonparametric and Parametric Methods (in Chinese). Beijing: Science Press, 2006 . |
| [13] | (美)Gerald R 著.数值方法和MATLAB实现与应用. 伍卫国, 万 群, 张辉等译. 北京: 机械工业出版社, 2004 Gerald R. Numeric Method with MATLAB Implementation and Application (in Chinese), Translated by Wu W G, Wan Q, Zhang H, et al. Beijing: China Machine Press, 2004 |
| [14] | 常荷. 熵与方差. 开封教育学院学报 , 2001, 21(4): 43–44. Chang H. Entropy and variance. Journal of Kaifeng Institute of Education (in Chinese) , 2001, 21(4): 43-44. |
| [15] | 齐玮, 王仁明, 李夕海, 等. 连续型随机向量联合熵的离散方差分离估计. 数学的实践与认识 , 2010, 40(13): 102–109. Qi W, Wang R M, Li X H, et al. A discrete variance separation estimation to the joint entropy of continuous random vector. Mathematics in Practice and Theory (in Chinese) , 2010, 40(13): 102-109. |
 2011, Vol. 54
2011, Vol. 54


