2. 中国科学院上海天文台,上海 200030;
3. 总装备部北京指挥控制中心,北京 100000
2. Shanghai Astronomical Observatory, Chinese Academy of Sciences, Shanghai 200030, China;
3. Beijing Aerospace Command and Control Center, Beijing 100000, China
月球重力场是月球内部质量非均匀分布的一种反映,是研究月球内部构造以及月球演化的重要数据源[1].通过在频率域对月球地形和重力场进行相关与导纳分析,可以估计月球壳幔弹性厚度[2],有助于了解月球浅部结构;月球重力场低阶项位系数则对了解月球深部构造特征提供了很强的约束,低阶项位系数和月球天平动信息是确定月核密度、大小及状态的主要约束条件[3].
利用卫星轨道跟踪数据进行月球重力场模型解算的研究始于对1966年前苏联月球探测计划Luna10轨道跟踪数据的分析,后续的月球探测计划Lunar Orbiter系列任务和Apollo15/16,以及20世纪90年代发射的Clementine和Lunar Prospector(LP)探测器的轨道跟踪数据进一步提高了月球重力场模型解算精度.Clementine探测器为一极轨大偏心率轨道,有利于改进月球重力场低阶项位系数的精度[4],LP 为一极轨圆轨道卫星,正常任务段平均轨道高度为100km, 扩展任务段平均轨道高度为30km, 适合于解算月球重力场中高阶项位系数,并有利于提高月球正面重力场的精度和空间分辨率[5].
由于月球自转和公转周期近似相等,导致月球只有一面对着地球,使得对月球卫星的直接观测仅限于月球正面区域.为了克服这一局限,日本月球探测计划SELENE 通过高轨-低轨卫星跟踪卫星模式首次直接探测了月球背面重力场[6].这一计划的成功实施极大地改进了当前月球重力场模型的精度,特别是精化了月球背面重力场,给出了月球背面典型盆地区域重力异常的环状特性,即中心区域为大的负重力异常,外层由正的重力异常包围.这些特征为进一步了解月球正面和背面壳幔结构的二分性以及月球热演化历史提供了新的信息[6].
用于月球重力场模型解算的主要轨道跟踪数据均来自对极轨道卫星的跟踪,这一倾角的轨道可以最大程度地覆盖月球表面,但不利于降低月球重力场特定阶次位系数之间的相关性.地球重力场的解算面临类似问题.为了降低地球重力场位系数之间的相关性,解算EGM96 重力场模型时综合了历史上不同倾角的卫星轨道跟踪数据[7].图 1给出了不同倾角情况下月球重力场模型误差引起的轨道误差在轨道面径向、沿迹及法向的分布情况.可以看出,仅用极轨卫星轨道跟踪数据解算得到的月球重力场模型,对极轨这一轨道的卫星具有较好的轨道预报精度,随着倾角偏离极轨的程度越大,轨道预报精度越差[8, 9].
我国“嫦娥一号"正常任务期间积累了大量轨道跟踪数据,并成功用于月球重力场模型解算[9, 10],原拟定在任务后期进行变轨,以一定倾角轨道进行月球地形及重力场探测,由于星上机械故障这一计划未能实施.“嫦娥二号"已于2010年10月发射,在正常任务期间有望调整轨道倾角进行跟踪测量.本文针对现有月球重力场模型解算中主要用到极轨卫星这一情况,仿真分析了利用90°倾角卫星90天时段长度、77°倾角卫星90 天长度以及综合45 天90°倾角卫星与45天77°倾角卫星三种情况下月球重力场仿真解算的情况(90°倾角解算得到的模型记为B,77°倾角解算得到的模型记为C,90°与77°综合解算得到的模型记为D,见后文),对各解算模型进行了位系数功率谱分析、基于解算模型位系数协方差矩阵进行了月球重力异常和月球大地水准面误差分析以及精密定轨分析.这一研究主要针对我国后续月球探测计划的科学目标,以提出更有特色的月球重力场探测模式.
2 仿真计算设置仿真过程中选择LP100J[5]模型为真实模型.利用LP100J模型生成三种观测模式下的真实观测量,观测类型包括青岛和喀什两个站的双程测速观测量,以及中国VLBI网(上海、北京、昆明、乌鲁木齐)四个台站的时延和时延率观测量.VLBI时延的精度设定为3ns, 时延率的精度设定为1ps/s, USB双程测速的精度为1mm/s.仿真解算中在真实观测量的基础上增加高斯白噪声,其标准偏差值为测量数据精度.仿真时段为2010年5月1日至2010年8月1日.数据仿真中考虑到月球的遮掩,测站地面高度角设定为10°.
考虑到我国后续月球探测的轨道设计,三种仿真模式中轨道高度均选取为100km, 极轨和77°倾角轨道下的偏心率均为0.0005,接近于圆轨道.模拟计算中用到的动力学模型包括月球非球形引力摄动,太阳和地球的引力摄动,木星、水星、金星等大行星的摄动,固体潮摄动,地球扁率的间接效应,太阳光压摄动以及相对论效应.计算过程中采用的坐标系是J2000.0月心天球坐标系,时间系统为UTC 协调世界时,日月等天体的位置采用JPL DE405/LE405[11]历表计算.计算中采用了GSFC/NASA/USA 授权使用的轨道分析软件GEODYN II/SOLVE[12, 13].
月球重力场模型解算采用动力法[4, 5],即在精密定轨的同时解算重力场位系数.各模型求解的阶次设定为50×50,该阶次对应的月球表面水平分辨率为100km[14].由于仿真观测数据只有月球正面的观测数据,在求解中需要加入Kaula先验约束以平滑重力场参数的求解[4, 5].基于动力法求解月球重力场位系数涉及到非线性问题的线性化,为了提高解算精度,解算需要迭代处理.文中迭代次数为2次,迭代收敛准则为观测量残差达到先验误差水平.进行精密定轨及重力场参数解算时采用的先验重力场模型为在LP100J的基础上加上模型各位系数对应的3倍方差.考虑到轨道运行过程中的姿态调整,解算弧段长度选取为1 天,以避免动量轮卸载因素对精密定轨及重力场解算的影响.
3 月球重力场模型功率谱分析基于球谐函数展开的月球重力场模型位系数的阶方差信息可以反映重力场在频域中的信号强度(图 2中sig).阶方差的计算公式为[15]
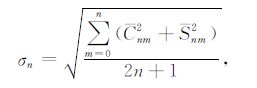
|
(1) |
式中Cnm,Snm是正则化的位系数,n为阶,m为次.对阶方差信息进行分析判断的常用工具是Kaula准则.Kaula准则是对重力场模型位系数统计规律的一个近似描述,即正则化的位系数具有零均值,标准偏差与阶数n的平方成反比[16],其数学表达形式为
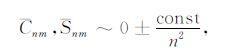
|
(2) |
计算中常数const取值为3.0.在月球重力场模型确定中引入Kaula准则的目的主要是作为一个正则化因子,用来克服由于缺乏月球背面轨道跟踪数据导致重力场求解时的不稳定性,同时对高阶位系数的计算起到一平滑作用[17].Kaula准则用曲线3.0×10-4/n2 进行描述,其中n对应重力场模型位系数的阶数.
月球重力场模型的误差阶方差用来反映重力场位系数误差在频域中的强度(图 2 中sigvar),可以说明重力场解算模型的精度水平,其计算公式为[16]
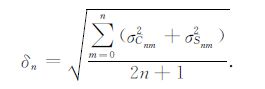
|
(3) |
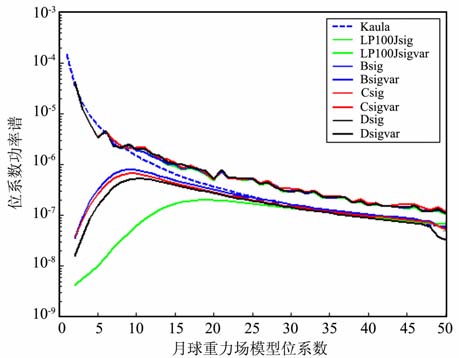
图 2给出了解算模型与先验模型的功率谱曲线图,图中B,C 和D 分别表示仅用90°倾角卫星、仅用77°倾角卫星、以及综合两颗卫星解算得到的重力场模型.由图 2可以看出,三种计算模式下得到的重力场模型与真实模型均比较接近,且模型D 得到的阶方差与先验真实模型更为接近.相比于先验真实模型LP100J,三个解算模型对中长波部分位系数没有显著改进.这是因为LP100J解算中综合了历史高轨道跟踪数据,包括Clementine和Apollo 及Lunar Orbiter系列探测器,这些探测器的轨道跟踪数据对改进中长波重力场信息起到了重要作用.从图 2中可以看到不同倾角轨道跟踪数据对重力场位系数相对改进的程度,77°倾角卫星跟踪数据解算的模型相比于极轨卫星而言,对5阶次到15阶次位系数精度有比较明显的改进,这可能是因为77°倾角的月球卫星轨道相比于极轨有利于降低特定阶次扇谐系数和田谐系数的相关性.融合极轨与77°倾角卫星的跟踪数据联合解算的重力场模型,则对2 至15阶次的位系数精度有显著改进,这主要是由于综合不同倾角卫星的轨道跟踪数据,降低了特定阶次位系数之间的相关性,从而提高了位系数的解算精度.
4 月球重力异常及月球大地水准面误差分析基于误差传播理论,利用解算模型得到的位系数协方差矩阵进行了月球重力异常及月球大地水准面误差分析.月球重力异常和月球大地水准面的计算公式分别为[15]
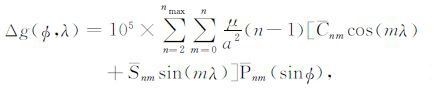
|
(4) |
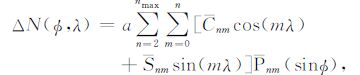
|
(5) |
其中a是月球平均半径,(φ,λ)为月面地理经纬度,μ为月球引力质量常数,n和m分别为重力场位系数的阶与次,nmax为模型的最大截断阶数,Pnm为连带勒让德函数.(4)(5)两式可以简化为线性关系式:

|
(6) |
式中x表示位系数参数向量,y表示月球重力异常或者月球大地水准面,两者之间通过矩阵算子H联系.令通过模型解算得到的重力场位系数协方差矩阵为Q(x),则通过误差传播定律有

|
(7) |
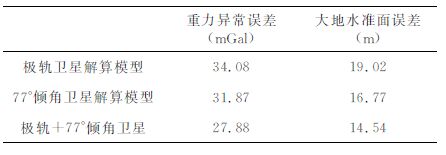
其中σ(y)为y的方差.基于三种解算模式得到的月球重力异常及月球大地水准面误差计算情况如表 1所示.由表 1可以明显看出,综合极轨和77°倾角卫星进行解算的情况具有最小的月球重力异常和月球大地水准面误差,由77°倾角卫星解算模型得到的月球重力异常和大地水准面精度相比于90°倾角卫星解算模型均有提高,这与图 2 中关于各模型位系数误差阶方差的区别一致.
|
|
表 1 月球重力异常和月球大地水准面RMS值 Table 1 RMS of lunar gravity anomaly and selenoid |
|
图 2 Kauk曲线,极轨、77°倾角以及极轨和77°倾角综合解算得到的重力场、真实重力场与先验重力场模型位系数阶方差及误差阶方差曲线 Fig. 2 Kaula constraint, degree wise sigma and error sigma of gravity field solution based on polar orbit, 77° inclination orbit, polar plus 77° inclination orbit, truth orbit and a prior orbit |
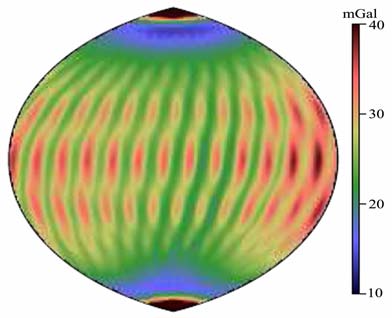
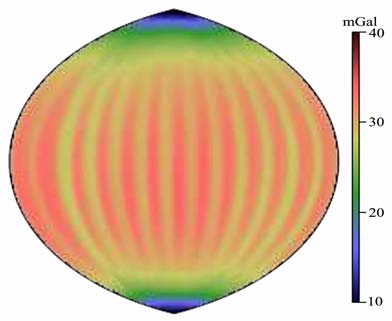
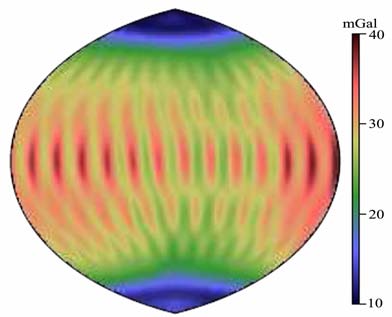
图 3至图 5给出了基于三个解算模型的位系数协方差矩阵计算得到的月球正面重力异常误差分布图.图 3中的误差分布呈比较明显的倾斜条纹形式,这主要是由于卫星的轨道特征,导致卫星轨道跟踪数据星下点覆盖呈倾斜条纹形式.图中红色部分较大的重力异常误差区域是由于没有跟踪数据覆盖所引起,77°倾角的轨道无法覆盖两极,导致在两极区域有较大的重力异常误差.图 4 中重力异常分布呈现明显的过两极的条带特性,在高纬度及两极具有较小的重力异常误差,这是由于极轨卫星跟踪数据星下点分布在两极与中高纬度地区更为密集.图 5给出的综合极轨和77°倾角卫星得到的重力异常误差分布相比于图 3和图 4 均有所改进,图 5 中重力异常误差分布的倾斜条带效应相比于图 4有较为显著的弱化,重力异常精度有明显提高.这从月球重力场特征量误差分布的角度证实了倾角卫星对改进月球重力场模型精度的贡献.
|
图 3 77°倾角卫星解算重力场模型对应的月球正面重力异常误差分布 Fig. 3 Lunar nearside gravity anomaly distribution based on gravity field model from77° inclination orbit |
|
图 4 极轨卫星解算重力场模型对应的月球正面重力异常误差分布 Fig. 4 Lunar nearside gravity anomaly distribution based on gravity field model from polar orbit |
|
图 5 极轨卫星与77°倾角卫星联合解算重力场模型对应的月球正面重力异常误差分布 Fig. 5 Lunar nearside gravity anomaly distribution based on gravity field model from 77° inclination orbit plus polar orbit |
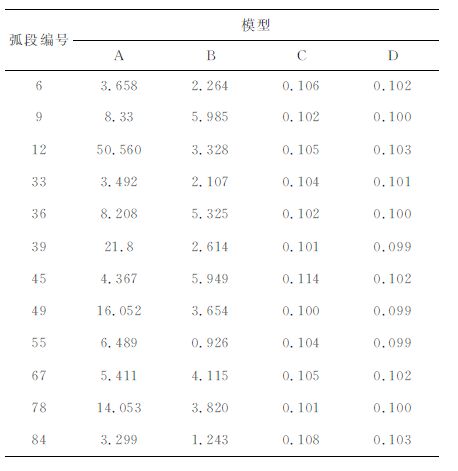
为了进一步验证倾角卫星在提高月球重力场模型解算精度中的贡献,利用不同重力场模型对77°倾角卫星进行了精密定轨.精密定轨中涉及到的其他动力学模型及参考框架与第2 节中一致.考虑的重力场模型包括带有误差的先验重力场模型(A)、极轨卫星解算得到的模型(B)、77°倾角卫星解算得到的模型(C)以及综合极轨卫星和77°倾角卫星解算得到的模型(D).随机选取了12 个弧段,弧段按照天数进行编号,精密定轨后给出的参考量为双程测速残差.结果如表 2所示.
|
|
表 2 不同重力炀模型精密定轨后双程测速残差RMS值(单位:cm/s) Table 2 RMS of two-way range rate residuals after precise orbit determination based on different gravity field models (unit :cm/s) |
由表 2可以看出,基于带有误差的先验重力场模型进行精密定轨时,具有较大的残差,以极轨卫星跟踪数据解算得到的重力场模型相比于先验重力场模型有所改进,但误差仍然较为显著,这说明基于极轨卫星得到的重力场模型不能较好地应用到其他倾角卫星轨道上,这与图 1 中给出的轨道预报误差分布一致.利用77°倾角卫星跟踪数据解算得到的重力场模型具有较好的精密定轨结果,这是因为该重力场模型完全是由这一卫星轨道的跟踪数据解算所得,故具有较好的拟合程度.综合极轨和77°倾角卫星跟踪数据解算得到的重力场模型可以得到最小的轨道残差值,并能恢复到先验测量精度水平.这主要是因为综合极轨和77°倾角卫星的轨道跟踪数据,通过降低特定阶次位系数之间的相关性,提高了重力场模型解算精度.表 2 的数据一方面说明了整个仿真计算过程的准确性,另外也说明为了满足未来某一特定倾角月球卫星精密定轨的需求,需要综合不同倾角卫星的轨道跟踪数据进行综合解算以得到高精度月球重力场模型.
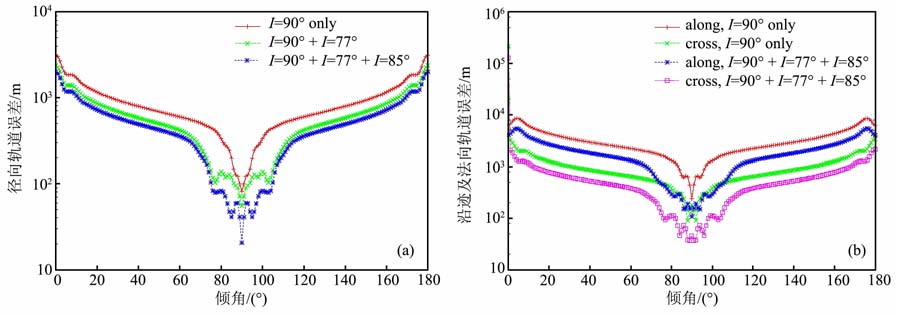
|
图 1 2个月极轨、2个月极轨+ 2个月77°倾角、2个月极轨+ 2个月77°倾角+2个月85°倾角轨道得到的月球重力场对卫星轨道精度的影响:(a)是对月心-卫星径向的影响,(b)是对卫星沿轨迹和垂直于轨道面两方向的影响 Fig. 1 Effect on orbital accuracy of lunar gravity tield based on polar orbit in 2 months, polar orbit in 2 months plus 77° |
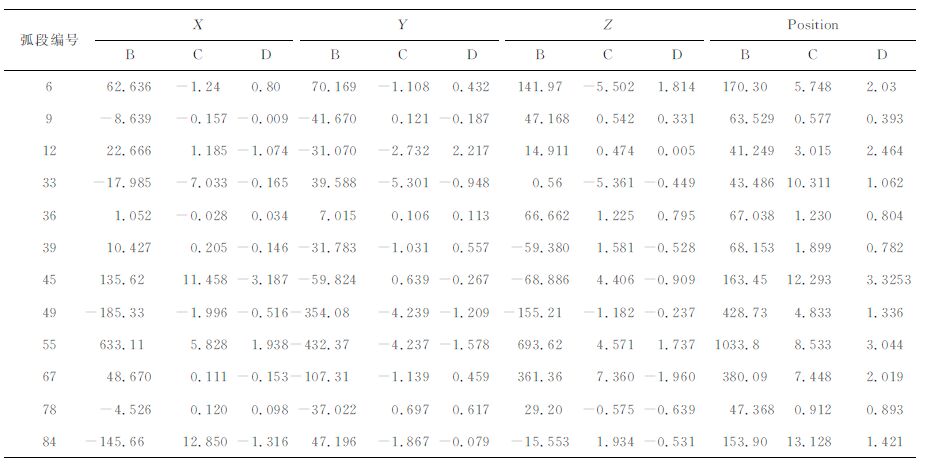
考虑到仿真解算中已知真实轨道信息,为了更客观地评价重力场模型精度,利用三个不同模型对77°倾角卫星进行了精密定轨.表 3给出了三种情况下解算轨道与真实轨道的差值.由表 3可以看出,综合极轨和大倾角卫星跟踪数据解算得到的重力场模型(D)具有最好的定轨精度.基于三个不同重力场模型进行精密定轨后,位置误差的均值分别为221.75m, 5.82m, 1.63m, 对应的标准偏差为286.68m, 4.49m, 0.94m, 可以看出模型D 的定轨精度相比于B,改进超过两个量级,相对于C 改进达5 倍.仅根据极轨卫星轨道跟踪数据解算得到的重力场模型(B)对倾角卫星定轨具有较大的误差,这与表 2得出的结论一致.部分弧段中仅用倾角卫星得到的轨道(C)和(D)具有较为接近的结果,这些弧段主要是轨道面接近通视的情况,即轨道面垂直于地面测站到探测器连线方向,这一几何构型下具有更长的观测时段,可以对轨道起到较好的约束效果.
|
|
表 3 不同重力炀模型精密定轨结果(单位:m) Table 3 Precise orbit deter mination based on different gravity field models(unit:m) |
本文针对我国后续月球探测计划可能改变倾角,在近极轨道附近以大倾角轨道运行,综合这一倾角轨道的跟踪数据进行重力场模型解算有利于降低月球重力场模型特定阶次位系数之间的相关性,以起到提高月球重力场模型解算精度的作用.另外已有重力场模型的解算数据主要来自于极轨卫星,这一模型对其他倾角的卫星具有较大的轨道预报误差.基于上述考虑,本文针对仅用极轨卫星,仅用77°倾角卫星以及综合极轨卫星和77°倾角卫星三种情况,进行了月球重力场模型仿真计算.从重力场位系数功率谱、月球重力异常及大地水准面误差、精密定轨等方面对三个解算模型进行了精度评价.结果表明综合极轨卫星和77°倾角卫星得到的月球重力场模型,相比于只使用一种倾角的卫星解算得到的模型,在中低阶次位系数精度有显著改进,由此可以得到更为精确的月球重力异常及月球大地水准面分布,并在定轨精度上有大幅提高.本文计算结果可以对我国后续月球探测计划用于月球重力场探测提供一定程度的参考.
致谢本文所提及的GEODYNII轨道分析软件是经GSFC/NASA/USA 授权中国科学院上海天文台使用,并且在上海天文台的计算机工作站上完成.
| [1] | Khan A, Mosegaard K, Williams J G, et al. Does the Moon possess a molten core? Probing the deep lunar interior using results from LLR and lunar prospector. J. Geophys. Res. , 2004, 109. DOI:10.1029/2004JE002294 |
| [2] | Crosby A, McKenzie D. Measurements of the elastic thickness under ancient lunar terrain. Icarus , 2005, 173(1): 100-107. DOI:10.1016/j.icarus.2004.07.017 |
| [3] | Hanada H, Iwata T, Namiki N, et al. VLBI for better gravimetry in SELENE. Advances in Space Research , 2008, 42(2): 341-346. DOI:10.1016/j.asr.2007.11.003 |
| [4] | Lemoine F G, Smith D E, Zuber M T, et al. A 70th degree lunar gravity model (GLGM-2) from Clementine and other tracking data. J. Geophys. Res. , 1997, 102(E7): 16339-16359. DOI:10.1029/97JE01418 |
| [5] | Konopliv A S, Asmar S W, Carranza E, et al. Recent gravity models as a result of the Lunar Prospector mission. Icarus , 2001, 150(1): 1-18. DOI:10.1006/icar.2000.6573 |
| [6] | Namiki N, Iwata T, Matsumoto K, et al. Farside gravity field of the Moon from four-way Doppler measurements of SELENE (Kaguya). Science , 2009, 323(5916): 900-905. DOI:10.1126/science.1168029 |
| [7] | Lemoine F G, Kenyon S C, Factor J K, et al. The development of the joint NASA GSFC and the National Imagery and Mapping Agency (NIMA) geopotential model EGM96. NASA Technical Paper NASA/TP-1998-206861. Goddard Space Flight Center, Greenbelt., 1998 |
| [8] | Rosborough G W, Tapley B D. Radial, transverse and normal satellite position perturbations due to the geopotential. Celestial Mechanics , 1987, 40(3-4): 409-421. DOI:10.1007/BF01235855 |
| [9] | 鄢建国, 李斐, 平劲松, 等. 基于嫦娥一号跟踪数据的月球重力场模型CEGM01. 地球物理学报 , 2010, 53(12): 2843–2851. Yan J G, Li F, Ping J S, et al. Lunar gravity field CEGM01 based on Chang' E-1 orbital tracking data. Chinese J. Geophys. (in Chinese) , 2010, 53(12): 2843-2851. |
| [10] | Yan J G, Ping J S, Li F, et al. Chang'E-1 precision orbit determination and lunar gravity field solution. Advances in Space Research , 2010, 46(1): 50-57. DOI:10.1016/j.asr.2010.03.002 |
| [11] | Standish E M. JPL planetary and lunar ephemerides, DE405/LE405. Interoffice Memorandum , 1998, 312. |
| [12] | Rowlands D, Marshall J A, Mccarthy J, et al. GEODYN Ⅱ system description. Vols.1-5, ontractor report, Hughes STX Corp., Greenbelt, MD,1997 |
| [13] | Ullman R E. SOLVE program: mathematical formulation and guide to user input. Hughes/STX Contractor Report, Contract NAS5-31760. NASA Goddard Space Flight Center, Greenbelt, Maryland, 1994 |
| [14] | 陈俊勇, 宁津生, 章传银, 等. 在"嫦娥一号"中求定月球重力场. 地球物理学报 , 2005, 48(2): 275–281. Chen J Y, Ning J S, Zhang C Y, et al. On the determination of lunar gravity field in the Chinese first lunar prospector mission. Chinese J. Geophys. (in Chinese) , 2005, 48(2): 275-281. |
| [15] | Heiskanen W A, Moritz H. Physical Geodesy. San Francisco: Freeman,1967 |
| [16] | Kaula W M. Theory of Satellite Geodesy. Waltham, mass: Blaissell Publishing Company,1966 |
| [17] | 鄢建国, 平劲松, 李斐, 等. 应用LP165.P模型分析月球重力场特征及其对绕月卫星轨道的影响. 地球物理学报 , 2006, 49(2): 408–414. Yan J G, Ping J S, Li F, et al. Character analysis of the lunar gravity field by the LP165P model and its effect on lunar satellite orbit. Chinese J. Geophys. (in Chinese) , 2006, 49(2): 408-414. |
 2011, Vol. 54
2011, Vol. 54