目标在电磁波照射下,除了有幅度、相位、频率的响应外,还存在变极化效应.极化是电磁波共有的一种性质,通过改变雷达发射天线和接收天线的方向就可以改变电磁波的极化方式.电磁波与目标表面发生作用后,目标会使电磁波极化产生不同程度的旋转.全极化雷达采用不同的天线耦合方式来接收地质体的各种极化信息,不但能获取共极化信息而且能接收交叉极化信息,通过对极化信息的分析和处理,可以达到识别地下目标的多种属性的目的,在目标探测和识别上有着强大的优势.自然界中,地面、海面、地下矿体表面均可以看成是满足某种特定概率密度分布的粗糙表面,对随机粗糙表面及其标定的研究在勘探地球物理领域中也有着重要应用价值.火山岩油气藏中经常会出现各种原因形成的裂缝,影响着对火山岩油气藏的勘探和开发,裂缝的诊断评估技术越来越受到广泛重视.2003 年Zhou 和Sato利用地面极化SAR 系统在环境领域进行了初探[1, 2].2007年Kovalenko,Yarovoy等利用探地雷达极化特征对地雷进行了探测[3],都取得了比较好的效果.
但当前探地雷达由于其天线极化方式单一,不能使用极化信息,一般只利用电磁波的幅度、相位、频率等属性[4~6],所以对探地雷达极化特征的研究比较困难.而正演模拟是获取探地雷达极化信息,研究探地雷达极化特性的简单而重要方法.本文在时域有限差分(FDTD)法的基础上,构建了全极化探地雷达的正演模拟方法,通过水平正交双方向同时接收来获取全极化信息,对全极化雷达进行了正演模拟,并通过实验验证了正演模拟的正确性和有效性.
2 全极化探地雷达正演模拟方法 2.1 时域有限差分法FDTD 法是麦克斯韦方程的直接时域法,具有计算简单、直观、灵活性强、计算精度高、动态范围大等优点[7, 8],因此,本文在它的基础上构建全极化探地雷达正演模拟方法.在笛卡尔坐标系下,对麦克斯韦方程进行中心差分离散,得到形如(1)式的电场和磁场的离散表达式[9~11]:
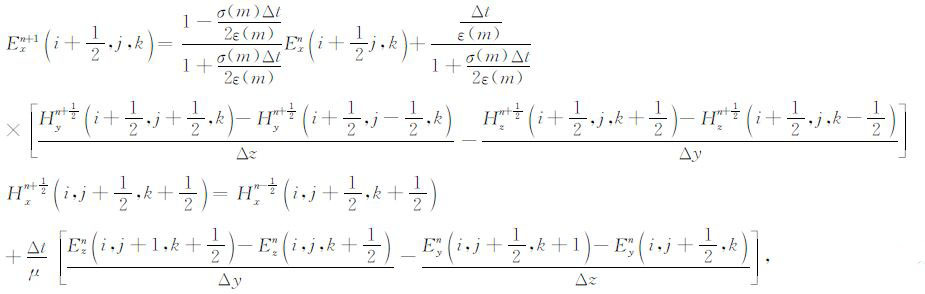
|
(1) |
其中m=(i+1/2,j,k),i,j,k是x,y,z的离散点序号;n是时间离散序号;Δt是时间离散间隔;Δx,Δy,Δz为对应坐标轴的空间离散间隔.ε、μ、σ 分别为介质的介电常数、磁导率、电导率(单位为S/m).电磁场的y,z分量的离散化形式与(1)式类似.
因为吸收边界条件采用单轴各向异性介质完全匹配层(UPML),UPML 较PML 有更好的吸收效果[12~14].另外,形如(1)式的差分方程是Maxwell方程近似得到的一组耦合差分方程,因而需要考虑离散后差分方程组解的稳定性[15, 16].差分格式(1)的稳定性条件为:
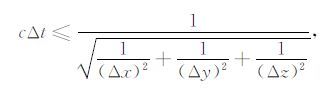
|
(2) |
其中c=1/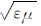
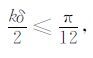
|
(3) |
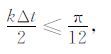
|
(4) |
式中,空间步长δ 分别等于Δx,Δy,Δz,k=2π/λ,λ为无色散介质中的波长.
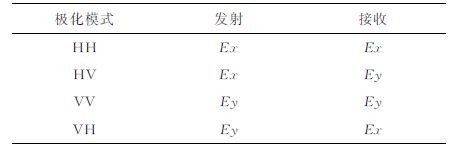
2.2 全极化模拟方法全极化探地雷达有四种极化方式,分别是HH、HV、VV、VH,其中HH 和VV 为共极化模式,HV和VH 为交叉极化模式.在正演模拟中,通过将源分别加在水平正交的两个电场分量上,水平正交双方向同时接收电场分量,来实现全极化探地雷达的四种极化模式(表 1).
|
|
表 1 全极化探地雷达正演模拟极化模式组合表 Table 1 Polarimetric model for forward modeling of the full-polarimetric GPR |
由于在笛卡尔坐标系下具有对称性,所以在正演模拟计算时,通常只选择VH 和VV 两种极化模式,即将发射源只加在Ey电场分量上,通过接收Ey电场分量模拟VV 极化模式,通过接收Ex电场分量模拟VH 极化模式.
3 全极化探地雷达标准测试目标的正演模拟和实验室实验分别对水平金属板和金属角反射器两种标准测试目标进行实验室实验和三维正演模拟计算.
3.1 水平金属板和金属角反射器目标正演模拟三维计算空间的大小为0.8m×0.8m×1.0m,发射天线和接收天线间距为0.05m.发射源为线性极化的雷克子波,中心频率为1GHz.
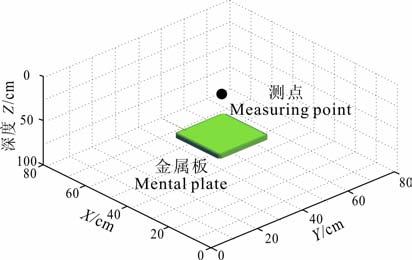
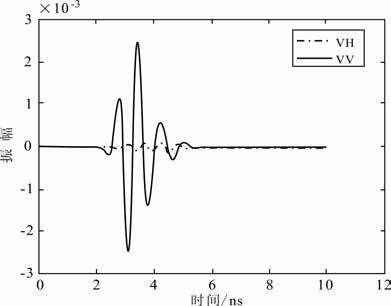
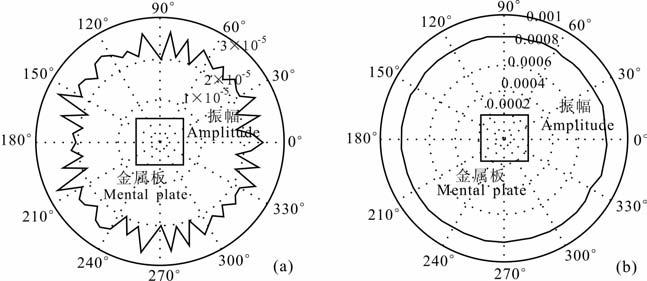
水平金属板正演模型如图 1所示,金属板的板厚为0.01 m,长宽各0.1 m,相对介电常数εr=8、μ=μ0=4π×107 H/m、σ=104S/m.测线和金属板的距离为0.9 m.图 2显示天线位于金属板中心点正上方处的VH 和VV 的响应信号.交叉极化响应很弱,共极化响应较强.另外,在金属板中心点正上方的位置,将天线围绕着Z轴,做360°旋转模拟计算,每5°进行一次.图 3(a,b)分别显示VH 和VV极化模式下获取的响应信号振幅绝对值的最大值,共极化和交叉极化的响应特征基本上与观测角度无关.
|
图 1 三维水平金属板正演模型 Fig. 1 3D model of metal plate |
|
图 2 正演模拟金属板中心点处的共极化和交叉极化响应信号 Fig. 2 Simulated signals of co-polarization and cross |
|
图 3 正演模拟交叉极化模式(a)和共极化模式(b)下金属板全角度响应 Fig. 3 Simulated full angle responses of cross-polarization (a) and co-polarization (b) above the metal plate |
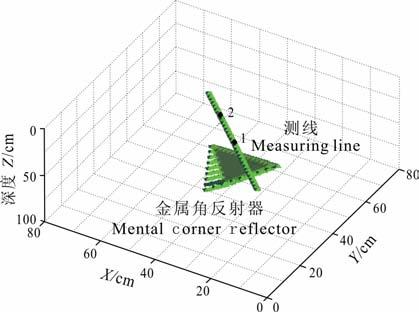
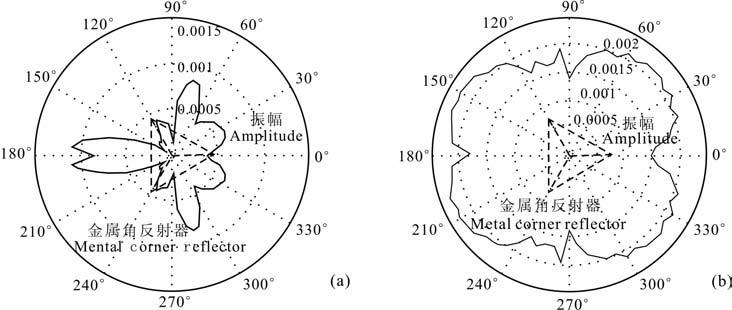
金属角反射器模型如图 4所示,金属角反射器的板厚为0.01 m,各边长度为0.1 m,并且三个面分别和水平面成45°角,εr=8,μ=μ0,σ=104 S/m.底角距测线的距离为1.1m.保持天线间距0.05m不变,选择与金属角反射器一边成15°角的测线,天线沿测线移动,测点1和测点2分别在金属角反射器的中心点正上方位置和边缘正上方位置.图 5(a,b)分别显示测点1和测点2的VV 和VH 极化响应信号,测点1处的共极化响应强于交叉极化响应,而测点2处的交叉极化响应强于共极化响应.同样,在金属角反射器中心点正上方的位置,将天线围绕着Z轴作360°旋转模拟计算,每5°进行一次.图 6(a,b)分别显示VH 和VV 极化模式下获取的响应信号振幅绝对值的最大值,共极化响应对观测角度不是很敏感,但交叉极化响应随角度的变化呈T 字形,对观测角度很敏感.
|
图 4 三维金属角反射器正演模型 Fig. 4 3D model of metal corner reflector |
|
图 5 正演模拟金属角反射器测点1处(a)和2处(b)的共极化和交叉极化响应信号 Fig. 5 Simulated signal of co-polarization and cross-polarizationat the point 1(a) ,point 2(b) of metal corner reflector |
|
图 6 正演模拟交叉极化模式(a)和共极化模式(b)下金属角反射器全角度响应 Fig. 6 Simulated full angle responses of cross-polarization (a) and co-polarization (b) above the metal corner reflector |
在实验室分别对金属板(图 7)目标和金属角反射器(图 8)目标进行了极化测量实验.实验采用极化步频探地雷达系统[17],该系统由矢量网络分析仪、Vivaldi天线、pc控制单元(计算机)和XYZ 位置控制器组成.Vivaldi天线有VV、HH、VH、HV四种组合方式,能进行全极化测量.本次共进行了两组实验.

|
图 7 金属板目标 Fig. 7 Target of metal plate |

|
图 8 金属角反射器目标 Fig. 8 Target of metal corner reflector |
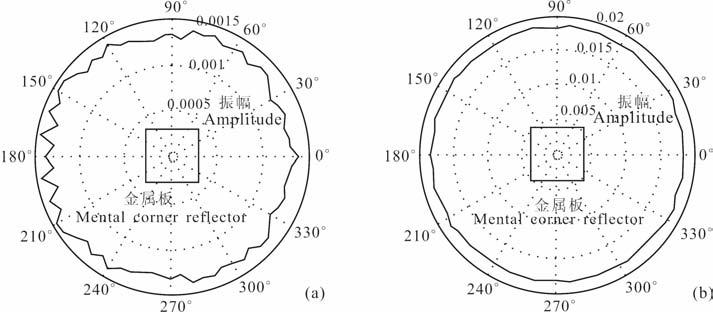
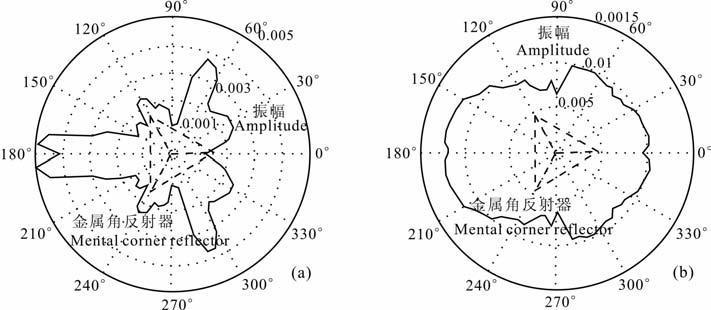
第一组实验将发射天线放置在金属板和金属角反射器的中心点正上方位置,天线围绕着Z轴进行360°旋转观测,每5°进行一次观测记录.图 9(a,b)分别显示金属板目标的VH 和VV 极化模式下获取的响应信号振幅绝对值的最大值;图 10(a,b)分别显示金属角反射器目标的VH 和VV 极化模式下获取的响应信号振幅绝对值的最大值.金属板目标的共极化和交叉极化的响应特征基本上与观测角度无关,而金属角反射器的交叉极化的响应对观测角度很敏感,随角度的变化呈T 字形.
|
图 9 实验测试交叉极化模式(a)和共极化模式(b)下金属板全角度响应 Fig. 9 Full angle response acquired in cross-polarization (a) and co-polarization (b) model above the metal plate |
|
图 10 实验测试交叉极化模式(a)和共极化模式(b)下金属角反射器全角度响应 Fig. 10 Full angle response acquired in cross-polarization (a) andco-polarization (b) model above the metal corner reflector |
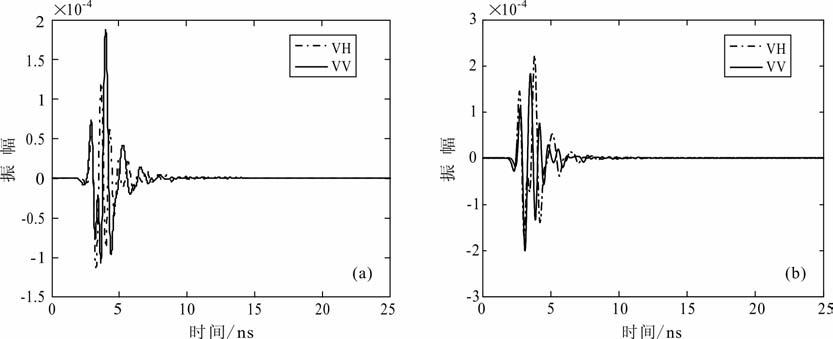
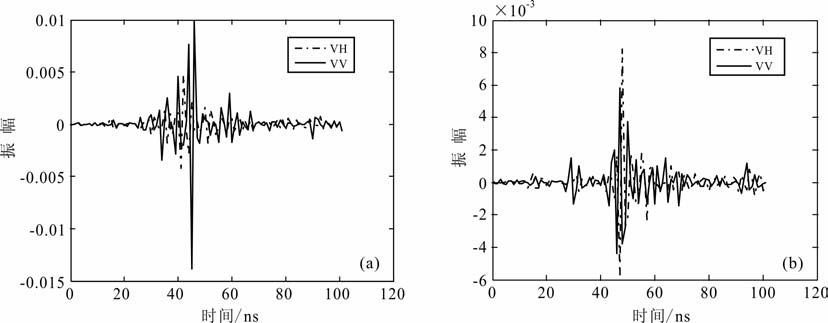
第二组实验选择在金属角反射器的中心点正上方位置和边缘正上方位置,天线沿着与角反射器一边成15°的测线进行布置.图 11(a,b)分别显示在两个观测位置处的VH 和VV 极化模式下获取的响应信号.中心点附近的VV 反射信号强于VH 反射信号,而边缘处VH 反射信号强于VV 反射信号.
|
图 11 实验测试金属角反射器中心点(a)和边缘处(b)的共极化和交叉极化响应信号 Fig. 11 Signal of co-polarization and cross-polarization acquired above the middle point (a) ,the edge (b) of metal corner reflector |
对比实验和正演模拟结果可以看出,实验和正演模拟具有很好的一致性,说明该正演模拟方法可以有效地模拟全极化探地雷达信号.从全角度响应图来看,金属板目标的实验和模拟的共极化和交叉极化的响应特征与观测角度无关;而金属角反射器目标的实验和模拟的响应特征与观测角度有关,特别是交叉极化的响应对观测角度很敏感,全角度响应图形状呈T 字形.从极化角度看,实验和模拟的结果显示,共极化在两种目标体情况下对观测角度都不是很敏感;而交叉极化则在金属角反射器目标体情况下对观测方位很敏感.另外,从金属角反射器的响应信号来看,实验和正演模拟的结果都显示,交叉极化响应振幅和共极化响应振幅的相对大小会随着观测点位置的变化而发生变化.因此,交叉极化响应和共极化响应信息的综合使用有助于对目标的形状、方位等属性进行识别判断.
4 全极化探地雷达随机表面和倾斜裂缝目标的正演模拟自然界中,地面、海面均可以看成是满足某种特定概率密度分布的粗糙表面,随机粗糙表面的电磁散射特性研究在国防军事领域和民用技术领域都具有显著的学术价值,对随机表面及其标定的研究在勘探地球物理领域中也有着重要应用价值[18~20].火山岩油气藏中经常会出现各种原因形成的裂缝,影响着对火山岩油气藏的勘探和开发,所以裂缝的诊断评估技术越来越受到广泛重视.本文用所研究的正演模拟方法模拟随机表面和倾斜裂缝目标的雷达响应,探讨这两种目标的极化响应特征.
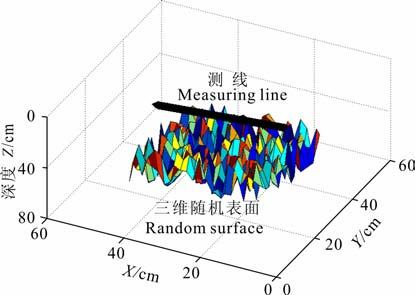
4.1 随机表面目标为了检验全极化测量对物体表面粗糙度的识别程度,建立了一组随机表面模型.如图 12所示,随机表面为长宽各0.2m,高度在0~0.1m 范围内满足均匀分布的一组随机数,定义随机表面任意点的粗糙程度κij为(εr=8,μ=μ0,σ=104S/m):
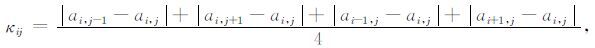
|
(5) |
|
图 12 三维随机表面正演模型 Fig. 12 3D model of random surface |
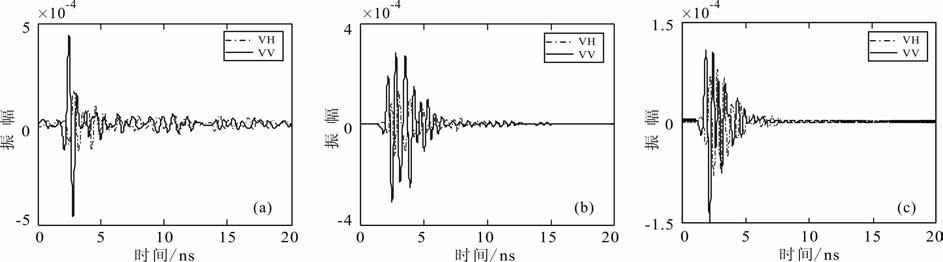
其中,ai,j为随机表面上任一点(i,j)的高度值.粗糙程度κij越大,说明该点和周边的高度差越大,表面越粗糙.图 13显示了随机表面上粗糙程度κ=1,3,6处的共极化和交叉极化响应.从图中可以看出粗糙程度κ 越大,共极化和交叉极化的响应振幅值越接近.
定义随机表面的整体粗糙程度为:
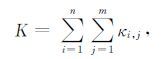
|
(6) |
其中,m和n分别为随机表面沿各自方向的网格节点数.
测线间距为0.05m,测点间距为0.01m,保持天线间距0.05m 不变,天线沿测线移动,分别计算每一测点处的共极化响应和交叉极化响应.定义平均振幅比Ψ 为:

|
(7) |
最大振幅比Φ 为:

|
(8) |
|
图 13 随机表面粗糙程度分别为1,3,6处的共极化和交叉极化响应(a)粗糙度为1的响应,(b)粗糙度为3的响应,(c)粗糙度为6的响应. Fig. 13 Signal of co-polarization and cross-polarization acquired above the point of random surface where roughness are 1 at (a),3 at (b) and 6 at (c) |
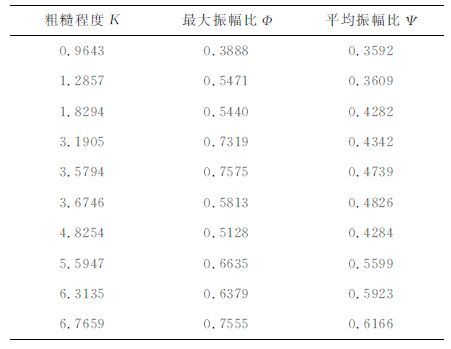
其中n为测线数,m为每条测线上的测点数,此处n=3,m=21.AVV,AVH 分别表示共极化和交叉极化响应振幅.表 2反映随机表面整体粗糙程度与振幅比(VH/VV)的关系,随着整体粗糙程度K的增大,平均振幅比Ψ 也增大,但最大振幅比Φ 没有表现出这种规律.因为整体粗糙程度反映的是表面粗糙程度的一个综合值,它不能清晰地反映局部情况,即整体粗糙程度小的表面有可能局部粗糙程度相对较大.平均振幅比是整个表面上振幅比的一个平均值,是一个综合值,所以它随着整体粗糙程度的增加而增加.而最大振幅比反映的是表面最粗糙的局部的情况,所以它不随着整体粗糙程度的增加而增加.
|
|
表 2 随机表面粗糙程度与振幅比(VH/W)关系 Table 2 Relationship between amplitude and roughness of random surface |
总结以上规律,发现表面的粗糙程度能影响到电磁波的共极化响应和交叉极化响应,并且表面越粗糙,电磁波的交叉极化响应和共极化响应振幅比越大.根据这个特点,我们可以通过振幅比来研究目标表面的粗糙程度.结合平均振幅比和最大振幅比两个参数,我们即可以研究目标体表面的整体粗糙程度,也可以研究目标体表面的最大粗糙程度.
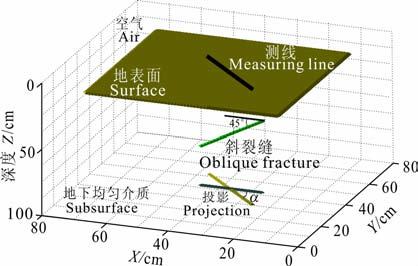
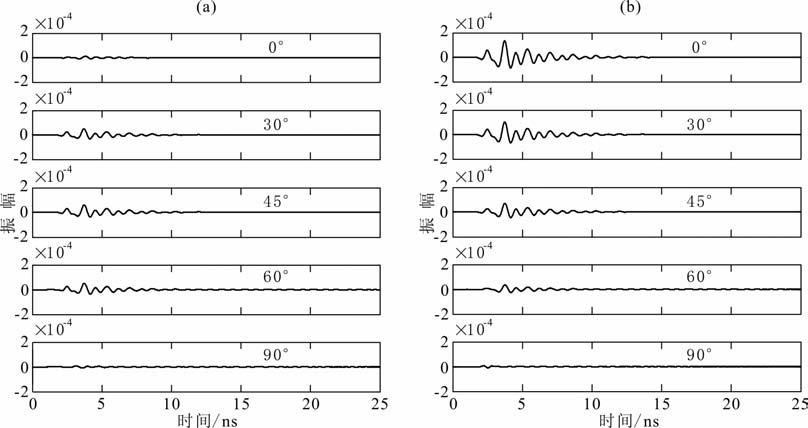
4.2 倾斜裂缝目标水利、公路等工程经常会出现各种原因形成的裂缝,对工程的强度和耐久造成影响[21~23].为研究全极化探地雷达对裂缝的响应情况,建立了斜裂缝模型(图 14),地下均匀介质(εr=8、μ=μ0、σ=5S/m)中有一倾斜裂缝,裂缝中介质为空气(εr=1、μ=μ0、σ=0).斜裂缝与水平面成45°角,斜裂缝长度为0.2m,测线与斜裂缝在水平面上投影为α 角.分别计算当α 角为0°、30°、45°、60°、90°时,全极化探地雷达的交叉极化响应和共极化响应,图 15(a,b)分别显示了斜裂缝中点处自激自收的交叉极化响应信号和共极化响应信号.从图中可以看出,交叉极化响应振幅随着角度的增加先增大后减小,在45°时达到最大,表现出以45°对称的规律.共极化响应振幅随着角度的增加不断减小,在90°达到了最小.0°时交叉极化响应振幅很小,共极化响应振幅很大.45°时交叉极化和共极化响应振幅基本相等.90°时交叉极化和共极化响应振幅都很小.
|
图 14 三维斜裂缝正演模型 Fig. 14 3D model of oblique fracture |
|
图 15 三维斜裂缝随角度变化的交叉极化响应(a)和共极化响应(b) Fig. 15 Signals of cross-polarization (a) and co-polarization (b) acquired above the oblique fracturewith the trend angle,0°,30°,45°,60°,90° |
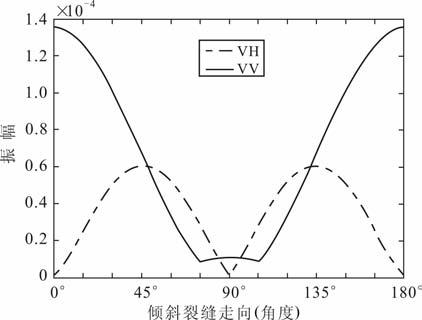
为了进一步研究共极化和交叉极化响应与斜裂缝走向之间的关系,我们每5°计算一组共极化和交叉极化响应,并提取最大响应振幅,将此振幅与走向角的关系显示在图 16 中.从中可以看出,交叉极化最大响应振幅表现出以90°和45°为对称轴的规律,而共极化最大响应振幅仅表现出以90°为对称轴的规律.在0°~ 45°、135°~ 180°以及90°附近共极化最大响应振幅要强于交叉极化响应振幅.而在其他角度,交叉极化最大响应振幅强于共极化最大响应振幅.这表明通过比较共极化最大响应和交叉极化最大响应振幅值的大小,可以判断斜裂缝的走向.
|
图 16 斜裂缝的共极化和交叉极化响应最大振幅与走向角的关系图 Fig. 16 The relationship between strike angel and the maximum amplitude of the cross-polarization and co-polarization signals |
本文通过水平正交双方向同时接收获取全极化信息,构建了基于时域有限差分法的全极化探地雷达正演模拟方法.该方法针对金属板和角反射器目标的正演模拟与实验室的物理测试取得了一致的共极化和交叉极化响应信息,说明此方法可以有效地模拟计算全极化探地雷达.正演模拟计算和实验室实验结果均反映出,交叉极化响应和共极化响应信息的结合有助于对目标的方位取向、结构组成等属性进行识别判断,在火山岩油气藏裂隙的勘探和评价中有潜在的应用价值.
| [1] | Zhou Zheng-Shu, Sato Motoyuki. Ground-based polarimetric SAR systems for environment studies. Antennas and Propagation Society International Symposium IEEE , 2003, 1: 202-205. |
| [2] | Zhou Zheng-Shu, Boerner Wolfgang-Martin, Sato Motoyuki. Development of a ground-based polarimetric broadband SAR system for noninvasive ground-truth validation in vegetation monitoring. IEEE Transactions on Geosciences and Remote Sensing , 2004, 42(9): 1803-1810. DOI:10.1109/TGRS.2004.832248 |
| [3] | Kovalenko V, Yarovoy A, Ligthart L P. Polarimetric feature fusion in GPR for Landmine detection. Geoscience and Remote Sensing Symposium,IGARSS 2007. IEEE International, July, 2007. 30-33 |
| [4] | 仝传雪, 刘四新, 王春辉. 时域有限差分(FDTD)模拟探地雷达极化测量. 吉林大学学报:地球科学版 , 2006, 36(Suppl.): 201–205. Tong C X, Liu S X, Wang C H. The simulation of GPR polarization measurement with Finite-Difference Time-Domain (FDTD) method. Journal of Jilin University: Earth Science Edition (in Chinese) , 2006, 36(Suppl.): 201-205. |
| [5] | Roberts R L, Daniels J J. Modeling near field GPR in three dimensions using the FDTD method. Geophysics , 1997, 62(4): 1114-1126. DOI:10.1190/1.1444212 |
| [6] | Jiao Yuren, George A, McMechan, Elena Pettinelli. In situ 2-D and 3-D measurements of radiation patterns of half-wave dipole GPR antennas. Journal of Applied Geophysics , 2000, 43: 69-89. DOI:10.1016/S0926-9851(99)00048-8 |
| [7] | 于继军.地下三维目标电磁散射的计算[硕士论文].北京:中国科学院研究生院(电子学研究所),2005 Yu J J. Research on scattering from 3-D targets in the subsurface [Master's thesis] (in Chinese).Beijing: Graduate University of Chinese Academy of Sciences (Institute of Electronics), 2005 http://cdmd.cnki.com.cn/Article/CDMD-80137-2006015177.htm |
| [8] | 冯德山, 戴前伟, 何继善, 等. 探地雷达GPR正演模拟的时域有限差分实现. 地球物理学进展 , 2006, 21(2): 630–636. Feng D S, Dai Q W, He J S, et al. Finite difference time domain method of GPR forward simulation. Progress in Geophysics (in Chinese) , 2006, 21(2): 630-636. |
| [9] | 张晓燕.地下目标电磁散射的时域有限差分计算[博士论文].北京:中国科学院研究生院(电子学研究所),2007 Zhang X Y. FDTD computation of scattering by buried objects [Doctor's thesis] (in Chinese). Beijing: Graduate University of Chinese Academy of Sciences (Institute of Electronics), 2007 |
| [10] | 杨利霞.复杂介质电磁散射的FDTD算法及其相关技术研究[博士论文]. 西安:西安电子科技大学,2006 Yang L X. Study of FDTD algorithm of electromagnetic scattering by complex media and related techniques [Doctor's thesis] (in Chinese).Xian: XIDIAN University, 2006 http://cdmd.cnki.com.cn/Article/CDMD-10701-2007049528.htm |
| [11] | 葛德彪, 闫玉波. 电磁波时域有限差分方法(第二版). 西安: 西安电子科技大学出版社, 2005 . Ge D B, Yan Y B. Finite-Difference Time-Domain Method for Electromagnetic Waves (in Chinese). Xi'an: XIDIAN University Press, 2005 . |
| [12] | 赵海波, 王秀明, 王东. 完全匹配层吸收边界在孔隙介质弹性波模拟中的应用. 地球物理学报 , 2007, 50(2): 581–591. Zhao H B, Wang X M, Wang D. Applications of the boundary absorption using a perfectly matched layer for elastic wave simulation in poroelastic media. Chinese J. Geophys. (in Chinese) , 2007, 50(2): 581-591. |
| [13] | Radzevicius S H, Chen C-C, Peters L, et al. Near-field radiation dynamics through FDTD modeling. Jour. Applied Geoph , 2003, 52: 75-91. |
| [14] | 冯德山, 陈承申, 戴前伟. 基于UPML边界条件的交替方向隐式有限差分法GPR全波场数值模拟. 地球物理学报 , 2010, 53(10): 2484–2496. Feng D S, Chen C S, Dai Q W. GPR numerical simulation of full wave field based on UPML boundary condition of ADI-FDTD. Chinese J. Geophys. (in Chinese) , 2010, 53(10): 2484-2496. |
| [15] | 刘四新, 曾昭发. 频散介质中地质雷达波传播的数值模拟. 地球物理学报 , 2007, 50(1): 320–326. Liu S X, Zeng Z F. Numerical simulation for ground penetrating radar wave propagation in the dispersive medium. Chinese J. Geophys. (in Chinese) , 2007, 50(1): 320-326. |
| [16] | Roger L Roberts, Jeffrey J Daniels. Modeling near-field GPR in three dimensions using the FDTD method. Geophysics , 1994, 62: 1114-1126. |
| [17] | 李丽丽, 冯晅, 鹿琪, 等. 极化步频探地雷达系统初步研究. 吉林大学学报:地球科学版 , 2008, 38(Supppl.): 150–152. Li L L, Feng X, Lu Q, et al. Preliminary study on polarization step frequency radar systems. Journal of Jilin University (Earth Science Edition) (in Chinese) , 2008, 38(Supppl.): 150-152. |
| [18] | Roberts R L, Daniels J J. Analysis of GPR polarization phenomena. Journal of Environmental and Engineering Geophysics , 1996, 1(2): 139-157. DOI:10.4133/JEEG1.2.139 |
| [19] | 胡祥云, 杨迪坤, 刘少华, 等. 环境与工程地球物理的发展趋势. 地球物理学进展 , 2006, 21(2): 598–604. Hu X Y, Yang D K, Liu S H, et al. The developing trends of environmental and engineering geophysics. Progress in Geophysics (in Chinese) , 2006, 21(2): 598-604. |
| [20] | 冯德山, 戴前伟. 高速公路路面厚度探地雷达检测. 地球物理学进展 , 2008, 23(1): 289–294. Feng D S, Dai Q W. Application of ground penetrating radar in the survey of the pavement thickness in highway. Progress in Geophysics (in Chinese) , 2008, 23(1): 289-294. |
| [21] | Guy Serbin T, Dani Or. Ground-penetrating radar measurement of crop and surface water content dynamics. Remote Sensing of Environment , 2005, 96: 119-134. DOI:10.1016/j.rse.2005.01.018 |
| [22] | Soon Jee Seol, Jung-Ho Kim. Finding the strike direction of fractures using GPR. Geophysical Prospecting , 2001, 49: 300-308. DOI:10.1046/j.1365-2478.2001.00262.x |
| [23] | Stanley J, Radzevicius, Jeffrey J Daniels. Ground penetrating radar polarization and scattering from cylinders. Journal of Applied Geophysics , 2000, 45: 111-125. DOI:10.1016/S0926-9851(00)00023-9 |
 2011, Vol. 54
2011, Vol. 54