2. 吉林师范大学凝聚态物理与材料科学研究所,四平 136000
2. Institute of Condensed Matter Physics and Materials Science, Jilin Normal University, Siping 136000, China
P-SV 转换波数据处理中共转换点道集的抽取和叠加是一个重要的步骤,也是与常规P 波数据处理的一个最主要的差别[1].同时接收函数阵列成像最为普遍的方法是共转换点偏移叠加[2, 3].转换点位置的计算是转换波道集的抽取和叠加中的一个关键问题,也是一个难题[4~9].一些学者通过对转换波转换点坐标方程的近似估计,获得了几种近似计算转换波转换点位置的公式[10~12].另外一些研究从转换波的反射几何学的角度出发,获得了几种用迭代逼近算法近似计算转换波转换点位置的方法[13~15].Schneider根据偏移距、横纵波速度和P-SV 转换波走时给出转换波转换点位置的解析解[16].
在均匀介质水平反射层情况下,Fromm 等[17]、许士勇等[18]、Dai[19]分别给出了计算转换点的近似方法.Tessmer和Behle[20]、Taylor[21]、苑春方[22, 23]、Zhong[24]等分别给出了水平单层介质中P-SV 转换波转换点坐标的解析解.在水平层状各向同性介质情况下,Thomsen[25]、陈雨红[26]、Chung[27]等给出了近似计算转换点的方法.在VⅡ介质情况下,一些学者[25, 28~30] 提出了近似的方法.Slawinski 和Margrave[31]研究了速度随深度线性变化情况下的转换点计算方法.在均匀介质倾斜界面情况下,YuanChunfang[32]、Alfredo Tada Guarin[33]、Chang[34]等分别给出了P-SV 转换波转换点坐标的解析解.在多个平行倾斜界面情况下,Gisa[35]研究了一种近似的方法.而对于多层任意倾斜层状介质的情况下P-SV转换波转换点坐标的计算,目前还没有进行详细研究.
本文通过搜索最符合Snell定律的入射角和反射角来确定最佳的P-SV 转换波转换点位置的方式,来研究多层倾斜层状介质中的P-SV 转换波转换点的坐标.
2 最佳角度搜索法 2.1 均匀介质倾斜反射层 2.1.1 原 理对于均匀介质倾斜反射层模型,我们选取坐标系如图 1,炮点S为坐标原点,X轴指向接收点R方向,Z方向垂直向下.反射界面倾角为θ,倾向为X轴正方向时θ 为正值,反之为负值.z0 是炮点正下方界面深度.接收点R深度为0,炮检距为h.

|
图 1 P-SV波在倾斜单层介质中的传播示意图 Fig. 1 Source-receiver geometry for a P-SV wave in a dipping bed model |
如图 1所示,在反射界面上定义任意一点F,其坐标为(x,z).G点是F点在X轴上的投影,其坐标为(x,0),所以SG的距离为x,GR的距离为h-x.此时,
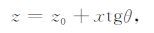
|
(1) |
定义SF和FG的夹角为α,GF和FR的夹角为β,均为正值.此时,
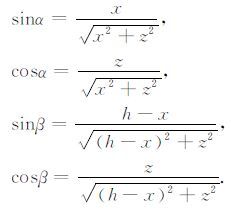
|
(2) |
定义一个反射函数f(x)为
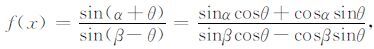
|
(3) |
再在反射函数的基础上定义误差函数e(x)为
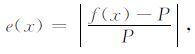
|
(4) |
式中,P为纵横波速度比:P=VP/VS.将(2)式和(3)式代入(4)式,可得
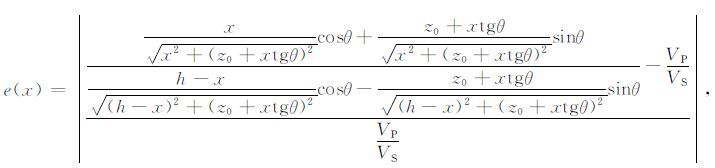
|
(5) |
当界面水平,即θ 角为0°时,可得

|
(6) |
如果F点为P-SV 转换波转换点,则α+θ 为入射角,β-θ 为反射角.根据Snell定律,反射函数f(x)应该等于纵横波速度比P,此时误差函数e(x)为0.所以当F点越接近P-SV 转换波转换点时,误差函数e(x)应该越小.根据这一原理,我们使用公式(4)或公式(5),通过搜索误差e(x)极小值处所对应的α 角和β 角来确定P-SV 转换波的最佳转换点.
2.1.2 最佳转换点搜索范围此算法也和其他计算转换点位置算法[7, 8]一样,需要预知倾斜反射界面的倾角θ 和深度z0,以及纵横波速度比VP/VS.网格间距Δx是用来将反射界面均匀网格化,以便计算机进行数值计算,它的选取将影响到转换波转换点的计算精度.因为P 波的速度总是大于SV 波的速度,所以根据Snell定律P-SV 转换波转换点的位置一定比P-P 反射波反射点的位置更加靠近接收点.又因为转换波转换点的位置一定不会越过接收点R在反射界面上投影点R′的位置,所以转换波转换点的x坐标应该在P-P 反射波反射点的x坐标xs 和投影点R′的x坐标xe之间.如图 2所示,接收点R正下方界面深度为z0+htgθ,则接收点R在反射界面上投影点R′的x坐标xe 为
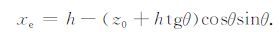
|
(7) |
|
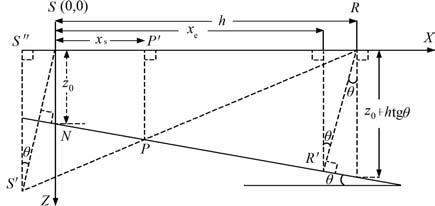
图 2 P-SV 转换波转换点计算范围(xs,xe)示意图 Fig. 2 Computing range,between xs and xe,of P-SV conversion point |
图 2中,S′是炮点的虚震源,S″是S′ 在X轴上的投影,S′R与反射界面的交点P则是P-P 反射波反射点,P′是P点在X轴上的投影,所以
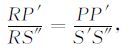
|
其中,PP′=z0+xstgθ,S′S″=2z0cosθcosθ,RP′=h-xs,RS″ =h+2z0cosθsinθ 代入上式得
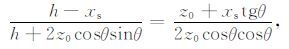
|
整理得

|
(8) |
根据(7)式和(8)式,我们能够确定转换波转换点的计算范围[xs,xe].
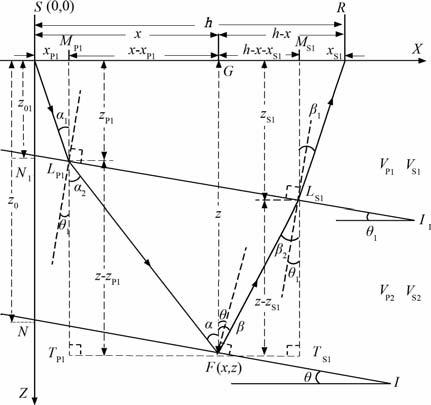
2.2 多层倾斜层状介质我们以双层倾斜层状介质中P-SV 转换波转换点的计算为例来说明多层倾斜层状介质中的情况.如图 3所示,炮点S为坐标原点,X轴指向接收点R方向,Z方向垂直向下.I是底部反射界面,I1 是地下第一个界面,θ是底部反射界面的倾角,θ1 是地下第一个界面的倾角,倾向为X轴正方向时倾角为正值,反之为负值.接收点R深度为0,炮检距为h.z0是炮点正下方底界面深度,z01是炮点正下方第一界面深度.
|
图 3 P-SV波在双层倾斜层状介质中的传播示意图 Fig. 3 Source-receiver geometry for a P-SV wave in a layered model with two dipping interfaces |
与均匀介质倾斜反射层情况类似,我们在反射界面上定义任意一点F,其坐标为(x,z).G点是F点在X轴上的投影,其坐标为(x,0),所以SG的距离为x,GR的距离为h-x,z=z0 +xtgθ.为了计算转换波转换点位置,我们首先计算入射P 波和反射SV 波在界面上的折射点位置.
2.2.1 最佳入射P波折射点如图 3 所示,首先在界面I1 上定义任意一点LP1,其坐标为(xP1,zP1),MP1是LP1在X轴上的投影点,此时
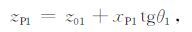
|
(9) |
同时,定义SLP1和LP1MP1的夹角为α1,LP1F和垂线的夹角为α2,均为正值.此时
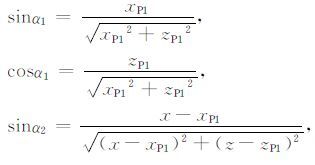
|
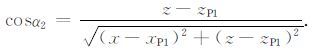
|
(10) |
定义一个函数fP1(xP1)为
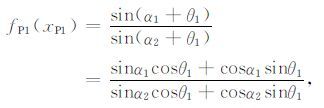
|
(11) |
再在以上函数的基础上定义误差函数eP1(xP1)为
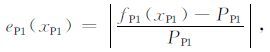
|
(12) |
式中,PP1 为第一层和第二层纵波速度比:PP1 =VP1/VP2.
如果LP1点为P波折射点,则α1+θ1 为入射角,α2+θ1 为折射角.根据Snell定律,函数fP1(xP1)应该等于第一层和第二层纵波速度比PP1,此时误差函数eP1(xP1)为0.所以当LP1点越接近P 波折射点时,误差函数eP1(xP1)应该越小.根据这一原理,我们使用公式(12),通过搜索误差eP1(xP1)极小值处所对应的α1 角和α2 角来确定入射P 波的最佳折射点.
2.2.2 最佳反射SV 波折射点同理,我们首先在界面I1 上定义任意一点LS1,其坐标为(h-xS1,zS1),MS1是LS1在X轴上的投影点,xS1是MS1点和R点之间的距离,此时
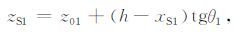
|
(13) |
同时,定义RLS1和LS1MS1的夹角为β1,LS1F和垂线的夹角为β2,均为正值.此时,
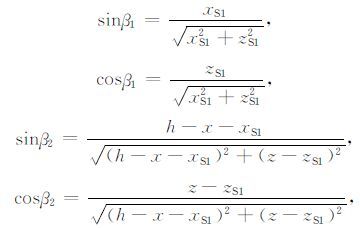
|
(14) |
定义一个函数fS1(xS1)为
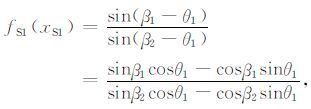
|
(15) |
再在以上函数的基础上定义误差函数eS1(xS1)为
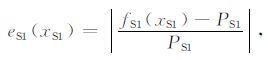
|
(16) |
式中,PS1 为第一层和第二层横波速度比:PS1 =VS1/VS2.
如果LS1点为SV 波折射点,则β2 -θ1 为入射角,β1-θ1 为折射角.根据Snell定律,函数fS1(xS1)应该等于第一层和第二层横波速度比PS1,此时误差函数eS1(xS1)为0.所以当LS1点越接近SV 波折射点时,误差函数eS1 (xS1)应该越小.根据这一原理,我们使用公式(16),通过搜索误差eS1(xS1)极小值处所对应的β1 角和β2 角来确定反射SV 波的最佳折射点.
2.2.3 最佳P-SV 转换点如图 3所示,定义LP1F和FG的夹角为α,GF和FLS1的夹角为β,可得
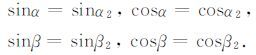
|
(17) |
将(17)式代入(3)式再代入(4)式,我们就可以获得误差函数e(x),但是此误差函数式中的P为最底层的纵横波速度比:P=VP2/VS2.同理,我们使用公式(4),通过搜索误差e(x)极小值处所对应的α角和β 角来确定P-SV 转换波的最佳转换点.
2.2.4 最佳折射点搜索范围如图 4所示,因为折射点LP1的位置一定在炮点S在界面I1 上投影点S1′ 和转换波转换点在界面I1 上投影点F1′之间,所以折射点LP1点计算的初始x坐标xP1s为炮点S 在界面I1 上投影点S1′的x坐标,
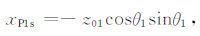
|
(18) |
折射点LP1点计算的终止x坐标xP1e为点F在界面I1 上投影点F1′的x坐标,
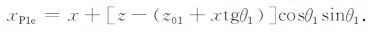
|
(19) |
|
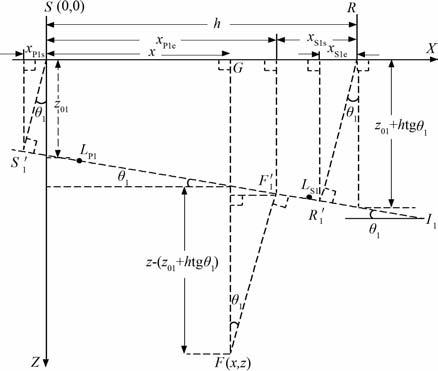
图 4 P波、SV波折射点计算范围示意图 Fig. 4 Computing range for transmission point of P wave and SV wave,respectively |
如图 4所示,因为折射点LS1的位置一定在转换波转换点在界面I1 上投影点F1′和接收点R在界面I1 上投影点R1′之间,所以折射点LS1点计算的初始值xS1s为点F在界面I1 上投影点F1′在X轴上的投影点与R点之间的距离,
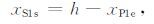
|
(20) |
折射点LS1点计算的终止值xS1e为接收点R在界面I1 上投影点R1′ 在X轴上的投影点与R点之间的距离,
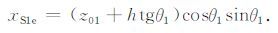
|
(21) |
要将双层倾斜层状介质情况拓展到多层倾斜层状介质情况,只须分别在计算最佳入射P 波折射点模块中添加针对其他界面的最佳P 波折射点模块,和在计算最佳反射SV 波折射点模块中添加针对其他界面的最佳SV 波折射点模块.这样本算法即可顺序计算每个折射界面上的折射点位置并最终确定转换波转换点的位置,并且通过折线连接入射波折射点、转换点和反射波折射点,我们还可以获得P-SV 波的传播路径.
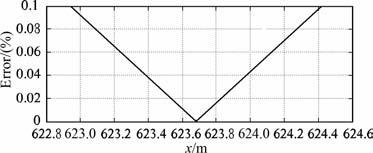
3 模型计算 3.1 均匀介质倾斜反射层我们设计了一个均匀介质倾斜反射层模型,反射界面倾角为30°,倾向为X轴正方向,炮点正下方界面深度为1000m,炮检距为2500m,纵横波速度比为2.设定网格间距Δx为0.01 m,根据公式(5)进行计算,获得误差函数e(x)曲线,如图 5所示.误差函数e(x)极小值所对应的x坐标为623.68m,此时误差e(x)为0.00046143%.再根据公式(1)确定z坐标为1360.08m.所以此模型下,转换波转换点的坐标为(623.68m,1360.08m).
|
图 5 均匀介质倾斜反射层模型误差函数e(x)曲线 Fig. 5 Error curve for a dipping bed |
为了研究网格间距对精度的影响,计算了不同网格间距情况下的误差,如图 6 所示.整体趋势上,误差随着网格间距的减小而减小,所以通常采用较小的网格间距,能获得较高的计算精度.从细节处看,曲线呈现一种有规律的波动,在某些较大网格间距情况下也能获得较高的计算精度,这说明计算精度并不完全是由网格间距所控制.实际上计算精度是与网格节点和转换点之间的最小距离有关,当某个节点正好处在转换点位置时,计算误差应该为0,而不论此时的网格间距为多少.所以网格间距只是控制了这个最小距离的波动范围,例如当网格间距为2时,最小距离的波动范围为0~2,而当网格间距为0.2 时,最小距离的波动范围为0~0.2.所以从整体趋势上,网格间距的减小将引起波动范围的最大值减小,从而使误差减小;但是从细节处,误差在波动范围内震荡,呈现数值上的波动.

|
图 6 均匀介质倾斜反射层模型转换点 计算误差与网格间距关系图 Fig. 6 The relation curve between computation error and gridding space for a dipping bed |
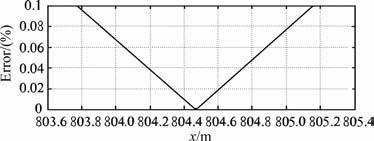
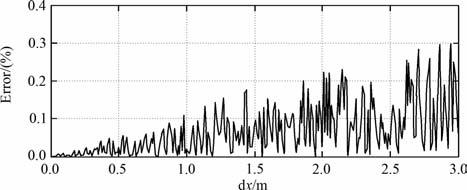
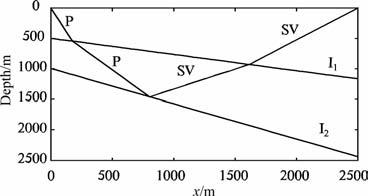
我们设计了一个双层倾斜层状介质模型,底部反射界面的倾角为30°,地下第一个界面的倾角为15°,倾向为X轴正方向,炮点正下方底界面深度为1000m,炮点正下方第一界面深度为500m,炮检距为2500m,第一层纵波速度为2000m/s,横波速度为1000m/s,第二层纵波速度为2800 m/s,横波速度为1400m/s.设定网格间距Δx为0.01 m,获得误差函数e(x)曲线,如图 7 所示.误差函数e(x)极小值所对应的x坐标为804.47m,此时误差e(x)为0.00037084%.再根据公式(1)确定z坐标为1464.46m.所以此模型下,转换波转换点的坐标为(804.47m,1464.46 m).同上,也计算了不同网格间距情况下的误差曲线,如图 8所示,它所表现出的规律与在均匀介质倾斜反射层模型中误差对网格间距曲线所表现的规律一致,只是震荡更加剧烈.计算过程中本算法可顺序计算每个折射界面上的折射点位置,通过折线连接入射波折射点、转换点和反射波折射点,我们可以获得P-SV波的传播路径,如图 9所示.
|
图 7 双层倾斜层状介质模型误差函数e(x)曲线 Fig. 7 Error curve for a double-dipping layered model |
|
图 8 双层倾斜层状介质模型转换点 计算误差与网格间距关系图 Fig. 8 The relation curve between computation error and gridding space for a double-dipping layered model |
|
图 9 双层倾斜层状介质模型中计算出的P-SV波的传播路径 Fig. 9 The P-SV ray path in the double-dipping layered model |
本文提出了求取P-SV 转换波转换点位置的最佳角度搜索法,该方法不仅可以求取均匀介质倾斜反射层情况下的转换波转换点位置,而且可以求取多层倾斜层状介质情况下的转换波转换点位置,并且该方法还能在获得转换点位置的同时给出P-SV波的传播路径.通过模型计算验证,该方法能获得很高的计算精度,其计算精度可以通过调节网格间距来进行控制.
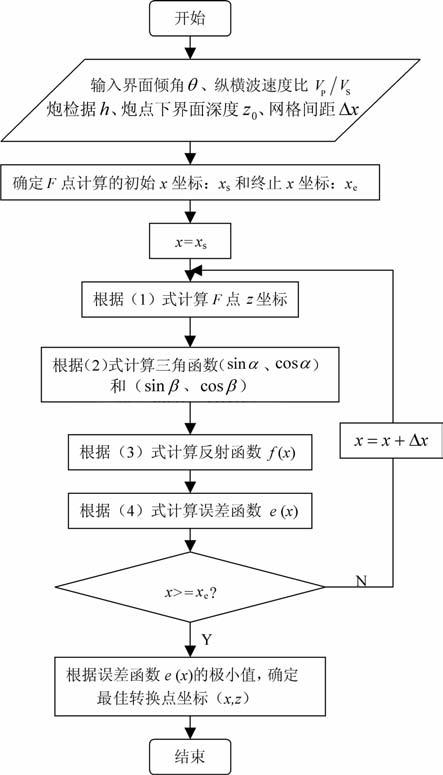
附录A 倾斜单层介质中计算P-SV 转换波转换点处理流程根据倾斜单层介质中计算P-SV 转换波转换点原理,我们设计了针对均匀介质倾斜反射层情况下,计算P-SV 转换波转换点的处理流程,如附图 1 所示.其中,网格间距Δx是用来将反射界面均匀网格化,以便计算机进行数值计算,它的选取将影响到转换波转换点的计算精度.最终我们能获得误差函数e(x).通过搜索误差函数e(x)极小值所对应的x坐标,我们就能够确定最佳转换点的x坐标,再使用公式(1)确定z坐标.
|
图 1 倾斜单层介质中计算P-SV转换波转换点处理流程 Fig. 1 Processing procedure for estimation of optimal P-SV conversion point in a dipping layered medium |
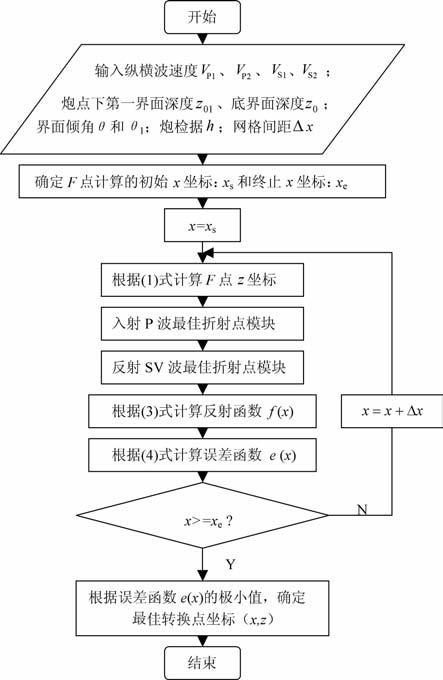
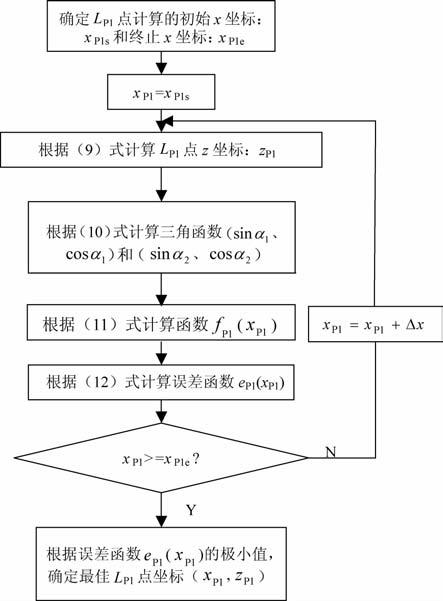
根据多层倾斜层状介质中计算P-SV 转换波转换点原理,我们设计了针对双层倾斜层状介质情况下,计算P-SV 转换波转换点的处理流程,如附图 2所示.与均匀介质倾斜反射层情况下计算P-SV 转换波转换点的处理流程(附图 1)对比,能够发现此流程只是添加了两个计算折射点的模块,它们分别是计算入射P波最佳折射点模块(附图 3)和计算反射SV 波最佳折射点模块(附图 4).因为这两个计算模块和P-SV 转换波转换点的处理流程(附图 1)都是使用搜索最佳角度的思想,所以比较就会发现,它们彼此非常相似.
|
图 2 双层倾斜层状介质中计算P-SV转换波转换点处理流程 Fig. 2 Processing procedure for estimation of optimal P-SV conversion point in a layered model with two dipping interfaces |
|
图 3 人射P波最佳折射点处理模块 Fig. 3 Processing procedure for estimation of optimal P wave transmission point |
|
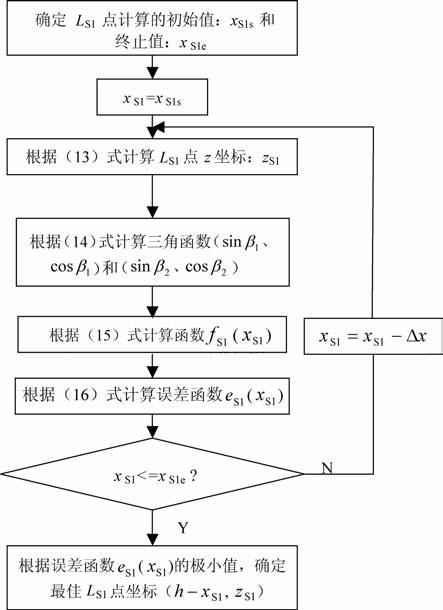
图 4 反射SV波最佳折射点处理模块 Fig. 4 Processing procedure for estimation of optimal SV wave transmission point |
| [1] | 郭向宇, 凌云, 魏修成. PS 转换波共转换点的几种计算方法及实际应用. 石油物探 , 2002, 41(2): 141–143. Guo X Y, Ling Y, Wei X C. Calculation procedures for common conversion points of PS converted waves and their application. Geophysical Prospecting for Petroleum (in Chinese) , 2002, 41(2): 141-143. |
| [2] | 吴庆举, 李永华, 张瑞青, 等. 接收函数的克希霍夫2 D偏移方法. 地球物理学报 , 2007, 50(2): 539–545. Wu Q J, Li Y H, Zhang R Q, et al. 2D Kirchhoff migration for receiver function. Chinese J. Geophys. (in Chinese) , 2007, 50(2): 539-545. DOI:10.1002/cjg2.v50.2 |
| [3] | 王红落, 常旭, 陈传仁. 基于波动方程有限差分算法的接收函数正演与偏移. 地球物理学报 , 2005, 48(2): 415–422. Wang H L, Chang X, Chen C R. Receiver function forward modeling and migration based on wave-equation finite difference method. Chinese J. Geophys. (in Chinese) , 2005, 48(2): 415-422. |
| [4] | 严寿民, 陈静. P-SV转换波的一种处理方法——叠前抽道集法. 地球物理学进展 , 1995, 10(2): 57–66. Yan S M, Chen J. A processing method of P-SV wave prestack trace gathering method. Progress in Geophysics (in Chinese) , 1995, 10(2): 57-66. |
| [5] | 谢飞, 常旭, 刘伊克. 火山岩地震屏蔽层的转换波叠前时间偏移成像. 地球物理学报 , 2008, 51(6): 1899–1908. Xie F, Chang X, Liu Y K. Converted-wave pre-stack time migration in volcanic area. Chinese J. Geophys. (in Chinese) , 2008, 51(6): 1899-1908. |
| [6] | 石建新, 王延光, 毕丽飞, 等. 多分量地震资料处理解释技术研究. 地球物理学进展 , 2006, 21(2): 505–511. Shi J X, Wang Y G, Bi L F, et al. The process-interpretation technique of multi-component seismic data. Progress in Geophysics (in Chinese) , 2006, 21(2): 505-511. |
| [7] | 王立明, 李庆春. 选择相关法提高转换波速度分析精度. 地球物理学进展 , 2006, 21(4): 1213–1220. Wang L M, Li Q C. Improving the accuracy of converted-wave velocity analysis with selected-correlation method. Progress in Geophysics (in Chinese) , 2006, 21(4): 1213-1220. |
| [8] | 李天成, 牛滨华, 孙春岩, 等. VTI介质中P-SV波转换点与各向异性参数关系. 地球物理学进展 , 2007, 22(5): 1522–1526. Li T C, Niu B H, Sun C Y, et al. The relationship of VTI media P-SV wave converted point and anisotropy parameters. Progress in Geophysics (in Chinese) , 2007, 22(5): 1522-1526. |
| [9] | 杨文采, 朱光明, 杨振华, 等. 中国大陆科学钻探孔区的数字三分量反射地震调查. 地球物理学报 , 2007, 50(3): 780–790. Yang W C, Zhu G M, Yang Z H, et al. Three-component seismic profiling at the Chinese Continental Scientific Drilling Site. Chinese J. Geophys. (in Chinese) , 2007, 50(3): 780-790. |
| [10] | 赵爱华, 张中杰. 三维复杂介质中转换波走时快速计算. 地球物理学报 , 2004, 47(4): 702–707. Zhao A H, Zhang Z J. Fast calculation of converted wave traveltime in 3-D complex media. Chinese J. Geophys. (in Chinese) , 2004, 47(4): 702-707. |
| [11] | 马在田, 曹景忠, 王家林, 等. 计算地球物理学概论. 上海: 同济大学出版社, 1987 . Ma Z T, Cao J Z, Wang J L, et al. Survey of Computational Geophysics (in Chinese). Shanghai: Tongji Univ. Press, 1987 . |
| [12] | 张中杰. 多分量地震资料各向异性处理与解释方法. 哈尔滨: 黑龙江教育出版社, 2002 . Zhang Z J. Multi-component Seismic Data Processing and Interpretation for Anisotropy (in Chinese). Harbin: Heilongjiang Education Press, 2002 . |
| [13] | 张耀辉. 关于倾斜界面转换点的确定. 石油地球物理勘探 , 1993, 28(6): 752–760. Zhang Y H. Determination of conversion points in a slant interface. Oil Geophysical Prospecting (in Chinese) , 1993, 28(6): 752-760. |
| [14] | 周竹生, 王卫华. 一种快速、高精度的共转换点轨迹计算方法. 石油地球物理勘探 , 1993, 28(1): 37–45. Zhou Z S, Wang W H. A method for fast and accurately computing the common conversion point locus. Oil Geophysical Prospecting (in Chinese) , 1993, 28(1): 37-45. |
| [15] | 傅旦丹, 朱宏彰, 何汉漪. 一种确定转换点的算法及应用. 石油物探 , 2002, 41(1): 26–30. Fu D D, Zhu H Z, He H Y. A method for determination of conversion points and its application. Geophysical Prospecting for Petroleum (in Chinese) , 2002, 41(1): 26-30. |
| [16] | Schneider Jr W A. A simple, exact solution for the P-SV wave conversion point via prestack migration. Geophysics , 2002, 67(5): 1634. DOI:10.1190/1.1512810 |
| [17] | Fromm G, Krey T, Wiest B. Static and dynamic corrections, seismic shear waves. In: Dohr G ed. Handbook of Geophysical Exploration. Geophys. Press, 1985 |
| [18] | 许士勇, 马在田. 快速有效的转换波共转换点叠加技术. 地球物理学报 , 2002, 45(4): 557–568. Xu S Y, Ma Z T. A fast and efficient common conversion point stacking technique for converted waves. Chinese J. Geophys. (in Chinese) , 2002, 45(4): 557-568. |
| [19] | Dai H C. An approximation of the conversion-point of PS converted waves based on Newton's methods. EAGE 66th Conference & Exhibition, 2004. P026 |
| [20] | Tessmer G, Behle A. Common reflection point data stacking technique for converted waves. Geophysical Prospecting , 1988, 36(7): 671-688. DOI:10.1111/gpr.1988.36.issue-7 |
| [21] | Taylor Gary G. The point of P-S mode-converted reflection: an exact determination. Geophysics , 1989, 54(9): 1060-1063. |
| [22] | 苑春方, 彭苏萍, 杨良梁. 水平界面上P-SV 转换波转换点的精确解. 地球物理学报 , 2005, 48(5): 1179–1184. Yuan C F, Peng S P, Yang L L. An exact solution of the coordinate equation of the conversion point for P-SV converted waves at a horizontal reflector. Chinese J. Geophys. (in Chinese) , 2005, 48(5): 1179-1184. |
| [23] | 苑春方, 彭苏萍, 唐俐威, 等. 含有旅行时间的水平反射界面上P-SV转换波转换点坐标的唯一解析解. 地球物理学进展 , 2006, 21(4): 1127–1131. Yuan C F, Peng S P, Tang L W, et al. A unique solution with traveltime for the P-SV wave conversion point in a horizontal reflector. Progress in Geophysics (in Chinese) , 2006, 21(4): 1127-1131. |
| [24] | Zhong B S, Zhou X X, Liu X C, et al. A new strategy for CCP stacking. Geophysics , 1995, 60(2): 517-521. DOI:10.1190/1.1443788 |
| [25] | Thomsen Leon. Converted-wave reflection seismology over inhomogeneous, anisotropic media. Geophysics , 1999, 64(3): 678-690. DOI:10.1190/1.1444577 |
| [26] | 陈雨红, 魏修成. 垂向非均匀介质中转换波转换点计算. 地球物理学报 , 2007, 50(4): 1225–1231. Chen Y H, Wei X C. Conversion points of converted wave in vertical inhomogeneous media. Chinese J. Geophys. (in Chinese) , 2007, 50(4): 1225-1231. |
| [27] | Chung W Y, Corrigan D. Gathering mode-converted shear waves: a model study. 55th SEG Mtg, Expanded Abstracts, 1985. 602-604 |
| [28] | Li Xiang-Yang, Yuan Jianxin. Converted-wave moveout and conversion-point equations in layered VTI media : theory and applications. Journal of Applied Geophysics , 2003, 54: 297-318. DOI:10.1016/j.jappgeo.2003.02.001 |
| [29] | Yuan Jianxin. Analysis of four-component seafloor seismic data for seismic anisotropy [Ph. D. thesis]. Scotland: University of Edinburgh, 2001 |
| [30] | Traub Barbel M. Anisotropic parameter estimation from PP and PS waves in 4-component data [Ph. D. thesis]. Scotland: Unversity of Edinburgh, 2004 |
| [31] | Michael A Slawinski, Gray F Margrave. The P-SV conversion point in constant-gradient media. The University of Calgary, CREWES Research Report Vol(9) 1997. http://www.crewes.org/ForOurSponsors/ResearchReports/1997/1997-14.pdf |
| [32] | Yuan Chunfang, Peng Suping, Li Chunming. An exact solution of the conversion point for the converted waves from dipping reflector with homogeneous (isotropic) overburden. Geophysics , 2006, 71(1): T93-T97. |
| [33] | Alfredo Tada Guarin. On the calculation of P-SV conversion point for a dipping bed. Geophysics , 2006, 71(1): T13-T16. DOI:10.1190/1.2159060 |
| [34] | Chang Young-Fo, Tang Yi-Jun. The equation of conversion point for the converted wave on a dipping layer. 75th SEG Mtg, Expanded Abstracts, 2005.1007-1009 |
| [35] | Gisa Tessmer, Alfred Behle. Conversion points and traveltimes of converted waves in parallel dipping layeres. Geophysical Prospecting , 1991, 39: 387-405. DOI:10.1111/gpr.1991.39.issue-3 |
 2011, Vol. 54
2011, Vol. 54


