利用地球物理场(地磁场、重力场)的特征进行导航是近几年新兴的辅助导航方法,并已经发展成为导航领域的一个研究热点[1~3].在地球物理场辅助导航中,如何获取准确的地球位场数据库是实现位场导航的关键问题.位场向下延拓的积分迭代法[4, 5]作为一种解决位场大数据量、大深度向下延拓的有效方法,有望在构建不同高度位场数据库的过程中发挥重要作用.目前,该方法的收敛性问题已得到解决[6, 7];噪声对该方法的影响及解决方法也有详尽的分析[8, 9].
正则化方法是求解不适定反问题理论上最完备且行之有效的方法[10, 11].针对位场向下延拓的不适定性,安玉林和管志宁[12]根据正则化理论提出了一种滤除高频干扰的正则化稳定因子;梁锦文[13]比较分析了正则化方法位场向下延拓的四个频率响应公式的特点;Cooper[14] 用对比实验说明基于Tikhonov 正则化的向下延拓方法,既能最小化FFT 向下延拓产生的噪声误差,又能使向下延拓稳定并滤除原始数据中存在的噪声,但同时也指出,该向下延拓方法因需要矩阵求逆而不适合于大面积的位场数据延拓处理;王兴涛等[15, 16]分析了航空重力数据向下延拓的正则化算法,并对重力资料处理中常用的几种位场向下延拓方法进行了比较,得出正则化方法向下延拓效果最好的结论;陈龙伟等[17]采用正则化方法中的Landweber迭代法实现了地磁数据的向下延拓,并得到较好的延拓效果;郝燕玲等[18]基于Tikhonov正则化算法,对航空重力测量数据进行向下延拓,其仿真实验结果表明,该算法能够有效地抑制高频噪声和解决重力场向下延拓不稳定的问题.
本文首先从积分迭代法的迭代形式出发,基于Kirsch正则化子理论[19],推导了积分迭代法的正则化滤子函数,并由此证明积分迭代法是一种求解位场向下延拓不适定反问题的正则化方法,从而将积分迭代法归类到正则化方法,并为将该方法应用到其他领域的不适定反问题求解提供了理论依据.同时,针对积分迭代法迭代步长固定,导致迭代次数过多而影响其收敛速度的问题,提出该迭代法最优迭代步长的选择原理,最后,通过基于理论模型和实测数据的对比实验说明,最优迭代步长下的积分迭代法其收敛速度明显加快,延拓精度有所提高.
2 积分迭代法位场延拓原理及其正则性分析 2.1 位场向下延拓原理设z轴向下为正,场源位于z= h平面以下(h>0),若z=0观测平面上的位场f(x)为已知,则由f(x)求z=h平面上的位场数据g(x)称为位场的向下延拓[20]:
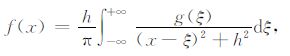
|
(1) |
令
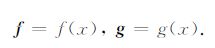
|
(2) |
并定义向上延拓线性积分算子K:g→f
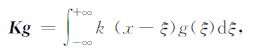
|
(3) |
其中,k(x-ξ)=h/π[(x-ξ)2+h2],则(1)式可表示成如下的第一类Fredholm 算子方程:
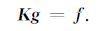
|
(4) |
位场向下延拓为一不适定反问题,方程(4)的求解一般是病态的,主要是方程的解不连续依赖于右端的数据,当右端的数据有误差时(这在实际运用中不可避免),其近似解与真解之间会产生很大的误差.
2.2 位场向上延拓算子的谱分析如何建立有效的正则化方法是不适定反问题研究的重要内容.通常的正则化方法有基于变分原理的Tikhonov正则化方法、各种迭代正则化方法、有限维近似和离散正则化方法等[11].Kirsch[19]用基于谱分析的方法讨论不适定反问题的正则化,通过引入正则化滤子函数来构造正则算子,从而提供了建立正则化方法的理论依据,每一种正则化滤子函数对应一种正则化方法.
设方程(4)右端实测带误差位场数据fδ 满足条件‖fδ -f‖ ≤δ(δ 为误差上限,δ>0),(μi,gi,fi)为算子K的一个奇异系统,由于Fredholm 算子一般为紧算子[11],则方程(4)在Picard定理下的唯一真解可表示为[19]
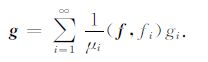
|
(5) |
由于i→ ∞ 时,μi→0,所以,当f存在误差时,这个唯一真解是不稳定的,可以通过与一个函数相乘来衰减1/μi的影响,从而构造正则化策略.
设紧算子K的奇异系统为(μi,gi,fi),如果函数q(α,μ)具有性质
(1) 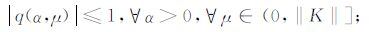
(2) 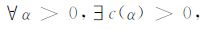
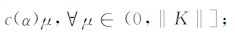
(3) 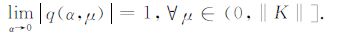
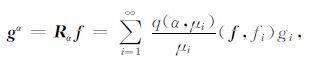
|
(6) |
其中,q(α,μ)定义为算子K的一个正则化滤子函数,α >0称为正则化参数.Krisch的正则化子理论就是通过构建函数q(α,μ),并证明q(α,μ)满足正则化滤子函数的三个条件来构造新的正则化方法.
2.3 积分迭代法的正则性分析文献[4]提出位场向下延拓的积分迭代法,即通过如下迭代式来获取向下延拓平面位场数据g的渐进精确值
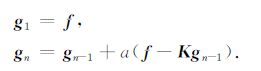
|
(7) |
n=2,3,4… 为迭代次数,gn为第n次迭代的g(x)近似值,a为迭代步长,一般取a=1.为便于分析,可构建如下不失一般性的积分迭代法迭代形式:
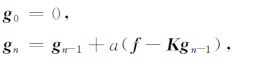
|
(8) |
n=1,2,3,…,则由数学归纳法

|
(9) |
应用算子K的奇异系统(μi,gi,fi),可得[19]
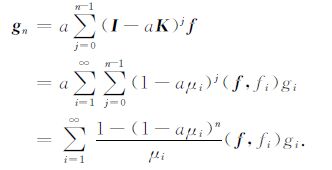
|
(10) |
对比(10)式和(6)式可得积分迭代法形式上对应的正则化滤子函数为

|
(11) |
下面证明q(a,μi)=1-(1-aμi)n满足2.2节正则化滤子函数需满足的三个条件:
首先,对任意0 <a≤ 1/‖K‖,由0 <μ ≤‖K‖,则q(α,μi)=1-(1-αμi)n显然满足第一个和第三个条件;
其次,由Bernoulli不等式:(1+x)n≥1+nx(x>-1,n为正整数),可知q(a,μi)= 1- (1-aμi)n≤anμi,令c(α)=anμi,即可证明q(a,μi)=1-(1-aμi)n也满足正则化滤子函数的第二个条件.
由此可见,积分迭代法的正则化滤子函数为1-(1-aμi)n,该迭代法是一种求解不适定反问题的正则化方法,其迭代步长a等价于正则化方法所谓的正则化参数α.
3 最优迭代步长的选择原理迭代步长a的选择对积分迭代法收敛性和收敛速度的影响是显而易见的.迭代式(8)中f-Kgn-1可以看成是迭代法第n次迭代时的迭代误差,而a的大小决定该迭代误差在第n+1次迭代过程中对误差进行修正的幅度;a过大,可能会使误差修正过多,导致迭代发散,而a过小,则误差修正幅度小,进而使收敛的速度变慢,导致迭代次数和运算时间增多.针对这个问题,我们提出最优迭代步长的选择原理.
首先,我们令固定步长积分迭代法的迭代步长a为随迭代次数n变化的变步长an,则得到变步长的积分迭代法迭代式(g0=0):
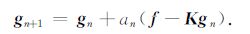
|
(12) |
如果我们定义该迭代法第n次迭代时的误差为en=f-Kgn,则其第n+1次迭代的误差:
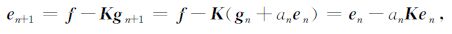
|
(13) |
令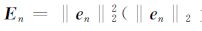
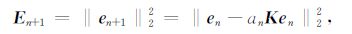
|
(14) |
可见,En+1 为迭代步长an的函数,我们要获得最小的第n+1步迭代时的误差En+1,可令
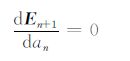
|
(15) |
求解方程(15),即可得第n次迭代的最优迭代步长an
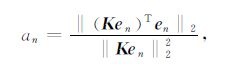
|
(16) |
T 代表转置.
结合上述分析及固定步长积分迭代法的迭代步骤[4, 5],最优迭代步长下积分迭代法向下延拓的迭代步骤可归纳为
(1) 以观测平面的位场值f作为向下延拓平面的位场初值g1;
(2) 将g1 向上延拓到观测平面,即Kg1,并计算观测位场值f与延拓值Kg1 的误差e1 =f-Kg1;
(3) 利用公式(16)式计算最优迭代步长a1,然后乘以误差e1 并与g1 相加来修正向下延拓平面的位场初值,即g1 +a1e1;
(4) 重复(2)、(3)步,直到误差|en|<ε(ε 为很小的数),即停止迭代.
4 数值试验及结果比较为验证第3节提出的最优迭代步长的选择对积分迭代法的改善,本文分别采用三维理论模型数据和三维实测数据进行数值试验.
4.1 理论模型试验采用文献[7]的双球体重力模型.两个球体的参数相同:剩余密度Δσ=1.0t/m3、半径r=0.5km、中心埋深1.8km、球心x坐标分别为10km 和15km、球心y坐标12.5km、z坐标向下为正,线数M和每线点数N同为512、点距Δx和线距Δy都为50m.
根据球体重力场公式[21]
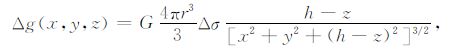
|
(17) |
计算得h=0m、h=500m、h=750m、h=1000m 平面处的重力数据.我们以h=0 m 平面处的重力数据为观测位场数据,然后分别用最优迭代步长和固定步长为1的积分迭代法将其向下延拓500 m(10倍点距)、750 m(15 倍点距)、1000 m(20 倍点距),并用得到的延拓值Δgc 与500m、750m、1000m 高度处的真实重力场值Δgt 采用公式[8]

|
(18) |
计算两种步长下积分迭代法向下延拓后对应的延拓误差Δgerr.
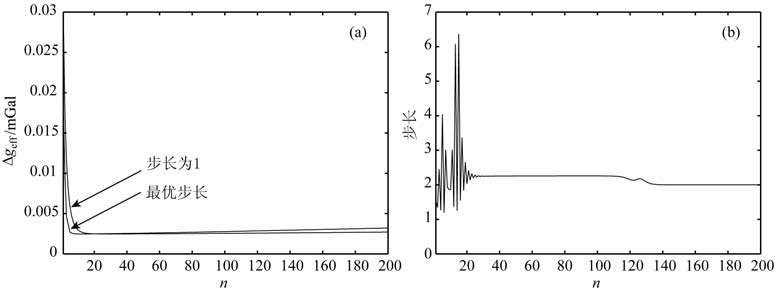
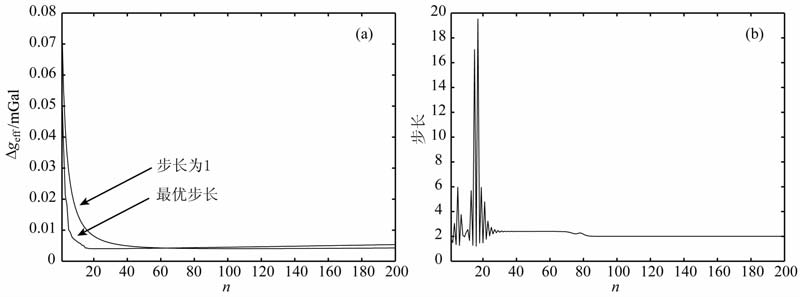
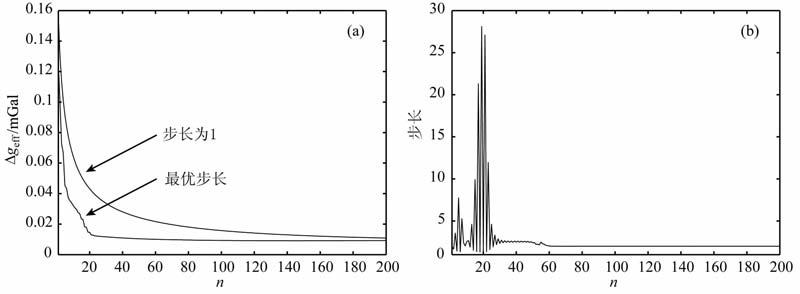
将h=0m 平面处的重力数据分别向下延拓三个深度后,最优迭代步长和固定步长积分迭代法各自的三个延拓误差Δgerr随迭代次数n的变化关系分别如图 1a、2a、3a所示;最优迭代步长随迭代次数的变化分别如图 1b、图 2b、图 3b 所示.可见:(1)最优迭代步长能够有效地减少积分迭代法收敛的迭代次数,加快迭代法的收敛速度;(2)三个延拓深度的每一最优迭代步长an都大于固定步长1,且an随迭代次数n增加的变化趋势一致,即前期表现为一震荡过程,并间或有较大震荡;(3)向下延拓的深度越深,最优迭代步长变化趋势最大震荡处的震荡幅度越大,但通过一定次数的迭代,迭代步长统一收敛到1.99左右,这样就能够保证最优迭代步长积分迭代法的收敛性.
|
图 1 向下延拓10倍点距 (a)最优步长和固定步长下的误差随迭代次数变化的关系;(b)最优迭代步长和迭代次数的关系. Fig. 1 Downward continuation 10 grid interval (a) Relationship between errors and iteration numbers for optimal step-length and fixed step-length; (b) Relationship between optimal iteration step-length and iteration numbers. |
|
图 2 向下延拓15倍点距 (a)最优步长和固定步长下的误差随迭代次数变化的关系;(b)最优迭代步长和迭代次数的关系. Fig. 2 Downward continuation 15 grid interval (a) Relationship between errors and iteration numbers for optimal step-length and fixed step-length; (b) Relationship between optimal deration step-length and deration numbers. |
|
图 3 向下延拓20倍点距 (a)最优步长和固定步长下的误差随迭代次数变化的关系;(b)最优迭代步长和迭代次数的关系. Fig. 3 Downward continuation 20 grid interval (a) Relationship between errors and iteration numbers for optimal step-length and fixed step-length;(b) Relationship between optimal deration step-length and iteration numbers. |
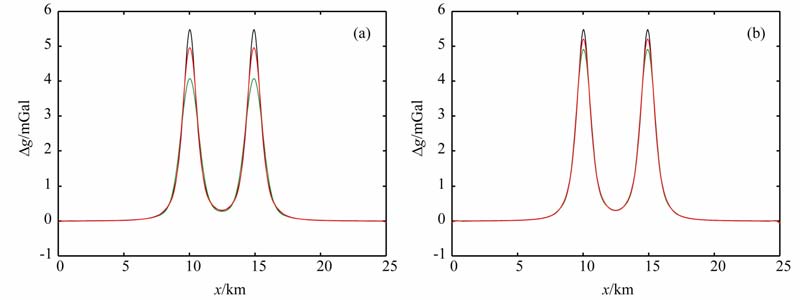
为了延拓效果的直观对比,将用固定步长和最优迭代步长积分迭代法向下延拓1000 m(20 倍点距),将得到的延拓数据与h=1000 m 平面上真实数据在两球心上方主剖面上的值放到一起,其对比如图 4a和图 4b所示.从结果对比可以清晰地看出,在较小迭代次数的情况下,最优迭代步长积分迭代法的延拓结果要明显优于固定步长积分迭代法,换句话说,在相同精度要求条件下,最优迭代步长积分迭代法其要求的迭代次数要远远小于固定步长的积分迭代法.
|
图 4 模型重力数据向下延拓效果在主剖面的对比 (a)各迭代20次;(b)各迭代100次.黑线为原始数据,绿线为固定步长积分迭代法延拓结果,红线为最优迭代步长积分迭代法延拓结果 Fig. 4 Effect comparison of downward continuation to modll gravity data on the main profile (a) Iteration 20 times each other; (b) Iteration 100 times each other.Black line for original data,green line for downward continued data using the fixed step-length integral iteration method, red line for downward continued data using the optimal step-length integral iteration method. |
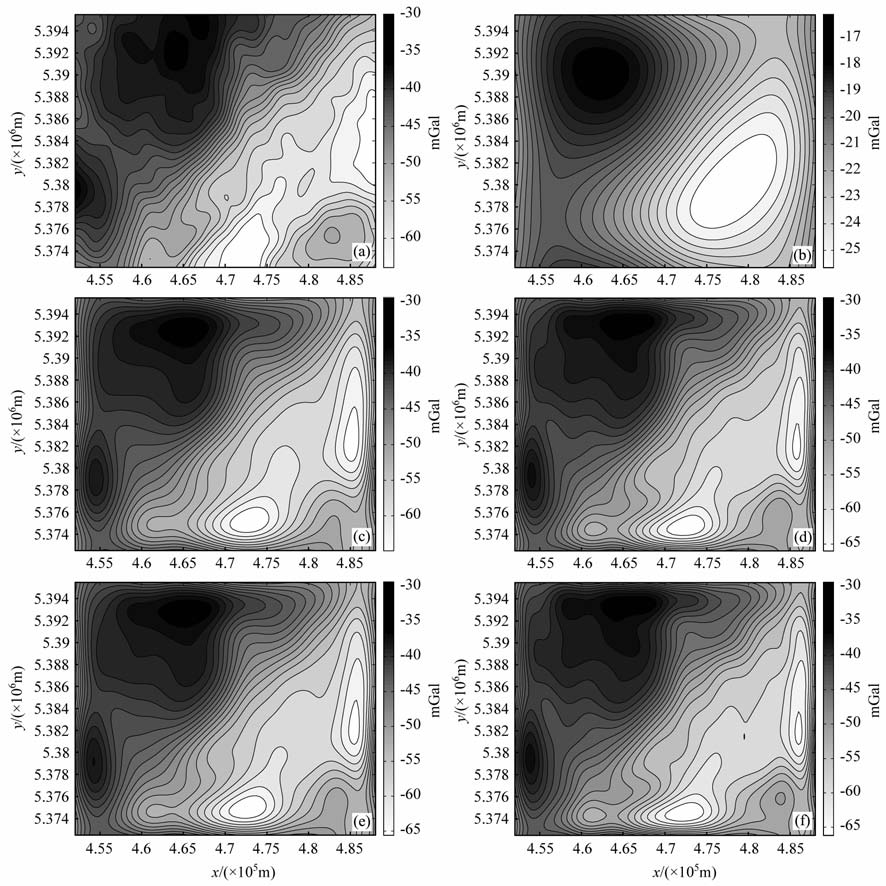
实测数据采用SGL公司在加拿大南部边界渥太华地区测量的布格重力异常数据[22].该次测量在WGS84UTM 坐标下的实际测区范围为东西方向:452000~488000m, 南北方向:5372500~5395500m, 地形平均海拔高度268m, 航测飞机飞行高度约468m.原始数据网格化后点距和线距均为250 m, 其等值线图见图 5a;将原始数据向上延拓5000m(20倍点距)后,结果见图 5b;将向上延拓5000 m 后的布格重力异常数据分别采用固定步长为1的积分迭代法和最优步长积分迭代法向下延拓回原来的高度,其中,迭代100次后其结果分别如图 5c和5d所示,迭代200次后其结果分别如图 5e和5f所示.
|
图 5 实测数据向下延拓效果对比 (a)原始重力异常等值线图;(b)向上延拓20倍点距;(c)固定积分迭代法迭代100次向下延拓20倍点距;(d)最优迭代步长积分迭代法迭代100 次向下延拓20倍点距;(e)固定积分迭代法迭代200次向下延拓20倍点距;f最优迭代步长积分迭代法迭代200次向下延拓20倍点距. Fig. 5 Effects comparison of downward continuation based on the real data (a) Contours of the original gravity anomaly data; (b) Upward continuation 20 grid interval; (c) Iteration 100 times and downward continuation 20 grid interval by the fixed step-length integral iteration method; (d)tteration 100 times and downward continuation 20 grid interval by the optimal step-length integral iteration method; (e) Iteration 200 times and downward continuation 20 grid rnterval by the fixed step-length mtegral deration method; (d)Iteration 200 tmes and downward continuation 20 grid mterval by the optimal step-length rntegral deration method. |
将图 5c~5f与图 5a进行比较可见,图 5d和图 5f的延拓效果要优于图 5c和图 5e,特别是在一些极值点上,最优迭代步长积分迭代法的延拓效果优势明显.
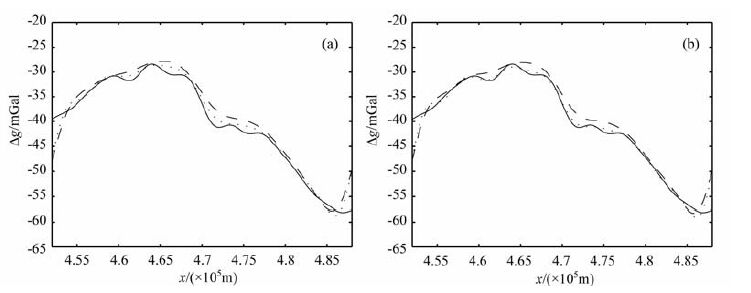
图 6a是按公式(18)计算得到的两种方法的延拓误差随迭代次数变化的对比图;图 6b是最优迭代步长随迭代次数的变化过程.同样,为了对比明显,给出了东西方向一条过坐标为5392250 m 的测线剖面图,其中,实线是真实值,虚线是固定步长积分迭代法延拓结果,点线是最优迭代步长积分迭代法延拓结果,由图 7可见:(1)最优迭代步长积分迭代法相对固定步长为1的积分迭代法具有很小的初始延拓误差,如迭代1次,前者的延拓误差为5.2939mGal, 而后者的延拓误差为15.8852mGal(对比图 6a),且随着迭代次数的增加,前者的延拓误差始终要小于后者的延拓误差;(2)最优迭代步长前期有震荡,迭代一定次数后基本保持不变(图 6b);(3)最优步长积分迭代法的延拓结果与原始重力异常数据更加吻合(对比图 7(a, b)).

|
图 6 向下延拓20倍点距 (a)最优步长和固定步长下的误差随迭代次数变化的关系;(b)最优迭代步长和迭代次数的关系. Fig. 6 Downward continuation 20 grid interval (a) Relationship between errors and iteration numbers for optimal step-length and fixed step-length; (b) Relationship between optimal iteration step-length and iteration numbers;(c) Comparison on the main profile after iteration 20 times each other. |
|
图 7 实测重力异常数据向下延拓效果在剖面的对比 (实线为原始数据,虚线为固定步长积分迭代法延拓结果,点线为最优迭代步长积分迭代法延拓结果)(a)迭代100次的剖面对比;(b)迭代200次的剖面对比. Fig. 7 Effect comparison of downward continuation to the tested real gravity anomaly data on the profile (solid lines for original data, dashed lines for downward continued data using the fixed step-length integral iteration method, dotted lines line for downward continued data using the optimal step-length rntegral deration method).(a) Comparison on the profile after deration 100 tmes each other; (b) Comparison on the profile after deration 200 tmes each other. |
(1) 位场向下延拓的积分迭代法是徐世浙院士基于位场延拓的物理意义提出的.本文针对其迭代式,利用Kirsch正则化子理论和数学归纳法,分析了积分迭代法的正则性,并由其正则化滤子函数证明该迭代法是一种求解不适定反问题的正则化方法,从而将积分迭代法归类到正则化方法,并将有利于将该迭代法推广到其它领域的反问题求解.
(2) 通过计算积分迭代法迭代过程中的最优迭代步长,得到了基于最优迭代步长的积分迭代法,理论模型数据和实测数据延拓结果对比表明,最优迭代步长积分迭代法相对固定步长积分迭代法具有较小的延拓误差,特别是具有相对很小的初始延拓误差.
| [1] | Rice H, Kelmenson S, Mendelsohn L. Geophysical navigation technologies and applications. Position Location and Navigation Symposium, IEEE PLANS , 2004: 618-624. |
| [2] | 许大欣. 利用重力异常匹配技术实现潜艇导航. 地球物理学报 , 2005, 48(4): 812–816. Xu D X. Using gravity anomaly matching techniques to implement submarine navigation. Chinese J. Geophys (in Chinese) , 2005, 48(4): 812-816. |
| [3] | 郭才发, 胡正东, 张士峰, 等. 地磁导航综述. 宇航学报 , 2009, 30(4): 1314–1319. Guo C F, Hu Z D, Zang S F. A Survey of Geomagnetic Navigation. Journal of Astronautics (in Chinese) (in Chinese) , 2009, 30(4): 1314-1319. |
| [4] | 徐世浙. 位场延拓的积分-迭代法. 地球物理学报 , 2006, 49(4): 1176–1182. Xu S Z. The integral-iteration method for continuation of potential field. Chinese J. Geophys (in Chinese) , 2006, 49(4): 1176-1182. |
| [5] | Xu S Z, Yang J Y, Yang C F, et al. The iteration method for downward continuation of a potential field from a horizontal plane. Geophsical Prospecting , 2007, 55: 883-889. DOI:10.1111/gpr.2007.55.issue-6 |
| [6] | 王顺杰, 朱海, 栾禄雨. 水下地磁导航中位场积分迭代法收敛性分析. 地球物理学进展 , 209, 24(3): 1095–1097. Wang S J, Zhu H, Luan L Y. Constringency analysis of the iteration method for continuation of potential fields in underwater geomagnetism navigation. Progress in Geophys (in Chinese) , 209, 24(3): 1095-1097. |
| [7] | 张辉, 陈龙伟, 任治新, 等. 位场向下延拓迭代法收敛性分析及稳健向下延拓方法研究. 地球物理学报 , 2009, 52(4): 1107–1113. Zhang H, Chen L W, Ren Z X, et al. Analysis on convergence of iteration method for potential fields downward continuation and research on robust downward continuation method. Chinese J. Geophys (in Chinese) , 2009, 52(4): 1107-1113. |
| [8] | 刘东甲, 洪天求, 贾志海, 等. 位场向下延拓的波数域迭代法及其收敛性. 地球物理学报 , 2009, 52(6): 1599–1605. Liu D J, Hong T Q, Jia Z H, et al. Wave number domain iteration method for downward of potential fields and its convergence. Chinese J. Geophys (in Chinese) , 2009, 52(6): 1599-1605. |
| [9] | 于波, 翟国君, 刘雁春, 等. 噪声对向下延拓迭代法的计算误差影响分析. 地球物理学报 , 2009, 52(8): 2182–2188. Yu B, Zhai G J, Liu Y C, et al. Analysis of noise effect on the calculation error of downward continuation with iteration method. Chinese J. Geophys (in Chinese) , 2009, 52(8): 2182-2188. |
| [10] | Tikhonov A N, Arsenin N Y. Solutions of Ill-Posed Problems. New York: Wiley, 1977 . |
| [11] | 肖庭延, 于慎根, 王彦飞. 反问题的数值解法. 北京: 科学出版社, 2003 . Xiao T Y, Yu S G, Wang Y F. Numerical Methods for the Solution of inverse Problems (in Chinese) (in Chinese). Beijing: Science Press, 2003 . |
| [12] | 安玉林, 管志宁. 滤除高频干扰的正则化稳定因子. 物化探计算技术 , 1985, 7(1): 13–23. An Y L, Guan Z N. A regularized stable operator for filtering high frequency interference. Computing Techniques for Geophysical and Geochemical Exploration (in Chinese) (in Chinese) , 1985, 7(1): 13-23. |
| [13] | 梁锦文. 位场向下延拓的正则化方法. 地球物理学报 , 1989, 32(5): 600–608. Liang J W. The regularization method for downward continuation of Potential field. Chinese J. Geophys (in Chinese) , 1989, 32(5): 600-608. |
| [14] | Cooper G. The stable downward continuation of potential field data. Exploration Geophysics , 2004, 35(2): 260-265. |
| [15] | 王兴涛, 石磐. 航空重力测量数据向下延拓的正则化算法及谱分析. 测绘学报 , 2004, 33(1): 33–38. Wang X T, Shi P. Regularization methods and spectral decomposition for the downward continuation of airborne gravity data. Acta Geodaetica et Cartographica Sinica (in Chinese) (in Chinese) , 2004, 33(1): 33-38. |
| [16] | 王兴涛, 夏哲仁, 石磐, 等. 航空重力测量数据向下延拓方法比较. 地球物理学报 , 2004, 47(6): 1017–1022. Wang X T, Xia Z R, Shi P. A comparison of different downward continuation methods for airborne gravity data. Chinese J. Geophys. (in Chinese) , 2004, 47(6): 1017-1022. |
| [17] | 陈龙伟, 张辉, 郑志强, 等. 水下地磁辅助导航中的地磁场延拓方法. 中国惯性技术学报 , 2007, 15(6): 693–697. Chen L W, Zhang H, Zheng Z Q, et al. Technique of geomagnetic field continuation in underwater geomagnetic aided navigation. Journal of Chinese Inertial Technology (in Chinese) , 2007, 15(6): 693-697. |
| [18] | 郝燕玲, 成怡, 孙枫, 等. Tikhonov正则化向下延拓算法仿真实验研究. 仪器仪表学报 , 2008, 29(3): 605–609. Hao Y L, Cheng Y, Sun F, et al. Simulation research on Tikhonov regularation algorithm in downward continuation. Chinese Journal of Scientific Instrument (in Chinese) (in Chinese) , 2008, 29(3): 605-609. |
| [19] | Kirsch A. An introduction to the mathematical theory of inverse problems. New York: Springer, 1996 . |
| [20] | 管志宁. 地磁场与磁力勘探. 北京: 地质出版社, 2005 . Guan Z L. Geomagnetic Field and Magnetic Exploration(in Chinese) (in Chinese). Beijing: Geological Publishing House, 2005 . |
| [21] | 陈生昌, 肖鹏飞. 位场向下延拓的波数域广义逆算法. 地球物理学报 , 2007, 50(6): 1816–1822. Chen S C, Xiao P F. Wavenumber domain generalize inverse algorithm for potential field downward continuation. Chinese J. Geophys. (in Chinese) , 2007, 50(6): 1816-1822. |
| [22] | Elieff S, M Sc. Project report for an airborne gravity evaluation survey, Timmins, Ontario: Report produced for Timmins Economic Development Corp. on behalf of the Discover Abitibi Initiative. 2003.7〈http://www.discoverabitibi.com/technical-projects.htm〉 |
 2011, Vol. 54
2011, Vol. 54


