随着我国油气勘探向西部和西南部的转移,复杂地表及复杂构造问题变得非常突出,地震资料信噪比低、地震成像困难等问题严重影响着这些地区的勘探效果.搞清楚地震波在复杂地质条件下的传播规律与能量分布特征对地震数据采集、处理和解释具有重要意义.
地震波照明分析是一种对地下地震波传播特征和能量分布进行定量分析的技术[1, 2].一般地,地震波照明可以分为基于射线追踪的地震波照明方法和基于波动方程的地震波照明方法两类.射线追踪地震波照明方法目前应用最为普遍[3~7],该方法简单直观、计算效率高,但由于射线理论本身的缺陷(如高频近似、射线盲区等)和复杂介质中的奇异性问题,基于射线的照明分析方法在复杂构造区会出现很大的误差,照明精度较低[7].而基于波动方程的地震波照明方法能有效地克服射线照明分析方法在复杂构造区的不足,尤其是利用波动方程中的单程波方程的地下照明分析是近几年的一个研究热点.它克服了射线照明方法的缺陷,能适应强横向变速介质,使得目标照明分析更加合理、准确[8],同时波动方程的照明分析结果还可用于进行偏移成像结果的振幅校正[9~11].将单程波传播算子与局部平面波分解算子或其他分解算子(如余弦分解、小波变换分解)相结合,可以实现平面波源或小束源地震波定向照明分析和成像振幅校正[12~15].
如果将“波的激发与接收"作为地震波照明计算时的一个考虑因素,则地震波照明分析又可分为单向照明与双向照明.单向照明是指仅考虑震源激发的地震波在地下介质中传播时的能量分布,通常的地震波照明是指单向照明,也称源照明.Wu等将地震观测系统中震源激发的地震波在地下传播过程中的能量分布作为地下照明的量度,是一种基于波动方程的单向照明分析方法[8~15].
如果在源照明基础上,考虑检波器排列的接收效应,这种地震波照明则称为双向照明,也称源-检照明.对于地下某一目标的最佳照明源和最佳采集数据,即是采集系统的源激发的入射波,在上覆复杂构造介质中传播后,垂直照明在目标结构反射面上,且照明强度高而均匀,这种照明的入射波被目标反射,经过上覆介质再次传播后,最多的反射能量能够被观测系统的接收器所接收[11].如果震源波场对某一地下目标照明后,由目标体反射回地面的能量未能被检波器接收到,则无论源照明能量多强多均匀,地面接收到的信号中都没有来自该目标体的反射信息,后续处理方法无论多么精准也无法得到该目标体的相关信息.可以用一个形象的例子来说明这个道理:在黑暗中手电筒照亮了一个物体,视力好的人可以看到该物体是因为照亮的物体的反射光能够被他检测到;但即使手电筒对该物体照射得很亮,一个盲人也无法看到该物体,那是因为照亮物体的反射光无法被他接收到.从这个意义上说,考虑检波器效应的双向照明相比单向照明更具有实际意义.
虽然双向照明的物理意义很明确,但如何合理计算双向照明度到目前为止尚未得到很好的解决.Berkhout等基于共聚焦点(Common Focus Point, CFP)的概念把地下的双聚焦点视为照明分析点,利用双聚焦(检波器聚焦和震源聚焦)技术进行照明分析[2].这种方法虽然同时考虑了观测系统中的震源和检波器,但本质上为一种射线方法,在复杂构造区精度有限.Xiao-BiXie、陈生昌等基于震源与检波器之间的互易关系,同时从观测系统中的震源位置和检波器位置激发地震波来计算地下介质中的双向照明值[16, 17],并将这种方法称为波动方程双程地下方向照明分析方法.LiWan-wan指出该方法是地震偏移成像的另一种表征形式[18],与偏移成像之间存在映射关系.由于该方法是由Xie和Wu提出,本文中我们称之为Xie双向照明方法.
Xie和Wu提出的双向照明计算方法是将震源延拓波场与检波器延拓波场相关求能量作为双向照明强度.实际应用中,由于在每炮每个检波器处都要进行一次波场延拓,所以该方法的计算效率较低.此外,虽然在源照明基础上增加考虑了介质中接收点处的波场因素,但该方法中震源与检波器处的初始波场均为同一地震子波,这便有可能导致得到的双向照明结果不能明确体现出“不同位置处的检波器所接收到的反射波场不尽相同"这一客观问题.
从双向照明的物理意义出发,我们给出了双向照明的基本概念,并根据该定义提出了一种双向照明计算思路(文中称为DUC 双向照明方法).为了提高DUC 双向照明计算效率,提出了DUC-DC 双向照明计算方法,最后进行了几种双向照明方法的数值试验,从计算精度和计算效率上对几种方法进行了对比.
2 方法原理 2.1 双向照明的概念根据WRW 波场传播理论,震源激发的地震波引起地下某一点的振动,该点以这个振动为“二次震源子波"再次“激发"地震波传播至各检波器.因此,地下某一介质点(即使该点不会产生反射波)的地震波双向照明强度应该理解为震源激发的地震波引起该点振动,由该振动引起的反射地震波再次传播至各检波器所接收到的地震波总能量.
实际中,地下某一介质点并不一定是反射点,但这里如果考虑反射系数,当一个点不产生反射波时,这个点的双向照明强度就为零!这样考虑双向照明显然是没有意义的.实际中无论是地震数据采集还是处理解释,在应用双向照明时均可假定为地下一点的振动向外传播至检波器所接收到的能量.而且,地震波照明分析主要是为了得到地震波在地下介质中的宏观能量强弱分布趋势,因此,我们假定地下介质在被震源照明后,能量全部被“反射"回来,不对地下介质的反射系数进行细致考虑,主要讨论在某一炮检布设关系下,地震波能量在地下介质中的宏观分布情况.
2.2 DUC双向照明计算方法根据上文提出的双向照明概念,下面讨论双向照明的计算方法.
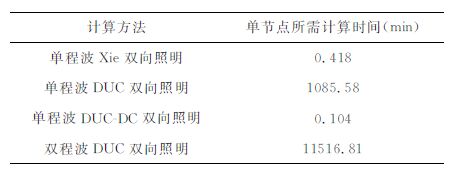
我们认为,在xs处的震源激发的地震波引起地下任意一点(x,z)的振动u(xs;x,z,t)(在频率域表示为U(xs;x,z,ω)),该振动再次激发地震波向外传播,检波器xg接收到的地震波场为u(xs,xg;x,z,t)(在频率域表示为U(xs,xg;x,z,ω)).这样,震源xs激发、检波器xg接收的地震波在地下(x,z)点的双向照明强度就可以定义为
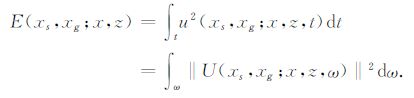
|
(1) |
同理,单个震源xs激发、Ng个检波器接收的单炮地震波在地下(x,z)点的双向照明强度为
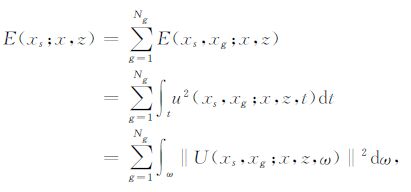
|
(2) |
则Ns个震源激发、每炮Ng个检波器接收的观测系统对地下(x,z)点的双向照明强度可表达为

|
(3) |
按照以上给出的地震波双向照明的概念和计算思路,在计算一个震源点激发、一个检波器接收时的地下任一点的双向照明强度时,需要进行一次震源波场延拓和一次“反射"波场延拓,因此,我们将其命名为Downand UpComing(DUC)双向照明分析思路.
实际上该双向照明思路与著名的WRW 模型是一致的.(3)式积分将各检波点实际接收到的来自地下某一“反射点"的能量累加起来,得到在地下(x,z)点的双向照明强度.整个计算过程中,将震源激发波场在地下介质中的下行传播效应、经“反射点"“反射"产生的“反射波场"传播效应以及采集系统接收点的接收效应都概括在计算中,具有非常明确的物理含义.
具体的双向照明计算方法,则完全取决于震源xs激发引起的地下点(x,z)的振动u(xs;x,z,t)(在频率域表示为U(xs;x,z,ω))以及该振动激发的地震波场向外传播至检波器xg接收到的地震波场u(xs,xg;x,z,t)(在频率域表示为U(xs,xg;x,z,ω))的计算方法,用不同的方法计算这两个波场分布,就产生了不同的地震波双向照明计算方法.
例如,如果利用双程波方程通过模拟计算这两个波场,则产生了双程波方程DUC 双向照明方法(简称双程波DUC 双向照明).如果利用单程波方程进行深度延拓计算这两个波场,则产生了单程波方程DUC 双向照明方法.在没有特别指明的情况下,后面的DUC 双向照明均是指单程波方程DUC双向照明.
2.3 DUC 双向照明的计算效率尽管从双向照明概念上讲,DUC 双向照明方法的物理解释较为明确,但该方法的实现需要对地下每个点单独计算其双向照明值,计算量非常庞大.
对于介质参数为NX×NZ的2D 模型,若总炮数为Ns,每炮检波器个数为Ng,频率个数为Nω,则完成该2D 模型的单程波DUC 双向照明度计算,需要进行
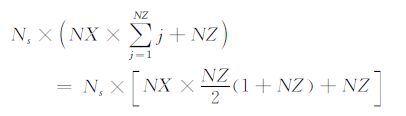
|
次波场延拓计算.每次延拓计算中需要进行Nω 次频率循环,统计计算地下每个点的照明强度共需要Ns×Ng次加法计算.显而易见,该方法的致命缺陷是庞大的计算量.
如果改用双程波DUC 双向照明方法,则完成上述2D 模型的双向照明度计算需要进行Ns×2×(NX×NZ)次波场模拟.双程波DUC 双向照明方法尽管更精确,但比单程波DUC 双向照明的计算效率更低.
2.4 提高DUC双向照明计算效率的DUC-DC双向照明计算方法为了提高DUC 双向照明方法的计算效率,本文在双向照明的概念及理论分析的基础上,借鉴地震波模拟和地震偏移中波场反向外推的思想,对DUC 双向照明方法进行改进,以提高计算效率,并将改进后的DUC 双向照明方法称为DUC-DC 双向照明方法.
与DUC 双向照明方法一致,DUC-DC 双向照明方法在具体实现过程中可以根据所采用的波场延拓算子分为单程波DUC-DC 双向照明方法和双程波DUC-DC 双向照明方法.这里,我们采用频率空间域单程波波场延拓算子来说明DUC-DC 双向照明方法原理.
入射波在某一深度层的波场分布是将震源波场向下延拓至该深度的结果S(xs;x,z,ω)= S(xs,ω)·H(z),式中,H(z)是延拓算子.
第一步,首先将震源函数S(xs,ω)沿深度方向延拓,记录下每个深度层的延拓波场S(xs;x,z,ω).当延拓至最底层后,将波场从底层开始反向延拓,得到各个检波器xg记录到的来自地下各点的地震波场U(xs,xg;ω).该波场可以看作是震源xs激发的地震波场经地下各点“反射"后传至各检波点xg处的波场.这一步,实际上是在假定地下各点均产生“反射波场"的情况下(这与双向照明的概念是一致的),计算得到了当前炮激发时对应的各检波器接收到的地震记录.
第二步,将地面各个检波器接收到的反射信号U(xs,xg;ω)作为合成震源Usyn∣ g=g1,gn(xs,ω),沿深度方向再次延拓至地下各个深度层,得到地下各点的波场值:
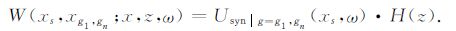
|
(4) |
这一步,类似于地震偏移中对记录波场的反向传播,是通过该炮各检波器接收到的地震记录来反向预测地下各点的波场分布,实际上为一个能量再分配的过程.由于地表各检波器接收到的信号受到地下所有介质点的综合影响,需要将地表接收到的记录再次延拓至地下各深度层后取能量值作为双向照明强度分布,其物理意义也是比较明确的.
这样,炮点在xs,检波器分别在xg1,xg2,…,xgn处的观测系统在地下各点的双向照明度可以表示为
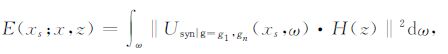
|
(5) |
因此,Ns炮的整个观测系统在地下各点的双向照明度为
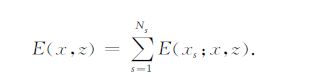
|
(6) |
以地下任一介质点为参照,按照上面的思路进行双向照明计算需要进行三次波场延拓:一次震源波场延拓、一次反射波场延拓和一次由各检波器接收的地震记录作为合成震源的延拓,也就是在DUC双向照明方法的基础上增加了由各检波器接收的地震记录作为合成震源的波场延拓这一步,这也就是我们将该方法命名为DUC-DC(Down and Up Coming-Down Coming)双向照明方法的原因.
2.5 DUC-DC双向照明方法的计算效率
对于介质参数为NX×NZ的2D 模型,若总炮数为Ns,每炮检波器个数为Ng,频率个数为Nω,则完成该2D 模型的单程波DUC-DC 双向照明度计算所需要的计算量为:3×Ns×NZ次波场延拓计算,每次延拓计算中需要进行Nω 次频率循环.与单程波DUC 双向照明方法相比,计算效率提高了m=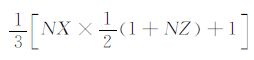
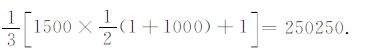
如果采用双程波DUC-DC 双向照明方法,则完成上述2D 模型的双向照明度计算需要进行Ns×3次波场模拟.与双程波DUC 双向照明计算方法相比,计算效率提高了m=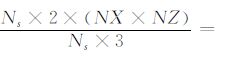
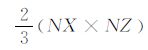
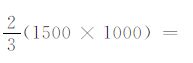
显然,无论是用单程波方程还是双程波方程,改进后的DUC-DC 双向照明方法可以大幅度提高计算效率.
3 数值试验在本文的数值实验过程中,主要采用单程波算子进行波场延拓计算.为便于对比分析,根据均匀介质中地震波振幅随传播距离增大而扩散衰减的解析表达式计算出均匀介质中的理论双向照明强度分布,以此作为准确值,对几种双向照明方法(分别简写为Xie、DUC、DUC-DC 双向照明方法)的实验结果进行比较.对于非均匀介质模型,由于没有解析解,鉴于DUC 思路下的双程波延拓双向照明方法的准确性,我们可以将其作为参照,比较三种单程波方程双向照明计算方法的精度.
3.1 均匀介质模型试验与计算效率分析首先是基于2D 均匀介质模型进行几种双向照明方法数值试验.图 1是理论双向照明计算方法、双程波DUC 双向照明方法、单程波Xie双向照明方法、单程波DUC 双向照明方法和单程波DUC-DC双向照明方法得到的双向照明计算结果.观测系统为中间放炮,双边各5 道接收,道距160 m, 炮点位于模型中间1km 位置处.
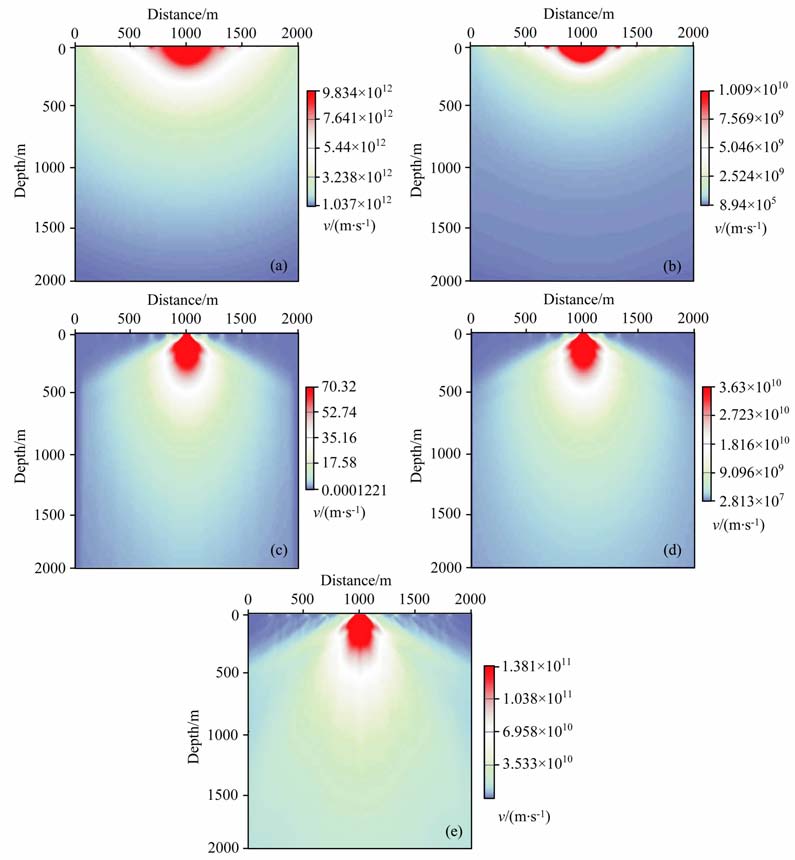
|
图 1 均勻介质情况下不同方法的双向照明结果 (a)理论计算;(b)双程波DUC双向照明;(c)单程波Xie双向照明;(d)单程波DUC双向照明;(e)单程波DUC-DC双向照明. Fig. 1 Bi-directional illumination results in homogeneous medium (a) In theory; (b) DUC double-way wave-equation-based; (c) Xie one-way wave-equation-based;(d) DUC one-way wave-equation-based; (e) DUC-DC one-way wave-equation-based. |
从照明结果可以直观看出,双程波DUC 双向照明结果(图 1b)与均匀介质中理论双向照明结果(图 1a)非常接近,这说明了双程波DUC 双向照明方法的可靠性.
我们按照图 2所示的截取曲线方式,以震源为圆心,对上述各种照明结果抽取某一半径圆周上的照明能量曲线,深入对比分析几种双向照明方法.图 3是半径为400m 时,能量随角度θ 的变化曲线.
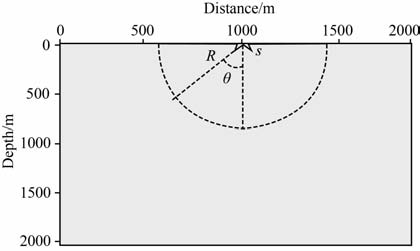
|
图 2 精度对比截取曲线示意图 (s为震源R为圆周半径,$\theta $为角度) Fig. 2 Curve configuration for accuracy comparison in Fig. 3 (s represents the source,R represents the radius and $\theta $ represents the angle) |
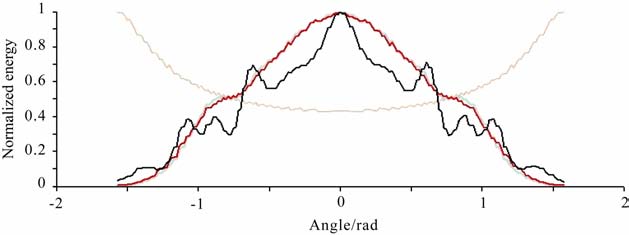
|
图 3 几种双向照明方法圆周曲线对比(圆周半径R= 400 m,均勻介质) 黄色:理论计算;浅绿色:DUC双程波双向照明;红色:Xie单程波双向照明;淡蓝色:DUC单程波双向照明;墨绿色:DUC-DC单程波双向照明. Fig. 3 Computational accuracy comparison for tive bi-directional tllumination methods tn Fig. 1 (radius = 400 m) Yellow: In theory; Light green: DUC double-way wave-equation-based; red: Xie one-way wave-equation-based; light blue: DUC one-way wave-equation-based; green black: DUC-DC one-way wave-equation-based. |
可以看出,均匀介质中,双程波DUC 双向照明曲线与理论双向照明曲线几乎完全重合,其精度是最高的(理论曲线与双程波曲线的振荡是由于模型离散使得所取点的位置并不正好在圆周上所致),这就说明了DUC 双向照明度计算方法的正确性,并证明了本文提出的双向照明概念的正确性.三种单程波双向照明曲线在大角度时与理论曲线的差异主要是源于单程波算子的角度近似.三种单程波双向照明方法中,DUC 双向照明方法与Xie双向照明方法的实验结果较为相近;而DUC-DC 双向照明结果中,在设有检波器的对应位置处,能量曲线出现明显振荡.
从计算效率上来看,对于均匀介质模型(NX×NZ=201×201,DX×DZ=10m×10m, 速度4000m/s),采用中间放炮两边各5 道检波器对称接收,检波器间距160m, 最大偏移距800m.单炮覆盖水平长度1600m, 延拓深度为2000 m.单节点计算一炮的双向照明所需要的计算时间见表 1.可以看出,单程波DUC-DC 双向照明方法计算效率是最高的,相对单程波Xie双向照明方法、单程波DUC 双向照明方法、双程波DUC 双向照明方法,在效率上分别提高了4倍、6600倍、160000 倍.可见,提出的DUC-DC单程波双向照明方法具有很高的计算效率.
|
|
表 1 不同双向照明方法计算效率比较(均匀介质) Table 1 Comparisons of computational time for four solutions (homogeneous medium) |
我们采用如图 4所示的2D 断块模型再次进行双向照明方法的数值试验.
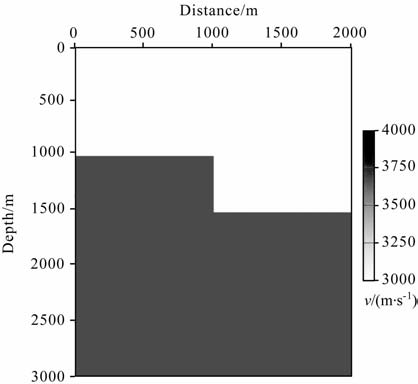
|
图 4 二维断块模型 Fig. 4 2D numerical model 1 |
设定观测系统与均匀介质模型试验中一致,得到双程波DUC 双向照明结果、单程波Xie双向照明结果、单程波DUC 双向照明结果与单程波DUC-DC 双向照明结果,如图 5所示.
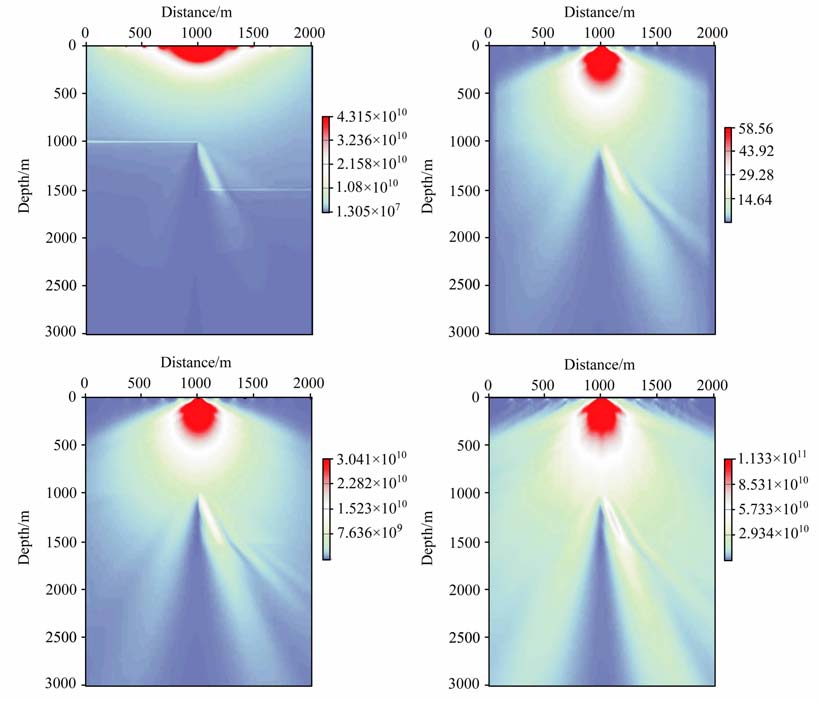
|
图 5 二维断块模型四种方法双向照明结果 (a)双程波DUC双向照明;(b)单程波Xie双向照明;(c)单程波DUC双向照明;(d)单程波DUC-DC双向照明. Fig. 5 Bi-directional illumination results for 2D numerical model in Fig. 4 (a) DUC double-way wave-equation-based; (b) Xie one-way wave-equation-based;(c) DUC one-way wave-equation-based; (d) DUC-DC one-way wave-equation-based. |
与均匀介质数值试验中一样,基于上述照明结果,我们抽取以震源为圆心的照明能量圆周曲线对几种双向照明方法进行比较.图 6为半径600 m 时的照明能量圆周曲线.

|
图 6 几种双向照明方法圆周曲线对比(圆周半径R= 600 m,断块模型) 黄色:DUC双程波双向照明;红色:Xie单程波双向照明;淡蓝色:DUC单程波双向照明;墨绿色:DUC-DC单程波双向照明. Fig. 6 Computational accuracy comparison for four bi-directional tlumination methods nFig. 5 (radius = 600 m) Yellow:DUC double-way wave-equation-based;red: Xie one-way wave-equation-based; light blue: DUC one-way wave-equation-based; green black: DUC-DC one-way wave-equation-based. |
可以发现,对于图 4所示的模型,单程波DUC-DC 双向照明圆周曲线与单程波DUC 双向照明圆周曲线、单程波Xie双向照明圆周曲线比较接近.
从计算效率上来看,对于上述断块模型(NX×NZ=201×301,DX×DZ=10m×10m, 最大速度4000m/s),采用中间放炮两边各5道检波器对称接收,检波器间距160 m, 最大偏移距800 m.单炮覆盖水平长度1600m, 延拓深度为2000m.单节点计算一炮的双向照明所需要的计算时间见表 2.
|
|
表 2 不同双向照明方法计算效率比较(断块模型) Table 2 Comparisons of computational time for four solutions (2D numerical model 1) |
可以看出,在相同的观测系统参数下,采用单程波DUC-DC 双向照明方法的计算效率约是单程波Xie双向照明方法的4倍.因此,单程波DUC-DC 双向照明方法可以有效提高双向照明度计算的效率,较其余两种方法都有优势.
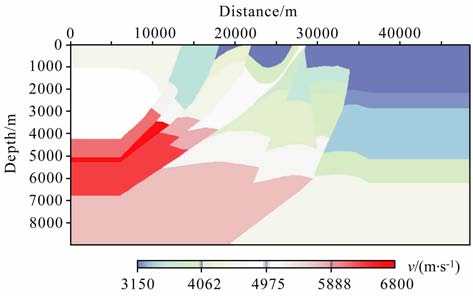
3.3 复杂模型试验选用图 7所示的水平地表逆掩推覆模型,对单程波Xie双向照明方法与单程波DUC-DC 双向照明方法进行数值试验与比较.设定观测系统为中间放炮,各炮设置9 个检波器,两边对称接收,检波器间距为2km, 即两边排列长度均为8km.图 8和图 9分别展示了震源位于18km 和23km 时单程波Xie双向照明方法和单程波DUC-DC 双向照明方法得到的双向照明结果.图 10为炮点全覆盖时使用单程波DUC-DC 双向照明方法得到的照明结果(第一炮位于图 7中横向8km 位置处,炮间距为20m, 共1600炮).
|
图 7 二维水平地表逆掩推覆构造模型 Fig. 7 2D numerical model 2 |
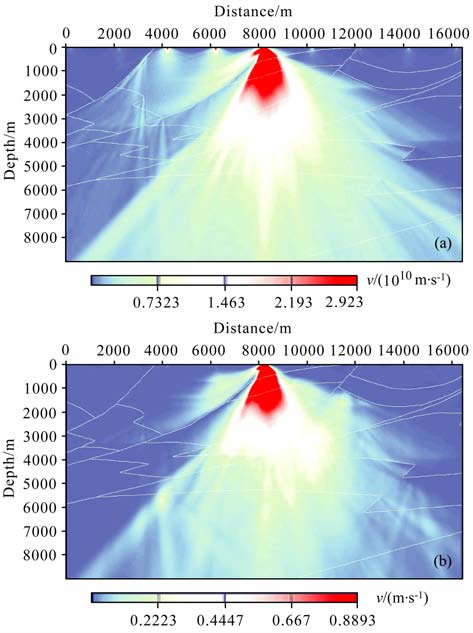
|
图 8 炮点在18 km处的单炮双向照明结果 (a)单程波DUC-DC双向照明;(b)单程波Xie双向照明. Fig. 8 Bi-directional illumination result of a single shot in 18 km (a) DUC-DC one-way wave-equation-based;(b) Xie one-way wave-equation-based. |

|
图 9 炮点在23 km处的单炮双向照明结果 (a)单程波DUC-DC双向照明;(b)单程波Xie双向照明. Fig. 9 Bi-directional illumination resutt of a single shot in 23 km (a) DUC-DC one-way wave-equation-based;(b) Xie one-way wave-equation-based. |
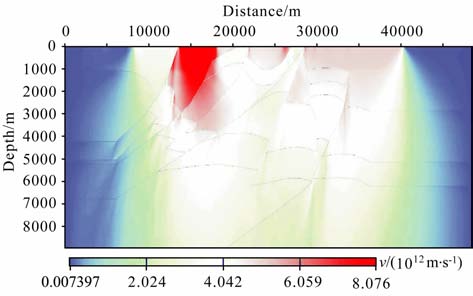
|
图 10 多炮单程波DUC-DC双向照明结果 Fig. 10 Bi-directional illumination resutt of multi-shots (DUC-DC one-way wave-equation-based) |
从图 8和9中可以对比发现:单程波Xie双向照明方法与DUC-DC 双向照明方法计算得到的地下双向照明结果在模型深部的宏观分布形态还是比较一致.但在DUC-DC 双向照明结果中,不同位置检波器处的照明能量强弱分布不同体现得更加明显,这主要是由于DUC-DC 双向照明方法考虑了地表不同位置检波器接收能量不同这一因素.这样进行双向照明分析计算,一定程度上可以反映出地表哪些位置更有利于接收,应该更加有利于指导地面检波器布设范围的确定.
4 结论与讨论双向照明在一般源照明基础上增加考虑了介质对地震波能量的反向传播过程,同时将实际观测系统中检波器接收效应和接收孔径等因素纳入考虑范围,计算得到的地下介质中地震波能量分布结果对指导面向目标的地震勘探观测系统设计更加具有实际意义.
本文在分析双向照明的物理概念基础上,提出了基于双程波方程或单程波方程计算双向照明的DUC 双向照明方法,同时提出了提高DUC 双向照明计算效率的DUC-DC 双向照明计算方法,并与较早的一种双向照明方法(Xie双向照明方法)从计算精度和计算效率上进行了比较.
数值试验结果表明,双程波DUC 双向照明方法精度最高,但效率较低,目前难以应用于实际.三种单程波双向照明方法的计算结果总体宏观分布相差不大,其中,单程波DUC 双向照明方法与单程波Xie双向照明方法计算精度较为接近,单程波DUC-DC 双向照明方法较前两者在计算精度上有所降低,但其在计算效率上具有很大的优势.
需要说明的是,文中在双向照明新方法的讨论中对反射系数进行了假设,这便不可避免地在数值试算过程中引入了误差.同时,为了提高效率而提出的DUC-DC 双向照明方法,其正确性和可行性在上述数值试验中得到了一定程度的验证,但仍需要在以后的工作中从理论背景和数值试验等方面进一步对该方法补充完善.
| [1] | Rietveld W E A, Berkhout A J, Wapenaar C P A. Optimum seismic illumination of hydrocarbon reservoirs. Geophysics , 1992, 57(10): 1334-1345. DOI:10.1190/1.1443200 |
| [2] | Berkhout A J, Ongkiehong L, Volker A W F, et al. Comprehensive assessment of seismic acquisition geometries by focal beams-part I: theoretical considerations. Geophysics , 2001, 66(3): 911. DOI:10.1190/1.1444981 |
| [3] | Bear G, Lu C P, Willen D, et al. The construction of subsurface illumination and amplitude maps via ray tracing. The Leading Edge , 2000, 19(7): 726. DOI:10.1190/1.1438700 |
| [4] | Muerdter D, Ratcliff D. Understanding subsalt illumination through ray-tracing modeling, Part 1: Simple 2-D salt models. The Leading Edge , 2001, 20: 578-594. DOI:10.1190/1.1438998 |
| [5] | Muerdter D, Ratcliff D. Understanding subsalt illumination through ray-tracing modeling, Part 2: Dipping salt bodies, salt peaks, and nonreciprocity of subsalt amplitude response. The Leading Edge , 2001, 20: 688-697. DOI:10.1190/1.1487279 |
| [6] | Muerdter D, Ratcliff D. Understanding subsalt illumination through ray-tracing modeling, Part 3: Salt ridges and furrows, and the impact of acquisition orientation. The Leading Edge , 2001, 20: 688-697. DOI:10.1190/1.1487279 |
| [7] | Hoffmann J. Illumination, resolution, and image quality of PP and PS waves for survey planning. The Leading Edge , 2001, 20(9): 1008. DOI:10.1190/1.1487305 |
| [8] | Wu R S, Chen L. Mapping directional illumination and acquisition-aperture efficacy by beamlet propagators. Expanded Abstracts of 72nd SEG Mtg , 2002: 1352-1355. |
| [9] | Rickett J E. Illumination-based normalization for wave-equation depth migration. Geophysics , 2003, 68(4): 1371. DOI:10.1190/1.1598130 |
| [10] | Wu R S, Luo M Q, Chen S C, et al. Acquisition aperture correction in angle domain and true-amplitude imaging for wave equation migration. Expanded Abstracts of 74th SEG Mtg , 2004: 937-940. |
| [11] | 冯伟. 面向目标的地震波照明分析与偏移成像. 上海: 同济大学海洋与地球科学学院 , 2003. Feng W. Target-oriented seismic wave illumination analysis and migration imaging (in Chinese). Shanghai: School of Marine & Earth Science, Tongji University (in Chinese) , 2003. |
| [12] | Wu R S, Chen L, Xie X B. Directional illumination and acquisition dip-response. Expanded Abstract of 65th Conference and Technical Exhibition, EAGE , 2003: 147. |
| [13] | 冯伟, 王华忠, 吴如山, 等. 面向目标控制照明的合成波源偏移. 石油物探 , 2004, 43(3): 223–228. Feng W, Wang H Z, Wu R S, et al. The migration of synthetic waves for target-oriented controlled illumination. Geophysical Prospecting for Petroleum (in Chinese) (in Chinese) , 2004, 43(3): 223-228. |
| [14] | 冯伟, 吴如山, 马在田. 单向传播子的局部平面波分解以及在定向照明分析和目标特征成像中的应用. 地球物理学进展 , 2007, 22(1): 171–178. Feng W, Wu R S, Ma Z T. Local plane wave decomposition of one-way propagator and the applications to directional illumination analysis and target-structure oriented imaging. Progress in Geophysics (in Chinese) (in Chinese) , 2007, 22(1): 171-178. |
| [15] | 冯伟, 吴如山, 王华忠, 等. 面向目标的小束源照明和成像. 地球物理学进展 , 2006, 21(3): 802–808. Feng W, Wu R S, Wang H Z, et al. Target-oriented beam source illumination and imaging. Progress in Geophysics (in Chinese) (in Chinese) , 2006, 21(3): 802-808. |
| [16] | Xie X B, Jin S W, Wu R S. Wave-equation-based seismic illumination analysis. Geophysics , 2006, 71(5): 169-177. DOI:10.1190/1.2227619 |
| [17] | 陈生昌, 马在田, 吴如山. 波动方程双程地下方向照明分析. 同济大学学报 (自然科学版) , 2007, 35(5): 682–684. Chen S C, Ma Z T, Wu R S. Two-way subsurface directional illumination analysis by wave equation. Journal of Tongji University (Natural Science) (in Chinese) (in Chinese) , 2007, 35(5): 682-684. |
| [18] | Li W W. Design of seismic geometry based on wave equation forward simulation. Oil Geophysical Prospecting , 2008, 43(2): 134-141. |
 2011, Vol. 54
2011, Vol. 54